多阶段电网规划模型与混合优化方法
丘文千, 丘 扬
(1.浙江省电力设计院,杭州 310012;2.杭州市电力局,杭州 310009)
输 配 电
多阶段电网规划模型与混合优化方法
丘文千1, 丘 扬2
(1.浙江省电力设计院,杭州 310012;2.杭州市电力局,杭州 310009)
提出以满足系统可靠性准则为约束条件和系统发展过程中各阶段建设费用为优化目标的电网规划模型,运用混合优化方法求解此优化规划模型,可有效提高收敛性能和稳定性。运用递延枚举优化进行局部深度搜索,即可得到方案的局部最优解。运用分解递延枚举和隐含递延枚举技术加快递延枚举过程。通过算例验证了规划模型及其优化方法的实用性和有效性。
电力系统可靠性;随机规划;不确定规划;多阶段规划;遗传算法
可靠性是衡量电力系统性能的一个重要指标,是电力系统规划设计应遵循的重要技术标准,而提高系统可靠性一般需要投入更多资金。因此,合理的可靠性标准应与社会经济发展水平相适应。为确保电力系统的可靠性在合理的范围内,世界各国电力系统都有相应的可靠性标准或准则,例如对系统发电备用容量的规定、对系统可靠性指标的规定、在系统规划设计中采用的n-1准则等。
电网建设与运行是动态过程,对某一水平年有利的方案未必对整个规划期总体效益有利。因此,不能仅考虑单一负荷水平下电网结构的优化,还应考虑在一定时期发展过程中整个系统的最优性。若以建设投资及运行费用来衡量,最优方案应该是总费用折现值最小的方案。
电网规划本质上是多目标的大系统优化问题,电网建设方案应满足经济性、可靠性、适应性等诸多方面的要求。电网建设投资巨大,合理可行的优化方案可以取得巨大的经济和社会效益,但由于电网规划的复杂性和庞大工作量,传统方法一般仅对少量方案分析比选。用优化方法取代传统规划方法需要建立更实用有效的规划模型和优化方法。为此,本文提出基于系统可靠性的多阶段电网规划模型及其混合优化方法。
1 系统可靠性约束
系统可靠性计算通常建立在对研究系统进行故障后果分析的基础上,通过分析故障事件对系统所造成的影响,达到计算可靠性指标的目的。为确定故障事件对系统所造成的影响,需要通过潮流和稳定分析,研究系统在不同故障事件下的负荷供应能力(LSC)。LSC模型可表述为在满足系统节点功率平衡约束、发电设备和输电线路都不超过额定容量、节点负荷不超过最大需求等约束条件下,求系统最大供电能力。严格来说,此模型为一非线性规划模型。由于解决系统电压问题和稳定问题时,一般通过无功补偿设备配置和安全稳定装置更经济合理,系统可靠性计算的复杂性也要求简化计算,因此,在系统可靠性计算中通常对模型作合理简化,即不考虑系统电压问题和稳定问题导致的负荷供应不足或中断,仅考虑系统节点的有功功率平衡和发电设备、负荷、输电线路的有功功率约束,在此条件下,LSC模型可表示为:
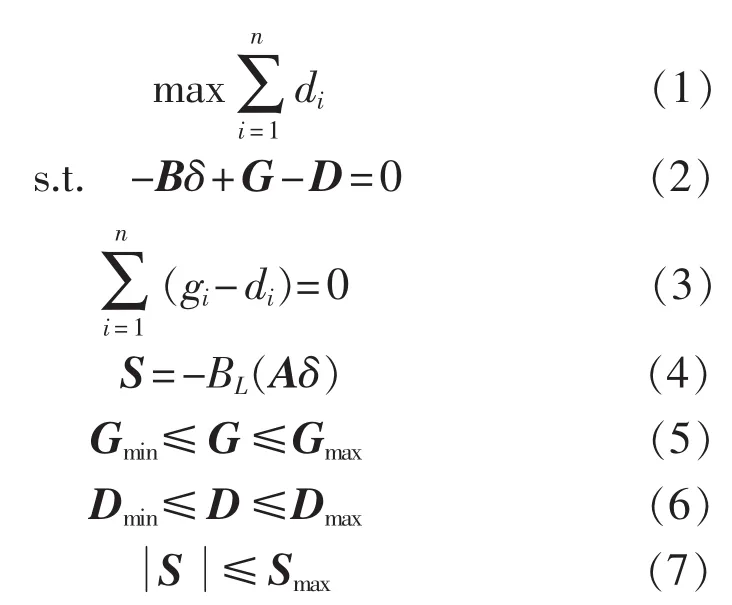
式中:D=(d1,…,dn),为节点负荷;di为节点 i上的负荷;n为网络节点数;Dmin、Dmax分别为最低负荷和最高负荷;G=(g1,…,gn),为电源出力;gi为节点i上的电源出力;Gmin、Gmax分别为电源最低出力和最高出力;S为支路传输功率,S=(s1,…,sl),sj为支路j的传输功率,l为网络支路数;Smax为支路最大传输容量;δ为节点电压相角;B为节点导纳矩阵;A为节点支路关联矩阵;BL为支路导纳对角矩阵。
在上述线性规划模型中,式(2)为直流潮流方程,由于平衡节点b的电压相角δb=0,为已知量,且平衡节点b的发电出力不受约束,自动平衡,因而需去掉平衡节点对应方程中的相关项,即删除导纳矩阵B及向量G、D、δ对应平衡节点b的行和列,导纳矩阵 B为(n-1)×(n-1)阶矩阵。但如果平衡节点的发电出力也受约束,则应增加全系统功率平衡方程式(3)。
由式(2)、(4)消去δ,可以得到LSC模型的更简洁形式:
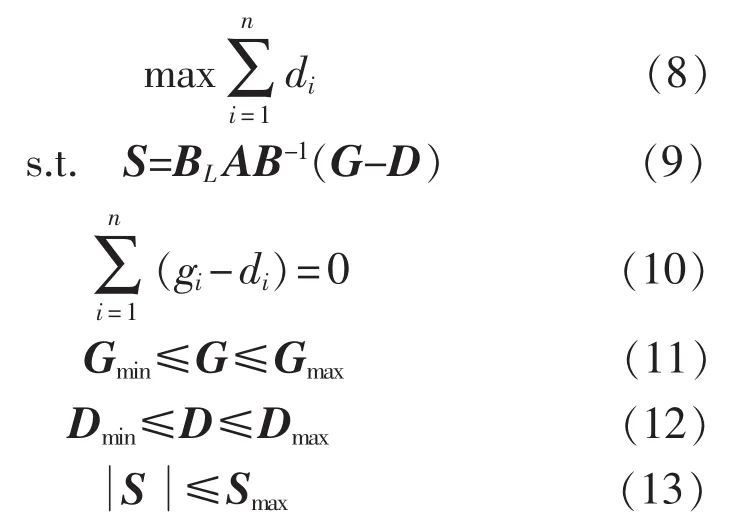
在LSC模型中,节点负荷削减方式不同,得到的模型也不同。上述模型采用的是保证系统最大供给的负荷削减方式,其它常用模型还有就近负荷削减方式、基于潮流跟踪的削减方式等[1-4],可根据电网情况选择。
系统可靠性指标可采用解析法或模拟法计算,前者通过确定性方法列举故障事件,后者运用概率方法列举,无论哪种方法都可以运用LSC模型对列举的故障事件进行后果分析,汇总后得到系统可靠性指标,如电力不足概率LOLP、电量不足期望值EENS等。若以f(x)表示系统可靠性指标,系统可靠性约束可表示为∶

式中:β为须满足的指标值。
2 基于系统可靠性的电网规划模型
基于系统可靠性准则的电网规划优化模型是在满足系统可靠性标准或准则的条件下,使方案在技术经济上达到最优,如造价、能耗等指标最低,可表示为:

式中:x=(x1,…,xm),为电网规划方案,表示系统可新增的发、输变电设备(发电机、线路、变压器等)入选状态的向量,m为系统可新增的发、输变电设备数量;h(x)为对应规划方案x的扩建费用。电网规划需要考虑系统可靠性要求与建设投资的平衡,通常仅要求满足某些特定故障下的系统可靠性,如部分系统元件单一故障下保证供电,即电网规划中的n-1规则。系统可靠性约束可简化为等式约束:

要严格求解上述整数规划问题,可采用隐含枚举法、分支定界法、割平面法等传统优化方法[5],但对于大规模电网规划问题,方案的组合数将随着待选线路的增加以指数规律递增,传统优化方法难以解决工程实际问题。因此,现代优化方法[6]成为求解此类问题的主要方法,如遗传算法、微粒子算法等。运用遗传算法求解上述模型,可按式(17)筛选符合条件的x,然后运用遗传算法等进行优化。但按式(17)筛选x,计算量大,不利于计算简化;加之新增设备较多的方案更容易满足可靠性约束而易于被选择为遗传初始种群,而新增设备较少的优化方案则不容易被选出;当给定系统满足可靠性约束的方案较少时,计算很难正常完成。
改进的模型可表示为多目标规划模型:
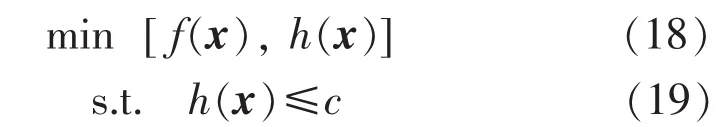
式中:c为系统扩建费用上限值,计算时满足系统扩建费用约束的方案才进行可靠性指标计算,对求解空间进行限制。按式(19)筛选的计算量极小,有利于减少计算量。若运用加权因子法求解,式(18)可表示为:
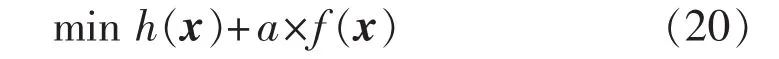
即以建设费用和系统可靠性指标综合最优为优化目标,通过权重乘子a协调目标函数与约束条件。在此模型中,系统可靠性约束条件(17)变为软约束,增大a值可使优化方案的可靠性指标减小,减小a值则可使优化方案的可靠性指标增大,且即使满足式(17)的解不存在,也能求得系统可靠性指标较小和建设费用较低的规划方案。
对于多阶段电网规划问题,可扩展为以下的多目标规划模型:
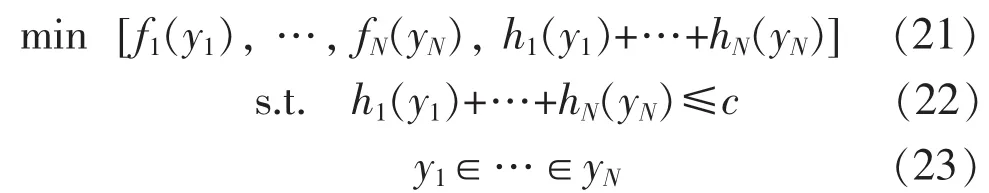
式中:yi表示电网规划第i阶段可新增的发、输变电设备入选状态的向量;fi(yi)为第i阶段对应规划方案yi的系统可靠性指标;N为规划阶段数;式(23)表示各阶段规划方案之间的关联关系,即在某阶段增加的发、输变电设备将在后续阶段一直存在。
3 遗传算法的应用
3.1 染色体编码
本文电网规划模型中各变量均为离散变量。如在单阶段电网规划问题中,可新增输变电设备状态变量xk={0,1}表示第k个可新增设备状态,0表示该设备不入选,1表示入选;在N阶段电网规划问题中,可新增发、输变电设备状态变量yk={ii=0,1,…,N}表示第k个可新增设备状态,i等于0表示该设备不入选,i为正整数时表示其在第i阶段入选。
由于仅利用遗传算法处理离散变量,采用整数编码非常合适和方便。这种编码方案与实际问题描述相符,整个染色体编码字串长度短,遗传操作也非常方便。
3.2 遗传操作
遗传算法的操作包括产生初始种群、选择、交叉和变异等操作。遗传算法的主要控制参数有种群规模mp、算法执行的最大代数mg、交叉率Pc、变异率Pm等,参数的选择对优化的进程和最终结果有影响,不同算法和染色体编码方案也会影响参数的取值。
在遗传算法中,选择提供了遗传算法的驱动力。如果驱动力太大,遗传搜索将过早终止;如果驱动力太小,进化过程将慢得难以接受。遗传选择操作有比例法、期望值法、排位次法和最优保存法等[7]。对于以系统缺电量期望值和建设费用最小为优化目标的电网规划问题,各方案的目标函数值不会有显著差距,比例法不能提供适当的选择压力,排位次法更易于调节合适的选择压力,可以直接根据个体目标函数值按从大到小顺序排列,利用预先确定的概率进行选择操作。
3.3 收敛判据
可作为收敛判据的有:目标函数在若干遗传代内不再发生变化;遗传进化代数超过规定的代数;优化目标值达到规定要求。
3.4 禁忌技术应用
为避免重复已做过的工作,采用了禁忌技术,即在优化过程中用禁忌表记录已经处理的过程和点的信息,利用该信息可以避免重复搜索过程。
4 混合优化方法
大规模电网规划方案的组合数将随着可新增发、输变电设备数的增加以指数规律递增,一个有m个可新增发、输变电设备的系统,对于N阶段电网规划问题其方案组合数为(N+1)m。使用遗传算法,虽然理论上可以大概率收敛于最优解,但收敛速度可能非常缓慢。为提高收敛速度和稳定性,可采用混合优化方法,即在规范的遗传算法中将局部优化作为辅助,由遗传算法进行种群中的全局广度搜索,局部优化则通过染色体中的局部深度搜索,使每一个新产生的后代在进入种群之前移动到局部最优点上。由于遗传算法和局部深度搜索的互补特性,混合优化方法能有效提高收敛性能和稳定性,通常比使用单一方法具有更好的效果[8-9]。
本文采用 “递延枚举优化”进行局部深度搜索,即通过推迟方案中新增发、输变电设备的投入阶段进行枚举比选,逐阶段对新增发、输变电设备逐个断开检查是否满足可靠性约束,如不满足则保留,满足则将此设备推迟到下一阶段投入,直至从规划方案中移除,考虑各种递延组合即可得到方案的局部最优解。
由于需对遗传算法得到的每一个方案进行递延枚举,计算量较大。为加快递延枚举比选过程,采用了分解递延枚举技术,每次仅考虑最多 r(r≤m)个新增设备被同时递延的情况,r可取1~ 3,重复此过程直至得到方案的局部最优解。此方法非常有效,因为随着优化过程的进展,由遗传操作得到的“初步解”中冗余设备已经不多,方案中多个新增设备同时被递延机会很小,因此可以不丢失最优方案并大大加快递延枚举比选过程。此外,还可采取隐含递延枚举技术:
(1)从开始阶段向后递延枚举,排除上一阶段不满足可靠性约束的方案。
(2)动态保存枚举过程得到的最优解,可排除建设费用高于最优解的方案。
5 算例
GARVER-6节点电网规划问题[10]的规划数据见表1和2。将电源出力和负荷水平划分为5个阶段,构成多阶段规划问题,如表3和4所示。以建设费用(假定与线路长度成正比)最小和满足n-1可靠性准则为目标和约束条件;LSC模型中考虑了对平衡节点发电出力的约束条件;遗传操作策略采用排位次法选择、一点交叉和均匀变异,交叉率Pc取0.9、变异率Pm取0.3、种群规模N取50。对于单阶段规划问题,电源出力和负荷水平取阶段5的数值,使用规范的遗传算法和混合优化方法求解,分别经过27代和15代求得最优结果,两种方法对此单阶段规划问题都有效,但混合优化方法收敛性能和稳定性更好。对于多阶段规划问题,优化结果及算法比较如表5和6所示,表中建设费用优化结果是以线路单位公里造价为基准值的标幺值(p.u.),使用规范的遗传算法的优化过程随遗传操作代数的增加趋于停滞,使用混合优化方法遗传操作仅13代就得到最优解,在收敛性能和稳定性方面具有明显优势,改变本算例参数或对其它算例计算也能得到类似结论。作为简化方法,仅对规范的遗传算法得到的最优结果(本例保留前10个方案)进行递延枚举优化,虽然能提高改进优化效果且耗时很少,但改进效果具有不确定性。

表1 电网已建线路特性
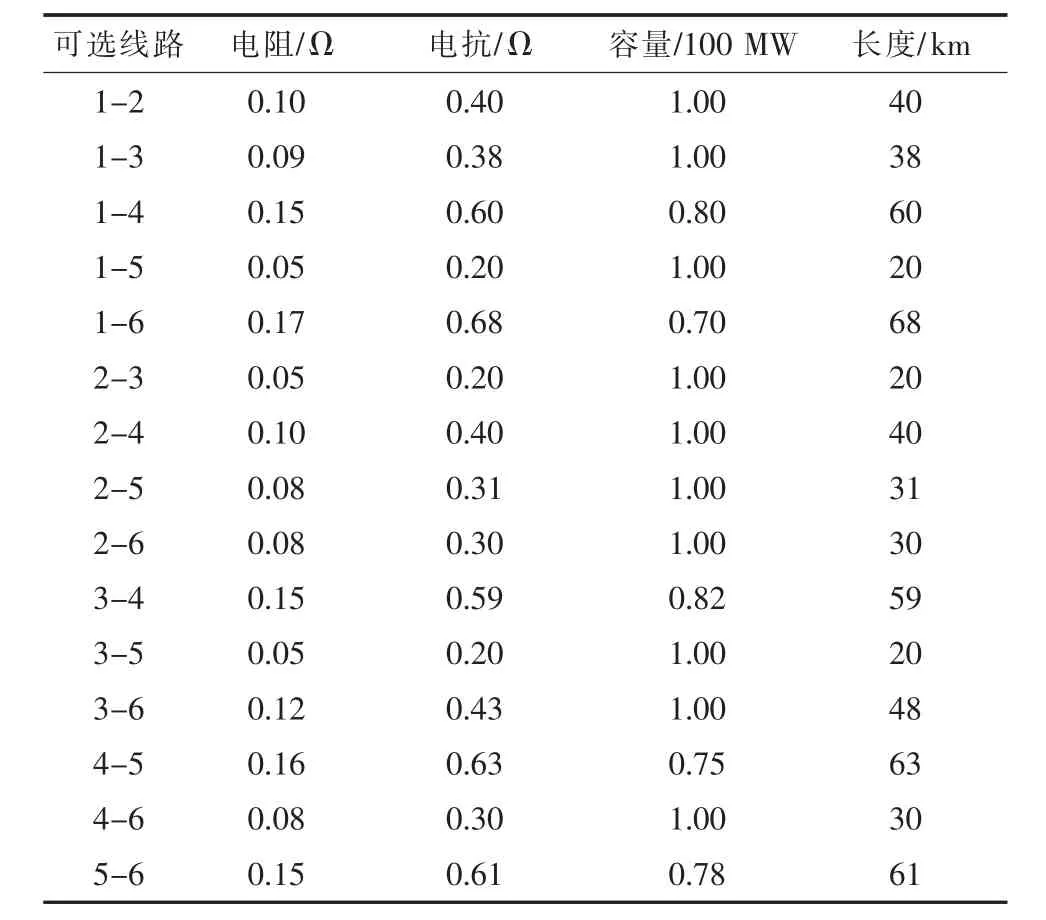
表2 规划可选线路特性
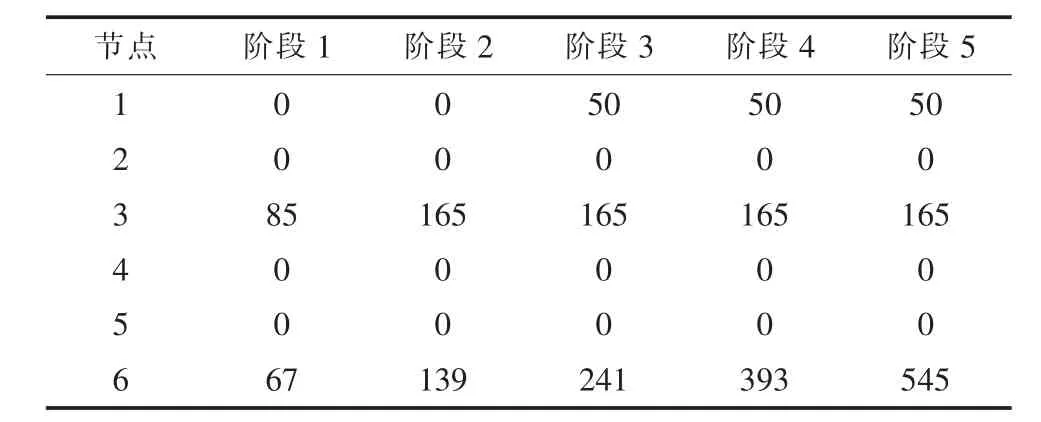
表3 多阶段规划的电源出力MW
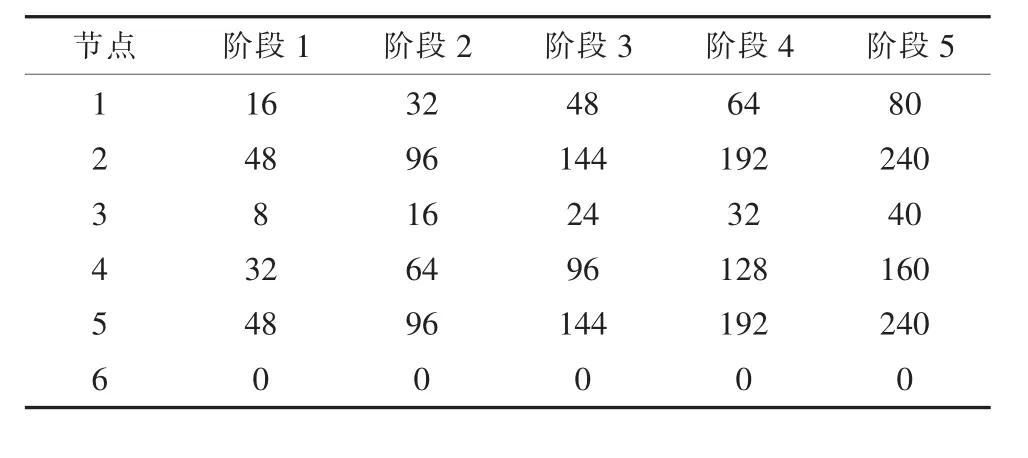
表4 多阶段规划的节点负荷MW
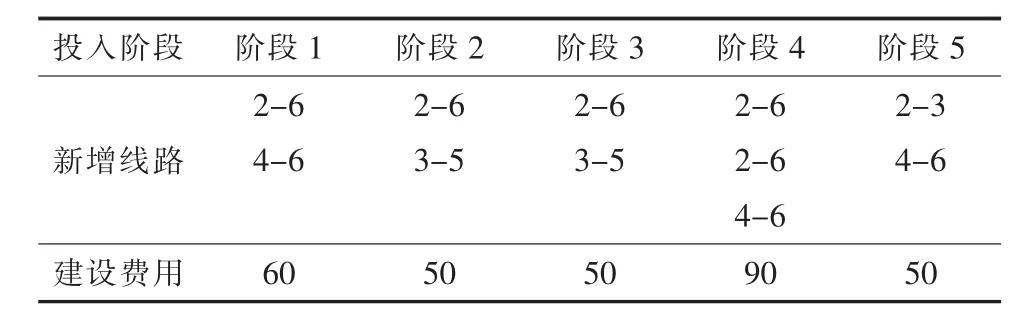
表5 多阶段规划优化结果
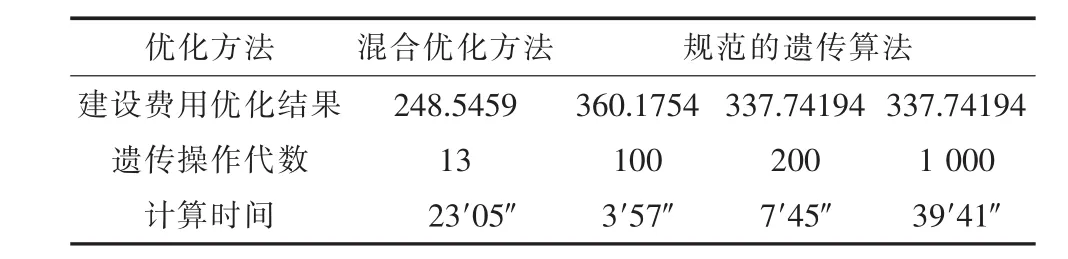
表6 多阶段规划优化方法比较
6 结论
电网建设投资巨大,合理可行的优化方案能取得巨大的经济和社会效益,但由于电网规划的复杂性和庞大工作量,传统规划方法一般仅分析比选少量方案。用优化规划方法取代传统方法需要建立更实用有效的规划模型和优化方法。
基于系统可靠性的多阶段电网规划模型,在满足系统可靠性准则的前提下优化系统发展过程中各阶段建设费用,可满足电网规划的基本要求。运用混合优化方法求解此优化规划模型,由于遗传算法和局部深度搜索的互补特性,能有效提高收敛性能和稳定性,比使用单一方法具有更好的效果。运用递延枚举优化进行局部深度搜索,即通过推迟方案中新增发、输变电设备的投入阶段进行枚举比选,考虑各种递延组合即可得到方案的局部最优解。运用分解递延枚举和隐含递延枚举技术可加快递延枚举过程。算例验证了规划模型及其优化方法的实用性和有效性。
[1]吴开贵,吴中福.大电网可靠性计算中的负荷削减策略[J].重庆大学学报,2003,26(7)∶28-31.
[2]刘洋,周家启.大电网可靠性评估最优负荷削减模型[J].重庆大学学报,2003,26(10)∶52-55.
[3]幸荣霞,姚爱明,谢开贵,等.大电网可靠性影响分析的潮流跟踪方法[J].电网技术,2006,30(10)∶54-58.
[4]赵渊,周家启,刘洋.发输电组合系统可靠性评估中的最优负荷削减模型分析[J].电网技术,2004,28(10)∶54-58.
[5]陈宝林.最优化理论与算法(第2版)[M].北京:清华大学出版社,2005.
[6]邢文训,谢金星.现代优化计算方法(第2版)[M].第2版.北京:清华大学出版社,2005.
[7]熊信银,吴耀武.遗传算法及其在电力系统中的应用[M].武汉:华中科技大学出版社,2002.
[8]玄光男,程润伟.遗传算法与工程优化[M].于歆杰,周根贵,译.北京:清华大学出版社,2004.
[9]丘文千.混合优化方法及其在电力系统无功优化中的应用[J].中国电力,2009,42(4)∶45-48.
[10]孙洪波.电力网络规划[M].重庆:重庆大学出版社,1996.
(本文编辑:徐 晗)
Multistage Grid Planning Models and Hybrid Optimization Algorithms
QIU Wen-qian1,QIU Yang2
(1.Zhejiang Electric Power Design Institute,Hangzhou 310012,China;2.Hangzhou Electric Power Bureau,Hangzhou 310009,China)
The grid planning models are presented to meet power system reliability criteria as constraints and to reduce the stages construction costs as optimization goal.To solve the models,hybrid optimization methods are developed so that the convergence and stability of the algorithms are improved effectively.Deferred enumeration optimization is used for local depth searches,and then local optimal solutions are obtained.Decomposition and implicit deferred enumeration technology is used to accelerate the enumerating process.The practicability and effectiveness ofthe planning models and relevantoptimization methods are verified with calculation cases.
power system reliability;stochastic planning;uncertain planning;multistage planning;genetic algorithm
TM715
:A
:1007-1881(2010)10-0001-05
2010-06-29
丘文千(1952-),男,上海人,教授级高级工程师,长期从事电力系统规划、工程设计与技术管理工作。

