遥感图像去雾算法研究
石文轩 李 婕
(武汉大学 电子信息学院,武汉 430079)
1 引言
图像去雾是一个非常具有挑战性的研究课题,因为在缺少深度信息的情况下,对单张含雾图像进行恢复是一个约束不足的恢复问题。大多去雾方法采用对图像附加限制,增加辅助数据或使用多幅图的方式对图像进行去雾。在有雾的遥感图像中景物细节信息依稀可见,图像去雾的目的便是消除图像中的雾对景物的影响,还原景物的本来面目。
对比度增强法是通常使用的去雾操作方法之一,该方法可以通过灰度调整技术实现,但是这种方法仅取决于像素的灰度值,而忽视了图像中各物体之间的空间关系。对比度增强法包括线性匹配、直方图拉伸、直方图均衡以及伽马校正等,这些方法在一般的图像处理软件中都可以实现。Larson[1]提出了一种更为成熟的色调重建方法,该方法可以用来渲染具有高动态范围的图像。在通常的场景中,雾的厚度在图像的不同位置是有区别的,因此,雾对每个像素的影响也不尽相同。由于以上方法对整幅图像不同位置的处理方式是一样的,并没有考虑图像中局部雾的厚度不一的情况,因此,上述方法具有一定的局限性。
图像中的雾会造成的影响既包括加性影响也包括乘性影响,加性噪声为光学系统的背景噪声,而乘性噪声是由于系统的信道不理想造成的。如果不能处理好加性噪声影响,噪声就会在信道中产生正反馈放大,从而增大图像中乘性噪声影响的程度。
仅使用Retinex算法就可以有效地去除图像中的雾,使雾中的景物清晰展现,但去雾后的图像色彩偏灰,使原图中的彩色信息大量损失。本课题提出了一种基于Retinex算法和色度比的去雾算法,引入了原图中的色彩信息,能在去雾的同时,保留图像的色彩。
2 Retinex算法
由Land提出的Retinex思想[2-4]认为颜色的恒常性不会受到周围照明环境的影响,仅与人眼的视觉系统和目标物体表面的反射性质有关。Retinex模型主要是将理想图像分解为入射光和物体的反射系数2部分,可由式(1)表示。

式中 L是捕获的图像;I是入射光分量,直接决定了一幅图像能达到的动态范围;R反映了物体表面的材质对光的反射性质。采用Retinex理论的目的就是从捕获的图像L中恢复出R,也就是要从图像中滤除入射光部分得到物体本身的面貌。
基于中心/包围的Retinex算法是近年来的研究热点,主要包括单尺度Retinex算法和多尺度Retinex算法。
2.1 单尺度Retinex算法
单尺度Retinex算法(Single Scale Retinex,SSR)是建立在光照-反射模型的基础上的。人眼对物体的亮度感觉取决于环境光的照明和物体表面材质对照明光的反射2部分,可表示为

式中 L(x,y)表示图像中坐标位置为(x,y)的像素的亮度值;I(x,y)为该点的照明强度函数;R(x,y)为反射函数。
第l(l=1,2,3)个颜色通道的光强值Ll是照明强度Il与反射强度Rl的乘积,对于图像中第x行第y列的像素,其l通道的亮度值可表示为:

由于亮度的对数形式更接近人眼的感知能力,并且采用对数形式可以将复杂的乘法运算变成简单的加法运算,因此,可以将上式等号两边取自然对数,表示为:

如果 rl(x,y)=1nRl(x,y),则:

由于Il(x,y)变化平缓,能量集中在低频部分。将Il(x,y)写成包围函数与所在通道的亮度值的卷积形式,相当于对原图像进行低通滤波,就可以得到Retinex算法的基本表达形式:

式中 Ll(x,y)是所输入图像的l通道在坐标(x,y)的亮度值,亮度值的取值范围是[0,255],取值越小代表该像素越暗,越大代表该像素越亮,数值为0时表示黑,数值为255时表示白;F(x,y)是中心/包围函数,也称为权重函数;rl(x,y)是反射系数。
Zia-ur Rahman等人[5]将数字图像的中心/包围函数定义为:

其中 A是归一化常数;σ是高斯包围函数的标准差。
对于σ较小的中心/包围函数经过单尺度Retinex算法增强后突出了图像的细节信息,而对于σ较大的中心/包围函数经过单尺度Retinex算法增强后呈现出原图像的色调[6]。但是基于单尺度Retinex算法直接用于去除雾的效果并不明显,所以需要对单尺度Retinex算法进行改进,找到更为理想的方法去除图像中的雾。
2.2 多尺度Retinex算法
由于单尺度中心/包围函数中标准差 σ选取的不同会直接影响到被处理图像的彩色呈现,为了使彩色图像呈现与视觉可接受的动态压缩范围之间得到平衡,由Daniel J.Jobson等提出了多尺度Retinex算法(Multiple Scale Retinex,MSR)[7],在多尺度Retinex算法中,选取不同的标准差σ分别计算,并且给计算结果赋予一定的权重值。该算法可表示为

其中 l表示通道号,l=1代表红色通道,l=2代表绿色通道,l=3代表蓝色通道;Wk是对应的Fk计算结果的权重值;k是中心/包围函数或尺度的数量。
Fk可由式(3)求得:

其中 A是归一化常数;σk是尺度为k的高斯包围函数的标准差,σk的大小控制了包围的范围。当N=1时,多尺度Retinex算法退化为单尺度Retinex算法。
通常情况下,k=3,且 W1=W2=W3=1/3,如果将 σk的大小设定为大、中、小3个值,则多尺度 Retinex算法同时包含了多个尺度的特征。该算法既能在一定程度上突出图像的细节信息,又能在一定程度上使图像呈现出原图像的色调,这样就提供了完整的颜色恒常性和动态范围压缩,使彩色图像再现[6]。试验证明多尺度Retinex算法比单尺度Retinex算法的图像增强效果更为理想。
3 基于Retinex算法和色度比的图像增强算法
多尺度Retinex算法在增强彩色图像时,有些通道的像素亮度很容易达到饱和失真,从而改变图像中物体本身的颜色。因此,为了保持颜色的恒常性需要考虑缓和颜色的饱和度,弥补多尺度Retinex算法的缺陷。
Retinex算法不仅可以增强灰度图像,同时也能增强彩色图像。但是对于拍摄到的雾天图像,仅仅用Retinex算法进行图像增强无法提高图像的对比度,因此,需要对经过Retinex算法处理的图像的直方图进行校正。如果,处理后的图像没有充分利用显示设备所允许的显示灰度范围,就会导致显示出的图像对比度较低,图像中的一些细节信息很难被察觉。因此,可以对这样的图像进行对比度的线性拉伸。对于分辨率为M×N的8位量化图像,线性拉伸就是将图像的灰度范围由其原本的灰度范围[min,max]拉伸到[0,255],并可以用式(4)表示:

假设图1(a)为一幅原始图像的直方图,其中min为图像中所有像素的最小灰度值,max为图像中所有像素的最大灰度值。线性拉伸就是将灰度级由原来的[min,max]拉伸到[0,255],如图1(b)所示。

图1 直方图线性拉伸
从图1(a)中可以看出,图像大部分像素点都集中在[Plow,Phigh],而超出这个范围的像素点,也就是灰度范围分布在[min,Plow]和[Phigh,max]的像素点数量很少,这些灰度的像素点基本不对整幅图像构成影响,因此,在线性拉伸时对这部分像素点可以忽略不计。这时,线性拉伸公式可以由式(4)改写为式(5):
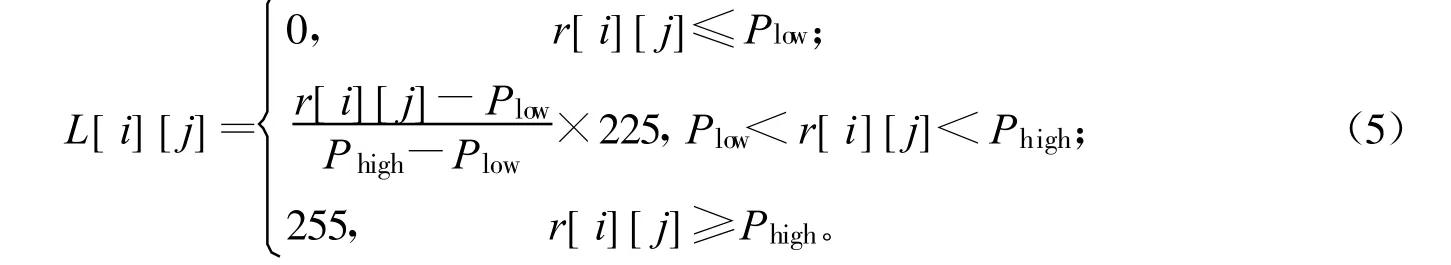
式中 Plow称为下饱和点;Phigh称为上饱和点。由式(5)可知上饱和点和下饱和点的选取对线性拉伸起关键的作用。
芮义斌等[8]提出了一种自适应的线性拉伸方法。在正态分布中,假设图像的灰度均值为 μ,标准差为σ,那么图像中的绝大部分像素都会落到区间[μ-3σ,μ+3σ]内,与图像的灰度均值 μ相差超过3σ的像素点可以忽略不计。因此,自适应的线性拉伸方法的下饱和点取Plow=μ-3σ,上饱和点取Phigh=μ+3σ,然后根据式(5)对Retinex算法处理后的图像进行直方图线性拉伸。这里采用多尺度Retinex算法,并且中心/包围函数中的尺度常数分别取为15,80,250,对含雾彩色图像的处理结果如图2所示。

图2 多尺度Retinex算法对含雾彩色图像的处理
从图2中可以看到,由于多尺度Retinex算法可以分别对R、G、B三个谱段的图像进行去雾,因此,在图像中的平坦区域,对这3个谱段进行去雾处理后,3个谱段的灰度值计算结果近似相等,将3个谱段的处理结果合成为彩色时就会呈现偏灰的色彩,从而失去了图像本身各个谱段的颜色比例关系。
由于单独使用多尺度Retinex算法对含雾的彩色图像处理会导致图像色彩偏灰。本课题对基于多尺度Retinex算法的去雾算法进行了相应的改进,并加入了每个像素的色度比信息。假设采用的中心/包围函数中的尺度常数分别为15,80,250,则用多尺度Retinex算法处理得到的3个谱段的计算结果为:

其中 Wk是每种尺度计算结果所占的权重,一般情况下取W1=W2=W3=1/3。
如果原图的3个谱段用R-original,G-original,B-original表示,那么本文引入的3个谱段的色度比可表示为:
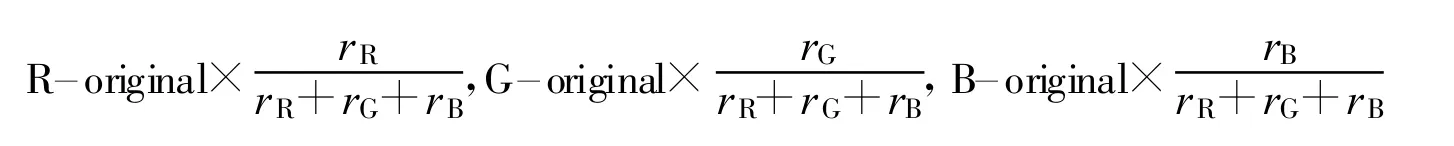
那么,最终的恢复图像的对数形式可以表示为:

其中 l=R,G,B,W1=W2=W3=W4=1/4。对式(6)进行指数运算,那么增强后的图像可表示为:

由式(7)计算出的图像能克服雾引起的图像对比度不高的问题,但是处理结果的动态范围较小。因此,可用直方图线性拉伸的方法(式(5))对式(7)的计算结果的每个谱段进行线性拉伸,最后将3个谱段的拉伸结果合成为最终的彩色图像。处理后的图像增大了图像的对比度,能满足人眼的视觉要求。
由式(6)可知,本文提出的算法耦合了每个像素的色度比信息,使增强的图像还原了原有的色彩,克服了多尺度Retinex算法处理彩色含雾图像时产生的图像偏灰的问题。用该算法处理得到的图像如图3所示。

图3 基于Retinex算法和色度比的图像增强算法
表1列出了原始含雾图、多尺度Retinex算法处理结果和本文提出方法的标准差比较。标准差大,则说明图像的对比度高。从表中可以看出,多尺度Retinex和本文方法处理后,图像的标准差都有明显的提高。使用本文方法处理后的图像色彩更为逼真。

表1 图像灰度标准差比较
4 结束语
本文针对含雾的遥感图像复原,提出了一种新的遥感图像去雾处理的方法——基于Retinex算法和色度比的图像增强算法。该算法克服了直方图均衡法容易引起图像色彩的畸变和基于Retinex算法的自适应线性拉伸方法处理后的图像偏灰等问题。该算法在用Retinex算法进行图像恢复的过程中引入了原图像的色彩信息,改善了处理后的图像的色彩。试验表明,该算法能有效地去除遥感图像中雾的成分。
[1]Larson G W,Rushmeier H,Piatko C.A Visibility Matching Tone Reproduction Operator for High Dynamic Range Scenes[J].IEEE Transactions onVisualization and Computer Graphics,1997,3(4):291-306.
[2]FinlaysonG D,Hordley S D,Drew M S.Removing Shadows From Images using Retinex[C].Proceedings of IS&T/SID Tenth Color Imaging Coference,Scottsdale,AZ,United States,2002:73-79.
[3]Meylan L,Susstrunk S.Color Image Enhancement Using a Retinex-based Adaptive Filter[C].Proceedings of IS&T Second European Conference on Color in Graphics,Image,andVision(CGIV 2004),2004,2:359-363.
[4]Sun Bo,Chen Weifang,LiHongyu,et al.Modified Luminace BasedAdaptive MSR[C].Proceedings of the Fourth International Conference on Image and Graphics,2007:116-120.
[5]Jobson D J,Rahman Z,Woodell G A.Feature Visibility Limits in the Non-linear Enhancement of Turbid Images[J].SPIE,2003,5108:24-30.
[6]江兴方.遥感图像去云方法的研究及其应用[D].南京理工大学博士学位论文,2007.
[7]Rahman Z,Jobson D,Woodell G.Multiscale Retinex for Color Image Enhancement[M],1996.
[8]芮义斌,李鹏,孙锦涛.一种图像去薄雾方法[J].计算机应用,2006,26(l):154-156.

