小直径单立柱上的波浪荷载研究

韩非非，张 玮，陈 恺

（河海大学港口海岸与近海工程学院，南京210098）

由于海洋环境的特殊性，海洋建筑物会受到波浪、海流、海冰等动力作用，承受着与陆地环境不同的外部荷载。波浪荷载计算是海洋建筑物设计中不可或缺的一个环节，已发展成为多种计算理论［1］。目前，研究海洋建筑物上的波浪荷载时，通常采用2种方法［2］：一种是“设计波”法，用一个给定波浪周期和波高的波浪，代表一定环境下的最大波，此法只能研究规则波；另一种是“设计谱”法，研究不规则波浪的长期作用规律，其中波谱是给定波高和周期相应的波谱。

无论采用“设计波”法还是“设计谱”法，数值模拟已成为一种趋势，在波浪荷载研究中被广泛应用。然而在数值模拟的基础上，最好能有一定的实测数据或可作为验证资料的数据，以此来验证数值模拟的准确性，这是目前波浪荷载研究中的一个空缺。然而用实测数据和实验数据作为验证资料，需要投入大量的人力物力，且人为因素会造成许多误差，有很大的局限性。用理论计算值作为验证资料则方便、准确。

本文以微幅波波浪理论为例，采用“设计波”法计算小直径立柱上的波浪荷载，利用计算小直径立柱上波浪荷载的常用公式——Morison公式，得到波浪荷载的理论计算值［3］，以此作为验证资料，建立有限元模型，将模型计算值与理论计算值进行对比，进而研究计算参数计算时长（time）和时间步长（substeps）的最佳值。

1 单立柱上波浪荷载的理论计算方法

1.1 Morison方程

目前，计算作用于小尺度立柱上的波浪荷载时，最常用的公式是Morison方程［2］，虽然只是计算波浪荷载的半经验公式，但已在工程中得到广泛应用。

根据Morison方程，作用在圆柱上的作用力可以分为两部分：一部分为由于水质点运动而产生冲击桩的拖曳力，由流体质点水平速度引起；另一部分为波浪水质点运动引起的对桩柱的惯性力，由流体质点水平加速度项引起［3］。公式的物理意义在于将波浪作用于桩柱结构上的力分解为速度分力和惯性分力，再按力矢合成原理，将速度分力和惯性分力叠加，其合力是波浪对桩柱结构的作用力［4］。

小尺度构件垂直于其轴线方向单位长度上的波浪力F为

式中：FD为拖曳力；FI为惯性力。其分别可表示为

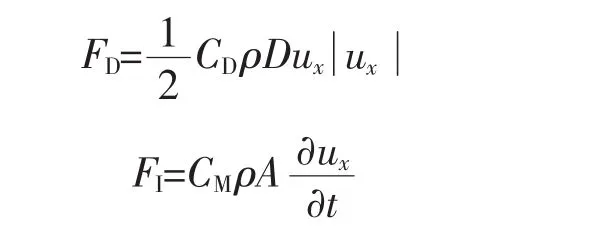
式中：D为结构物的特征尺度；A为结构物横截面面积；ρ为流体的密度；ux为垂直于构件轴线水质点速度分量。当海流与波浪联合作用时，为波浪水质点的速度矢量与海流速度矢量之和在垂直于构件方向上的分量；∂ux/∂t为垂直于构件轴线水质点加速度分量。当海流与波浪联合作用时，为波浪水质点的速度矢量与海流加速度矢量之和在垂直于构件方向上的分量；CD为阻力系数；CM为惯性系数（或质量系数）；对圆形构件，可取CD＝0.6～1.2，CM＝1.3～2.0。

任意相位时作用于整个圆柱体上的总水平波浪力为

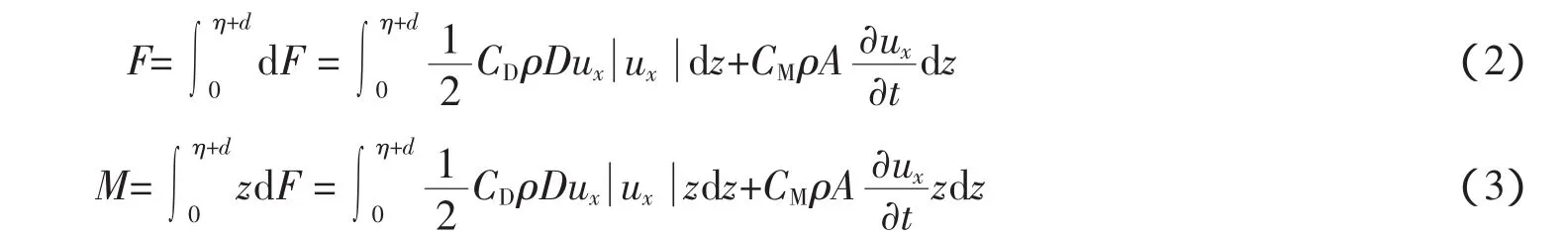
1.2 微幅波表示的波浪理论

式（2）和式（3）中的ux根据选取的波浪理论具有不同的表达形式，常用的波浪理论有线性波理论和非线性波浪理论。线性波理论主要是Airy波浪理论，非线性波理论主要包括Stocks波浪理论、椭圆余弦波理论和流函数理论［5］。

本文以微幅波理论为例，得到微幅波理论表示的单个直立柱体上的水平总波浪力和水平总波浪力力矩，如下式所示

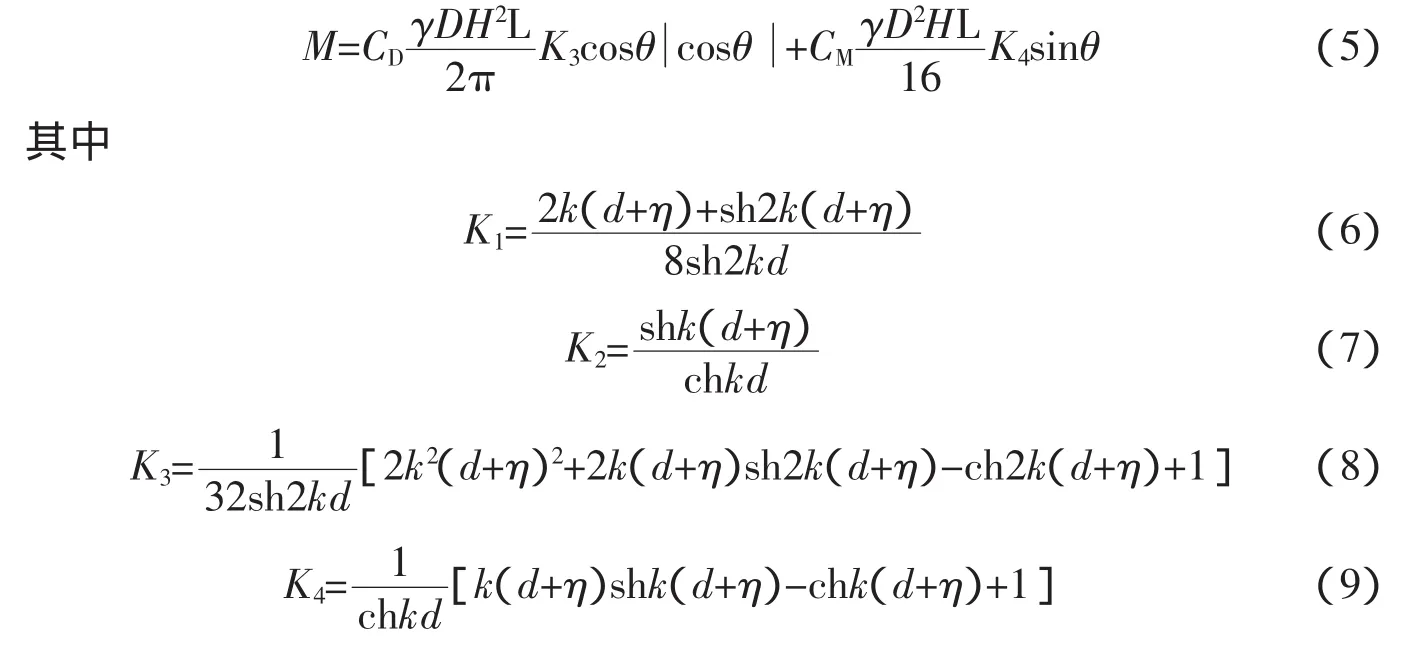
1.3 计算实例

采用微幅波波浪理论表示的Morison公式，计算一个直立桩柱上的波浪荷载，基本参数见表1。计算时代入不同相位角对应的K1、K2、K3和K4值，得到理论计算结果（表2）。

表1 计算基本数据Tab.1 Basic data for calculation

2 用ANSYS计算单立柱上的波浪荷载

2.1 单立柱上的总波浪力

本文按照上述参数建立有限元模型（图1）。采用微幅波波浪理论，入射角为0°，输入水流参数后，计算得到单立柱上的总波浪力与总波浪力力矩。

图1 有限元模型Fig.1 Finite element model

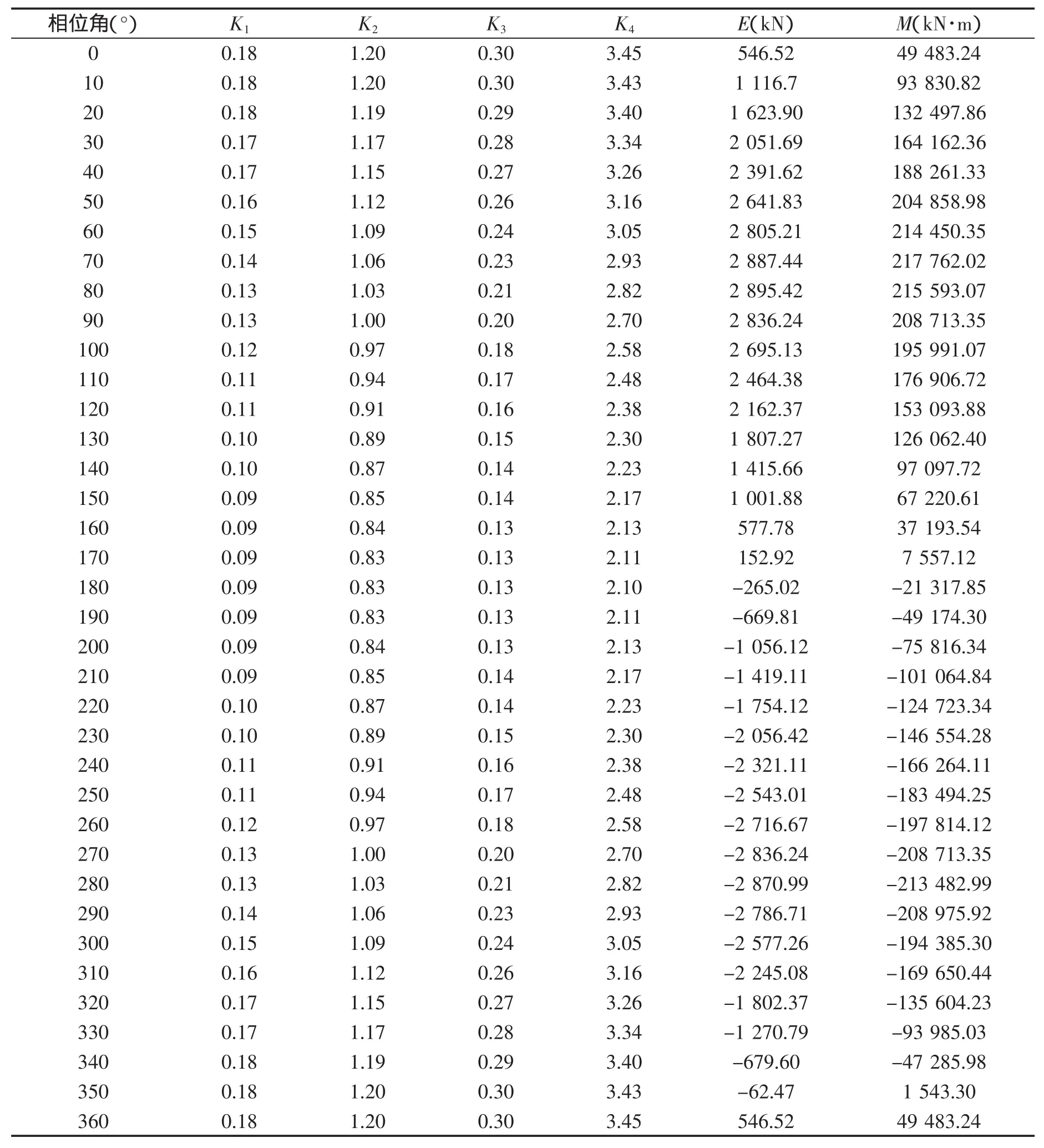
表2 单立柱上波浪荷载的理论计算结果Tab.2 Theoretical calculation results of wave load on single pile

一般数值模拟的误差来源于3个方面：模型误差、舍入误差和截断误差。

数值计算时通常会对实际问题进行简化。由简化后的数学模型与实际问题的差异产生的误差即为模型误差。计算时用精度有限的有理数代替精度无限的无理数而产生的误差即为舍入误差，此误差由计算精度引起。截断误差是由不含舍入误差的积分步长产生，减小积分步长可以减小截断误差，但是会增加计算时间，且高阶算法将会增加数值的不稳定性。因此在数值模拟时，在不计模型误差的基础上，时间步长的选取存在一个恰当值［6］。

表3 不同计算时长的相对误差范围Tab.3 Relative error range of different calculation times %

本文通过与理论计算值的比较，发现对小直径立柱的波浪作用进行数值模拟时，计算时长和计算步长对计算结果的影响较大，并存在一个可使计算结果趋于稳定的恰当值。计算结果与理论值的误差范围见表3和表4。从表3和表4中可以看出，当计算时长大于15倍波浪周期，时间步长约为波浪周期的1/20时，计算结果与理论值的相对误差较小。

由计算结果（表5）可以看出，用本文的计算模式计算单立柱上的波浪荷载时，其结果十分接近理论计算值，相对误差基本维持在3%以内。

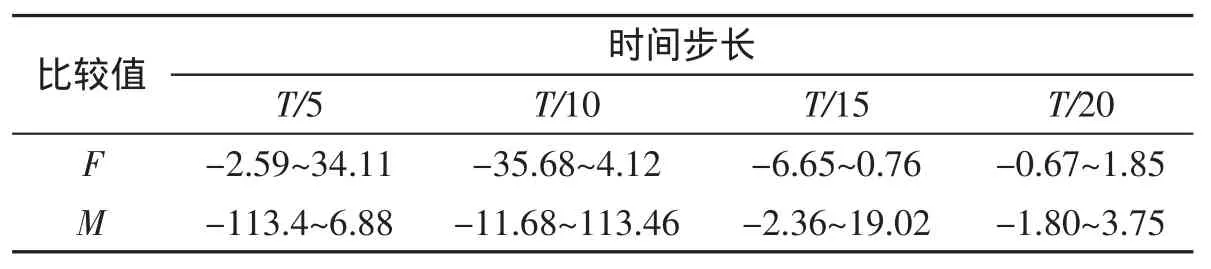
表4 不同时间步长的相对误差范围Tab.4 Relative error range of different calculation time steps %

2.2 不同水深时单立柱上的波浪荷载分布

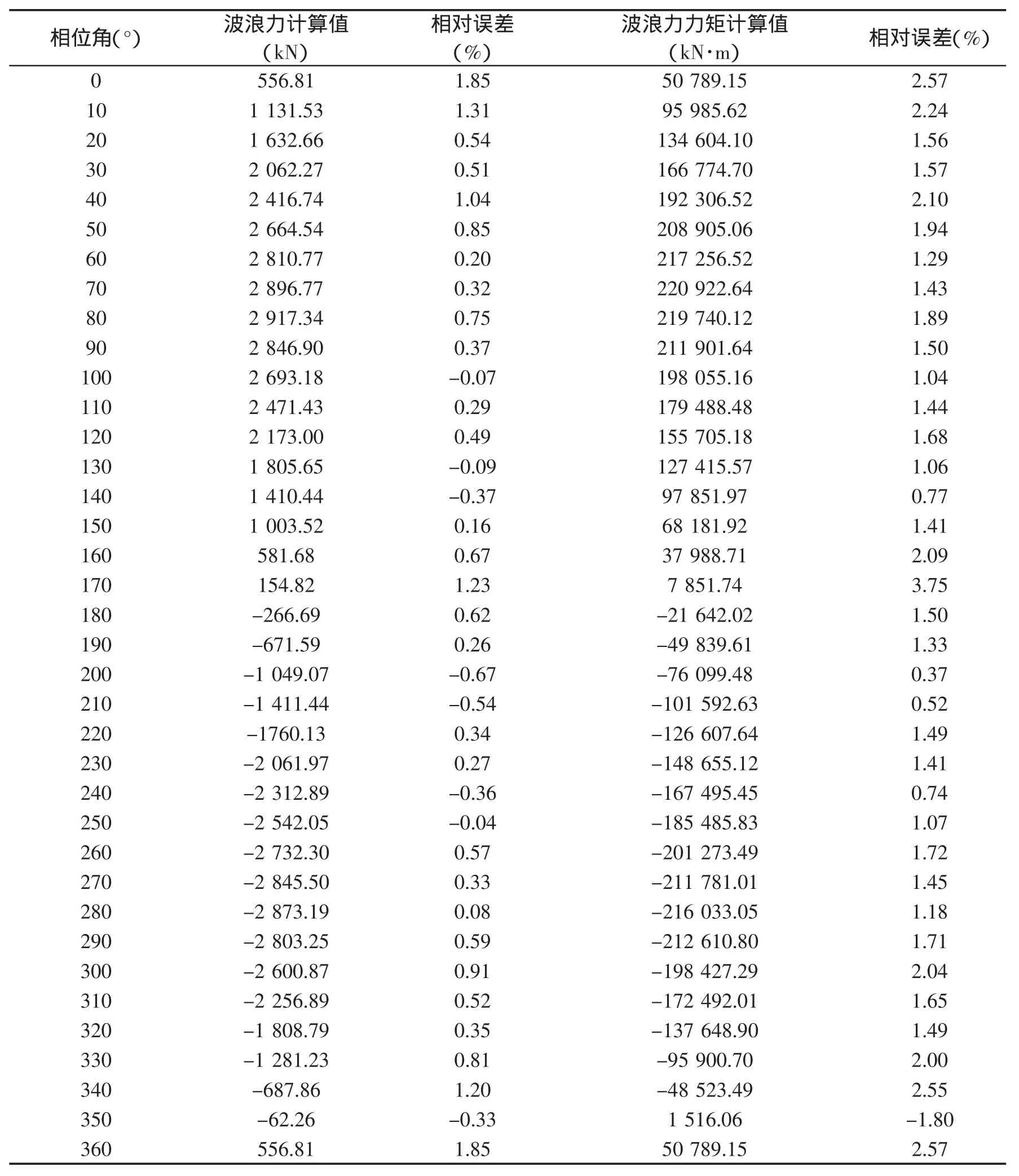
表5 模型计算值与理论计算值的比较Tab.5 Comparison of model calculation and theoretical calculation value

计算深水区单立柱上的波浪荷载时，发现立柱刚度较小时，计算结果会不稳定，严重偏离理论值（图2）。若增大立柱刚度，可使计算结果与理论值符合良好。

图3和图4分别给出100 m水深和40 m水深时对应的波浪力分布，观察总波浪力最大值对应的单立柱上波浪荷载的分布，可以看出立柱上波浪荷载随水深呈现递减的趋势，且集中在静水面附近。

不同的是，深水时波浪力沿水深急剧减小，减小到一定值后基本保持不变，并在水底附近达到最小值；浅水时波浪荷载沿水深逐渐减小，变化较为均匀，在水底处达到最小值，且此时底部管桩所受的波浪力远大于深水底部管桩所受的波浪力。由波浪理论可知，此变化规律符合质点水平速度随水深的分布规律［7-8］。

以上分析表明，在采用ANSYS模拟单立柱上的波浪作用时，其计算结果合理可信，可将此波浪力计算方法推广到工程应用中。

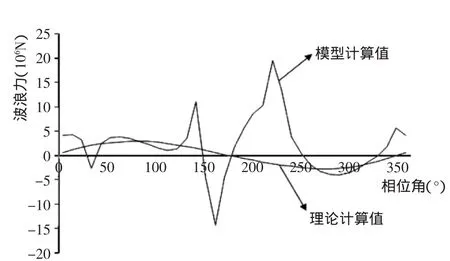
图2 小刚度立柱上的波浪荷载Fig.2 Wave load on small stiffness pile

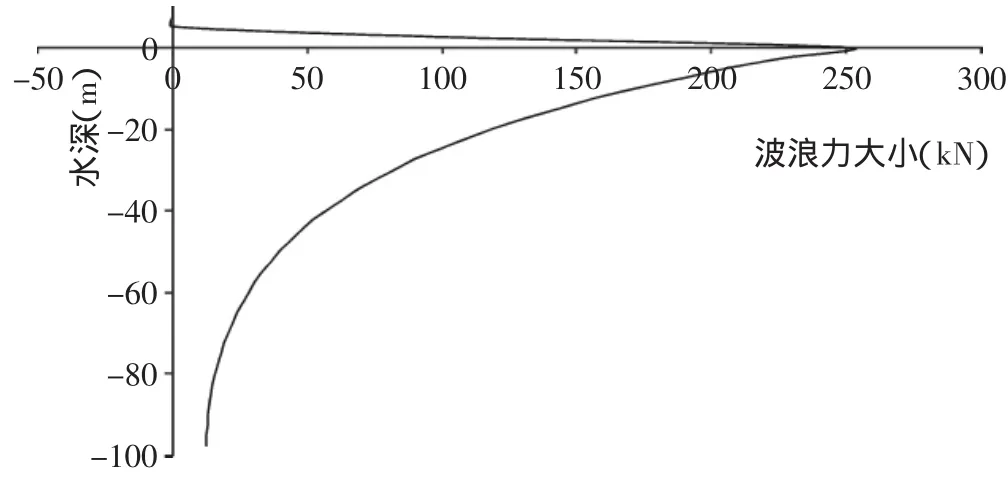
图3 100 m水深单立柱上波浪荷载沿水深的分布Fig.3 Distribution of wave load on single pile on 100 m depth

图4 40 m水深单立柱上波浪荷载沿水深的分布Fig.4 Distribution of wave load on single pile on 40 m depth

3 结论

（1）目前计算作用在小直径立柱上的波浪力时，常用Morison公式，本文用微幅波波浪理论表示的Morison公式计算得到随相位角变化的单立柱上的总波浪力。

（2）本文用ANSYS模拟小直径单立柱上的波浪作用，在不考虑模型误差的基础上，发现计算总时长和时间步长对计算结果影响较大，并存在一个可使计算结果趋于稳定的恰当值，即当计算时长大于15倍波浪周期，时间步长约为波浪周期的1/20时，计算结果较为准确。

（3）在计算深水区单立柱上的波浪荷载时，发现立柱刚度较小时，会使计算结果不稳定，严重偏离理论值。若增大立柱刚度进行计算，可使其与理论值符合良好。

（4）由本文推荐计算模式得到的计算结果与理论计算值十分接近，波浪力分布沿水深的分布符合波浪理论，可将此计算波浪力的方法推广到工程实践中。

本文计算的波浪条件比较理想，计算模型较为简单，而在工程实践中，计算模型的简化以及波浪理论的选取等都会对计算结果产生影响。因此对于较复杂的实际问题，还有待更深入的研究。

［1］赵丽娟.构筑物与波浪相互作用的研究［J］.水运工程，2003（12）：21-24.ZHAO L J.An Approach to the Interaction between Structures and Wave［J］.Port&Waterway Engineering，2003（12）：21-24.

［2］张玲.小直径桩柱波浪荷载的计算分析及程序实现［D］.青岛：中国海洋大学，2004.

［3］竺艳蓉.海洋工程波浪力学［M］.天津：天津大学出版社，1991.

［4］徐伟国.桩柱结构波浪力计算新探［R］.宁波：第三航务工程局第四工程处，1985.

［5］徐进，石兆东，张康.基于 Morison 方程的海底管道疲劳寿命分析［J］.承德石油高等专科学校学报，2009，11（4）：21-23.XU J，SHI Z D，ZHANG K.Morison Equation Based Fatigue Life Analysis of Submarine Pipeline［J］.Journal of Chengde Petroleum College，2009，11（4）：21-23.

［6］李庆扬，王能超，易大义.数值分析［M］.北京：清华大学出版社，2001.

［7］张宁川，俞聿修.小直径桩柱上波浪力峰值的短期分布［J］.海洋工程，1993，11（3）：20-27.ZHANG N C，YU Y X.The short-term distribution of the peak value of wave forces on a pile［J］.The Ocean Engineering，1993，11（3）：20-27.

［8］邱大洪.桩群上的最大总波浪力［J］.海洋学报，1981，3（1）：157-164.QIU D H.The Maximum Total Wave Forces on Pile Groups［J］.Acta Oceanologic Sinica，1981，3（1）：157-164.