空基平台无源定位精度分析
武宜川,潘冠华,罗双喜
(中国船舶重工集团公司江苏自动化研究所,江苏 连云港 222006)
在各种精确探测定位技术中,无源探测定位技术因其独特的技术优势和使用价值,越来越显示出其重要的作用和地位。无源定位技术具有作用距离远、隐蔽性能好的优点,对于提高系统在电子战环境下的生存能力和作战能力具有重要作用,在空载对地、对海攻击以及远程预警系统中已得到广泛的应用。无源定位系统的承载平台可以分为多种,如空基平台,星载平台,地面平台,海面平台等等。而空基平台由于其独特的优势,成为目前搭载无源定位设备的良好平台。介于普通航空飞机飞行空间和航天器轨道空间之间的中高空区域是目前现有大部分防空监视系统的盲区,且处于绝大多数防空导弹杀伤区之外。工作在这个区域的空基平台有飞艇、低轨卫星、无人飞行器等[1]。
空基平台的测量传感器主要采用红外传感器。由于红外传感器通过接收目标辐射的能量进行定位和跟踪,不向空中辐射任何能量,因而不易被侦察或定位,具有很强的抗干扰能力。该传感器通过测量三维空间内目标的方位角和俯仰角进行定位,算法简单,计算量小,运算速度比较快。
本文主要针对单空基平台对海面目标或地面目标(离地高度为 0)进行无源定位,通过对误差源的假设和分析,建立了三维空间内的定位模型,采用GDOP(定位精度的几何稀释)来描述最终的定位结果,得出了空基平台自身的定位误差以及红外测量误差对最终定位精度的影响,并进行仿真验证,得到了空基平台三维定位的一些指导性结论。这些结论验证了空基平台无源定位的可行性,为提高空基平台的测量精度提供了依据。
1 定位模型建立
定位模型的建立涉及到如下几个坐标系[2]:地心地固坐标系(ECEF),空基平台NED坐标系,平台载体坐标系,平台天线坐标系。其中,平台载体坐标系是平台 NED坐标系与天线坐标系进行坐标变换的中间系,以平台 NED坐标系为参照测量平台的三个姿态角决定了平台载体坐标系与平台 NED坐标系的变换关系[3]。而ECEF和平台NED坐标系之间的转换关系与平台的经纬度有关[4]。
设观测平台的经纬度分别为 (,)TV=L B 。由此可以确定ECEF到定位平台NED之间的坐标旋转矩阵为

设观测平台飞行过程中的姿态数据为:偏航角θ,纵倾角φ,横倾角γ,设 (,,)TK = θ φ γ 。则平台NED坐标系到天线坐标系的旋转矩阵C2为:

则ECEF坐标系到平台传感器天线坐标系的旋转矩阵为:C=C2*C1。
设平台天线坐标系测得目标的俯仰角和方位角分别为: S =(α, β)T,由此可以得到天线坐标系中所对应的一组方向余弦为 P0=(l0, m0, n0)T。
则 P0= Mαβ= ( cosα s i n β , c osα c o sβ , s in α )T,将其转换为ECEF坐标系中的方向余弦 P =(l, m, n)T得

如图1所示:将地球看成一个位于ECEF坐标系中的椭球,其长、短半轴分别为a,b,地面目标的三维坐标分别为 X =(x, y, z)T,空基平台的三维坐标分别为: X0=(x0, y0, z0)T。则目标的位置可以通过方程组(1)联立求解得出。
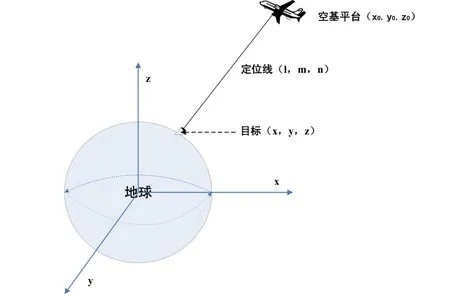
图1 空基平台定位示意图

根据所建立的模型可知,这样的定位问题就转化为解方程的相关问题,以及通过这些方程如何分析定位精度[5]。
设观测平台与地面目标之间的距离为 r,则由公式(1)的第二个方程可得
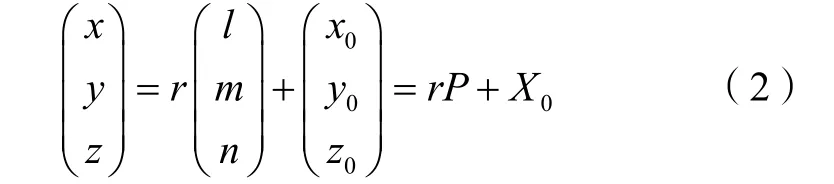
代入式(1)中的第一个方程可得:

从中解出r,从而获得目标的定位坐标。
2 定位精度分析
2.1 定位精度公式推导
下面考虑测量的随机误差来进行精度分析[6]。

对其求全微分后两边取协方差可得:

对式(2)两段进行微分可得到X的协方差矩阵为:

其中,


其中,I为三阶单位矩阵。
2.2 各种测量误差对最终定位结果精度的影响
2.2.1 考虑空基平台的姿态角和经纬度误差
由前面的介绍可知:P是V,K,S的函数,设为

由上式可得:
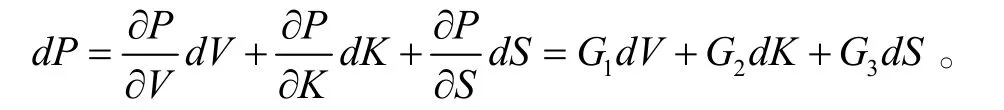
其中,

进一步可以得到:

其中,

将其代入式(5)可得:

其中,
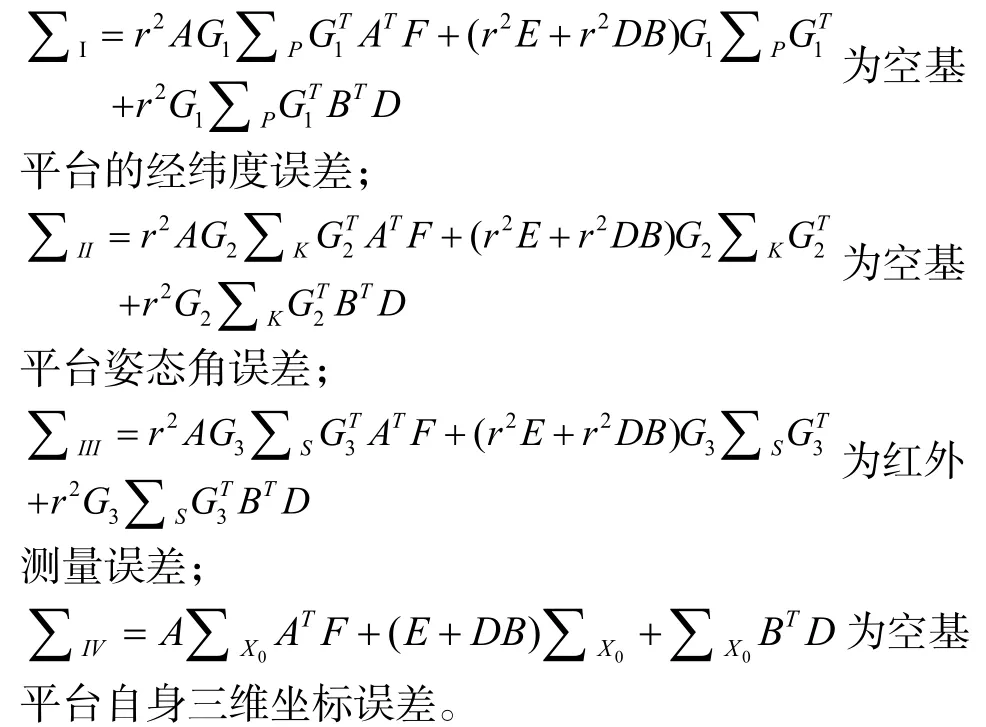
2.2.2只考虑红外测得的方位角,俯仰角误差

其中,

由此可得:

将其代入式(5)可得:

3 仿真结果与分析
假设只考虑红外的测量误差而忽略平台的姿态角误差,在定位站几何布局已定的条件下,分析这种定位系统对不同空间位置上目标的定位误差分布,采用GDOP来描述定位误差,即
在实际应用中,一般都假设红外传感器的测量精度为3mrad,平台自身的定位误差为10m 。若观测平台位于高经纬度地区,设其位置为(W80°, N50°)得到GDOP网格图和等高线图2所示。

若红外传感器的测量精度设为5mrad,其余条件不变,得到的仿真结果如图3所示。
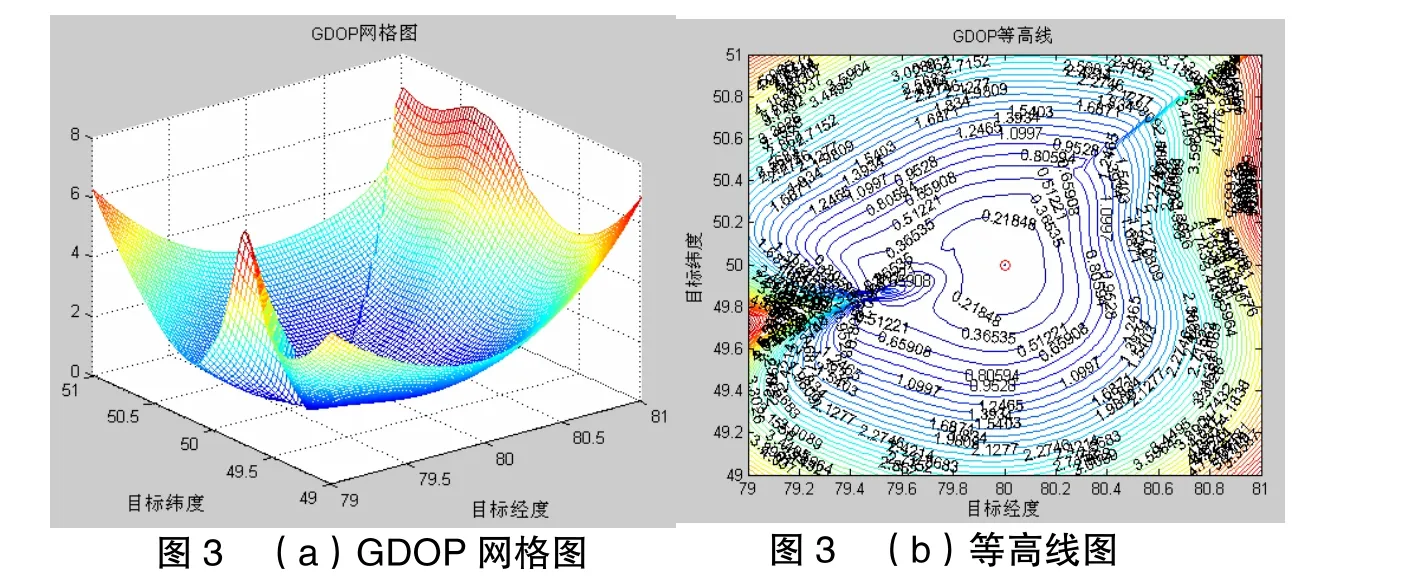
若空基平台位于低经纬度地区,设其位置为(W30°,N20°),其余条件不变,得到的仿真结果如图4所示。
从上述仿真结果可以得出如下一些结论:
1)空基平台具有一定的探测范围,在对其周围一个经纬度内的地面或海面目标进行探测定位时,定位的精度为千米的量级,具有一定的可行性;
2)空基平台自身的定位误差,红外传感器的测量误差都会影响定位精度,其中红外的测量误差具有比较显著的影响,即红外的测量误差是主要的误差源;
3)GDOP的等高线分布近似为椭圆,即空基平台对地面上一系列的目标具有相同的探测精度,而此类目标相对于空基平台具有相同的俯仰角。经过统计计算表明:空基平台对地面或海面目标的探测定位,红外的测量误差中对俯仰角的测量误差是主要误差源;
4)在同样的条件下,经过大量的仿真统计可以得到:观测平台位于高经纬度的探测定位精度要略优于其位于低经纬度的探测定位精度。
4 结束语
通过上述分析可知,当目标位于海面或地表附近时,单平台单次测量就可以实现对目标的三维定位。在已知目标高度的情况下,也可以用这样的方法进行目标定位。当实现了对目标的初次定位以后,进一步可以利用单平台的多次测量信息进行滤波处理,这样可以获得目标位置的精确定位,还可以得到目标的运动相关参数。进一步利用多平台的测量信息不仅可以提高定位精度,还可以对空中目标进行定位。
[1]吴江. 对近空间目标的无源定位探讨[J].Scinece &Technology Information,2008(8):179-180.
[2]李华军,刘新国,黄南发. 纯方位目标运动分析数学模型[J].弹道学报,1994(2):35-41.
[3]邓新蒲,周一宇,万钧力. 机载测角三维无源定位的建模与算法分析[J].国防科技大学学报,2000,22(4):85-89.
[4]孙仲康,周一宇,何黎星. 单多基地有源无源定位技术[M].北京:国防工业出版社,1996.
[5]韦毅,杨万海,李红艳. 红外三维定位精度分析[J].红外技术,2002,24(6):37-40.
[6]谢恺,韩裕生,等. 低轨红外预警星座无源定位精度分析[J].信号处理,2008,24(3):343-348.

