一种基于数学形态学的语音基音轨迹平滑的改进算法

成新民 蒋天发 李祖欣

（湖州师范学院信息与工程学院1） 湖州 313000） （中南民族大学计算机科学学院2） 武汉 430073）

基音的检测提取一直是一个被广泛研究的课题，并提出了各种各样的基音检测算法.然而由于浊音信号的周期性表征极其复杂，无论采用哪一种基音检测算法都可能产生基音检测错误，加之噪音干扰，使求得的基音周期轨迹中有一个或几个基音周期估值偏离了正常轨迹（通常是偏离到正常值的2倍或1／2），这种偏离点称为“野点”.这些脉冲噪声类似于图像中的椒盐噪声，故可以采取平滑技术加以纠正.

目前比较常用的基音平滑方法主要有中值滤波算法和线性平滑算法以及它们的组合.它们有一个共同的缺点是在纠正输入信号中不平滑处样点值的同时，也使附近各样点的值做了修改，从而使信号产生了失真.形态学滤波器作为一种非线性滤波器近年来在数字信号处理领域获得了广泛应用，它基于信号的几何特征，利用预先定义的结构元素（相当于滤波窗）对信号进行匹配，以达到提取信号，抑制噪声的目的.形态学滤波在图像处理领域已经获得了很好的效果.由于基音周期轨迹中的野点类似于图像中的椒盐噪声，并联想到形态学滤波能在有效抑制脉冲噪声的同时较好地保持信号的细节，因此将形态学方法用于基音周期轨迹的平滑是可行的［1－2］.本文就是利用了形态学的概念和方法对基音轨迹进行平滑滤波，在滤波窗口的选取方面进行了一些研究，并针对形态学滤波的特点提出了改进，使算法的精确性进一步提高，复杂性大大降低.

1 形态学运算

数学形态学是以集合论为基础的一种研究方法，它是一种非线性变换.其基本思想是：利用一个称为结构元素的“探针”的移动来收集对象的信息.采用不同的结构元素，可以提取出不同的形状特征，所有的形态学处理都是基于填放结构元素的概念.形态变换一般分为二值形态变换和多值（灰度）形态变换.本文只限于讨论一维离散情况下的多值形态变换.其基本运算包括腐蚀、膨胀、形态开和形态闭.

对于定义在整数集D上的离散函数f（n），它关于结构函数g（n）的基本形态变换定义为：

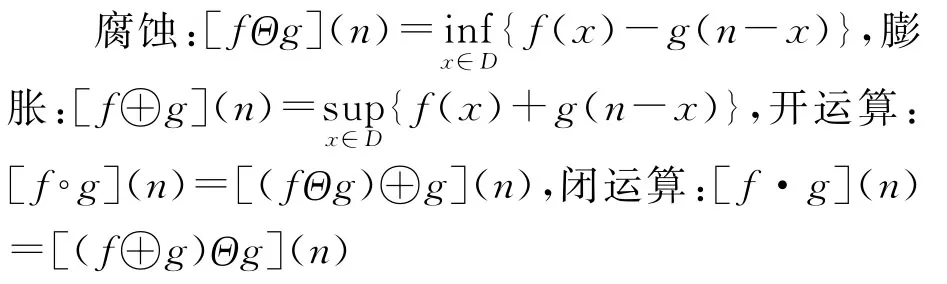
由此不难看出，离散形式的膨胀和腐蚀运算实际上等价于离散函数在结构元素（相当于滑动滤波窗口）中的最大和最小值滤波.开运算和闭运算对信号作用产生的效果不同.开运算可以抑制信号中的峰值〔正脉冲〕噪声，而闭运算可以抑制信号中的低谷（负脉冲）噪声.为了同时去除信号正、负两种脉冲噪声，通常可以采用形态开、闭运算的级联组合形式.

2 结构元素的选择

结构元素的选取是形态学滤波的关键，其形状和大小直接决定了形态运算的效果.所选的结构元素必须既能够有效地抑制噪声，又不损坏信号的细节.而选择结构元素并没有确定的规则和定律，通常要根据信号的几何形态和变化特征进行选择.几种常用的结构元素如图1所示.

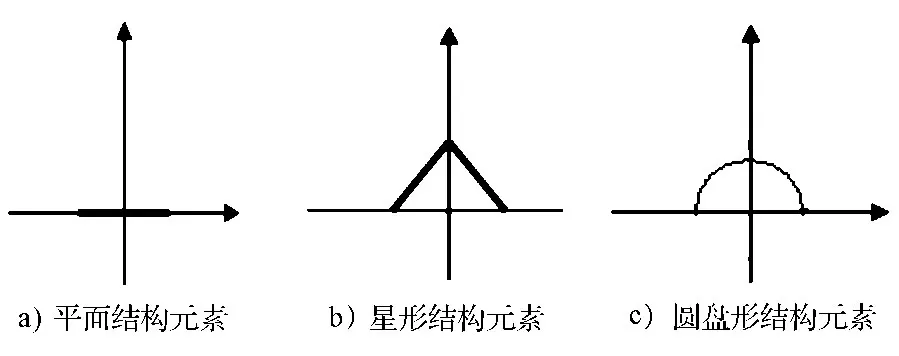
图1 几种常用的结构元素

对于直线段，无疑图1a）所示的平结构元素是最合适的，但是它对于曲线段却通常会引入一些阶梯状变化［3］，破坏了原始图像的几何性状；图1b）所示的星形结构元素通常适合于曲线段，而在直线段部分则会引起一些波动；图1c）所示的圆盘形结构元素是一种折衷.考虑到语音信号的基音轨迹的特点：在短时间内变化比较缓慢，基音轨迹大部分区域比较平滑，但是在某一部分又有可能出现连续的错误点和随机误差，即出现较宽的脉冲噪声，因此本文采用了如图2所示的结构元素.

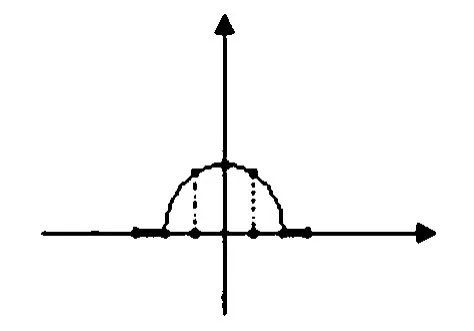
图2 本文采用的结构元素

3 改进的算法

开运算可以抑制正脉冲，闭运算可以抑制负脉冲，开－闭，闭－开的级联形式运算虽然可以同时滤除信号的正、负脉冲噪声，但是存在统计偏移现象.这是由开运算的收缩性和闭运算的扩展性造成的，结果导致开－闭滤波器的输出幅度偏小，而闭－开滤波器的输出幅度偏大.虽然取两者的平均可以消除统计偏移现象［4－5］，但是计算量和复杂性势必很大，因为对信号中的每一个样点都进行了数次开、闭运算，而且多次形态学运算的微小变形累加的结果，仍然会造成信号一定程度上的失真.本文提出的算法是对基本的形态运算加入一些改进，使得形态学的腐蚀和膨胀操作仅作用于那些“野点”，从根本上消除了统计偏移现象，并使算法的复杂性和计算量大大降低，精确性却得到提高.

腐蚀和膨胀运算实际上是离散函数在滑动窗口中的极值运算，这是引起开运算的收缩性和闭运算的扩展性以及开－闭、闭－开的统计偏移的根本原因.可以做这样一种改进：将每次极值运算得到的值作为一个参考值，而不是直接取代被考察的样点的值，将样点值与这个参考值之差与一个阈值相比较，如果差值大于这个阈值，则认为被考察的样点是一个野点，用参考值取代之，否则保留样点的值不变.即对于腐蚀操作，如果

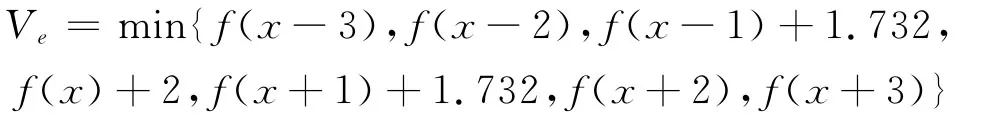
则

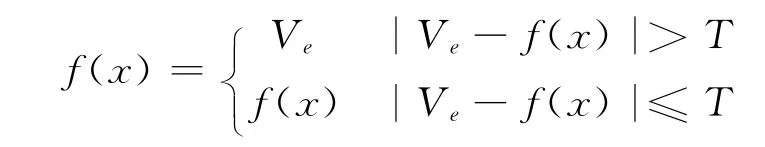
式中：阈值T可以取为对于膨胀操作，如果

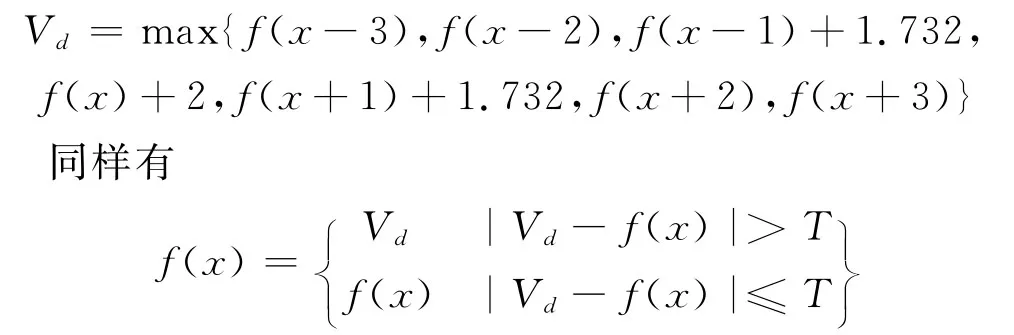
这样，对于一个相同的结构元素，经过一次改进的开运算，正脉冲被消除了，经过一次改进的闭运算，负脉冲被消除了，而那些不是野点的样点值被原封不动的保存了下来.于是整个基音轨迹的平滑过程简化为只需要一次开运算和一次闭运算.

4 实验及结果分析

实验中选择时长各约3～6s的男、女、童音三段语音，分别采用自相关函数（ACF）法、平均幅度差函数（AMDF）法和倒谱（CEP）法对三段语音进行基音检测［6－7］.然后用本文提出的基音轨迹平滑算法对基音轨迹进行平滑，并与采用5点中值滤波得到的平滑结果进行比较.考虑到基音轨迹中相邻帧的频率之差一般不超过10Hz，而隔帧之间的频率差不超过20Hz，因此将本算法中的阈值取为20Hz，并采用前面提到的结构元素进行了实验.实验结果如表1所列.

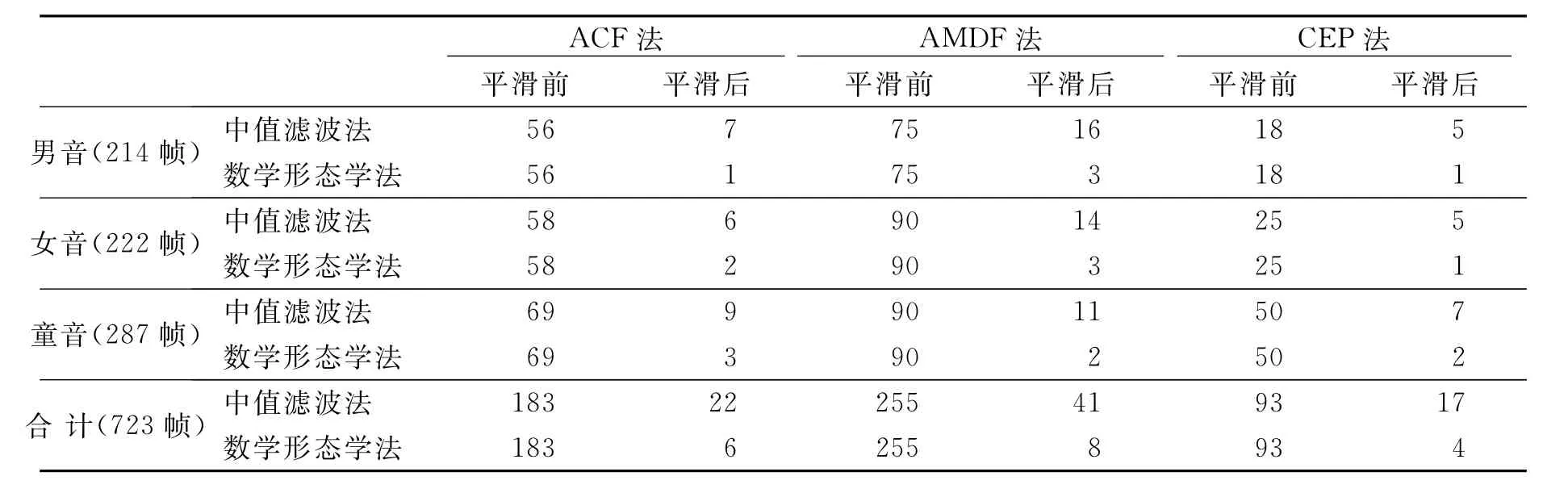
表1 三段语音的基音轨迹平滑前后的检测误差帧数

然后选用一段男声的汉语普通话发音作为实验材料，实验过程框图如图3所示.汉语“你知道这件事”的原始语音信号的时域波形如图4所示.先用自相关法进行基音检测得到图5所示的基音轨迹，然后用本文提出的基音轨迹平滑算法对基音轨迹进行平滑得到图6所示的实验结果，同时采用5点中值滤波得到的图7所示的平滑结果.

同样地，对一段较长的汉语普通话“你们看那只新天鹅……”进行试验，得到如图8～11所示的结果.

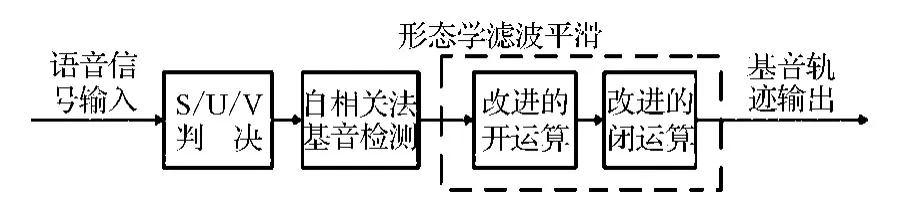
图3 实验过程框图

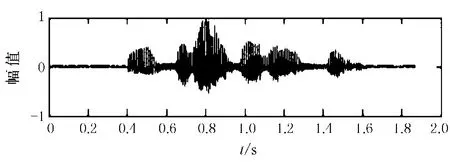
图4 汉语“你知道这件事”原始语音信号的时域波形

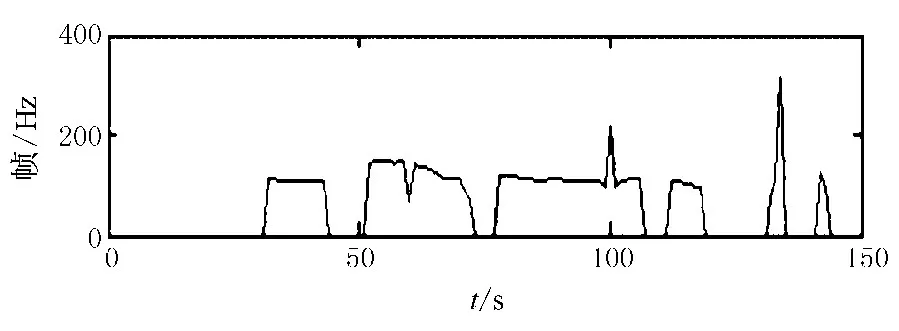
图5 汉语“你知道这件事”未经平滑的基音轨迹

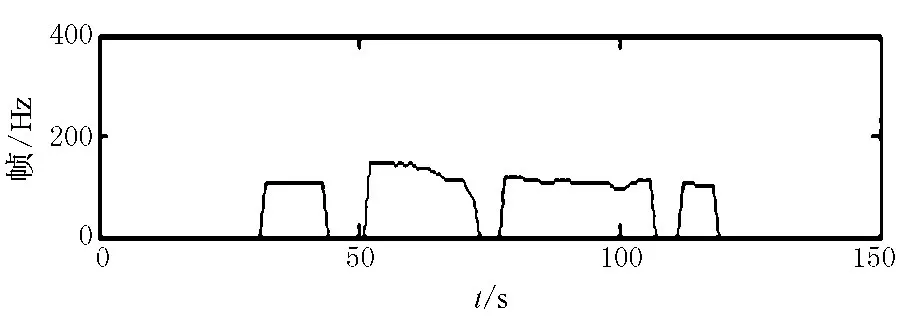
图6 汉语“你知道这件事”经过本文方法平滑的基音轨迹

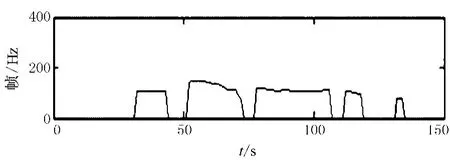
图7 汉语“你知道这件事”经过5点中值滤波平滑的基音轨迹

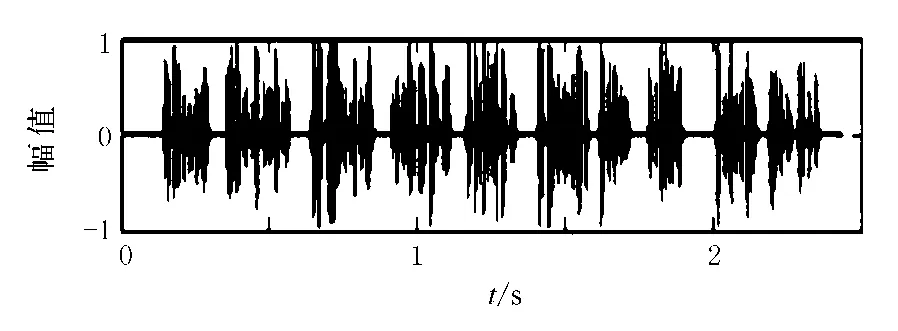
图8 汉语“你们看那只新天鹅……”原始语音信号的时域波形

图9 汉语“你们看那只新天鹅……”未经平滑的基音轨迹

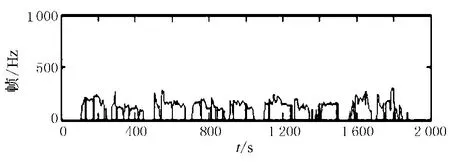
图10 汉语“你们看那只新天鹅……”经过本文方法平滑的基音轨迹

通过实验得到波形，将经本文方法平滑的基音轨迹与经过5点中值滤波平滑的基音轨迹进行比较.可以看出，采用本文提出的方法能够有效地滤除倍频和半频噪声，同时还较好地保持了信号的细节，而且对于连续的错误点和随机误差点具有更好的平滑效果.

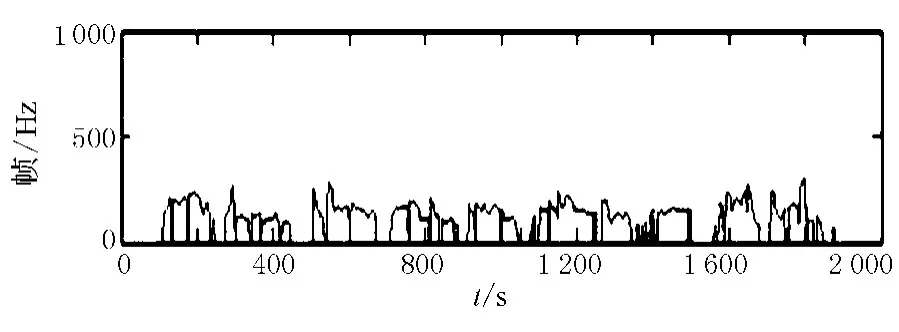
图11 汉语“你们看那只新天鹅……”经过5点中值滤波平滑的基音轨迹

5 结 束 语

形态学滤波是一种非线性滤波方法，原理简单，而且其本身固有的并行性使得运算简单，速度较快.基于对象几何特征的特点决定了形态学方法对滤除脉冲噪声非常有效，无论在二维的图像处理领域还是用于处理一维信号的“野点”.通过选取不同形状和大小的结构元素，可以实现不同的平滑效果.传统的中值滤波平滑是一种强制性平滑，可能平滑掉信号中的某些固有突变，破坏信号的细节特征，形态学运算实际上是极值运算，也可能存在这个问题.而本文提出的方法则有效地解决了这个问题.

［1］江太辉.一种改进的语音基频轮廓提取算法［J］.五邑大学学报，2002，16（2）：27－33.

［2］郭景峰，申光宪，郑绳楦，等.数学形态学在数字滤波中的应用研究［J］.机械工程学报，2002，38（10）：144－147.

［3］赵晓群，王光艳.汉语语音基音轨迹的形态学滤波和平滑［J］.信号处理，2003，19（4）：354－357.

［4］王钧铭，赵 力.一种基于数学形态学的车牌图像分割方法［J］.电视技术，2007，31（10）：84－86.

［5］陈 燕，谭玉敏，宋新山，等.基于遥感图像的地学信息单元特征提取与识别［J］.武汉理工大学学报：交通科学与工程版，2008，32（6）：1021－1024.

［6］Yu P T，Some representation properties of stack filters［J］.IEEE Transactions on Signal Processing，1992，40（9）：2261－2266.

［7］Gonzalo R A.Statistical threshold decomposition for recursive and no recursive median filters［J］.IEEE Transactions on Information theory，1986，32（2）：243－253.