零件直线度误差虚拟检测系统研究

续永刚，向立明，高国生

（1. 石家庄职业技术学院 机电系，石家庄 050081；2. 石家庄铁道学院 研究生分院，石家庄 050043；3. 石家庄铁道学院 科技处，石家庄 050043）

0 引言

随着近代科学技术的迅速发展和生产水平的不断提高，机加工工业的制造精度和与之相应的检验测量器具都有了很大程度的提高和完善。有关形位误差的评定方法、评定理论、解算方法等问题的研究，已成为计量学领域研究的热点[1]。

机械零件的直线度误差对机械产品的质量有很大影响。准确地求得零件直线度与圆度误差数值，对保证和提高机械产品的质量十分重要。目前，测量轴线直线度误差可以用智能形位误差测量仪，但这种仪器成本高且不能进行功能扩展。

虚拟仪器的核心是利用计算机所具有的高速计算吞吐能力和计算机环境下丰富的系统资源，将原来用硬件设备完成的功能转化为用计算机软件来解决，这就是所谓“软件就是仪器”的测量理念。由于采用了软件设计技术，大大降低了测量系统的成本，同时对于测量信号的处理更具灵活性。虚拟仪器突破了传统智能化形位误差测量仪在数据处理、显示、传输、存储等方面的限制，用户可方便地进行功能扩展[2]。

本文要研究开发一个自动检测零件形位误差（直线度）的虚拟智能检测系统，使机械零件形位误差的检测成本低、速度快及精度高。该系统用到美国国家仪器公司开发的LabVIEW软件。

1 直线度误差的评定

直线度误差是指实际直线对其理想直线的变动量，理想直线的位置应符合最小条件。与直线度公差带相对应，直线度误差分为给定平面内、给定方向和任意方向的直线度误差等三种形式。在满足被测零件功能要求的前提下，直线度误差值可以选用不同的评定方法来确定。

1.1 给定平面内的直线度误差评定

1.1.1 最小包容区域法

图1 最小包容区域

根据给定平面内直线度公差带的形状，由两条平行直线包容实际被测直线S时，成“高—低—高”或“低—高—低”三极点相间接触，则这两条平行直线之间的区域就是最小包容区域U，如图1所示。这称为给定平面内直线度误差最小区域判别准则。它们之间的宽度 即为符合定义的误差值。

在本方法中,本文采用“高—低—高”三极点相接触的方法。本文测试所用的数据来自参考文献[3]。该文献中所用数据取自三坐标实测结果，在计算中发现，文献的MATLAB求解程序与三坐标机求解结果基本上没有差异，本文用LabVIEW软件编程求解程序与该文献的求解结果也基本上没有差异。其计算结果如表1所示。

表1 最小区域法计算结果

本文用LabVIEW软件编程所得结果及可视图如图2所示。

图2 最小区域法(LabVIEW编程)

1.1.2 最小二乘法

如图3所示，最小二乘中线lLS是一条穿过实际被测直线的理想直线。它所处的位置使实际被测直线上各点至它的距离的平方之和为最小。以该理想直线作为评定基准，取测得各点相对于它的偏离值中的最大偏离值hmax与最小偏离值hmin之差fLS作为直线度误差值。在它上面的测点的偏离值取正值；在它下面的测点的偏离值取负值，fLS=hmax-hmin。

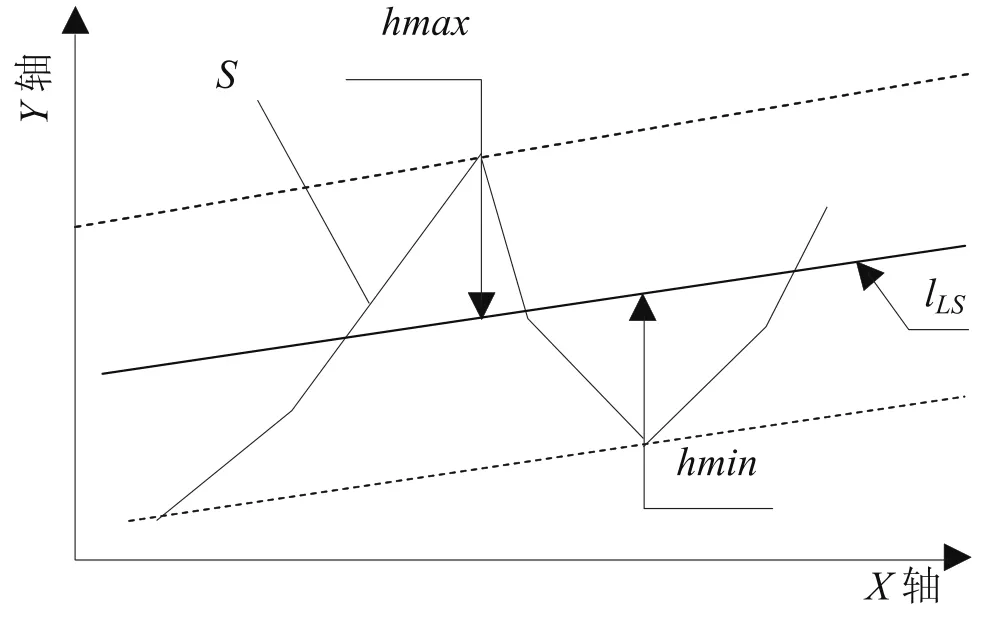
图3 最小二乘法

在本法中就是要通过将采集到的原始数据用最小二乘法拟合成一基准直线。该法所采用的数据与最小区域法一样，其计算结果如表2所示。

表2 最小二乘法计算结果

本文用LabVIEW编程求解得到的结果及可视图如图4所示。

图4 最小二乘法(LabVIEW编程)

1.1.3 两端点连线法

如图5所示，以实际被测直线S的首、末两点B和E的连线lBE作为评定基准，取测得各点相对于它的偏离值中的最大偏离值hmax与最小偏离值hmin之差fBE作为直线度误差值。在它上面的测点的偏离值取正值；在它下面的偏离值取负值，即fBE=hmax-hmin。

图5 两端点连线法

两端点连线法就是将采集到的原始数据中的首末两点连成一条直线作为评定基准。本法所用数据与前两种方法一样，其计算结果如表3所示。

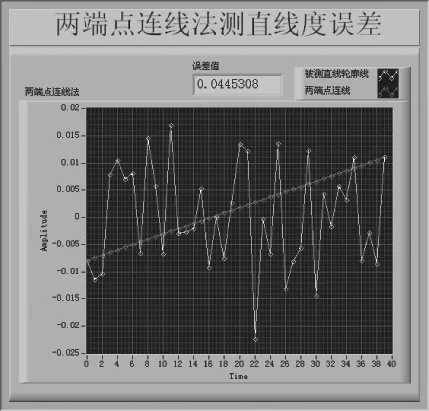
图6 两端点连线法(LabVIEW编程)

表3 两端点连线法计算结果

本文用LabVIEW编程求解得到的结果及可视图如图6所示。

1.2 任意方向的直线度误差评定

最小二乘中线法。如图7所示，用轴线平行于实际被测轴线S的最小二乘中线lLS的圆柱面包容该实际被测轴线时，取其中具有最小直径的圆柱面的直径fLS作为误差值。具有最小直径的圆柱面与实际被测轴线的接触有两点接触和三点接触两种形式，本文采用两点接触形式。

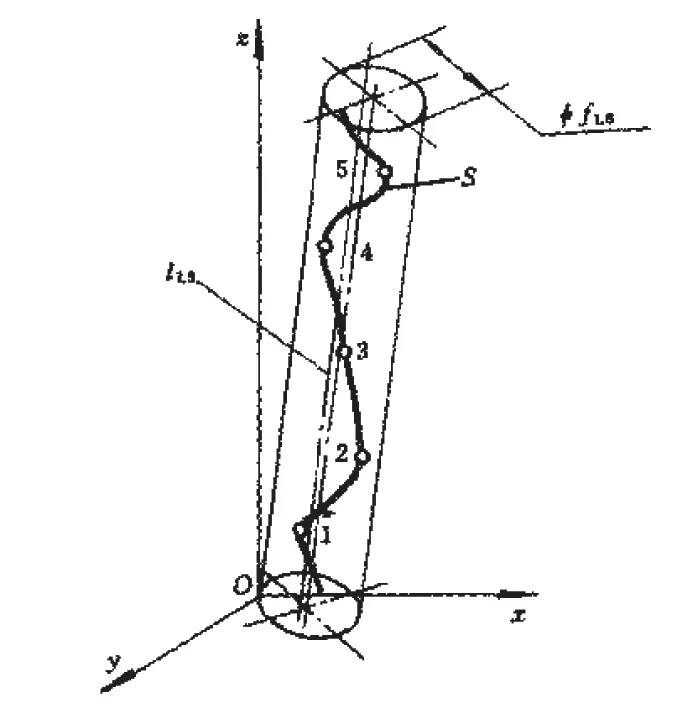
图7 最小二乘中线

两点接触形式是指实际被测轴线上各测点在垂直于最小二乘中线的平面上的投影，由以相距最远两点的连线为直径的圆所包容。根据被测轴线的分段数n (即测点数日为n+1)和各测点的坐标(xi，yi，zi)，按最小二乘原理求出该被测轴线的最小二乘中线lLS的方程系数a，b，c，g：

式(1)中，坐标值xi，yi和zi的下角i为测点序号，i=0,1,2,…,n。然后由其余各测点的坐标(xi，yi，zi)分别求出它们至最小二乘中线lLS的距离hi：

找出hi中的最大值hmax，判断以2hmax为直径的圆柱面符合最小直径包容圆柱面的要求与否。若不符合，则按一定的优化方法改变a和b的数值，并重复上述计算，—直到符合最小直径包容圆柱面的要求为止。最小直径包容圆柱面的直径即为被测轴线的直线度误差值。测试所用的数据也来自参考文献[3]。本文用LabVIEW软件编程求解程序与参考文献[3]求解结果基本上没有差异。其计算结果如表4所示。

表4 最小二乘法计算结果

本文用LabVIEW编程所得可视图及计算结果如图8所示。

2 结论

本文以LabVIEW软件为平台，充分利用该软件的特点，开发出了对零件形位误差进行评定的软件包，并使用他人的实验数据对评定软件进行了验证，结果表明：系统具有精度高、速度快、成本低和适合现场使用和维护等特点。

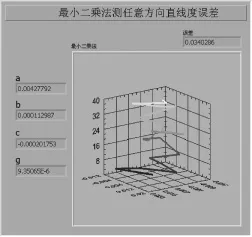
图8 最小二乘法可视图及计算结果(LabVIEW编程)

本文所开发的测试系统对直线度误差能做出准确的分析和正确的评价，其研究结论具有很强的实用价值，对相关的研究提出了一种研究思路，并具有一定的指导意义。

[1] 熊有能.精密测量的数学方法[M].北京:中国计量出版1989,12-13.

[2] 陈立杰,田文元,张镭.轴线直线度误差虚拟测量仪的研制[J].东北大学学报(自然科学版),2007,28(2),250-253.

[3] 陈永鹏.基于MATLAB优化工具箱的机械产品形状误差评定系统研究[D].四川:四川大学,2003.