基于成长型神经网络以线段为基元的曲线重建

王世东 ， 张佑生， 王焕宝

（1. 中国科学技术大学火灾科学国家重点实验室，安徽 合肥 230026;2. 安徽建筑工业学院信息网络中心，安徽 合肥 230022;3. 安徽三联学院计算机科学与技术系，安徽 合肥 230601）

逆向工程的主要任务是由物理模型重建出几何表示模型，通常包含4个步骤：数据采集、数据预处理、曲面拟合和CAD模型重建。其中,曲面拟合和CAD模型重建是逆向工程中最为重要的部分[1]。Alrashdan将逆向工程分成三个主要步骤：零件数字化，特征提取，CAD建模。其中，特征提取是通过点云分块以及表面特征识别来完成的[2-3]。近年来，在逆向工程中，对特征提取问题的研究比较活跃。Géza Kós等对等半径过渡特征曲面提取问题进行了研究[4]。Lu等对等/变半径过渡曲面特征提取进行了研究[5]。文献[4-5]只能针对比较规则简单特征的提取。Ke等深入研究了点云切片算法和拉伸面特征的提取[6-7]，能高效地构造点云有序组织形式和提取如拉伸面、旋转面等复杂曲面特征。随着神经网络技术的广泛应用，使用神经网络实现特征提取逐渐成为一个热门研究课题。Jun等研究了基于神经网络的棱柱特征[8]，如边、孔等的识别。Xiao等提出使用正交神经网络重建曲线[9]，但当点云具有明显角点和较多噪声数据时，文献[8-9]算法重建效果并不理想。

IVRISSIMTZIS等提出使用成长型神经网络以三角面片为基元重建实体模型[10]。在此基础上，本文提出基于成长型神经网络以线段为基元的曲线重建算法。给定某一曲线的散乱点集和一个初始折线，使用成长型神经网络优化折线上顶点的位置，使折线更好地逼近散乱点；持续分裂折线上活动性强的顶点和删除活动性最弱的顶点，使顶点的分布更符合散乱点数据的概率分布。算法使折线上的顶点不断增加，折线不断成长，直至达到要求的重建效果。实验结果表明，该算法的计算速度不受输入数据量大小的影响，非常适合大规模散乱点集和含噪声数据的学习，能够取得良好的曲线重建效果。

1 曲线重建原理

1.1 成长型神经网络

成长型神经网络（Growing Cell Structures,下文简称 GCS网络）属于自组织特征映射神经网络（Self-Organizing Feature Map，下文简称SOM网络）。SOM网络是芬兰学者Kohonen在1980年根据生理学规律提出的。它是一种具有侧向联想能力的两层网络，能把输入层含m维的向量特征映射到一维或二维拓扑空间中，如图1所示，该网络输入为m维向量，输出为一维拓扑神经元。SOM 引入变化邻域概念来模拟生物神经网络中的侧抑制现象：生物神经元接受刺激并进行竞争产生获胜神经元，该神经元和它邻域的神经元得到加强，邻域之外的神经元由于距离它较远而受到抑制，这样就可实现网络的自组织特性。

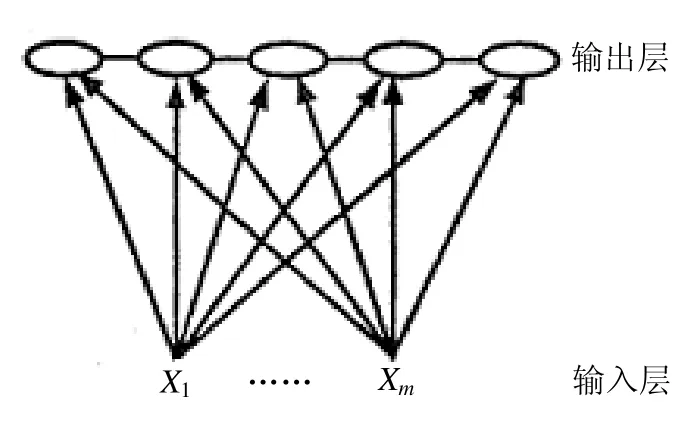
图1 一维输出的SOM模型

GCS网络是一种特殊的SOM网络，它能够增量生长。该网络在学习输入向量的过程中，根据神经元竞争获胜次数的多少确定它们活动性的强弱，分裂活动性强的神经元，删除活动性最弱的神经元，使网络更好地体现输入向量的内在特征。

1.2 曲线重建模型

基于 GCS网络曲线重建模型的输入向量为散乱点 X，输出层 k个神经元为折线上的顶点,神经元的权向量Wj=[wj1,wj2, wj3]T, j=1,2,…, k为折线上顶点vj的坐标。在学习过程中，获取与散乱点 X欧氏距离最小的折线顶点作为竞争获胜顶点vw，将它和它的拓扑邻域内的顶点向该散乱点移动。通过这种移动，使顶点的位置更逼近散乱点。该过程如图2所示。

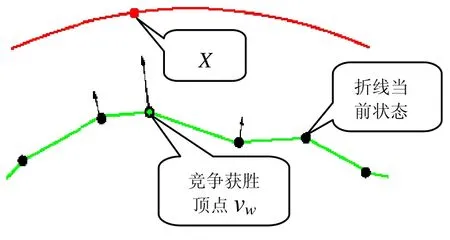
图2 折线顶点的学习过程

折线上每一顶点有一计数器，其值的大小反映该顶点活动性的强弱。在学习每一散乱点时，更新所有顶点计数器值，使竞争获胜顶点和它拓扑邻域内的顶点计数器值增大，其它顶点计数器值减小。学习指定个数散乱点后，分裂活动性强的顶点，删除活动性最弱的顶点。分裂顶点和删除顶点过程如图3所示。图3(b)中，顶点E分裂后新增一顶点F，图3(c)中，C点被删除后，相邻两顶点相连形成一条新边。模型通过对散乱点的学习，持续分裂活动性强的顶点和删除活动性最弱的顶点，使折线上顶点个数不断增长并愈来愈逼近实际曲线，从而实现曲线重建。

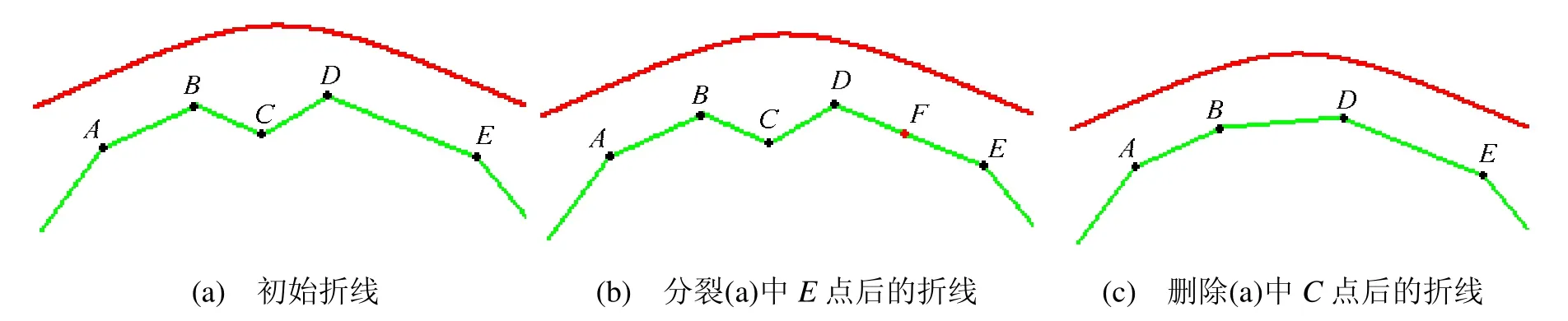
图3 顶点的分裂和删除

2 曲线重建算法

使用成长型神经网络以线段为基元的曲线重建算法的基本思路是：从散乱点集中随机取出一散乱点，在折线上找出与该点欧氏距离最小的顶点作为竞争获胜顶点，将它向该散乱点移动一定距离；同时调整其拓扑邻域内的各顶点的位置和所有顶点计数器值，在学习过程中，不断分裂活动性强的顶点，删除活动性最弱的顶点。直至满足预定的结束条件。

如上所述，折线用L表示，折线上顶点v的集合用V表示，算法的步骤如下：

（1）取初始折线L，设散乱点集P中的点数为 N，令 n＝0表示初始迭代次数，初始学习速率为η(n)<1。

（2）从P中随机选取一散乱点X。

（3）在 V中找到与散乱点 X欧氏距离最小的顶点vw，如式（1）所示

（4）更新vw和它拓扑邻域内顶点的位置。vw的新位置是它原来位置和采样点X的位置的线性组合。如式（2）所示

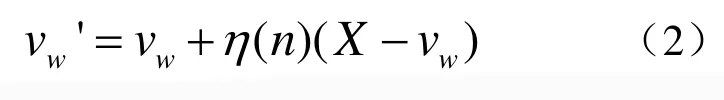
vw拓扑邻域内其他顶点位置的更新，如式（3）所示

式(3)中，λ(n)值如式（4）所示

式中 t为5～40较合适。

（5）更新学习速率η(n)，如式(5)所示

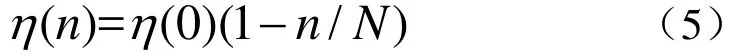
（6）更新L中所有顶点的计数器值，竞争获胜顶点的计数器值的更新按式（6）进行

其它顶点计数器值的更新按式（7）进行

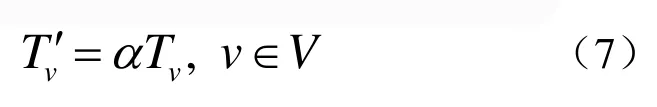
式中 α为小于1的正数。

（7）上述(2)～(6)步迭代若干次，分裂具有最高计数器值的顶点，如图3(b)所示。折线L的弹性能量[10]如式（8）所示

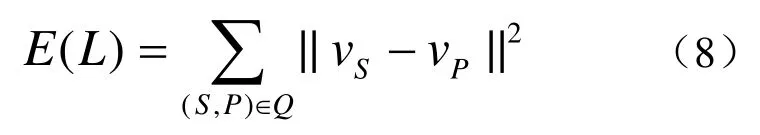
式中 Q为折线上边的集合。新增顶点的位置应使折线的弹性能量最小化。通过式（8）可求出折线新增顶点的位置应为分裂顶点较长邻接边的1/2处为宜。以图3(b)为例，则F点坐标如式（9）所示

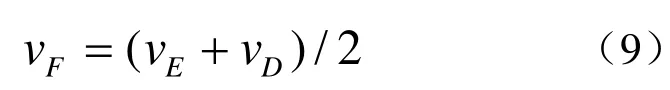
令式Z(F)=DF2+EF2，即求顶点F相邻边长度的平方和。则顶点分裂后E点和F点计数器值如式（10）和式（11）所示

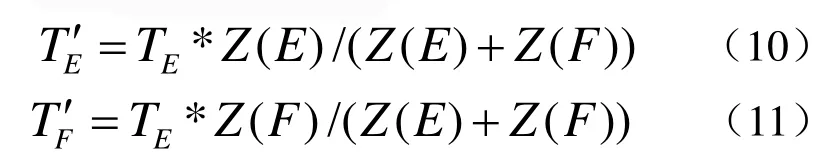
（8）上述(2)～(7)步迭代若干次，删除L中计数器值最小的一顶点。删除该顶点后，连接它拓扑邻域的两顶点，如图3(c)所示，拓扑邻域内两顶点计数器值保持不变。

上述(2)～(8)的过程重复迭代，直至达到预设最大迭代次数为止。

3 实验结果与分析

作者在Pentium 4-2.5GHz 处理器、1024M内存微机平台上，用VC6.0和OpenGL实现了本算法，用它对某些曲线的散乱数据点集训练并进行重建，取得良好效果。图4为的散乱点集。

图5为 y =s inx, x ∈ [ 0,2π]散乱点集的重建过程，共使用 8740个散乱点。图5(a)为包含 2个顶点的初始折线。

图4 y=sinx的散乱点集

图5 sinx曲线重建过程

表1给出了y=sinx重建过程中的相关参数。

表1 y=sinx重建相关参数

图6为古代一刀具轮廓的散乱点集。

图6 刀具轮廓散乱点集

图 7为刀具散乱点集的重建过程，共使用6480个散乱点。图7 (a)为包含3个顶点的初始折线。

图7 刀具轮廓重建过程

表2给出了刀具重建过程中的相关参数。

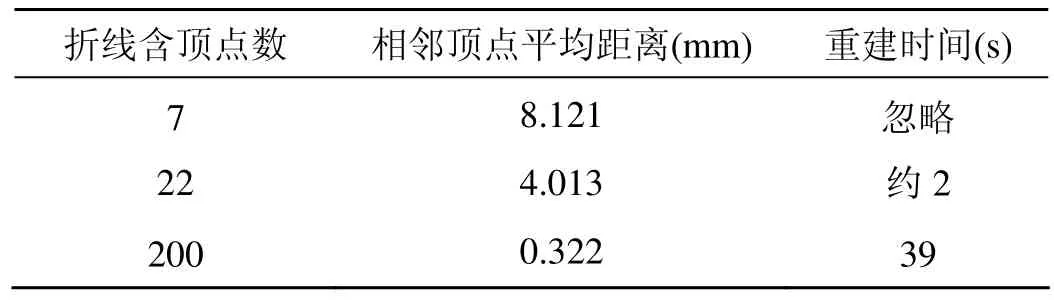
表2 刀具重建相关参数

从图5和图7可看出，重建结果几乎不受噪声数据的影响，有非常好的重建效果。从表1和表2中可看出，曲线重建后，顶点间距已达到常用显示设备像素间距水平，图5折线上顶点投影到原始曲线的平均距离误差几乎为零，顶点对原始曲线有很好的拟合；输入数据量与重建时间近似成线性关系，重建过程所需时间短，重建速度较快。

4 结束语

本文提出基于成长型神经网络以线段为基元的曲线重建算法，使用该算法优化折线上顶点的位置，使折线更好地逼近散乱点；持续分裂折线上活动性强的顶点和删除活动性最弱的顶点，使顶点的分布更符合散乱点数据的概率分布。实验结果表明该算法十分有效，且具有重建速度快，不受散乱点数据量大小影响的特点。

[1]Várady Tamás, Ralph R R, Jordan Coxf. Reverse engineering of geometric models-an introduction [J].Computer-Aided Design, 1997, 29(4): 255-268.

[2]Alrashdan Abdalla, Motavalli Saeid, Fallah Behrooz.Automatic segmentation of digitized data for reverse engineering applications [J]. IIE Transactions, 2000,32(1): 59-69.

[3]Huang Jianbing, Menq Chia-hsiang. Automatic data segmentation for geometric feature extraction from unorganized 3-D coordinate points [J]. IEEE Transactions on Robotics and Automation, 2001, 17(3):268-279.

[4]Géza Kós, Martin R R, Várady Tamás. Methods to recover constant radius rolling ball blends in reverse engineering [J]. Computer Aided Geometric Deign,2000, 17(2): 127-160.

[5]Lu Zhen, Ke Yinglin, Sun Qing, et al. Extraction of blend body feature in reverse engineering [J]. Chinese Journal of Mechanical Engineering, 2003, 16(3):248-251.

[6]Ke Yinglin, Wang qing. Research on point cloud slicing technique in reverse engineering [J]. Journal of Computer–Aided Design & Computer Graphics, 2005,17(8): 1798-1802.

[7]Ke Yinglin, Li An. Extruded surface extraction base on unorganized point cloud in reverse engineering [J].Journal of Computer–Aided Design & Computer Graphics, 2005, 17(6): 1329-1334.

[8]Jun Y, Raja V, Park S. Geometric feature recognition for reverse engineering using neural networks [J].International Journal of Advanced Manufacturing Technology, 2001, 17(6): 462-470.

[9]Xiao Shaoyong, Jin Shigang, Shi Wenjun. Curve reconstruction based on orthogonal neural network [J].Journal of Image and Graphics, 2000, 5(1): 62-65.

[10]IVRISSIMTZIS I P, JEONG W-K, SEIDEL H-P.Using growing cell structures for surface reconstruction [DB/OL]. http://csdl2.computer.org/comp/proceedings/smi/2003/1845/00/18450288.pdf,2005-10-7.