风电场风速时间序列峰度研究

陈 昊，王玉荣

（1.南京供电公司，江苏 南京210008；2.东南大学电气工程学院，江苏 南京210096）

风能清洁无污染，在全球范围来看风力发电是增长最快的可再生能源发电方式。风电近年来在我国的发展十分迅猛，到2020年我国风电的装机容量将达到30 GW[1]。国内外各种与风电相关的研究方兴未艾，推动着风电技术的发展。风电场短期风速时间序列的研究对于预测风电出力有重要意义。然而由于影响风速变化的因素很多（如温度、气压梯度、地表粗糙度等），导致风速规律性较差，波动变化较剧烈，预测难度较大。目前，风速预测的常见方法主要有持续预测法，时间序列法[2]、人工神经网络法[3]、卡尔曼滤波法[4]等。GARCH模型是刻画时间序列波动性的重要模型，近年在电力领域的应用不断拓展[5]。文献[6]分析了风速时间序列的自回归条件异方差（ARCH）效应，建立了基于ARCH的风速预测模型。目前GARCH风速模型主要集中在应用层面，进一步讨论还有待深入展开。Bai,Russell,Tiao研究了GARCH模型的峰度[7]，并提出用于峰度分析的定理（简称BRT定理），但该定理峰度的定义采用了Excess kurtosis的形式。按照电力系统文献更常用的峰度定义u4/σ4重新推导了BRT定理，并使用该定理对GARCH风速模型进行了一些理论层面的讨论，并结合实际风速数据完成了GARCH风速模型的峰度分析。

1 GARCH模型与峰度研究

1.1 GARCH模型简介

Engle（1982）开创性地提出了ARCH模型，拉开了波动性研究序幕。Bollerselev（1986）提出ARCH的重要推广形式GARCH（p，q）模型[8]，如下。

条件均值方程：

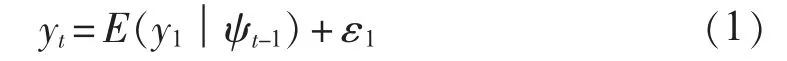
条件方差方程：

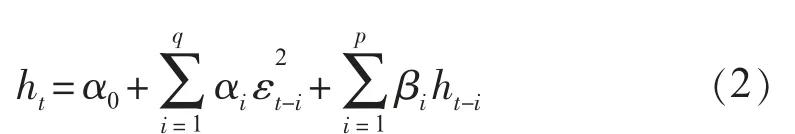
GARCH模型的另一种重要的表达形式是GARCH的ARMA（r，q）表示。这种表达形式对于峰度分析十分重要。记，GARCH模型的条件方差方程变形为：

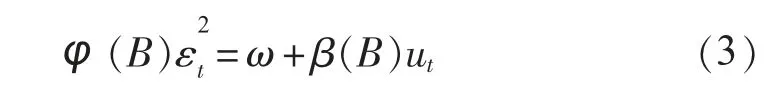
1.2 峰度分析的定理及证明

GARCH模型的自身结构和条件峰度都可以带来高峰厚尾，两者对模型整体峰度分别具有何种影响，对于理解和使用GARCH模型有重要意义。Bai等人定量研究了这一问题，并提出了BTR定理。

文献[7]对以ARMA形式表示的GARCH模型附加2条假设：

（1）多项式φ（B）的根在单位圆外；

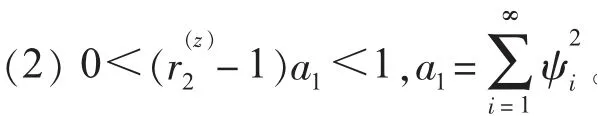
式中：ψi取自

通过这2条假设，保证了E（ut）=0，方差有界且不相关，同时保证了的弱平稳性。

记Zt的峰度为K（z），称εt的峰度为整体峰度，如果峰度存在，记为K（ε）。如果Zt服从高斯分布，K（z）=3，称由式（1，2）定义的随机过程为正态GARCH过程，称高斯GARCH过程的峰度为GARCH峰度，如果峰度存在，记为K（GARCH）。应注意峰度的定义采用了异于BTR的形式，将基于该定义的BTR定理改写成如下形式。

定理1：如果εt服从GARCH（p，q）过程，满足假设1，假设2，则有

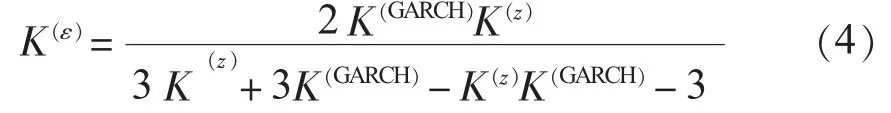
下面给出定理1的证明。

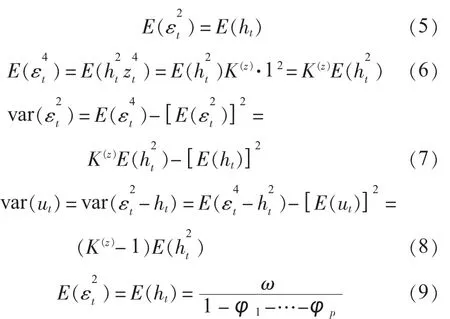
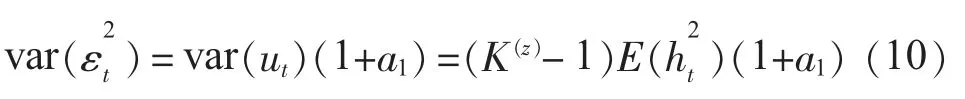
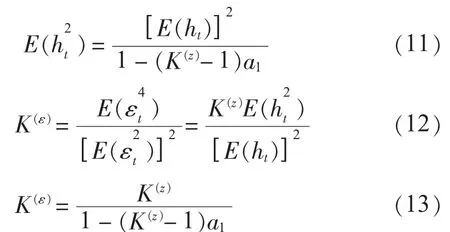
由K（GARCH）的定义，令K（z）=3，有：

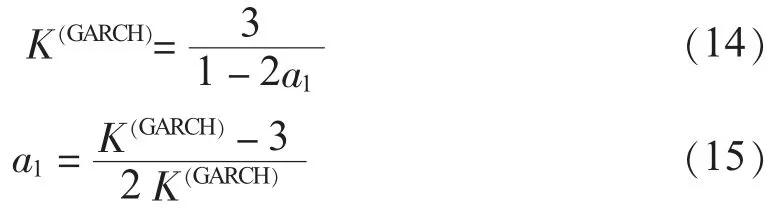
将式（15）代入式（14），则有：

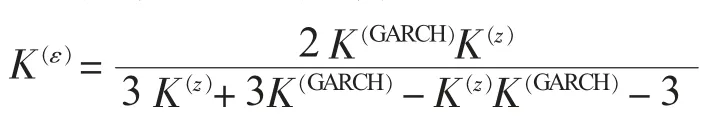
定理1可方便用于εt的峰度分析，可以从整体峰度中分解出哪些是由GARCH模型本身造成的高峰度，哪些是由条件分布造成的高峰度。

1.3 GARCH模型的条件分布

峰度为K（z）允许有很多种变化，条件分布zt的形式自然也不限于高斯分布[9]。这里介绍算例部分使用的2种非高斯分布。

（1）拉普拉斯分布

拉普拉斯分布又名双指数分布，密度函数形如：

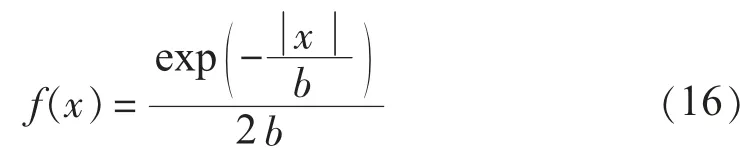
（2）广义误差分布（GED）

GED是一种概括性较强的分布，应用范围广泛。标准GED函数形如：

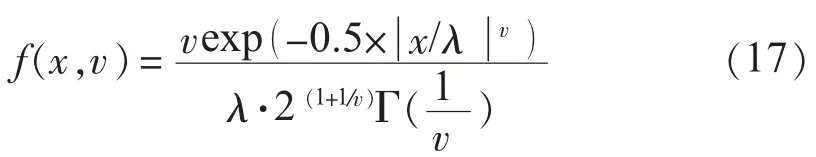
2 算例分析

2.1 数据及初步分析

文中基于某风电场测风点（2 kW机组）2007年连续12 d、每天96点的风速实测数据建立模型，样本空间共有1 152个数据点。

计算风速数据的统计特征，可得均值为0.480，标准差为0.747，偏度为2.411，峰度Ksmpl=9.374。易见，风速数据具有很高的峰度，使用具有描述高峰厚尾效应的GARCH模型是有合理性的。

2.2 ARMA-GARCH模型的建立

采用统计经典方法分析数据序列，首先使用ADF检验和PP检验风速时间序列的平稳性。2种检验一致拒绝了单位根假设，从而表明建模的平稳性前提是满足的。

自回归移动平均（ARMA）结构经常用于描述风速时间序列的相依关系。使用ARMA作为条件均值方程，条件方差方程采用GARCH（1，1）。

分析风速时间序列自相关、偏相关函数，建立模型可行阶数的备择模型集，使用极大似然估计（MLE）获得所有备择模型的参数估计。通过权衡所有备择ARMA的SIC，兼顾ARCH过程的严平稳性等约束条件，最终将模型阶数厘定为ARMA（3，3）-GARCH（1，1）。应注意此时的模型是基于条件正态假设的，故将该模型简记作GARCH-Gaussian模型。

进一步GARCH模型推广非高斯形式（拉普拉斯分布，GED），分别简记为GARCH-L，GARCH-GED模型。考虑到可能存在的厚尾效应，GED厚尾参数取1.2。

同样使用MLE方法获得GARCH-L和GARCH-GED的参数估计，通过BHHH算法控制迭代过程。条件方差方程参数见表1。

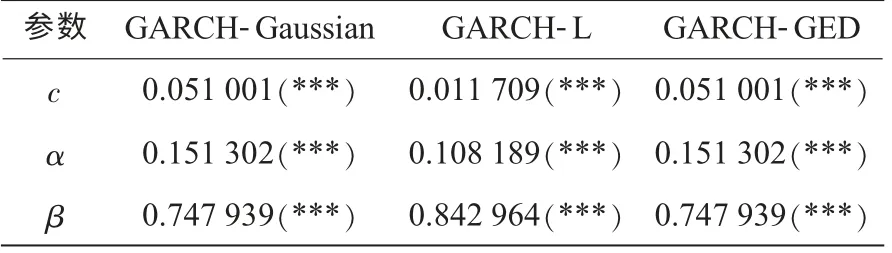
表1 GARCH模型的参数估计

3种GARCH模型的所有参数均显著，且符合GARCH模型平稳性条件，其他统计指标亦良好。峰度分析以这3种模型为基础。

2.3 GARCH模型的峰度分析

借助2.2节证明的定理1，可以对风电场风速时间序列进行峰度分析。

2.3.1 模型的K（GARCH）计算

据文献[8]可知，对于一个GARCH（1，1）模型有

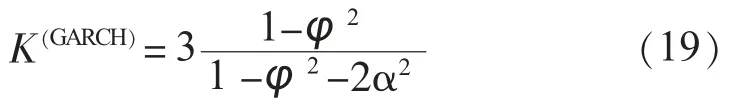
可以分别根据表1中的参数计算出3种模型的K（GARCH）（见表2）。

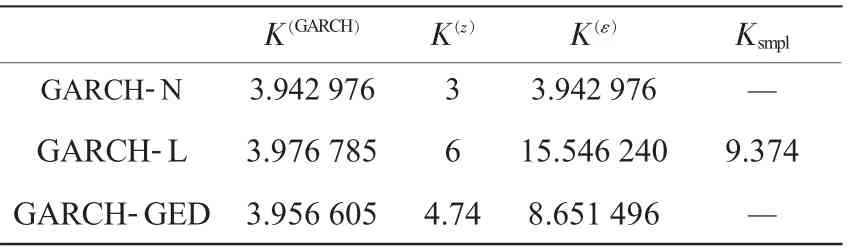
表2 GARCH模型的峰度比较

2.3.2 整体峰度K（ε）计算

正态和拉普拉斯分布的K（z）为常数，GED的K（z）可由式（18）计算。使用定理1可方便求得各模型的整体峰度K（ε），并与样本实际峰度相比较，见表2。

由表2可得出以下几点结论。

（1）GARCH模型自身的结构可以产生高峰厚尾，即使z为正态分布，整体峰度K（ε）亦可以出现高于正态的峰度。

（2）拉普拉斯分布的K（z）较高，最终整体峰度K（ε）也最高。在K（GARCH）相近情况下，K（z）的高下对整体峰度有较大影响。

同时应该注意到，K（GARCH）的变化受模型参数的约束，控制K（GARCH）相对困难，而z的选择余地较大，通过K（z）对K（ε）进行调节相对方便。

（3）本算例的3种模型中，GARCH-N模型的整体峰度不足，GARCH-L模型则超过。相对比较，GARCH-GED刻画的和数据的实际分布Ksmpl最为接近。

（4）GARCH模型条件分布类型及分布参数的选择问题常常困扰着研究者，一般采用样本外预测效果来确定。通过对GARCH模型的峰度分析，寻找能使与Ksmpl最匹配的条件分布，可以在参数估计完成的同时就能就分布选型为研究者提供参考，尤其适合于样本外预测结果获取成本高的情形。

3 结束语

以往对风速的研究讨论均值方差者居多，高阶矩的讨论相对较少。从文中的研究来看，高峰度正是风速固有的重要特性之一。对风速时间序列峰度的研究对更好地理解风速时间序列是有益的。

文章根据电力系统文献常见峰度定义，给出了BTR定理的新形式，并证明了该定理，为风速时间序列峰度分析在理论上提供了方便。

另外，算例分析中采用不同分布GARCH模型模拟了风速数据的峰度，并做出比较，为GARCH风速预测模型条件分布的选择提供了一种可行方案。

[1]李俊峰，时璟丽，施鹏飞，等.风力12在中国[M].北京：化学工业出版社，2005.

[2]丁 明，张立军，吴义纯.基于时间序列分析的风电场风速预测模型[J].电力自动化设备，2005，25（8）：32-34.

[3]杨秀媛，肖 洋，陈树勇.风电场风速和发电功率预测研究[J].中国电机工程学报，2005，25（11）：1-5.

[4]BOSSANYIEA．Short-Term Wind Prediction Using Kalman Filters[J].Wind Engineering，1985，9（1）：1-8.

[5]陈 昊.基于广义自回归条件异方差模型的负荷预测新方法[J].电力系统自动化，2007，31（15）：51-54.

[6]何 育，高 山，陈 昊.基于ARMA-ARCH模型的风电场风速预测研究[J].江苏电机工程，2009，28（3）：1-4.

[7]BAI,RUSSELL，TIAO.Kurtosis of GARCH and Stochastic Volatility Models with Nonnormal Innovations[J].Journal of Econometrics，2003（114）：349-360.

[8]BOLLERSLEV T.Generalized Autoregressive Conditional Heteroskedasticity[J].Journal of Econometrics，1986（31）：307-327.

[9]陈 昊.基于非高斯分布GARCH模型的负荷预测[J].电力自动化设备，2008，28（7）：65-68.

[10]TSAY R.Analysis of Financial Time Series[M].New York：Wiley，2002.

[11]FAN J.YAO Q.Nonlinear Time Series：Nonparametric and Parametric Methods[M].New York：Springer-Verlag，2003.