有耗色散地质介质中电磁波传播特性的FDTD计算分析

郭 江 曹俊兴 何晓燕

(成都理工大学信息工程学院,成都610059)

电磁法是重要的地球物理探测方法之一。大部分地质介质,特别是土壤,对电磁波而言是有耗色散介质。但限于问题的复杂性,在一般的电磁法数据处理解释中通常并不考虑介质色散的影响。为提高电磁探测数据的解释精度,需要将色散的影响纳入考虑。为在电磁探测数据的处理中考虑色散的影响,首先需要发展色散影响的定量计算方法,定量分析色散对电磁波场的影响。Teixeira等(1998,2000)[1,2]和 Wang等(2000)[3]先后研究发展了基于时域有限差分法(FDTD)和完全匹配层(PML)吸收边界的非均匀色散良导介质中高频电磁波场数值计算方法。自Yee于1966年提出求解麦克斯韦方程的FDTD格式[4]以来,经过半个多世纪的发展,目前已成为使用最广的电磁波场数值计算方法之一[5～7]。但用FDTD方法处理色散介质中的电磁场分布时,由于介质的介电常数是频率的函数,其本构关系在时域成为卷积关系,给直接计算带来困难,需采用递推式来计算时域卷积[1,2],这无疑将增加计算存储量和过程。本文用推广的德拜介质参数方程描述色散介质的本构关系,采用将此本构关系和场量关系直接变换为时域微分方程的方法[6],导出了有耗媒色散介质中电磁场的时域有限差分计算格式。新的计算格式适用于分析一般色散介质的电磁特性。避免了时域卷积关系的计算。采用完全匹配层(PML)吸收边界[8～11]处理边界条件,模拟分析了介质色散对电磁波传播的影响,认为一些地质介质的色散会对电磁波的传播产生不可忽视的影响。

1 色散有耗介质中场分量的FDTD差分式的推导

1.1 基本微分方程

各向同性色散介质中的Maxwell旋度方程组可以写为(仅考虑介质的介电常数为色散的情况,设介质的磁导率为常数)：

介质的本构关系为：

根据德拜关系式我们将有耗色散介质的介电常数表示为[6]

将式(4)代入式(3)可得在频域中有

考虑到对任意时变场有

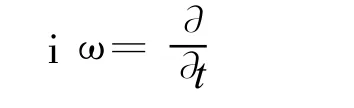
可得到(5)式在时域为

方程(1)、(2)和(6)构成了完整的电磁场时域方程组。当σ=0时,该方程组表示无电导损耗的色散介质的场方程;当时,由式(2)、(3)、(6)有

其中 ：ε=ε0ε∞。

因此,方程(1)、(7)、(8)是不计介质色散时,一般电导损耗介质的场方程。

将介质的电导损耗在介质的介电常数中考虑,会给色散介质中 FDTD公式的建立带来方便。它使我们可以将介质参数ε*(ω)和频域场分量直接变换为时域的场方程,以便进一步得到时域场分量的有限差分式,避免了由于时域卷积形式的出现所需的用迭代法求卷积值而增加的计算存储量和过程。

1.2 FDTD差分方程式

用以上导出的完整的时域场方程(1)、(2)和(6),在直角坐标系中取Yee元胞[4]为空间电磁场FDTD离散的基本单元,设 Δx=Δ y=Δ z=δ,运用中心有限差分方程式,离散(1)、(2)、(6)式,可得到9个场分量(Ex,Ey,Ez,Dx,Dy,Dz,Hx,)的差分方程式,其中x分量为：

其中：

1.3 单轴各向异性完全匹配吸收层中场量的差分格式

Gedney各向异性PM L介质中场方程仍为麦克斯韦方程的形式[10,11]

其中

为了减少截断边界引起的反射误差,ση和χη取如下渐变形式：

应注意的是,在吸收边界的不同交叠区(14)式具有不同的形式。在图1所示的区域1,完全匹配介质界面垂直x轴,此处sy=sz=1;在区域2,sx==1;在区域3=1;在区域4,=1;在区域 5,=1;在区域6,取(14)形式(即若PML介质与计算区域的分界面垂直 η轴则仅sη≠1,如 1和2区域;若PML介质与计算区域有两个分界面分别垂直 x轴或y轴,则≠1,≠1,如区域5;其他区域以此类推)。在区域1,由(12)、(14)式可得

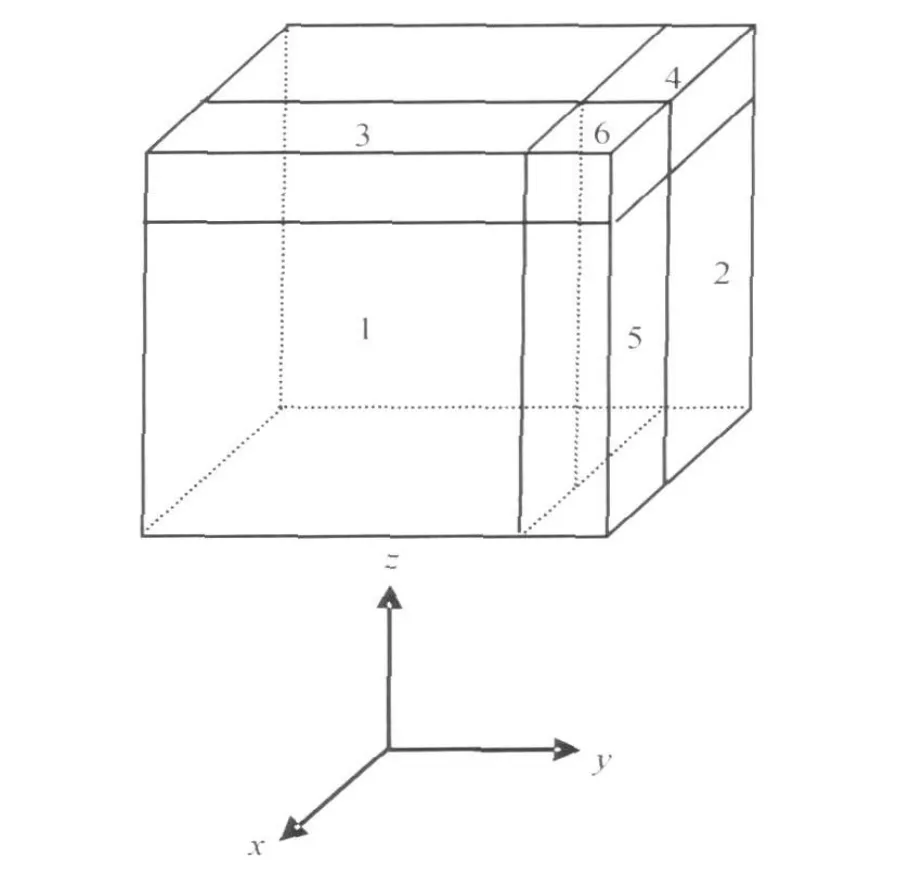
图1 各向异性完全匹配层区域示意图Fig.1 sketch of the region of the anisotropic PM L

借助辅助变量

由(15)式的第二和第三式,通过频域到时域的转换后,容易得到Dy和Dz的时域推进计算公式,其y分量为：

由(15)式第一式,通过频域到时域的转换,采用常用的FDTD离散方法可以得到的时域推进计算公式,与(10)式相同。从D′x到Ex的计算则采用以下方法,首先将式(17)转换到时域,再利用中心差分格式离散可得到的二阶精度的差分表达式

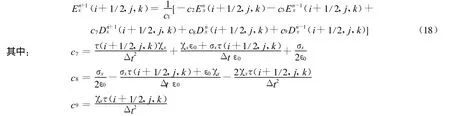
使用(16)、(11)、(18)式,可完成从H(经D)到E的时域推进计算。从E到H的推进计算可由(13)式用类似方法得到。

对交角区域6,(12)式为

为便于将(19)式过渡到时域FDTD格式,也为了避免方程中出现三阶以上的时间偏导数,引入辅助变量

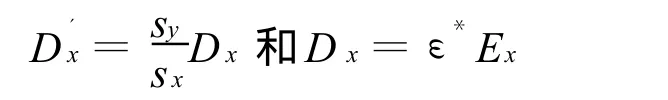
2 数值计算及分析

2.1 介质色散对电磁波场传播特性影响分析

考虑二维色散介质中Blackman-Harris脉冲源激励的电磁场的分布,设入射波上限频率为1.5×108Hz,脉冲宽度为2.5×10-8s,空间离散采用均匀网格剖分,网格尺寸取Δx=Δy=δ=0.166 m,时间步长取 Δ t=3.9×10-10s。计算空间为136×136个离散单元,场源设置在(68,68)网格处,外边界采用Gedney各向异性PML吸收边界截断。PM L的电导率表达式中

为研究介质色散对电磁波传播特性的影响,我们取计算域中距场源20δ处的点P处的电场(68,48)为分析对象。图3展示了点P处随时间的变化。分析图3所示的曲线,可知色散介质中由于色散的影响电磁波的传播位相落后于非色散介质(即在时间上有滞后),脉冲形状发生畸变,宽度有较明显的展宽,幅度减小。所以介质的色散会使电磁脉冲展宽、位相滞后、幅度减小,这在目标识别中是必须考虑的问题。

为考察色散介质电导率变化对电磁波传播的影响,我们在136×136的计算域,模拟计算了不同电导率土壤(参数=6×10-10s;电导率分别为 σ1=0,0.001 6,0.008,0.016 S/m)中电磁波的传播。场源仍用Blackman-Harris脉冲,置于计算域中心(68,68)。场域内点P(68,63)处Ez随时间的变化曲线示于图4。图4表明色散介质电导率的变化只会改变脉冲的幅度,对其传播过程中的位相、波形不会产生明显的影响。

2.2 分层介质中电磁脉冲的传播

图2 色散土壤(A)和非色散土壤(B)中不同时刻的波场(Ez)快照Fig.2 distributions at different time steps in the media with dispersion(A)and without dispersion(B)

地质雷达等电磁探测所涉及的地质介质可以用分层介质模型来近似。为研究介质色散对电磁探测的影响,我们计算了三层色散与非色散介质中的反射场。三层介质之顶层(层1)为空气;层2(模拟土壤)的电性参数为层3的电性参数为0.000 4 S/m。计算空间剖分为310×235个网格单元,层1与层2的分界面位于 z=157δ,层 2与层3的分界面位于 z=187δ,场源置于(155,155),观测点设在点P(160,156)处。计算结果如图5中的虚线所示。图5中的实线是层2作为非色散有耗介质时的反射场=0.001 6 S/m)。图5曲线上的第一个波峰是自由空间与层2界面的反射波,第二个波峰为层2与层3界面的反射波。图5表明,将土壤作为色散介质与非色散介质,反射电磁波的差别是比较大的。当将土壤(层2)作为色散介质时,空气和土壤界面的反射波幅要较作为非色散介质时的反射波幅为大,但相位相同;电磁波脉冲穿过色散介质时,其速度会降低,旅行时会增加。因此,电磁探测数据的处理应将介质的色散纳入考虑。

图3 介质色散对Ez随时间变化的影响Fig.3 Curves showing the effect of the dispersion on Ez

图4 色散介质电导率变化对Ez随时间变化的影响Fig.4 Curves showing the effect of the conductivity change on Ez

图5 观测点反射场分量Ey随时间的变化Fig.5 Curves showing the Eychange with time at the receiver

3 结论

a.用推广的德拜介质参数方程描述一般有耗色散介质的本构关系,采用将介质本构关系、场量关系直接变换为时域微分方程的方法,导出了有耗介质中电磁场的时域有限差分计算公式,避免了时域卷积关系的出现,简化了色散介质中电磁场问题的处理。

b.将Gedney单轴各向异性完全匹配边界条件应用于有耗色散介质中电磁场的模拟计算,导出了吸收层中的FDTD计算公式。数值计算结果表明,该边界条件的吸收效果良好。

c.色散介质会使电磁脉冲在传播过程中波形展宽、位相滞后、幅度减小。因此,电磁探测数据的处理解释应将介质色散的影响纳入考虑。

[1]T EIXEIRA F L,CHEW W C,STRAKA M,et al.Finite-difference time-domain simulation of ground penetrating radar on dispersive,inhomogeneous,and conductive soils[J].IEEE Trans on Geoscience and Sensing,1998,36(6)：1928-1936.

[2]TEIXEIRA F L,CHEW W C.Finite-difference computation of transient electromagnetic waves for cylin-drical geometries in complex media[J].IEEE Trans on Geoscience and Sensing,2000,38(4)：1530-1543.

[3]WANG T,ORISTAGLIO M L.3-D simulation of GRP surveys over pipes in dispersive soils[J].Geophysics,2000,65(5)：1560-1568.

[4]YEE K S.Numerical solution initial boundary problems involving Maxwell's equations in isotropic media[J].IEEE Trans on AP,1966,14(4)：302-307.

[5]TAFLOVE A.Computational Electrodynamics：The Finite-Difference Time-Domain Method[M].Boston：Artech House,1995.

[6]高本庆.时域有限差分法FDTD Method[M].北京：国防工业出版社,1995.

[7]葛德彪,闫玉波.电磁波时域有限差分方法[M].西安：西安电子科技大学出版社,2003.

[8]BERENGER J P.A perfectly matched layer for the absorption of electromagnetic waves[J].J Comput Phys,1994,114(2)：185-200.

[9]SACKS Z S,KINGSLAND D M,LEE D M,et al.A perfectly matched anisotropic absorber for use as an absorbing boundary condition[J].IEEE T rans Antennas Propagat,1995,AP-43(12)：1460-1463.

[10]GEDNEY S D.An anisotropic perfectly matched layer absorbing media for the truncation of FDTD lattices[J].IEEE Trans Antennas Propagat,1996,AP-44(12)：1630-1639.

[11]孔繁敏,李康,刘新,等.波动方程FDTD算法的PM L吸收边界条件的实现与验证[J].微波学报,2004,20(1)：1-5.

[12]王禹,袁乃昌.色散媒质中ADI-FDTD的PML[J].电子与信息学报,2005,27(10)：1677-1680.

[13]马孝义,马建仓.土壤水分介电测量的频率上限分析[J].水土保持研究,2002,9(2)：82-86.