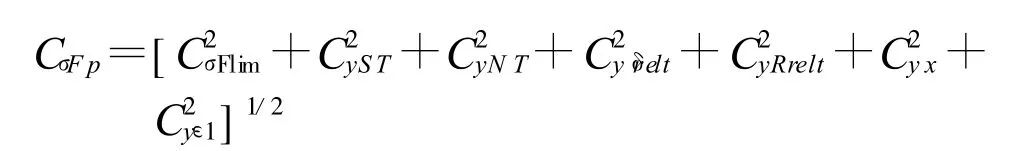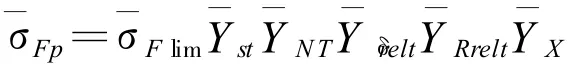调用伽玛函数实现变厚齿强度的概率可靠性调优计算

张枫念

东风汽车传动轴有限公司

1 偏置设计的变厚齿

在以往进行可靠性设计计算时,在计算得出可靠性系数后,还再要查表,才能得出可靠度值。因为直接计算时,其中的拉普拉斯函数是很麻烦的,为了手算方便,列出标准正态分布数值表供使用是很必要的,这样可减少许多计算工作量。然而这种做法在用计算机作可靠性调优计算时是很不理想的,它会阻碍计算机的自动高效的调优计算。现在可通过编程,在计算机上调用伽玛函数实现变厚齿可靠性调优计算。因为在偏置设计的变厚齿强度的计算中,可以只用变动一个参数,即变动偏移距bom就能改变强度校核的安全系数和概率可靠性设计中的可靠度。

所以用它来说明调用伽玛函数实现变厚齿强度的概率可靠性调优计算,是最为恰当的例子。偏置设计即为有一宽度为b的扇齿,此时扇齿的零变位系数截面即O-O截面在小端一侧,形成bom＞0时,则此扇齿是偏置设计,它能提高扇齿强度,见图1所示。若取bom=0,为不偏置,此时零变位截面O-O与扇齿中间截面m-m重合,称其为正置设计。任意某端截面q-q处的变位系X(q)即如下求得：X(q)=(S(q)×tgδ)/m;S(q)为距离(mm)是端截面q-q处与O-O截面的距离,它在 0～b/2范围内变动,δ为切削角,m为模数,此式可计算各不同截面的的变位系数,以及齿形参数。最后本文还对现代可靠性设计,如何建立在我们已积累了较多经验的强度校核基础上作了探讨。

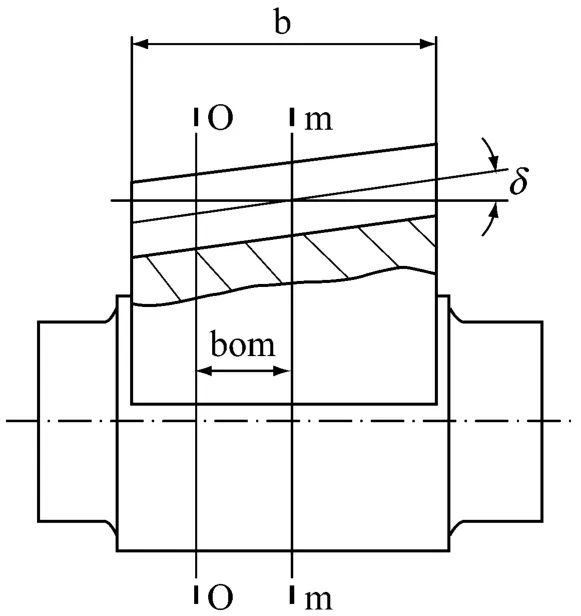
图1 偏置设计Fig.1 Offset design

2 变厚齿齿根弯曲强度校核计算

因为可靠性计算所应用的应力、强度的数学模型都是应用原来在机械零件强度校核计算中的数学模型。所以在进行变厚齿齿根弯曲强度概率可靠性计算之前,我们把变厚齿齿根弯曲强度校核计算的数学模型和校核方法作一介绍是很有必要的。

现在我们先建立直齿变厚齿的强度计算方法,由于此变厚齿是转向器摇臂轴上的变厚齿,是属于慢速大载荷的传动件,从以往实际使用中出现的失效形式得知 ,设计摇臂轴齿扇需计算扇齿的齿根弯曲强度,现提出如下方法。

(1)首先提出一个假设 ：

因为直齿变厚齿齿扇的几何特点就是各端截面的变位系数都不相同,齿廓大小也不相。因此,在这样的扇齿上沿齿宽的载荷分布是不均等的,沿齿宽的刚度大小也是不一样的。我 们假设扇齿上载荷分布的大小是与其对应的刚度成正比,而各端截面的刚度是与各截面的分度圆齿厚S成正比。变厚齿的分度圆半径r,是该齿扇的一个常量,而分度圆齿S在同一齿扇的齿宽上是变化的,大端齿厚SL最大,小端齿厚SS最小。见图1所示。

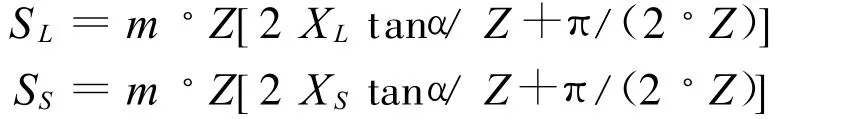
式中 ：m=齿扇模数;z齿扇全齿数

α—齿扇压力角;XL、XS—大小端变位系数。

因此扇齿的合力作用点可通过计算获得 。从图2知,如果Sx把大梯形分成两个面积相等的小梯形,即建立一方程式：为大梯形面积等于两个相同面积的小梯形。

图2 假设扇齿上载荷分布Fig.2 Gear load distribution on the assumption that

为了便于计算把上面等底角梯形改成有一底角为直角的梯形,其面积不变,把现有已知的参数代入即得：

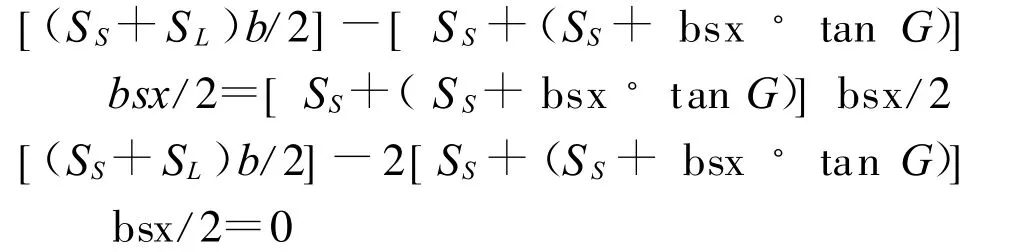
展开整理得：

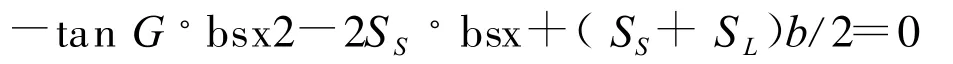
即得：

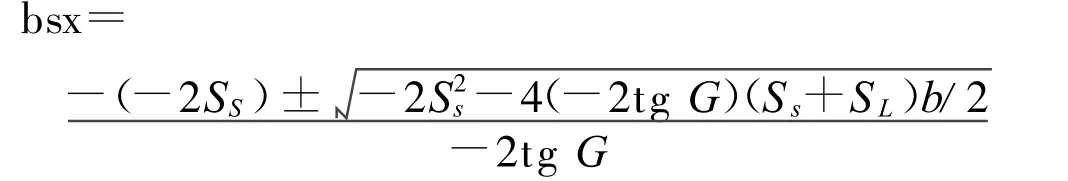
式中G=arc tan(SS+SL)/b

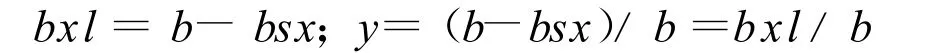
设y◦b处为合力作用点。y—合力距大端系数,y=bxl/b

现以模数m=3～6的循环球转向器为例,对常见的三种参数组合试求y值如表1所示。

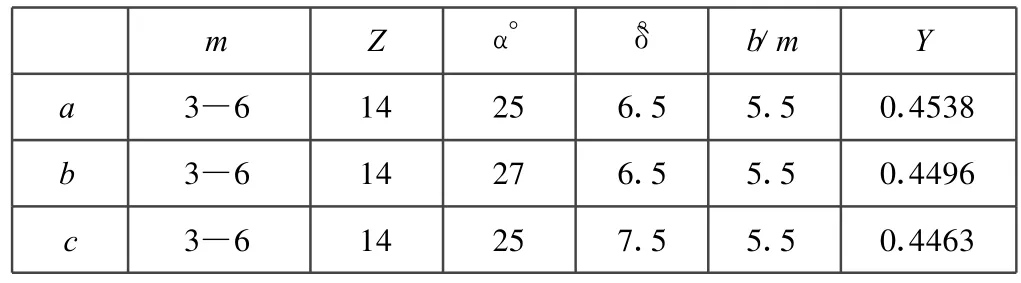
表1 常见的三种参数组合试求 y值Table 1 Common make up of three parameters demand y

表中：m模数,Z全齿数,α°压力角,δ°切削角,b/m齿宽系数合力y距大端系数。由上表知,切削角δ对y值的影响较大;当切削角δ变小,齿厚变化趋于平缓,y趋向 0.5即向齿宽中间移动,而模数m对y值的影响不大。从以上表1知y值的范围为：y=0.4538～0.4463。

因此,在简化计算时即可取 y=0.5,即将作用在齿宽中点的合力作计算载荷。并以齿宽中间端截面作为圆柱齿扇的截面,b为齿宽,以此作一圆柱齿扇 ,即构成一个变厚齿扇的当量齿扇。而这个圆柱齿扇即可按标准GB3480渐开线圆柱齿轮承载能力计算方法进行计算 。

(2)齿扇的两种载荷

1)名义载荷

在汽车转向器总成技术条件里规定,转向器疲劳试验时需在摇臂轴上施加额定输出扭矩T(即是垂臂球销上的载荷),这就是齿扇的名义扭矩载荷。

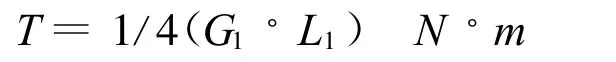
式中：L1—摇臂两孔中心距(m);G1—汽车的前轴载荷(N),名义载荷力Ft=2000T/d(N)

式中：d—分度圆直径(mm),Ft—中间端面内分度圆圆周上的名义切向力即圆周力(N)

2)计算载荷

由于转向器在工作中会产生各种附加载荷,将这些附加载荷计入,就成为计算载荷,影响附加载荷的因素很多也较复杂,这里将按GB3480阐述弯曲强度的计算切向力

式中的各项附加系数进行逐项分析选取。

KA—使用系数,考虑由于啮合外部因素,引起的动力过载影响系数,由路况不良造成较为频繁的逆向加载是KA中的主因素,按其经常行驶路况的优劣取L=1.05～1.35之间,农用车、矿用车、越野车取大些。偶尔有驶过沟槽楞坡等引起较大的逆向冲击,则纳入冲击试验范围。

KV—动载系数,是考虑齿扇啮合时振动产生内部附加载荷影响系数,因齿扇的齿面加工精度为8级,工作时的速度又较慢,即使进行疲劳试验,也不大于每分钟30次循环,因此引起的附加载荷是很小的,故取KV=1～1.05。

KFβ—齿向载荷分布系数,从大多数转向器的结构看,齿扇的中线与两支承的对称中心都不重合,大多存有一偏距S,若两支承距为L,比值S/L＞0.1即为非对称结构,此时KFβ用下式计算得

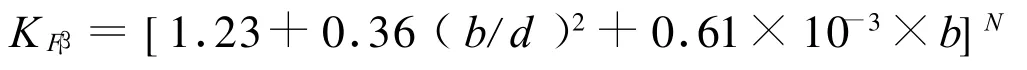
幂指数

式中：h—齿高。

KFα—齿间载荷分配系数,由于摇臂轴齿扇的重合度较低,若以齿扇中间端截面处的重合度。εam如表2所示。

一般εr=1.1～1.35取KFa=1～1.02

(3)齿根弯曲强度计算

若将扇齿看成宽为b的悬臂梁,不计摩擦力的作用,则作用于齿顶的总作用力Fbt

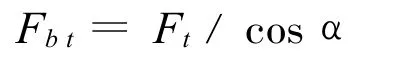
由啮合线可分解为切向力Fbt◦ cosα Fat和径向力Fbt◦Sinα Fat切向力将引起齿根弯曲应力σb径向力则引起齿根压应力σc,而压应力比弯曲应力小得多。

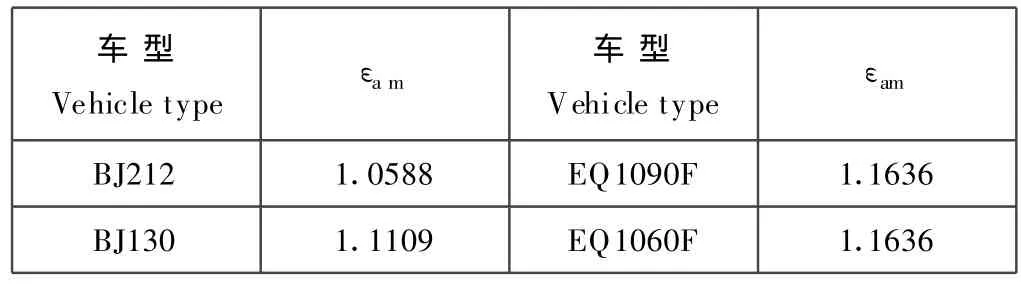
表2 重合度εa m计算值Table 2 Overlap εa mCalculating Value

确定齿根危险剖面位置的方法有多种,这里采用30°切线法,由光弹应力分析此法所确定的危险剖面位置比较符合实际。是符合α=20°的实际,而转向器扇齿α=25°～27°居多,因而与实际尚存有一定的细微误差。

1)由图3知在齿根危险剖面上所受的弯矩

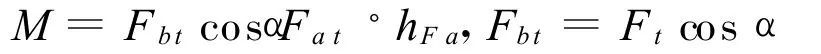
hFa—弯曲力臂,αFat—齿顶端面载荷作用角。

SFt—扇齿端面上的危险剖面齿厚。

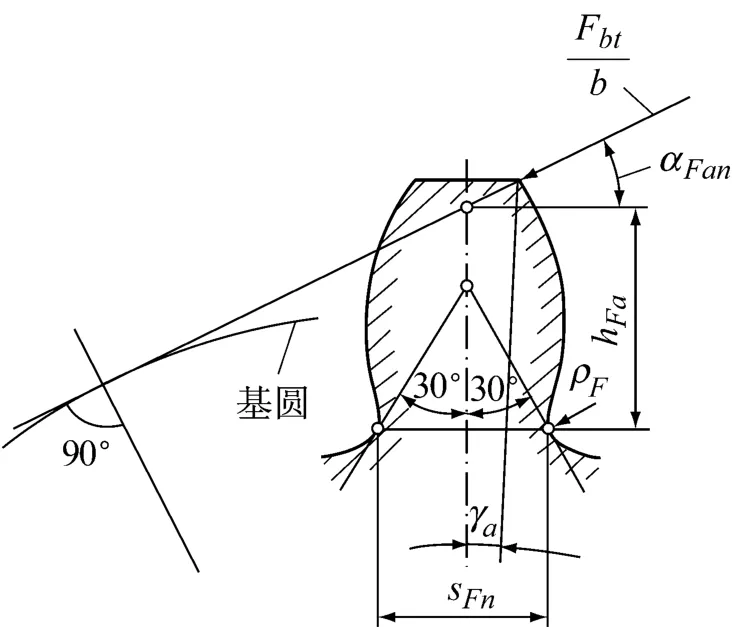
图3 30°切线法的齿根危险剖面Fig.3 30°tangent law Dedendum dangerous section

则名义齿根弯曲应力σW,从 σW=M/W 从上面知

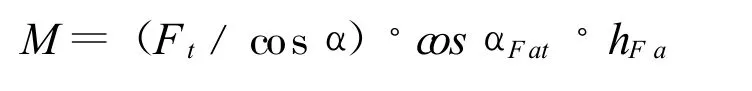
则名义弯曲应力

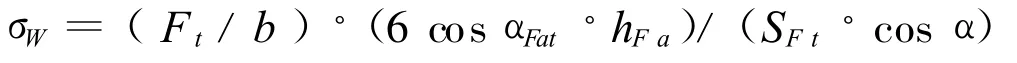
分子分母均除以m2

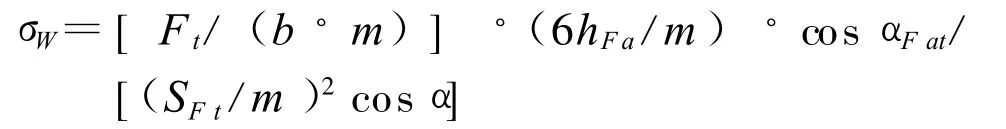
令

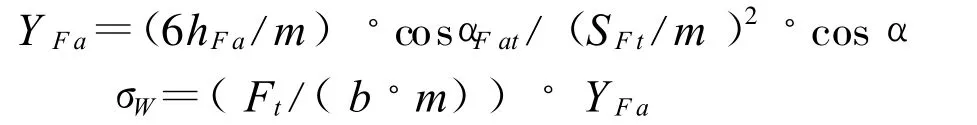
2)齿形系数YFa的具体计算。

由表2知一般转向器齿扇的重合度ε＜2,所以在计算齿根弯曲强度时计算齿形系数按GB3480要求选取YFa,按齿顶受载的那一种,即按表3计算

YFa是考虑当载荷作用于齿顶时,齿形对名义弯曲应力的影响。计算YFa,主要是要算出SFn、hFa及齿形系数YFa,可按表3算得,先设定刀具是采用无凸台的齿条形刀具如图4所示 。E—为刀齿对称线的距离hf p—为齿条形刀具于刀齿厚Sc=(πm/2)处的刀齿齿顶高,即刀具的分度截面处的齿顶高,α—齿条刀具齿形压力角 ,ρ f p—齿条形刀具齿顶两圆角半径。计算时的变位系数X取齿扇中间端截面的变位 系数x=Xm齿顶压力角αa同样也取中间端截面的齿顶压力角为αa=αam,αam=arc cos(d b/dam),

图4 刀具轮廓尺寸Fig.4 Contour Tool Size

dam—齿扇中间端截面处的齿顶圆直径,db—基圆直径。齿顶受载齿形系数YFa的有关计算公式

刀尖圆心至刀齿对称线的距离E

辅助角值θ=(2G/Z)tgθ-H,用牛顿迭代法解,

初值θ=-H/(1-2G/Z)

危险剖面齿厚SFn

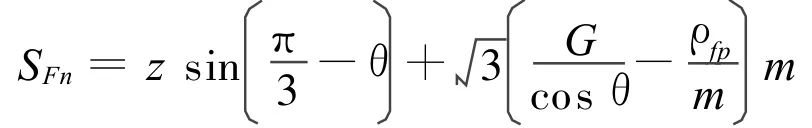
30度切点处曲率半经/m ：

齿顶压力角αav=Arc cos(rb/ra)

齿顶圆齿厚半角 γ α

弯曲力臂/m ：

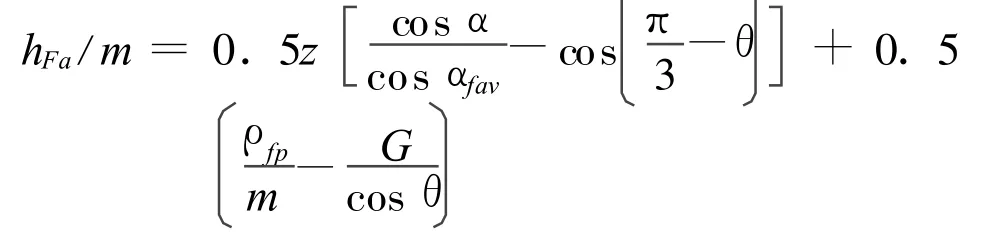
齿形系数齿形系数yFa=[6(hfa/m)Cos(αFav)]/[(sf/m)2Cos(α1)]

3)应力修正系数Ysa,载荷作用齿顶是的修正系数,应力修正系数Ysa。是将名义弯曲应力换算成齿根局部应力的系数 。它考虑了齿得过渡曲线处的应力集中效应 ,以及弯曲应力以外的其它应力的影响 。齿根的局部应力σFa

式中 ：La=SFa/hFa;qs=SFa/2ρ f

再用弯曲强度计算的重合度系数yε对上述局部应力进行修正成为齿根基本应为σF0

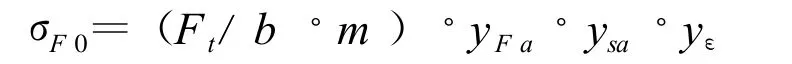
yε一是将载荷由齿顶转换到单对齿啮合区上界点的系数,对转向器齿扇 、齿条啮合的重合度都在1＜εam＜2的范围内 ,则 yε可由下式算得,yε=0.25+0.75/εam(因为以上选齿顶受载齿形系数YFa中不包含重合度系数;但计算齿根应力基本值σF0时应包括)

再考虑到载荷各系数的影响,齿根的计算应力为

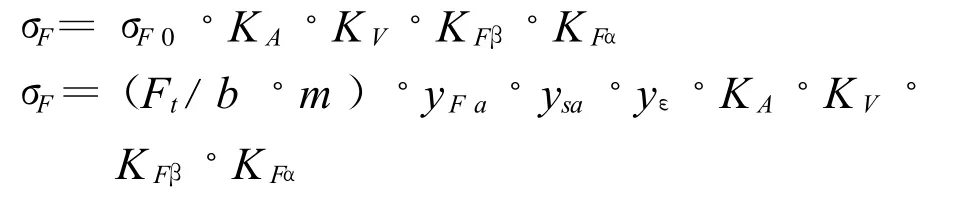
(4)许用齿根应力σFp的计算

1)弯曲疲劳极限σFlim

根据齿扇所使用的材料,直接从GB3480中查取。σFlim值。材质及热处理均为优良者取上限,否则相应递减。摇臂抽齿扇多为合金钢进行渗碳淬火,其硬化层深度δ≥0.15m(m为扇齿模数),硬度HRC58—62时,一般 σFlim=350-520 N/mm2。因为目前实际生产技术水平存有一定的离散性,下面的算例取σFlim=485～510

2)计算齿扇的许用齿根应力σFp

由于所计算齿扇与标准中直接选取的σFlim值,存在试验条件不同等因素,必须进行相应的修正,因此齿扇的许用齿根应力为：σFP=(σFlim◦yST◦yNT/SFmin)◦yδrelT◦yRrelT◦yX;式中：yST—选用 σFlim值的修正系数,当按GB3480标准选用 σFlim值时,规定yST=2.0

yNT—弯曲强度的寿命系数,用来考虑当齿轮只要求有限寿命 N＜3×106时,齿扇的许用齿根应力可以提高的系数。现行的汽车转向器总成质量分等标准QC/T29.098,规定转向器疲劳试验的循环次数,优等品为2.5×106,一等品为2×106,合格品为1.5×106在计算时应立足于高起点取NL=2.5×106次循环yNT=(3×106/NL)0.115

yδrelT—持久寿命时的相对齿根圆角敏感系数,是考虑所计算的材料、几何尺寸等对齿根应力的敏感度与疲劳极限σFlim的求得有所不同,而引入的系数。系数yδrelT可按下式算得

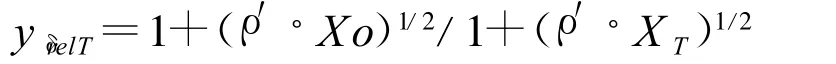
式中 ρ′—材料滑移层厚度,渗碳淬火钢 ρ′=0.003 mm

Xo—齿很危险剖面处的应力梯度与最大应力的比值。

Xo=1/5(1+qs),qs—齿根圆角参数,qs=SFt/ρ f

XT试验疲劳极限时齿根危险剖面处的应力梯度与最大应力的比值,XT≈1/5(1+qsT)GB3480推荐qsT=2.5

yRrelT—持久寿命时相对齿根表面状况系数,是考虑齿廓根部的表面状况,主要是齿根圆角处的粗糙度对齿根弯曲度的影响,摇臂轴齿扇齿面粗糙度Rz=10-20之间,故可采用下式计算

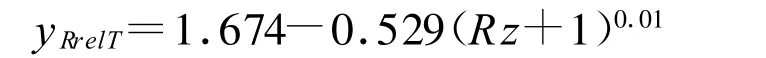
yx—弯曲强度计算的尺寸系数yx,是考虑在尺寸增大(扇齿模数m＞5 mm)时,使材料强度降低的尺寸效应系数,主要影响因素是材料及其硬度和结构尺寸。由GB3480弯曲强度计算的尺寸系数yx图可知在扇齿模数m≤10时,yx=1

本例扇齿模数5 mm＜m＜8 mm,弯曲强度计算的尺寸系数yx=1

(5)弯曲强度的计算安全系数SF

本例齿根弯曲强度的校核计算到此就结束。

3 变厚齿齿根弯曲强度的概率可靠性计算

由以上所述知变厚齿齿根弯曲强度校核计算的计算量很大,世界各国也都有其相应的标准,如我国就有GB3480渐开线圆柱齿轮承载能力计算方法。由于是采用分离系数法可以把计算分成很多细项来研究,多少年来里面积累了无数前人的经验和研究成果,使计算方法变得比较完善、成熟。但计算量也越来越大。自从有了计算机辅助计算,大大减轻了强度校核的负担。如果对分离系数的诸多细项建立了相关的随机变量处理的机制和方法,并积累了足够的随机数据资料,便可以开展概率可靠性计算。

(1)变厚齿齿根弯曲正应力概率模型

对于已知载荷作用于齿顶时齿根弯曲正应力σF的计算公式如下：

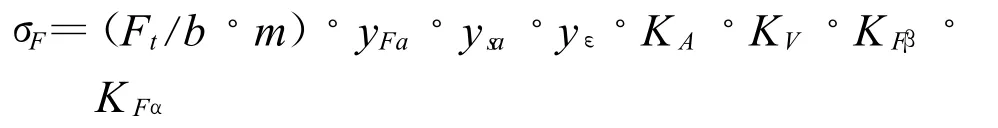
齿根弯曲正应力σF的分布规律尚无统一定论,这里定为服从对数正态分布,为齿根弯曲正应力σF概率模型 。其 σF的均值

计算弯曲应力σF的变异系数

齿间载荷分布系数变异系数Ckfα=0.033KFα;作用力变异系数Cft=0.049;使用系数变异系数Cka=0.046;速度系数变异系数Ckv=0.04;齿向载荷分布系数变异系数Ckfβ=0.033;齿间载荷分布系数变异系数 Ckfα=0.033.

(2)变厚齿齿根抗弯曲疲劳强度概率模型齿扇的齿根抗弯曲疲劳强度σFp的计算公式如下：

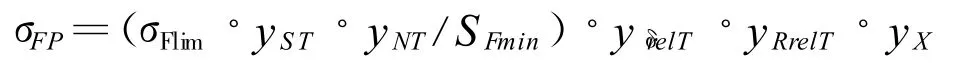
这里设定为服从对数正态分布,为齿根抗弯曲疲劳强度σFp的概率模型,其σFp的均值

与变异系数CσFp分别为：渗碳淬火钢弯曲疲劳极限σFlim的变异系数CσFlim=0.0813;弯曲疲劳极限应力修正系数yST的变异系数CyST=0.047619;寿命系数yNT的变异系数CyNT=0.03;圆角敏感系数yδrelt的变 异 系数 Cyδrelt=0.033;齿 根表 面 状况 系 数yRrelt的变异系数CyRrelt=0.05;尺寸系数 yx的变异系数Cyx=0.02;重合度系数变异系数Cyε1=0.0278