A NEW WAKE OSCILLATOR MODEL FOR PREDICTING VORTEX INDUCED VIBRATION OF A CIRCULAR CYLINDER*
XU Wan-hai
Key Laboratory of Port and Ocean Engineering, Tianjin University, Tianjin 300072, China,
E-mail: wanhaixu@hotmail.com
WU Ying-xiang, ZENG Xiao-hui, ZHONG Xing-fu
Key Laboratory for Hydrodynamics and Ocean Engineering, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
YU Jian-xing
Key Laboratory of Port and Ocean Engineering, Tianjin University, Tianjin 300072, China
A NEW WAKE OSCILLATOR MODEL FOR PREDICTING VORTEX INDUCED VIBRATION OF A CIRCULAR CYLINDER*
XU Wan-hai
Key Laboratory of Port and Ocean Engineering, Tianjin University, Tianjin 300072, China,
E-mail: wanhaixu@hotmail.com
WU Ying-xiang, ZENG Xiao-hui, ZHONG Xing-fu
Key Laboratory for Hydrodynamics and Ocean Engineering, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
YU Jian-xing
Key Laboratory of Port and Ocean Engineering, Tianjin University, Tianjin 300072, China
This article proposes a new wake oscillator model for vortex induced vibrations of an elastically supported rigid circular cylinder in a uniform current. The near wake dynamics related with the fluctuating nature of vortex shedding is modeled based on the classical van der Pol equation, combined with the equation for the oscillatory motion of the body. An appropriate approach is developed to estimate the empirical parameters in the wake oscillator model. The present predicted results are compared to the experimental data and previous wake oscillator model results. Good agreement with experimental results is found.
vortex induced vibration, wake oscillator model, circular cylinder, van der Pol equation
1. Introduction
Vortex-Induced Vibration (VIV) is caused by the vortex shedding behind bluff bodies and may lead to degradation of structural performance or possibly even structural failure. It is a particularly important issue for offshore structures such as pipes, risers and mooring lines, therefore, it must be considered in engineering designs. Recent reviews on the VIVs can be found in Ref.[1-3].
Several ways were adopted to predict the dynamic behavior of structures experiencing vortex induced vibration in the literature. One VIV prediction method consists of solving the Navier-Stokes equations by the Direct Numerical Simulation (DNS) for the fluid around the circular cylinder and to compute the hydrodynamic loads on it[4,5], however, this approach is made difficult by the fact that Reynolds numbers in most industrial applications cannot be well estimated. A well-known alternative is to use phenomenological models based on wake oscillators. Combined with accessible analytical considerations, they help reveal the underlying physical nature. This explains several recent improvements in this approach. The original kernel in the form of van der Pol or Rayleigh equation was reinterpreted by Skop and Balasubramanian[6], Skopand Luo[7], Krenk and Nielsen[8]and Plaschko[9]. More recently, Facchinetti et al.[10]presented an excellent review on the dynamics of wake oscillator models for 2-D vortex-induced vibrations. Three different types of coupling effects (displacement, velocity and acceleration) of the cylinder movement on the lift fluctuation were considered. It is found that by the displacement and velocity couplings only, one fails to predict the lift phase observed in experiments of vortex shedding from cylinders that were forced to oscillate. By the displacement coupling alone, the lift magnification at lock-in and almost all important features of vortex induced vibrations at low values of the Skop Griffin parameterSGcan not be predicted, while by the velocity coupling alone, the range of lock-in for low values ofSGcan not be determined. On the other hand, the acceleration coupling may be used to qualitatively model the features of VIV considered. The same authors[11]extended the model to predict VIV and Vortex Induced Waves (VIW) for cables and successfully predicted the experimental response behavior of a towed cable. Mathelin and De Langre[12]extended Facchinetti’s results to predict VIV of cables subjected to sheared flows. Violette et al.[13]predicted the vortex-induced vibrations of long structures using a wake oscillator model developed by Facchinetti et al.[10], and compared the predicted results with DNS and experimental results. Lin et al.[14]modified the fluid damping used in the structure-wake oscillators proposed by Facchinetti et al.[10], into a nonlinear fluid damping in the form of the square-velocity in the response analysis of vortex induced vibrations.
The wake oscillator model presented by Facchinetti et al.[10]can qualitatively reproduce some aspects of VIV for rigid cylinders elastically supported, but fails to describe quantitatively the cylinder oscillation amplitude, also no relations were obtained between the model parameters in the model, which would vary considerably from experiment to experiment. This study aims to overcome these shortcomings, by modifying Facchinetti’s model and applying a new approach to estimate the empirical parameters in the wake oscillator model.
This article is divided in five sections. Brief descriptions of the structural and wake oscillator model are given in the next section. In section 3, the empirical parameters are estimated from experimental data based on a forced wake oscillator for the vortex shedding behind a structure whose movement is imposed. Then, the comparations of the present model results are made with the experimental data and Facchinetti’s model results in Section 4. Finally, in the last section, conclusions are drawn based on the obtained results.

Fig.1 Model of coupled structure and wake oscillators for 2-D vortex-induced vibrations
2. Model description
Consider the elastically supported rigid circular cylinder shown schematically in Fig.1. The coupling wake and structure oscillators are described by[10]:

where the dot represents the derivative with respect to dimensionlesst,yis the dimensionless in-plane cross-flow displacement of the structure, and the dimensionless wake variableq(Fig.1) may be associated to the fluctuating lift coefficient on the structure,Aandεare the empirical parameters,ξandδare the structure reduced damping and angular frequency, respectively,γis a stall parameter[6,7],μis mass ratio,Mis essentially a mass parameter for the effect of the wake on the structure. The above parameters are related by the following expressions:

whereCL0is the reference lift coefficient of a fixed structure subjected to vortex,Dis the diameter of the circular cylinder,Uis the free stream velocity of the uniform flow,Stis the Strouhal number,ΩsandfΩare the vortex shedding angular frequency and the structure angular frequency, respectively,Uris the reduced velocity,CDis the drag coefficient of the structure,mis the structural mass, including the fluid-added mass, andρis the fluid density.
3. The determination of empirical parameters
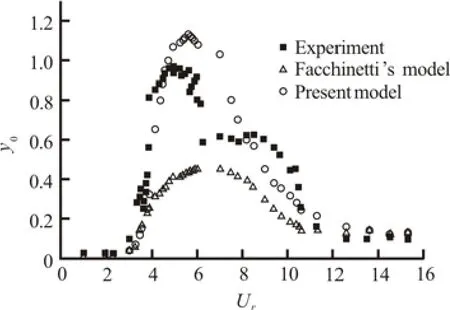
All parameters presented above are estimated in this section, assumingSt=0.2,CL0=0.3 in the sub-critical range, 300 Fig.2 Lock-in bands in the (ω,y0) plane for synchronization of vortex shedding with transverse cylinder vibration. Experimental data Considering an harmonic motion with dimensionless amplitudey0and angular frequencyω, namelyy=y0cos(ωt), the actionfof the structure on the fluid wake oscillator can be expressed as: A reduced velocity is defined based on the forcing frequency asUr=1/(ωSt)[10]. With the hypothesis of harmonicity and frequency synchronization, the response is sought in the formq=q0cos(ωt−ψ), whereq0andψare timeindependent amplitude and phase, respectively. Substituting them into the wake oscillator, Eq.(1), and considering only the main harmonic contribution of the nonlinearities, with some elementary algebraic operations, one obtains the amplitude of the transfer function o f the wake oscillator, with the same form as shown inRef.[10]: The free wake oscillator responseq0=2 is supposed to prevail on the forced response, which defines a lock-out state, as a boundary defined by polynomial (4) in the (ω,y0) plane. The lock-in domain is shown in Fig.2, the parameterAmay now be chosen by matching the model response (4) to experimental data on the lock-in extension in the literature, which can be expressed as: For a given set of model parameters, the amplitude of the cylinder vibration is a function of the structural damping factor, the mass ratio, as well as the ratio of the nominal vortex shedding frequency to the natural frequency of the cylinder structure. However, the maximum structure displacement amplitude at the lock-in is typically expressed in the literature as a function of a single combined mass-damping parameter, namely the Skop-Griffin parameterS(=2π3St2μξ). Recently, Sarpkaya[1] Gdevised a new and relatively simple curve-fitting given by for a rigid cylinder, as is plotted in Fig.3. Facchinetti et al.[10]defined a reference resonance state by lettingω=δ=1 atUr=1/St, the maximum structure displacement amplitude is obtained and can be written as: The direct substitution of Eqs.(5) and (6) into Eq.(7) gives the empirical parameterε. In fact,εdepends on the material properties of the structure, instead of being a universal constant. Fig.3 Experimental measurements of the modally normalized maximum amplitude versus the Skop-Griffin parameterSGand the proposed curve-fitting: Eq.(6) (Sarpkaya[1]) In this section, firstly, comparisons of the calculations based on the present wake oscillator model, experiments by Khalak and Williamson[15]and the precious wake oscillator model by Facchinetti et al.[10]are made. The circular cylinder is subjected to an incident uniform flow, and supported by a spring and a damper. The same mass and damper coefficients used in Khalak and Williamson[15]were used in the present numerical investigation. They are:ξ=5.42× 10−3andμ=2.4 with the reduced velocity varying from 1 to 16 Figure 4 shows the amplitude of the oscillation as a function of the reduced velocity obtained in the present work and other numerical, experimental data. It can be seen that the present model can be used to capture the initial, upper and lower branches reported in Khalak and Williamson[15]. The numerical results obtained for the upper branch are quite close to the experimental data. However, those obtained by Facchinetti’s model[10]obviously deviate from the experimental data. The vibration frequency is plotted in Fig.5. The new wake oscillator model results seem to agree fairly well with the experimental data at low values of the reduced velocity, but underestimate the vibration frequency at high values of the reduced velocity. Fig.4 The oscillation amplitude of the elastically supported rigid circular cylinder as a function of reduced velocity Fig.5 The oscillation frequency of the elastically supported rigid circular cylinder as a function of reduced velocity A striking phenomenon was found by Govardhan and Williamson[16]who studied the transverse VIV of a cylinder of low mass and low damping with no structural restoring force. The mass ratioμwas 0.52, which is less than the“critical mass ratio” (0.542 as obtained by a group of free excited vibration tests), with the reduced dampingξ=0.0052. Present wake oscillator model and the previous model by Facchinetti et al.[10]are both able to describe the phenomenon of the persistent lock-in, as is illustrated in Fig.6, where the structural oscillation amplitudey0is plotted as a function of the reduced velocityUr. It appears that, our model results agree better with experimental data, while the predicted results by Facchinetti’s model are lower than experimental results. The evolution of frequency is plotted in Fig.7, where the results of the present wake oscillator model and Facchinetti’s model results are both consistent with experimental data. Fig.7 The oscillation frequency of the elastically supported rigid circular cylinder as a function of reduced velocity. ξ=5.2× 10−3and μ=0.52 From the case studies described above, it can be seen that the new wake oscillator model can predict the rigid cylinder VIV qualitatively and quantitatively. A new wake oscillator model is presented for the vortex induced vibration of an elastically supported cylinder. It is different from the wake oscillator model proposed Facchinetti et al.[10], with a set of relations postulated between the empirical parameters and the mass ratio and damping parameters that govern the oscillatory response. These relations are used to calculate empirical parameters which were assumed constants by Facchinetti et al.. The model was successfully used to predict quantitatively the resonant response amplitude and frequency for elastically supported cylinder. The predicted results are compared to the experimental data and Facchinetti’s model results, with a good agreement with experimental data. The model has overcome some shortcomings in Facchinetti’s model. These results show the applicability and usefulness of the present model for predicting vortex induced vibration of engineering structures. Finally, as a challenging task, it is desirable to extend the present model to elastic structural elements such as risers, cables, etc.. [1] SARPKAYA T. A critical review of the intrinsic nature of vortex-induced vibrations[J].Journal of Fluids and Structures,2004, 19(4): 389-447. [2] GABBAI R. D., BENAROYA H. An overview of modeling and experiments of vortex -induced vibration of circular cylinders[J].Journal of Sound and Vibration,2005, 282: 575-616. [3] Williamson C. H. K., GOVARDHAN R. A brief review of recent results in vortex-induced vibrations[J].Journal of Wind engineering and industrial Aerodynamics,2008, 96(6-7): 713-735. [4] NEWMAND J., KARNIADAKISG E. A direct numerical simulation study of flow past a freely vibrating cable[J].Journal of Fluid Mechanics,l997, 344: 95-136. [5] SHA Yong, WANG Yong-xue. Vortex induced vibrations of finned cylinders[J].Journal of Hydrodynamics,2008, 20(2): 195-201. [6] SKOP R. A., BALASUBRAMANIAN S. A new twist on an old model for vortex-excited vibrations[J].Journal of Fluids and Structures,1997, 11(4): 395-412. [7] SKOP R. A., LUO G. An inverse-direct method for predicting the vortex-induced vibrations of cylinders in uniform and nonuniform flows[J].Journal of Fluids and Structures,2001,15(6): 867-884. [8] KRENK S., NIELSEN S. R. K. Energy balanced double oscillator model for vortex-induced vibrations[J].ASCE Journal of Engineering Mechanics,1999, 125(3): 263-271. [9] PLASCHKO P. Global chaos in flow-induced oscillations of cylinders[J].Journal of Fluids and Structures,2000, 14(6): 883-893. [10] FACCHINETTI M. L., DE LANGRE E. and BIOLLEY F. Coupling of structure and wake oscillators in vortex-induced vibrations[J].Journal of Fluids and Structures,2004,19(2): 123-140. [11] FACCHINETTI M. L, DE LANGRE E. and BIOLLEY F. Vortex-induced travelling waves along a cable[J].European Journal of Mechanics B/Fluids,2004, 23(1): 199-208. [12] MATHELIN L., DE LANGRE E. Vortex-induced vibrations and waves under shear flow with a wake oscillator model[J].European Journal of Mechanics B/Fluids,2005, 24(4): 478-490. [13] VIOLETTE R., DE LANGRE E. and SZYDLOWSKI J.Computation of vortex-induced vibrations of long structures using a wake oscillator model: Comparison with DNS and experiments[J].Computers and Structures,2007, 85(11-14): 1134-1141. [14] LIN Li-ming, LING Guo-can and WU Ying-xiang et al. Nonlinear fluid damping in structure-wake oscillators in modeling vortex-induced vibrations[J].Journal of Hydrodynamics,2009, 21(1): 1-11. [15] KHALAK A., WILLIAMSON C. H. K. Investigation of relative effects of mass and damping in vortex-induced vibration of a circular cylinder[J].Journal of Wind Engineering and Industrial Aerodynamics,1997, 69-71: 341-350. [16] GOVARDHAN R., WILLIAMSON C. H. K. Modes of vortex formation and frequency response of a freely vibrating cylinder[J].Journal of Fluid Mechanics,2000, 420: 85-130. October 30, 2009, Revised January 5, 2010) * Project supported by the National High Technology Research and Development Program of China (863 Program, Grant No. 2006AA09Z350), the National Natural Science Foundation of China (Grant No.10702073) and the Knowledge Innovation Program of Chinese Academy of Sciences (Grant No. KJCX2-YW-L02). Biography:XU Wan-hai (1981-), Male, Ph. D. 2010,22(3):381-386 10.1016/S1001-6058(09)60068-8
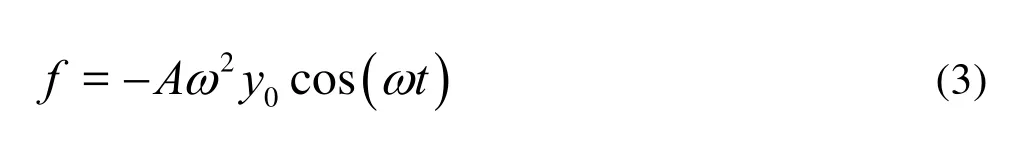
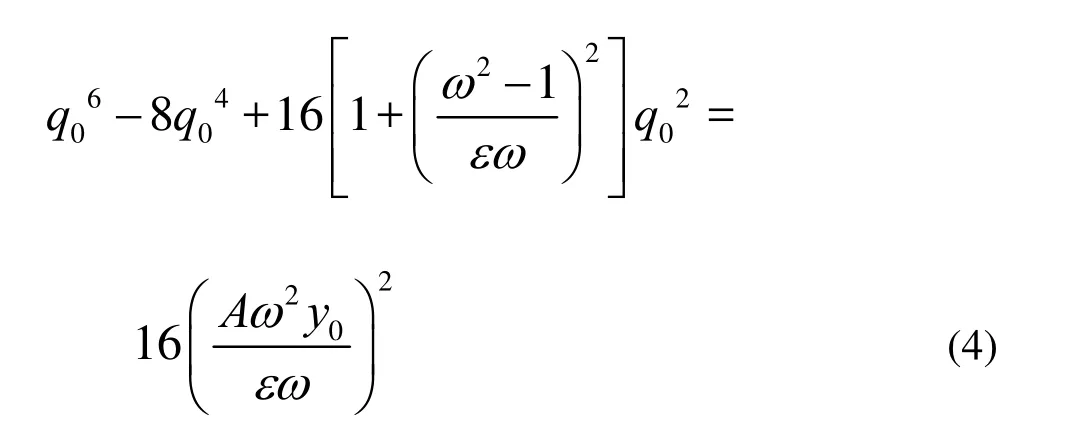




4. Numerical results and discussion


5. Conclusions
- 水动力学研究与进展 B辑的其它文章
- BROADBAND ROTOR NOISE PREDICTION BASED ON A NEW FREQUENCY-DOMAIN FOUMULATION*
- THE EFFECT OF RECLAMATION IN AREAS BETWEEN ISLANDS IN A COMPLEX TIDAL ESTUARY ON THE HYDRODYNAMIC SEDIMENT ENVIRONMENT*
- IMPROVED DEM-CFD MODEL AND VALIDATION: A CONICAL-BASE SPOUTED BED SIMULATION STUDY*
- FLOWS THROUGH ENERGY DISSIPATERS WITH SUDDEN REDUCTION AND SUDDEN ENLARGEMENT FORMS*
- NUMERICAL SIMULATIONS OF WAVE-INDUCED SHIP MOTIONS IN TIME DOMAIN BY A RANKINE PANEL METHOD*
- SENSITIVITY STUDY OF THE EFFECTS OF WAVE-INDUCED VERTICAL MIXING ON VERTICAL EXCHANGE PROCESSES*

