NUMERICAL SIMULATIONS OF WAVE-INDUCED SHIP MOTIONS IN TIME DOMAIN BY A RANKINE PANEL METHOD*

CHEN Jing-pu

China Ship Scientific Research Center, Shanghai 214082, China, E-mail: Chjp702@163.com

ZHU De-xiang

Shanghai Institute of Computing Technology, Shanghai 200040, China

NUMERICAL SIMULATIONS OF WAVE-INDUCED SHIP MOTIONS IN TIME DOMAIN BY A RANKINE PANEL METHOD*

CHEN Jing-pu

China Ship Scientific Research Center, Shanghai 214082, China, E-mail: Chjp702@163.com

ZHU De-xiang

Shanghai Institute of Computing Technology, Shanghai 200040, China

A time domain prediction of wave-induced ship motions by a Rankine panel method is investigated. Linear boundary conditions on free surface and mean wetted body surface are adopted, while the numerical damping method is used for the radiation conditions. The motions of two ships in regular head waves are computed by the present method. The related numerical results are compared with the experiment data and those from linear strip theory. The comparison shows satisfactory agreements for pitch and heave transfer functions.

Rankine source, panel method, time domain, ship motion, forward speed

1. Introduction

The numerical methods for prediction of wave-induced ship motions and wave loads are numerous: 2-D strip methods, 3-D frequency domain and time domain methods of potential flow theory, etc.[1]. At present, Numerical Wave Tank (NWT) based on CFD draw researchers’ attentions, many approaches, and a variety of techniques, such as CIP, VOF, level-set and MAC[2-5]are under studying for solving the problems on fully nonlinear free surface and large amplitude ship motions. The 3-D frequency-domain methods are widely adopted in offshore engineering. The 3-D time-domain methods are of great superiority in solving ship motions with forward speed, the large amplitude body motions and nonlinear free surface can be incorporated in these methods. The NWTs based on viscous flow can predict fully nonlinear free surface waves and large amplitude body motions, however, the complexity ofthe numerical model and long time-consuming limit the wide application of these kinds of methods, so the applications of NWTs for global ship motions are not mature now.

Within the framework of potential flow theory, the 3-D panel methods in time-domain are practical for solving ship motions with forward speed. According to the Green functions, the panel methods include two categories: the time-domain Green function and the Rankine source. The methods based on time-domain Green function satisfy the Neumann-Kelvin type free surface conditions and different level of body nonlinearities can be taken into account[6-8]. However, the time-domain Green function is limited to linear free surface conditions. The Rankine source does not satisfy any boundary conditions, such as, free surface and body conditions. Therefore, the Rankine source is very flexible for numerical simulations of hydrodynamics and Rankine panel methods are very successful tools for solving nonlinear wave making problems[9-11]. The Rankine panel methods have been extended to wave-induced ship motions in time domain. In 1993, Ferrant[12]presented a method for wave-induced ship motions based on the Rankine source. In order to take into account more nonlinear effects, Kring[13]and Huang[14]put forward the weak-scattering theory with a Rankine panel method, which includes the nonlinear restoring force and Froude-Krylov force. The Large Amplitude Motion Program (LAMP) also employs the Rankine panel method and mixed source formulations are used for radiation conditions[15]. Recently, Kim and Kim[16]developed a time-domain Rankine method named WISH under the support of five shipyards of Korean and Korean Register.

In this article, we carry out the investigation on numerical simulations for wave-induced ship motions in time domain by a Rankine panel method. The linear condition on free surface and mean wetted body surface are employed for this study. In order to satisfy the radiation condition, the numerical damping beach is used. Finally, the numerical results of simulated cases for two ships with forward speed are presented and discussed.

2. Basic formulation

2.1Coordinate systems

In this article, three coordinate systems are used: the earth-fixed systemOxyz, the body-fixed systemO0x0y0z0and the auxiliary systemO′x′y′z′. The earth-fixed systemOxyzis an inertial system, fixed in space. The Body-fixed systemO0x0y0z0is fixed on the ship, which rotates and translates with the ship.O0is located at the center of ship mass, whileO0x0points to the bow,O0y0to the starboard andO0z0is pointing up . The auxiliary systemO′x′y′z′ moves with the speed of ship, and thex′y′-plane locates at the mean free surface. The detailed relations of the three coordinate systems can be found in Ref.[6].

2.2Governing equations

In order to predict the wave-induced ship motions, the fluid is assumed to be inviscid, incompressible and the flow is irrotational. Therefore, a total velocity potentialΦTis introduced to describe the flow field. Under the linear assumption, the total velocity potentialΦTcan be expressed as the sum of incident wave velocity potentialΦIand disturbed velocity potentialΦ:

The Laplace equation is used as the governing equation:

whereΩdenotes the flow domain.

The linear free surface conditions are adopted on the undisturbed free surface atz=0, including linear kinematic condition:

and linear dynamics condition: whereζis the disturbed free suface elevation.

The body boundary condition satisfies on the mean wetted body surface :Sb

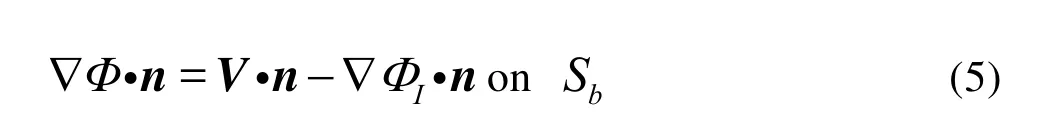
wherenis the body surface normal onSb, pointing away from the fluid,Vis the body surface velocity.

The fluid disturbance must vanish at infinity, and there exists the radiation condition on free surface:

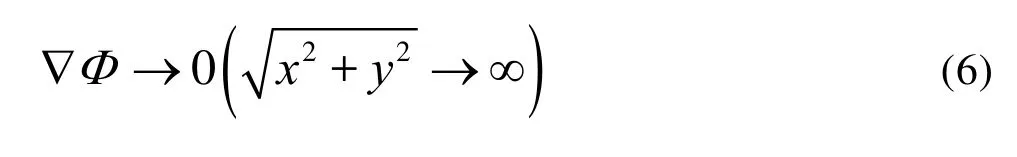
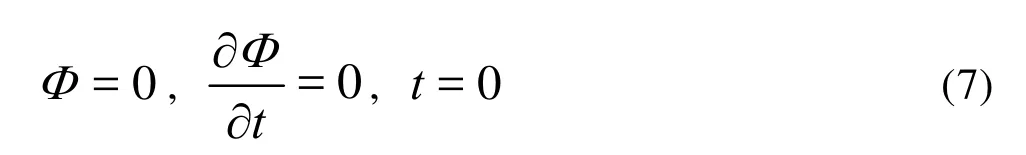
while the initial conditions are as follows: is set up, the disturbed potentialΦcan be figured potentialΦIis already known. According to the linear Bernoulli equation, the pressure on body surface due to disturbed potential and incident-wave potential is computed as follows:

2.3Equation of motions

The initial boundary value problem of Eqs.(2)-(7) out by using numerical method. The incident wave

whereρis the density of water,pHDthehydrodynamic pressure due to disturbed potentialΦ,pFKthe incident-wave pressure, hydrostatic pressure is computed by

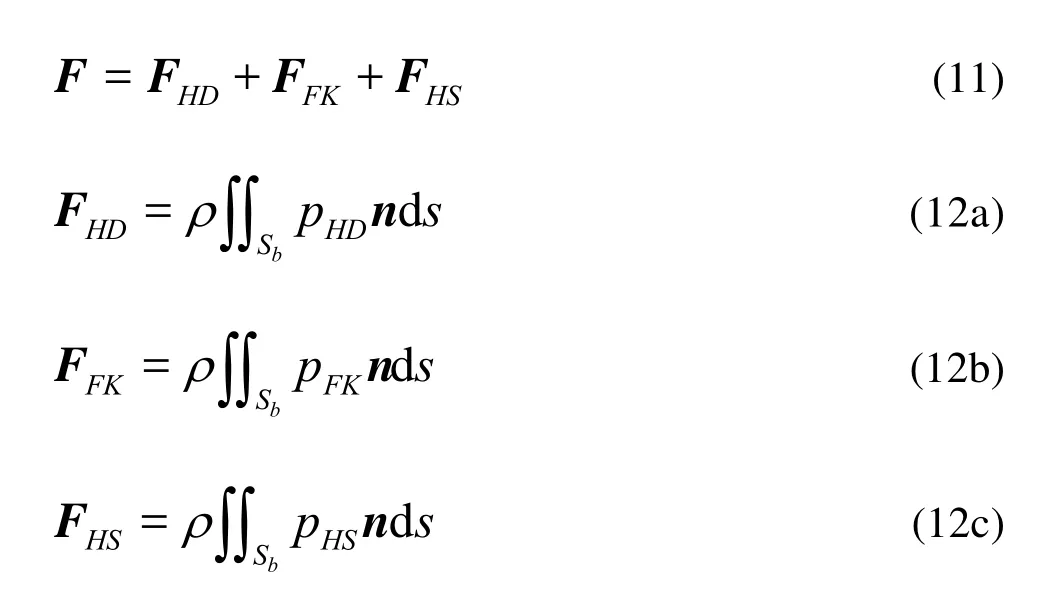
The forcesFacting on the body surface can be calculated by integrating the corresponding pressure on the mean wetted surfaceSb: whereFHDis the hydrodynamics force due to disturbed potentialΦ,FFKis the Froude-Krylov force,FHSis the hydrostatics (n1,n2,n3)=nand (n4,n5,n6)=r×n.

After the forces and moments on the ship have been determined from the above equations, the following equations of 6 DOF motions are solved for predicting wave induced body motions:

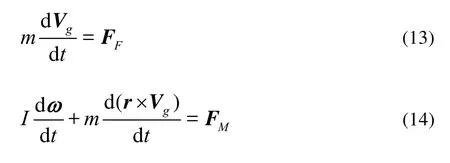
whereVgis the velocity of center of mass,ωthe angular velocity,mthe body mass,Ithe mass tensor of moment of inertia,FFandFMare the total forces and moments acting on the body center of mass:

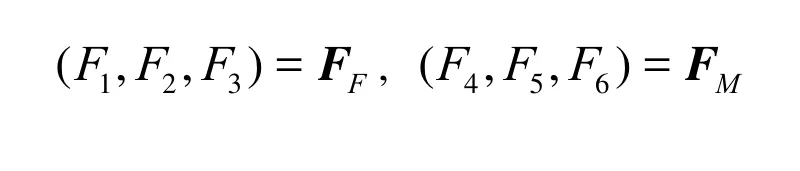
3. Solution procedures

The initial boundary value problems of Eqs.(2)-(7) can be solved by a Rankine panel method. According to Green’s second identity, the disturbed potential can be obtained by the following boundary integral equation:

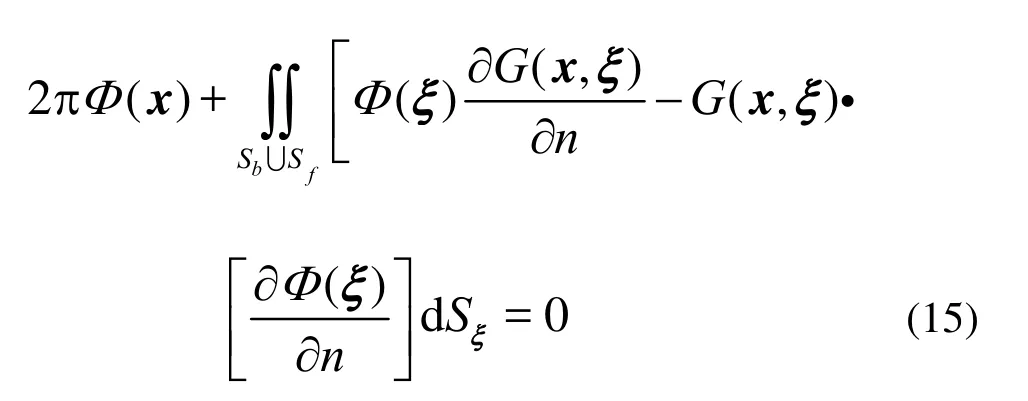
Though the Rankine panel method is very flexible to solve body-wave interaction problems, but the Rankine sourceG(x,ξ) does not satisfy any boundary conditions, so the partial free surface and body surface will be discretized with a distribution of the Rankine sources.

There are four unknowns in Eq.(15): the disturbed potentialΦ|Sband its normal derivativeΦn|Sbon body surfaceSb, the disturbed potentialΦ|Sfand its normal derivativeΦn|Sfon free surfaceSf.

Φn|Sbis calculated by using the body boundary condition (5), and the disturbed potentialΦ|Sfon partial free surface can be obtained by transforming the linear free surface conditions (3)-(4) into ordinary differential equations. Then the Eq.(15) can be rewritten as

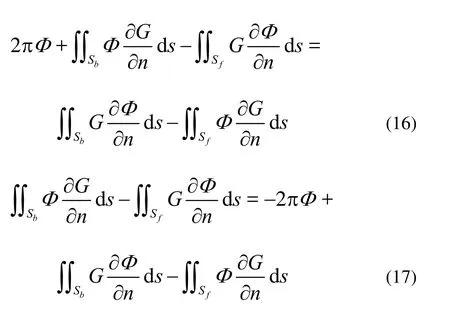
The Eqs.(16)-(17) are to be discretized into the linear equation system. The disturbed potentialΦ|Sband normal derivativeΦn|Sfare obtained by solving the linear system.

As the partial free surface is used, special approach must be adopted to satisfy the radiation condition. There are three typical methods for theradiation condition: the mixed-source formulations[15,17], numerical beach[13,14]and multitransmitting formula[18]. In this article, the numerical damping beach, which is simple and efficient, is employed for radiation condition. The Ordinary Differential Equations (ODEs) for solvingΦ|Sfand disturbed free surface elevationζcan be written as wherev(r) is the damping coefficient of numerical beach, andαdenotes the strength coefficient. The numerical beach is distributed over the free surface regionr0≤r≤L.

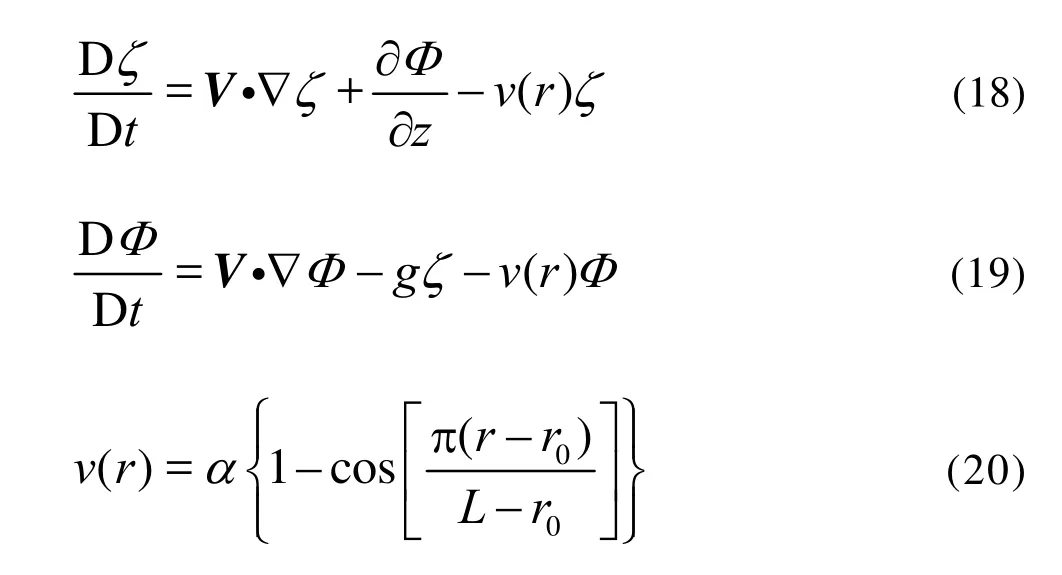
To obtain disturbed potentialΦ|Sfandζ, we employ the fourth-order Adams-Moulton numerical integrating method for solving the ODEs (18)-(19), onceΦn|SfandΦ|Sfhave been obtained.

The next step for the solution of wave-induced ship motions is to obtain hydrodynamics pressures over the body surface. According to Eq.(8), the partial time derivatives ofΦ|Sbon the body surface will be computed by using the following equation[13]:

The total forces and moments acting on body are obtained by integrating the pressure over the body surface according to Eq.(11). The Eqs.(13)-(14) of ship motions are solved by the fourth-order Runge-Kutta algorithm.

4. Numerical simulations and results

4.1Panel mesh

The partial free surface and hull surface of a ship are discretized into quadrilateral elements. The free surface is truncated at several ship lengths away from the ship center. We find that 3-5 ship length for free surface circular is rational by numerous numerical experiments. The sketch of free surface panel mesh is shown in Fig.1.

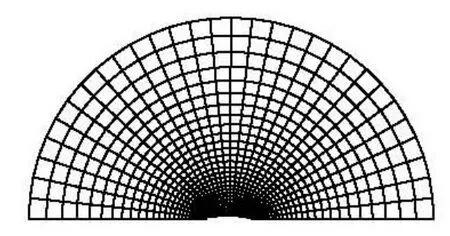
Fig.1 Sketch of free surface panels

To generate the hull panel mesh, we adopt the in-house code SHIPPAN developed by CSSRC. As a whole, the hull surface is complex, so we divide the hull surface into several logical quadrilaterals, such as bulbous bow, main hull, transom and bulb stern, etc.. The panels are generated on each of the logical quadrilaterals. A lot of numerical cases show that the SHIPPAN is effective and efficient for hull panel mesh.

4.2Incident wave

Wave-induced ship motions contain 6 degree of freedom: surge (x1), sway (x2), heave (x3), roll (x4), pitch (x5), yaw (x6). In this article, we only consider that the ships move in regular head waves, and are free to heave and pitch.

The incident head waves are described by linear wave theory in water of infinite depth, the incident wave potentialIΦand elevationηcan be written as

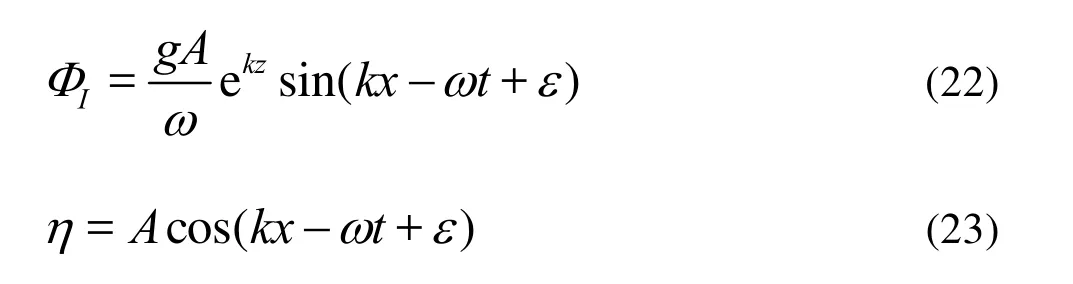
whereAdenotes the wave amplitude,kthe wave number, andωthe circular frequency.

The heave (x3) and pitch(x5) motions are nondimensionalized as

4.3 Numerical results

Numerical results for two ships are obtained by using the present method and compared to model test results for validation.

The principal particulars of DTMB5512 and 4000TEU container vessel are listed in Table 1.

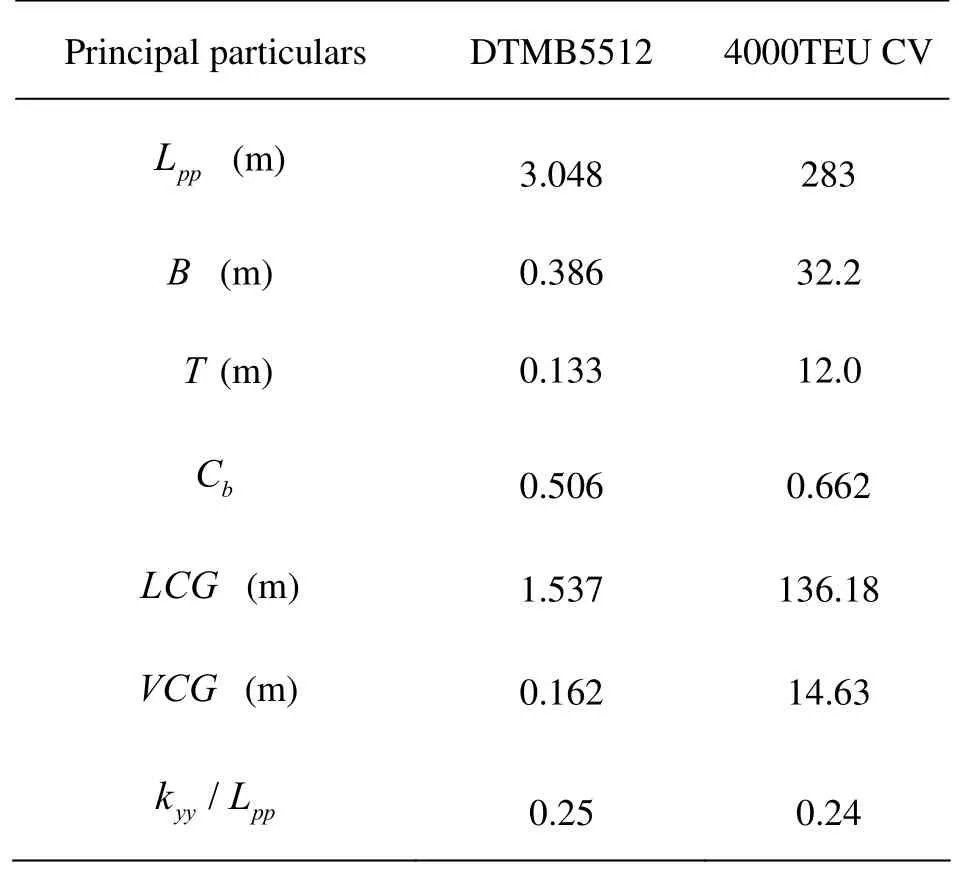
Table 1 Principal particulars of DTMB5512 and 4000TEU CV

4.3.1 DTMB5512

The towing tank experiments of coupled pitch and heave motions in regular head waves for DTMB5512 were conducted in the IIHR towing tank[19].

In the numerical simulations of DTMB5512, 30× 60panels are generated on free surface. Hull surface are divided into 8 logical quadrilaterals, and 1000 panels are used. Figure 2 shows the sketch of panel arrangement of DTMB5512.

Fig.2 Panel arrangement of DTMB5512

The numerical simulations of DTMB5512 were carried out in the incident wave of 0.0182 m amplitude, wave-lengthλvaried from (0.3-4)×Lpp, 16 wave-lengths were computed respectively with four speeds for which the corresponding Froude number were 0.0, 0.19, 0.28, 0.41.

The time histories of typical heave and pitch motions of DTMB5512 with different incident waves are presented in Figs.3 and 4. The Froude number is 0.28. The regular wave-lengthλare 0.5, 1.0, 2.0 timesLpprespectively.It can be seen that heave and pitch motions remain steady after several periods atλ/Lpp=1.0, 2.0. The heave and pitch motions are not regular forλ/Lpp=0.5, as the incident wave is of nonlinearity for 2A/λ>1/50. Therefore, the motions of ship are also of nonlinearity.

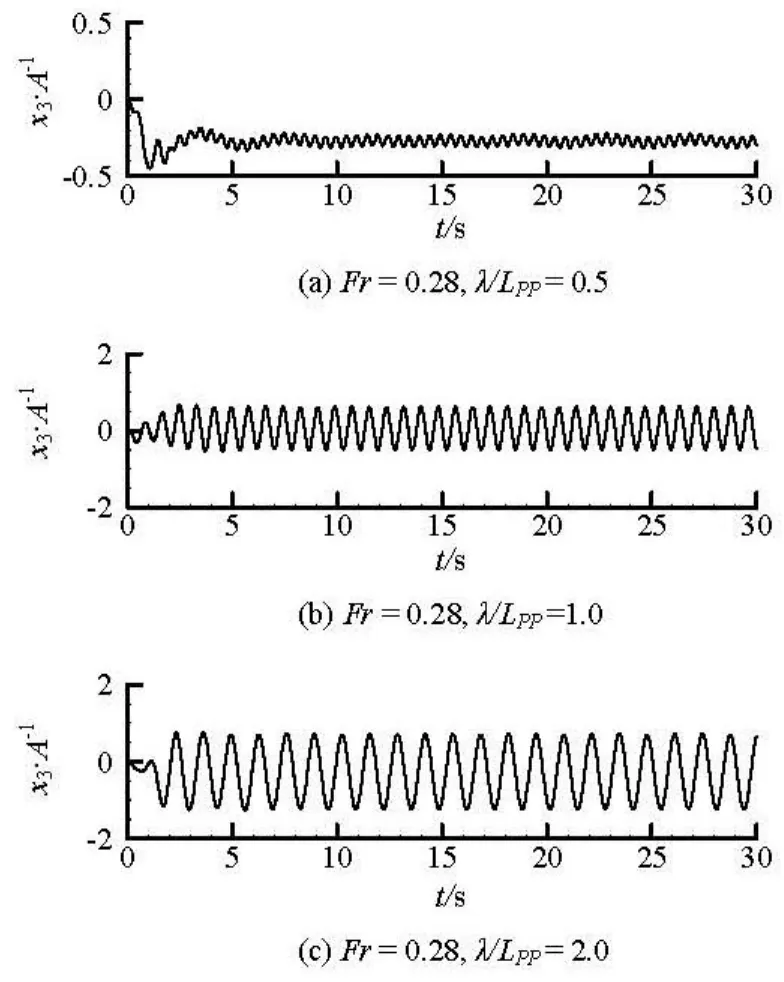
Fig.3 Time history of nondimensional heave motions

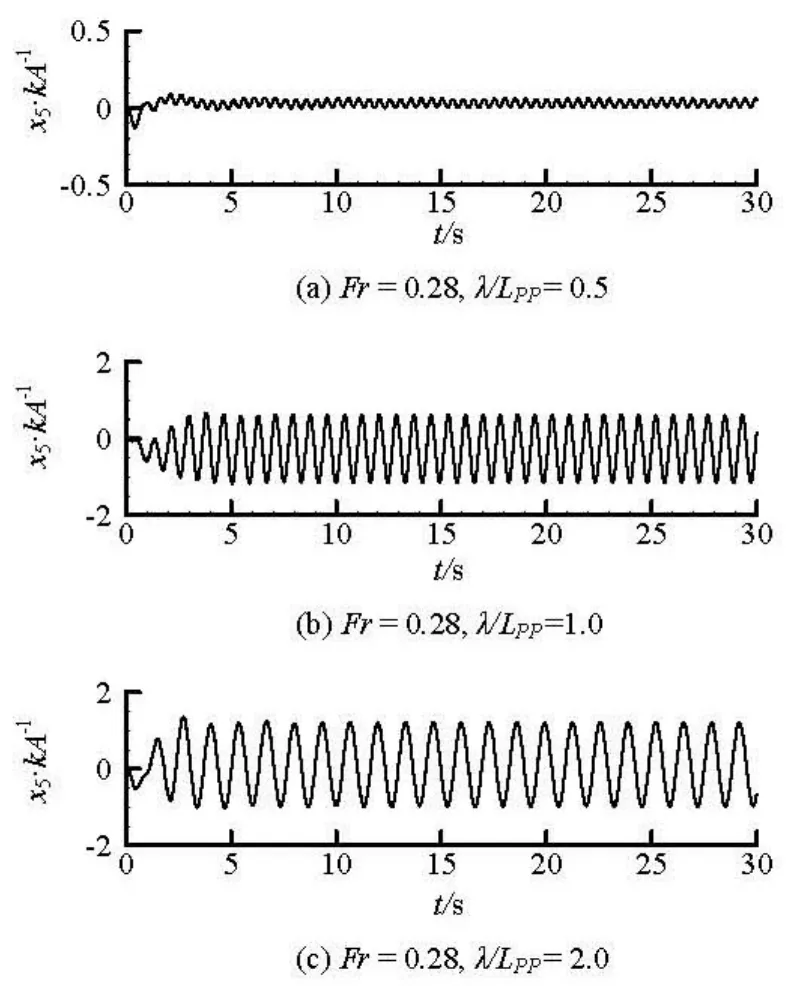
Fig.4 Time history of nondimensional pitch motions

To compare the results obtained from the present method with experimental results, the time histories of heave and pitch motions are transformed into heave and pitch transfer functions by using the Fast Frouier Transformation (FFT). The transfer functions of heave and pitch motions are also compared with the results of linear strip theory code Ship Motion Program(SMP). The detailed experimental data and the results of SMP are supplied by the IIHR on the website.

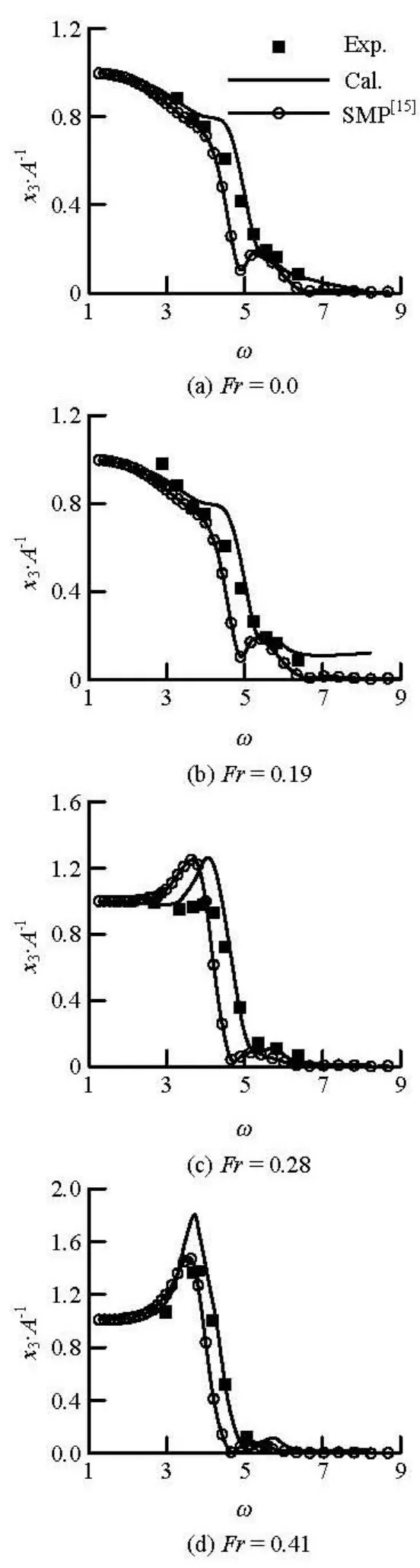
Fig.5 Heave transfer functions of DTMB5512

Figures 5 and 6 show the comparison of transfer functions of DTMB5512 with four forward speeds, in which the corresponding Froude number are 0.0, 0.19, 0.28, 0.41. Simulated results of SMP are also plotted in these figures. As a whole, the results of the present method agree well with the experimental data. The overestimate of heave motions at the peaks of transfer functions can be observed for higher Froude number, such as 0.28, 0.41. The present method employs linear theory, while nonlinear effects, such as, nonlinear Froude-Krylov force and body nonlinear are not taken into account. However, the results of the present method are better than those of SMP in amplitudes and phases.

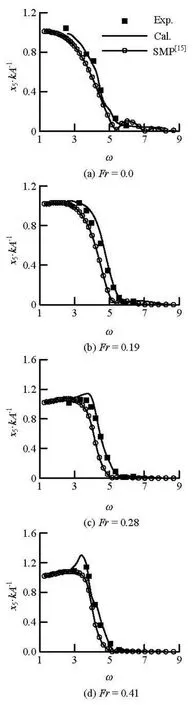
Fig.6 Pitch transfer functions of DTMB5512

4.3.2 4000TEU container vessel

The model test of 4000TEU container ship was conducted in the seakeeping basin of the CSSRC with the dimensions of 69 m×46 m×4 m (depth).

To carry out numerical simulations of 4000TEU container vessel, 30×60 panels were generated on the free surface. 2500 panels of 4000TEU container shipwith 8 logical quadrilaterals were adopted, and panel arrangement is shown in Fig.7.

Fig.7 Panel arrangement of 4000TEU CV

In numerical simulations of 4000TEU container vessel, the regular head waves were adopted as the incident wave , the wave-lengthλwere in the range from 0.3 to 4 timesLpp, and 16 wave-lengths were computed respectively with the wave amplitude of 2.83 m. The Froude number based onLppequals 0.234.

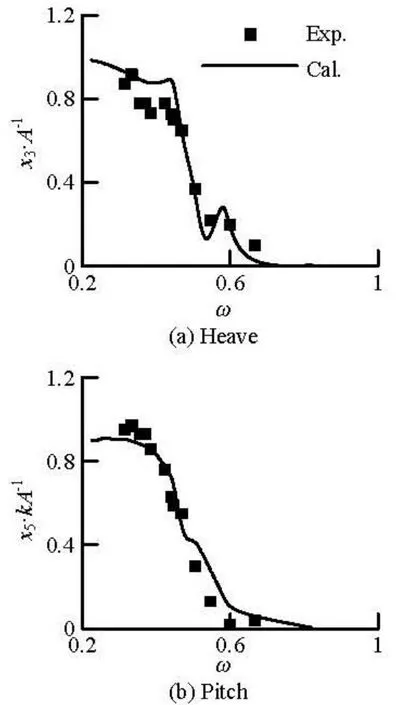
Fig.8 Heave and pitch transfer functions of 4000TEU container vessel

Figure 8 shows the comparisons of heave and pitch transfer functions of 4000TEU container vessel in regular waves with experimental data. The simulated results agree well with the experimental data. Though the pitch amplitudes of present method are over-predicted in the range from 0.5-0.7 of circular frequencyω. More nonlinear effects will be included in the present method to improve the simulated results.

The wave patterns of 4000 TEU CV atλ/Lpp=1.35are plotted in Fig.9. The interaction of incident wave and disturbed wave can be easily observed, and the relative motions of hull and wave surface can be obtained correspondingly by using the present method.

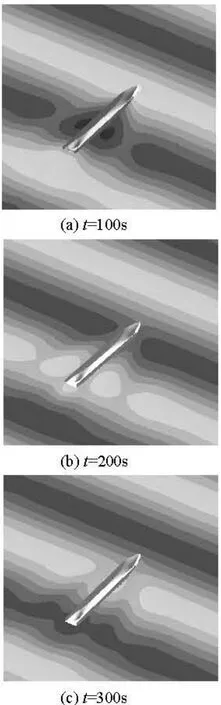
Fig.9 Wave patterns of 4000TEU CV forλ/Lpp=1.35

The time-cost of present method is very limited. For example, a simulation case of 4300 panels with time stept=0.1, the simulation time is about 20 min for 3000 steps on a 2.8G Hz PC. So, the present method is not only effective but also efficient in time-cost.

5. Concluding remarks

A Rankine panel method in time domain, which employs linear free surface conditions and mean wetted surface, has been developed to predict the wave-induced ship motions in regular head waves. The numerical damping beach is adopted for satisfying the radiation condition, and the equations of motions are solved with the 4th-order Runge-Kutta algorithm. The heave and pitch transfer functions of DTMB5512 are compared for the present method, experimental data and linear strip theory program SMP, and the agreement between the present method and experimental data is quite good. The results of the present method are closer to experimental data than those of the SMP. The simulated results of 4000TEU container vessel in regular waves are also compared with corresponding experimental data, the agreementis not bad. More nonlinear effects, such as, the nonlinear Froude-Krylov force and body nonlinearity will be taken into account to improve the prediction accuracy of the present method.

[1] BECK R. D., REED A. Modern seakeeping computations for ships[J].The 23rd Symposium on Naval Hydrodynamics. Valde Reuil, France, 2000.

[2] HU C. H., KASHIWAGI M. Validation of CIP-based method for strongly nonlinear wave-body interactions[C].The 26th Symposium on Naval Hydrodynamics.Rome, Italy, 2006.

[3] WU Cheng-sheng, ZHU De-xiang and GU Ming. N-S CFD simulation of wave-induced ship motions in regular head wave [J].Journal of Ship Mechanics,2008, 12(5): 692-696.

[4] CARRICA P. M., WILSON R. V. and NOACK R. et al. A dynamic overset single-phase Level-set approach for viscous ship flows and large amplitude motions and maneuvering[C].The 26th Symposium on Naval Hydrodynamics.Rome, Italy, 2006.

[5] SATO Y., ORIHARA H. and MIYATA H. Practical Application of two CFD codes for ship motions in arbitrary waves[C].The 26th Symposium on Naval Hydrodynamics.Rome, Italy, 2006.

[6] ZHU D. X., KATORY M. A time-domain prediction method of ship motions[J].Ocean Engineering,1998, 25(9): 781-791.

[7] SINGH S. P., SEN D. A comparative study on 3D wave load and pressure computations of different level of modelling of nonlinearities[J].Marine Structures, 2007, 20: 1-24.

[8] CHEN Zhi-jie, WANG Yong-xue and WANG Guo-yu et al. Time-domain response of immersing tunnel element under wave actions[J].Journal of Hydrodynamcs,2009, 21(6): 739-749.

[9] JANSON C. E. Potential flow panel methods for the calculation of free-surface with lift[D]. Ph. D. Thesis, Chalmers, Sweden: Chalmers University of Technology, 1997.

[10] RAVEN H. C. Inviscid calculations of ship wave making capablitities, limitations, and prospects[C].The 22nd Symposium on Naval Hydrodynamics.Washington DC., 1998.

[11] CHEN Jing-pu, ZHU De-xiang and LIU Xiao-dong. Study of numerical method for nonlinear ship wave making [J].Chinese Journal of Hydrodynamcs,2008, 23(4): 357-363(in Chinese).

[12] FERRANT P. Three-dimensional unsteady wave-body interactions by a Rankine boundary element method[J].Ship Technology Research,1993, 40(3): 165-175.

[13] KRING D. C., HUANG Y. F. and SCLAVOUNOS P. et al. Nonlinear ship motions and wave-induced loads by a Rankine method[C].Proc. 21st Symposium on Naval Hydrodynamics.Trondheim, Norway, 1996.

[14] HUANG Y. F., SCLAVOUNOS P. D. Nonlinear ship motions[J].Journal of Ship Research,1998, 42(2): 120-130.

[15] LIN W. M., ZHANG S. and WEEMS K. et al. A mixed source formulation for nonlinear ship-motion and wave-load simulations[C].Proceedings of the Seventh International Conference on Numerical Ship Hydrodynamics.Nantes, France, 1999.

[16] KIM K. H., KIM Y. H. On technical issues in the analysis of nonlinear ship motion and structural loads in waves by a time-domain Rankine panel method[C].The 23rd International Workshop on Water Waves and Floating Bodies.Jeju, Korea, 2008.

[17] DAI Y. Z., WU G. X. Time domain computation of large amplitude body motion with the mixed source formulation[C].The 8th International Conference on Hydrodynamics.Nantes, France, 2008.

[18] XU G., DUAN W. Y. Time domain simulation of irregular wave diffraction[C].The 8th International Conference on Hydrodynamics.Nantes, Grance, 2008.

[19] IRVINE M., LONGO J. and STERN F. Pitch and heave tests and uncertainty assessment for a surface combatant in regular head wave[J].Journal of Ship Research,2008, 52(2): 146-163.

October 20, 2009, Revised March 29, 2010)

*Biography:CHEN Jing-pu (1982-), Male, Ph. D. Candidate

2010,22(3):373-380

10.1016/S1001-6058(09)60067-6