NUMERICAL STUDY OF WALL WETTABILITIES AND TOPOGRAPHY ON DRAG REDUCTION EFFECT IN MICRO-CHANNEL FLOW BY LATTICE BOLTZMANN METHOD*

ZHANG Ren-liang, DI Qin-feng, WANG Xin-liang, GU Chun-yuan

Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University,Shanghai 200072, China Shanghai Key Laboratory of Mechanics in Energy and Environment Engineering, Shanghai 200072, China, E-mail: zhrleo@gmail.com

NUMERICAL STUDY OF WALL WETTABILITIES AND TOPOGRAPHY ON DRAG REDUCTION EFFECT IN MICRO-CHANNEL FLOW BY LATTICE BOLTZMANN METHOD*

ZHANG Ren-liang, DI Qin-feng, WANG Xin-liang, GU Chun-yuan

Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University,Shanghai 200072, China Shanghai Key Laboratory of Mechanics in Energy and Environment Engineering, Shanghai 200072, China, E-mail: zhrleo@gmail.com

The dynamics of two-phase flows with a constant driving force inside a micro-channel is studied by using the Lattice Boltzmann Method (LBM) and the Shan-Chen multiphase model in this article. Flow regimes under different wall wettabilities and over smooth and grooved geometric surfaces are investigated. It is found that flow behaviors are strongly affected by the wall wettability and topography. Our results show that the LBM is efficient and accurate, and has very good application prospect in the study of drag reduction of microscopic seepage of reservoir.

contact angle, wettability, miro-channel, multiphase-flow, Lattice Boltzmann Model (LBM)

1. Introduction

Water injection is the main means of improving oil recovery in low permeability oilfields, but in water flooding development, it mainly behaves with high injection pressure, low injection rate and so on. In order to exploit low permeability reservoir more efficiently, two methods have been used. One is thereservoir reconstruction method, such as acidification, hydraulic fracturing, which reduce drag by amplifying pore size, but the existing problem is that the reservoir may be contaminated if the method is in failure. The other is the surface modification method, which contains drag reductions by surfactant and by hydrophobic nanoparticles (HNPs). The latter is a new drag reduction technology to improve oil recovery in low permeability oilfields in reservoir micro-channels, which can decrease injection pressure and enhance water injection volume. The HNPs are adsorbed by the wall and then a strong- or super-hydrophobic layer is formed, which could lead to a slip boundary condition and decrease drag on the fluid. This mechanism has been modified via lab tests and simulation method by Di et al.[1], but the effects of wall wettabilities and topography on micro-channel flow should be intensively studied.

Droplet motion is a key element of a wide variety of phenomena encountered in technical applications,such as impact of droplet[2,3], which is used to investigate painting, injection in combustors, ink-jet printing[4]and cooling the hot surface[5], the spreading of mesoscale droplets on homogeneous and heterogeneous surfaces[6], which is used to investigate wetting properties of underlying substrate, and droplet formation[7], which is used to investigate interaction between immiscible fluids. Simulation of the evolution of fluid interface is a challenging problem for both the Lattice Boltzmann Method (LBM) and other conventional CFD techniques, because any phase interface boundary is mesoscopic by nature.

Numerical methods can be very instrumental in enhancing understanding of fluid behavior, the LBM is a promising tool to simulate the incompressible viscous flows[8]. Unlike the traditional CFD, the LBM is based on microscopic models and mesoscopic kinetic equations. The LBM recovers the Navier-Stokes equations in the incompressible flow limit. The LBM can be considered as a mesoscopic approach, lying in between microscopic molecular dynamics and conventional macroscopic fluid dynamics. It does not solve the differential equations, but only involves a series of collision and stream steps. More importantly, it is relatively easy to set the non-slip boundary condition for systems with complex geometry and there are a couple of free surface models[9]developed for simulating the moving interface between immiscible gas and liquid fluids. An alternative solution is the Shan-Chen multiphase model[10,11], which can be useful in treating problems involving surface tension, capillarity and phase transition in multiphase multi-component systems.

In this work, we simulate droplet moving in micro-channel to investigate the effects of wall wettabilities and topography on drag reduction. With a general bounce-back no-slip boundary condition applied to the interface between fluids and solid surfaces, together with the Shan-Chen multiphase model, the LBM is used to simulate the liquid-phase flow inside micro-channels with different wall wettabilities and topography.

2. Numerical model

2.1 The LBGK model

The LBM, which involves a single relaxation time in the Bhatnagar-Gross-Krook (BGK) collision operator[12], is used here. The time evolution of this model can be written as

where c=Δx/Δt is the lattice velocity, Δx the lattice distance, and Δt the time step of simulation.

The mass density ρ and momentum density ρu of the fluid are calculated from the first and second moments of the distribution function, i.e.,

And the relaxation time tunes the kinematic viscosity as

The non-slip boundary condition at solid-fluid interfaces is realized by the bounce-back rule, where the momentum of the fluid particles that meet a solid wall is simply reversed. The bounce-back rule is simple and computationally efficient, and enables fluid flow simulations in complex geometries. On the inlet and outlet boundaries, the periodic boundary conditions are used.

2.2Shan-Chen multiphase model

To simulate non-ideal multiphase fluids, the attractive or repulsive interaction among molecules, which is referred to as the non-ideal interaction, should be included in the LBM. There are many approaches to incorporate non-ideal interactions, such as the color-fluid model, interparticle-potential model, free-energy model, mean-field theory model and so on. The interparticle-potential model proposed by Shan and Chen is to mimic microscopic interaction forces between the fluid components. This model modified the collision operator by using an equilibrium velocity that includes an interactive force. This force guarantees phase separation and introduces surface-tension effects[9].

This model has been applied with considerable success in measuring contact angles and porous flow[13]. As an extension of the Shan-Chen model, Benzi et al.[14]derived an analytical expression for the contact angle and for surface energy between any two of the liquid, solid and vapor phases. Because of spurious velocities, it is difficult for most LBM schemes to deal with two phases with a high density ratio. It has been found that highly isotropic gradient operators are able to reduce the spurious velocities[15]and Yuan and Schaefer proposed to modify the EOS, and thus one can reach density ratios higher than 1000:1 with the simulation still stable[16].

In the Shan-Chen multiphase model, the non-ideal interaction is obtained via using an attractive short-range force

Adhesive forces between the fluid and solid phases are modeled by introducing an extra force

s=0, 1 for the fluid and the solid phase, respectively, the interaction strengthGis used to control the two-phase liquid interaction, and adhesion parameterGadsis used to control the wettability behavior of the liquid at solid surfaces.

ψ(x,t) is a local “effective mass”[10,11,17,18], which is defined as

Using these definitions, the fluid momentum is changed at each time step according to

whereu′ is the new fluid velocity. The equation of state in the Shan-Chen model is[18]

3. Results and discussion

3.1Contact angle simulation

The LBM simulations were carried out in a 2-D domain. The grid mesh used is 50×100. In the simulation, the general non-slip bounce-back schemewas employed for the solid-fluid interfaces, and periodic boundary conditions were applied in the horizontal direction (the same below). A droplet, with the diameter of 30 is set in the middle of the lower boundary. After 3×104time steps (in our simulations the units are lattice units as Ref.[18], the same as below), it tends to be stabilized, because it runs other more time steps, it has the same status. Figure 1 shows an example of the static contact angle, which is 135owhenG=−120,Gads=−100 andψ(x,t)=4e−200/ρin Eqs.(9) and (10). It is further found that the contact angle of droplet at the lower boundary varies from 0 degree to 180owith changing adhesion parameterGads. (see in Fig.2)

Fig.1 Static contact angle

As is shown in Fig.2, the contact angle is proportional to the adhesion parameters, and hence we can change adhesion parameters to simulate arbitrary contact angle, and then obtain different wall wettabilities.

Fig.2 Contact angle as a function ofGadsforG=−120

Fig.3 Initial conditions

3.2Effects of wall wettability

The initial condition is illustrated in Fig.3. The grid mesh used is 66×400 and the size of the liquid segment is 50×60. The darkest part represents the liquid, the lightest parts represent the gas, and the parts with in-between darkness represent the solid walls (the same as below). ChangingNf, we can get different grooved surface, and asNf=0, it can be considered as smoothed surface.

In engineering applications, surfactants are often injected into the micro-channel to change the wall wettalility and to reduce the interfacial tension between wall and water[19]. In the simulation of a droplet moving inside a smooth channel, the parameters areG=−120 ,ψ(x,t)=4e−200/ρ,Nh=8,Nw=2, andNf=0, the different wall wettabilities are easily achiwved by changing the adhesion parameterGads. In the simulations, the wettabilities of the walls (upper and lower) were set as hydrophilic (with the contact angle of 68o), neutral wetting (with the contact angle of 90o), and hydrophobic (with the contact angles of 108oand 129o), respectively. The simulations were run to 1×104time steps when static equilibrium was nearly attained. After 1×104time steps, body-force was applied in the flow direction (this method has been used in Ref. [18]).

Fig.4 The average liquid velocity under different wettabilities of the wall

Figure 4 gives the comparison of the average liquid velocity under different wettabilities of the wall. There are four cases for the evolution processes of droplet velocity. The droplet moves faster on the wall surface in the more hydrophobic case, i.e., the wettabilities have great effects on the flow. The more hydrophobic the wall is, the faster the flow rate is, and then the more remarkable the drag reduction effect is.

3.3Effect of smooth and grooved surface

In this section the droplets moving inside a micro-channel with a smooth surface and a grooved

surface are simulated, and the parameters areNh=8,Nw=2,Nf=3 for grooved surface andNh=8,Nw=2,Nf=0 for smoothed surface respectively. The wettability of the wall is set to be hydrophilic (with the contact angle of 68o) or hydrophobic (with the contact angle of 129o). In both cases, the simulations were run to 1×104time steps till the static equilibrium os nearly attained. After 1×104time steps, body-force is applied in the flow direction.

The average liquid velocity under different wettabilities of the lower wall is shown in Figs.5 and 6. When the surface of lower wall is hydrophobic, the average velocity of fluid flowing in the grooved surface wall is higher than that in the smooth surface, and when the wettability of lower wall is hydrophilic, it is opposite.

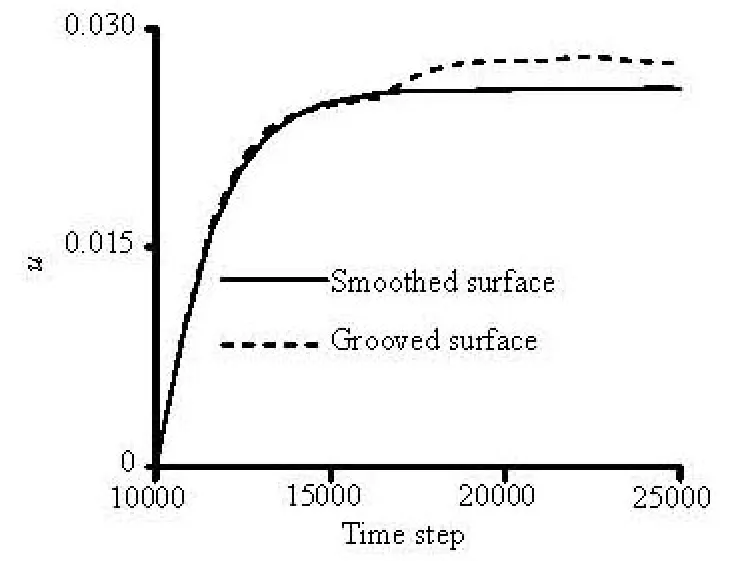
Fig.5 The average liquid velocity under smooth and grooved hydrophobic surfaces

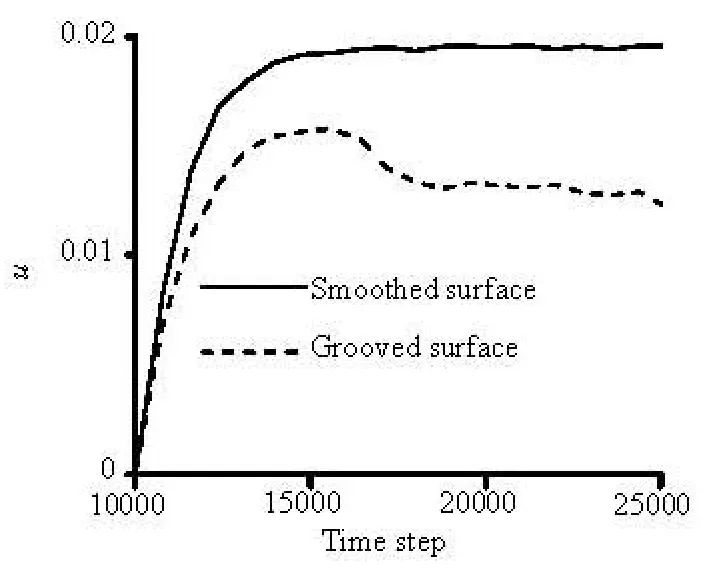
Fig.6 The average liquid velocity under smooth and grooved hydrophilic surfaces

3.4Effects of roughness

Studies[20]have shown that the inorganic nanoparticles modified by weak hydrophobic material could have strong hydrophobic property. In this section we simulate a droplet moving inside a grooved channel in a 2-D domain, the parameters areG=−120 ,ψ(x,t)=4e−200/ρ,Nh=8,Nw=2, and the distance between neighboring nanoparticles,Nf, is changed to be 5,11,17 and 22 respectively. In the simulation, nanoparticles’ intrinsic contact angle is 108o. Figure 7 shows the comparison of snapshots of the liquid positions and configurations every 5000 time steps for the four cases.

From the image sequences we can see that the presence of grain spacing alters the droplet dynamics properties. When the grain spacing changes from 5 to 17, the droplet speed increases, but when grain spacing reaches to 22, the droplet speed decreases greatly. This also can be seen from Fig.8. From Fig.7 we can also see that when the grain spacing changes from 5 to 17, the droplet does not contact the bottom but when the grain spacing reaches to 22 the droplet contacts the bottom.

A general trend shown in Fig.8 is that in each case the time series of the average liquid velocity are similar to those of a cosine curve when grain spacing is 5 to 17, and we also can see that, when the grain spacing is wider, the average liquid velocity is higher, the frequency of the curve is lower and the amplitude of the curve is greater. This may be due to the fact that a non-continuous solid-liquid contact line in the roughness wall is made by the gas trapped by nano-structured boundary. When the solid-liquid contact line is continuous the liquid velocity is lower, and when the solid-liquid contact line is non-continuous the liquid velocity is higher. It also can be seen from Fig.8 that the speed of the droplet varies with the grain spacing. There is a critical grain distance. When the grain spacing is smaller than the critical distance (as shown in Fig.8, grain spacing is between 5 and 17), the average liquid velocity increases as the distance between nanoparticles increases, this may be due to the fact that when the distance between neighboring nanoparticles is wider, more gas will be trapped by the nano-structured and the solid-liquid contact line will become shorter, which will make the drag on the droplet decrease. When grain spacing is more than the critical distance such as 22 lattice unit, the droplet will contact the bottom and the average liquid velocity will decrease greatly.

4. Conclusion

Fig.7 Comparison of snapshots of the liquid positions and configurations

In summary, a droplet with a constant driving force moving inside a micro-channel has been studied by using an LBM and the Shan-Chen multiphase model. It is found that the droplet can move faster with higher contact angle on smooth hydrophobic surfaces and the drag on the droplet is smaller on the grooved surface than that on the surface when the wettability of the wall is hydrophobic, but when the wettability of the wall is hydrophilic, the situation is opposite. Roughness can make hydrophobic wall more hydrophobic and make hydrophilic wall more hydrophilic. It is also found that the drag on the droplet is strongly affected by the wall wettability and roughness when the system scale is small. These results and findings would probably be helpful for seeking some insights into the drag reduction and also into the multiphase flows in micro machines.

Fig.8 Comparison of the average liquid velocity under different grain spacing

[1] DI Qin-feng, SHEN Chen and WANG Zhang-hong et al. Experimental research on drag reduction of flow in micro-channels of rocks using nano-particle adsorption method[J].Acta Petrolei Sinica,2009, 30(1): 125-128 (in Chinese).

[2] HYVALUOMA J., RAISKINMAKI P. and JASBERG A. et al. Simulation of liquid penetration in paper[J].Physical Review E,2006, 73(3): 036705-1-036705-8.

[3] SHI Zi-yuan, YAN Yong-hua and YANG Fan et al. A lattice Boltzmann method for simulation of a three-dimensional drop impact on a liquid film[J].Journal of Hydrodynamics,2008, 20(3): 267-272.

[4] Van DAM D. B., LE CLERC C. Experimental study of the impact of an ink-jet printed droplet on a solid substrate[J].Physics of Fluids,2004, 16(9): 3403-3414.

[5] GUO Jia-hong, DAI Shi-qiang. Research on stability of liquid film on hot solid surface impinged by small droplets[J].Journal of Hydrodynamics,Ser. B,2007, 19(3): 264-271.

[6] DUPUIS A., YEOMANS J. M. Modeling droplets on superhydrophobic surfaces: Equilibrium states and transitions[J].Langmuir,2005, 21(6): 2624-2629.

[7] KIM L. S., JEONG H. K. and HA M. Y. et al. Numerical simulation of droplet formation in a micro-channel using the lattice Boltzmann method[J].Journal of Mechanical Science and Technology,2008, 22(4): 770-779.

[8] CHEN S., DOOLEN G. D. Lattice Boltzmann method for fluid flows[J].Annual Review of Fluid Mechanics,1998, 30(1): 329-364.

[9] AIDUN C. K., CLAUSEN J. R. Lattice Boltzmann method for complex flows[J].Annual Review of Fluid Mechanics,42(1): 439-472.

[10] SHAN Xiao-wen, CHEN Hu-dong. Lattice Boltzmann model for simulating flows with multiple phases and components[J].Physical Review E,1993, 47(3): 1815-1819.

[11] SHAN Xiao-wen and CHEN Hu-dong. Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation[J].Physical Review E,1994, 49(4): 2941-2948.

[12] QIAN Yue-hong, HUMIERES D. D'. and LALLEMAND P. Lattice BGK models for Navier-Stokes equation[J].Europhysics Letters,1992, 17(6): 479-484.

[13] HUANG Haibo, THORNE D. T. Jr and SCHAAP M. G. et al. Proposed approximation for contact angles in Shan-and-Chen-type multicomponent multiphase lattice Boltzmann models[J].Physical Review E,2007, 76(6): 066701-1-066701-6.

[14] BENZI R., BIFERALE L. and SBRAGAGLIA M. et al. Mesoscopic modeling of a two-phase flow in thepresence of boundaries: The contact angle[J].Physical Review E,2006, 74(2): 1509-1-1509-14.

[15] SHAN X. W. Analysis and reduction of the spurious current in a class of multiphase lattice Boltzmann models[J].Physical Review E,2006, 73(4): 7701-1-7701-4.

[16] YUAN P., SCHAEFER L. Equations of state in a lattice Boltzmann model[J].Physics of Fluids,2006, 18(4): 42101-1-42101-11.

[17] QIAN Yue-hong, SUCCI S. and ORSZAG S. A. Recent advances in lattice Boltzmann computing[J].Ann. Rev. comp. Phys.,1995, (3): 195-242.

[18] SUKOP M. C.Lattice Boltzmann modeling: an introduction for geoscientists and engineers[M]. 2006, Berlin: Springer.

[19] YIN Dai-yin, PU Hui. Numerical simulation study on surfactant flooding for low permeability oilfield in the condition of threshold pressure[J].Journal of Hydrodynamics,2008, 20(4): 492-498.

[20] GU Chun-yuan, DI Qin-feng and SHI Li-yi et al. Experimental investigation of superhydrophobic properties of the surface constructed by nanoparticles[J].Acta Physica Sinica,2008, 57(5): 3071-3076(in Chinese).

October 12, 2009, Revised March 3, 2010)

* Project supported by the National Natural Science Foundation of China (Grant No. 50874071), the National High Technology Research and Development Program of China (863 Program, Grant No. 2008AA06Z201), the Program of Science and Technology Commission of Shanghai Municipality (Grant No. 071605102), the project of Shanghai Education Commission Research Innovation (Grand No. 08ZZ45), the Program for Changjiang Scholars and Innovative Research Team in Universities (Grant No. IRT0844), and the China Postdoctoral Science Foundation (Grant No. 20090450687).

Biography:ZHANG Ren-liang (1982-), Male, Ph. D. Candidate

DI Qin-feng, qinfengd@sina.com

2010,22(3):366-372

10.1016/S1001-6058(09)60066-4