INTERANNUAL VARIABILITY OF KUROSHIO CURRENT AND ITS EFFECT ON THE NEARSHORE BRANCH IN JAPAN/EAST SEA*

ZHENG Pei-nan

Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, China

Marine Environmental Ensuring Center, the Headquarters of General Staff, Beijing 100081, China,

E-mail: zhengpeinan@ouc.edu.cn

WU De-xing, LIN Xiao-pei

Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, China

LI Xiao-ting

Marine Environmental Ensuring Center, the Headquarters of General Staff, Beijing 100081, China

INTERANNUAL VARIABILITY OF KUROSHIO CURRENT AND ITS EFFECT ON THE NEARSHORE BRANCH IN JAPAN/EAST SEA*

ZHENG Pei-nan

Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, China

Marine Environmental Ensuring Center, the Headquarters of General Staff, Beijing 100081, China,

E-mail: zhengpeinan@ouc.edu.cn

WU De-xing, LIN Xiao-pei

Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, China

LI Xiao-ting

Marine Environmental Ensuring Center, the Headquarters of General Staff, Beijing 100081, China

Based on the Hybrid Coordinate Ocean Model (HYCOM), this article presents simulations of the three-dimensional dynamic and thermal structure of the North Pacific Ocean (NPO) in the time domain from January 1991 to December 2000. The baroclinic current field and its interannual variability in Northwest Pacific Ocean (NWPO), especially, the Kuroshio Current (KC) and the Japan/East Sea (JES) are analyzed and discussed. The results show that the HYCOM covers a complete dynamic and thermo process with adequate representations of the eddy fields and variability in main spatial and temporal scales. The model is used to simulate the strong interanual variability of the KC, which may affect the strength of the eastern bifurcation of the Tsushima Warm Current (TSWC), named the Nearshore Branch (NB) in the JES. When the KC is strong and its axis is close to the Japan Island, the TSWC and its bifurcations in the JES would intensify accordingly. Our results confirm once again the hypothesis of Yang et al. that the KC determines the annual mean NB in the JES via the “island integral constraint”. This article further extends this hypothesis to study the KC role in the NB on a time dependent scale.

KC, JES, NB, HYCOM, interannual variability, island integral constraint

1. Introduction

The KC, the western boundary current of the

wind-driven subtropical gyre in the NPO, flows along the continental slope off the NWPO before it meets the Oyashio Current, its counterpart in the subpolar basin, off the east coast of Japan, from where it is separated from the western boundary to rejoin the interior Sverdrup flow. Along its pathway, several KC branches intrude the NWPO. For instance, the flow from the East China and Yellow Seas into the JES through Tsushima (or Korea) Strait – the TSWC – is widely believed to be a branch current of the KC. The KC and the NWPO interact over a broad scale, with rich dynamics issues, with respect to responses to changes in the forcing field associated with climate.

The TSWC carries warm and saline water into the JES with a transport around 2 Sv - 3 Sv (1 Sv =106m3s-1), about one tenth of the KC transport[1]. Once the TSWC enters the JES, it bifurcates into two boundary currents flowing along the Korean and Japanese coasts: a western branch along the Korean coast, widely referred to as the East Korean Warm Current (EKWC), and an eastern branch along the Japanese coast, commonly called the NB (Fig.1 for a schematic diagram of major flows in and around the JES). Some studies suggested the existence of a third branch, which locates offshore of the eastern branch and thus is often called the Offshore Branch (OB)[2, 3].

Holloway et al.[4]suggested that the pressure difference between the NPO and the JES drives the TSWC. More recent studies[5,6]show that the TSWC inflow and the Tsugaru Strait outflow vary in phase in seasonal and longer time scales. Furthermore, Spall[2]suggested that the Tsushima inflow and the Tsugaru outflow are driven by the pressure differences between two straits.

Yang[7]used the “Island Integral Constraints” to study the Taiwan Warm Current against the wind. It was believed that the pressure gradient (Δp) between the southern and the northern straits forces the northward flow. The integration of the momentum equation along the Taiwan’s east coast shows that there must be a pressure difference between the southern and the northern tips of the Taiwan Island to account for the considerable friction exerted by the mighty KC. This same pressure difference is also felt on the other side of the island where the northward flow is forced through the Taiwan Strait. It is found that the KC is the main forcing agent in the subtropical East Asian marginal seas. As it flows along the continental slope off the NWPO, the KC is responsible for the Δpbetween the upstream and downstream, which could be balanced by the bottom friction and the lateral friction of the island along the KC path. But the above study is based on a simple model in the steady state, and three dimensional effects with time variations are not considered.

The Japan Island is similar to the Taiwan Island. The strong western boundary current – the KC, flows northward along its east coast, and the NB flows northward along the other coast. In this study, we will investigate one aspect of this complex interaction by focusing on the KC’s role in establishing the NB in the JES and its dynamical consequences in a 10 year’s time scale. The “Island Integral Constraint” is used to explain the variation of the NB in the interannual time scale.

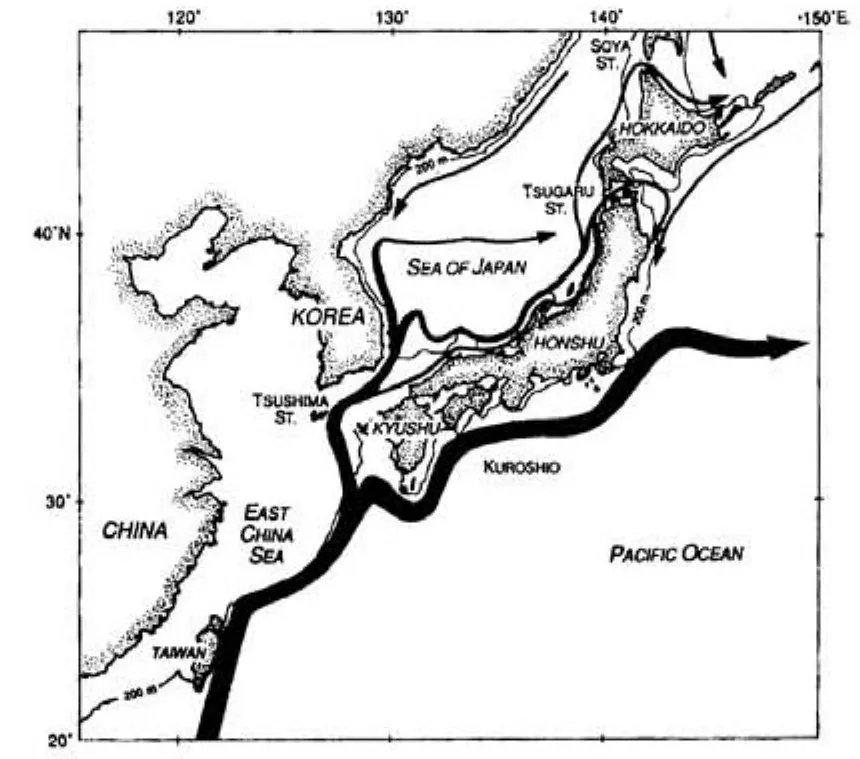
Fig.1 The schematic diagram of major oceanic currents in and around the Japan/East Sea (From Spall[2])

The article is organized as follows. The model, the bathymetry and the forcing field are presented in Section 2, and the model validation with the investigations and the atlas are given in Section 3. The results are analyzed and discussed in Section 4. Further discussions and a brief summary are given in Section 5.

2. Model and forcing fields

There are many studies of the KC based on field observations[8,9]and model simulations[5,10], which provide important information on the KC and its variations. But they do not cover the interannual time scales, and the model with a single vertical coordinate and the forced KC using the opening boundary condition may not well reflect some aspects of the KC. The model boundaries in this article are set far away from the KC and the JES, and the flexible vertical hybrid coordinates (Z, sigma and isopycnal) are used to better simulate the baroclinic process in the ocean. This configuration may better reflect many aspects of the KC than using just the KC transport as the opening boundary condition[11].

The numerical model used in this study is the latest version 2.1.34 of the HYCOM, which is a general circulation model based on a primitive equation with vertical coordinates that remain isopycnic in the open and stratified ocean. The isopycnal vertical coordinates are smoothly transformed toz-coordinates in a weakly stratified upper-ocean mixed layer, to terrain-following sigma coordinates in shallow water regions, and back toz-level coordinates in very shallow water. The latter transformation prevents layers from becoming too thin in very shallow water. The use of these coordinates can make simulations better adjusted to the real ocean stratification and topography[11,12].

The model domain covers Pacific Oceans from20.0oS to 48oN in latitude and from 100oE to 270oE in longitude (see Fig.2).

Fig.2 The model domain and bathymetry

The horizontal coordinate used here is Mercator, with resolution of 1/6°×1/6°×cosθ(withθbeing latitude) in longitude and latitude, respectively. 20 isopycnal vertical coordinates with a finer resolution in the upper layers are adopted. The topography used in the model is obtained by interpolated data from the ETOP2 (2 min gridded elevation data) bathymetry database[5], with the minimum and the maximum depth of 10 m and 5500 m, respectively. Because we are more interested in the upper ocean process, the sea surface pressure is used as the reference and the isopycnal vertical coordinates are 17.00, 18.50, 19.75, 20.75, 21.50, 22.50, 23.25, 24.00, 24.70, 25.75, 26.18, 26.52, 26.80, 27.03, 27.22, 27.38, 27.52, 27.64, 27.74 and 27.82. The reference densities of the first 7 layers are less than any sea water, which makes these 7 layers fixed on the sea surface, for the precision of the mixing layer[11]. The National Center for Environmental Prediction (NCEP) monthly mean data[13]are used for the surface boundary conditions from January in 1991 to December in 2000. The sea surface temperature, solid long wave radiation, solid short wave radiation, humidity, evaporation and precipitation are included. The temperature and salinity in the model are initialized by using the monthly-mean climatology compiled by WOA2005[5]. The Yellow River and the Yangtze River runoff are included as the fresh water flux. Vertical mixing and viscosity are calculated by the K-Profile Parameterization[14], because it provides mixing throughout the water column with a transition between the vigorous mixing in the surface boundary layer and the weaker diapycnal mixing in the ocean interior. The open boundaries are set at southern and northern boundaries. The eastern and western boundaries are set to be solid boundaries. At the lateral open boundaries, the sea level elevation is calculated as a superposition of the inverse barometric effect, dynamic height and river discharge effect. The model is then driven by inflows and outflows adjusted to the boundary sea level height, as is calculated from the time evolving boundary values of the temperature and salinity. At lateral solid boundaries, non-slip velocity and non-normal-flux tracer conditions are imposed[11]. The barotropic time step is set to 30 s, thus the baroclinic time step is set to 900s. After the model spin-up, the calculations are carried out for the hydroand thermodynamic parameters continuously for the time period from January 1991 to December 2000.

3. Model validations

Before the model results are used for analysis, they are compared with the investigations and the atlas.

Firstly we compare the upper layer (0 m-10 m) mean temperature between the model results in the interannual mean from 1991 to 2000 and the WOA05 annual mean data. Figure 3 shows that the model result is in good agreement with the WOA05 data. The higher sea temperature is located in the tropical West Pacific Ocean with the maximum of about 30oC.

Fig.3 The comparison of upper layer (10 m) temperature between the WOA05 and the model results in the interannual mean

Figure 4 shows the mean velocity field in the upper layer. The main currents in the NWPO may be seen from the figure, which were much studied and discussed by previous studies. The KC flows northeastward along the isobaths in the East China Sea and turns eastward at the south of Japan. At the southwest of Kyushu, one branch current flows into the Tsushima Strait, and acts as the origin of the TSWC. The model results are similar to those obtained by Spall[2]. We can also see the other currents in this area, such as the northward Yellow Sea Warm Current and the Taiwan Warm current, the southward Korean Coastal Current, and the China mainland coast current.

Fig.4 The mean velocity field in the upper layer of NWPO from model results

Figure 5 shows the volume transport of the TSWC and its branches at 34.5oN section. It is shown that the volume transport of the TSWC is large in summer and small in winter, and the two branches share similar patterns. One can also find double peaks in Fig.5, as reported by Takikawa[15]. The range of the TSWC transport is 1.5 Sv - 4.3 Sv, which agrees well with previous studies[3,15]. The average transport of the TSWC is about 2.7 Sv, that in the west channel is about 1.8 Sv, more than 60% of the transport of the TSWC and that in the east channel is about 0.9 Sv, less than 40% of the transport of the TSWC, a trend similar to previous studies[15].

Fig.5 The volume transports of the model results at 34.5oN section, in west channel and east channel

The above comparisons validate the simulations based on the NPO numerical model.

4. Analysis and discussion

4.1The interannual variability of the KC

Figure 6(a) shows the annual axis of the KC in the NWPO in simulations of a 10 years time scale. It is shown that the KC mainly flows along the shelf slope, but its path indicates several patterns, especially, in the south of Japan. Dong et al.[16-18]studied the bimodality of the Kuroshio with nonlinear numerical models, and they found that local forcing is the key factor in the bimodality of the Kuroshio, and the current velocity is important to the formation of large meander. By using the sea level data, Kawabe[19]found that there are three typical paths in the Tokara Strait south of Kyushu. They are the nearshore non-large-meander (nNLM) path, the offshore Non-Large-Meander (oNLM) path and the Large Meander (LM) path (see Fig.6(b)). With a two-layer primitive-equation model of the NPO driven by observed climatologically surface wind data, Qiu[20]found that the KC path at the south of Japan oscillates interannually between Non-Large-Meander (NLM) path state and LM state. His study suggested that the KC path variation may not be determined by the upstream inflow and can be explained by a self-sustained internal mechanism.

Fig.6 The axis of the KC in the NWPO in annual mean

4.2The interannual variability of the NB and its effect

on the KC

There were many studies related to the NB, from data analysis[15,21]to model simulation[22,23]. It is believed that the NB is mainly topographically controlled. The volume transports of the TSWC and its branches are discussed in section 3. It is shown that there are good correlations between the TSWC (especially its eastern branch, the NB) and the KC, which flows northward along the west coast of theJapan Island. In this article, we limit our attention to two situations (NLM and LM). In order to obtain some direct pictures, we draw the current fields in the mixing layer under NLM and LM types of the KC in the JES area (see Fig.7).

Fig.7 Current fields in mixing layer under two types of the KC in the JES area

Figure 7 shows that when the KC is stronger and flows closer to the east coast of Japan Island (in NLM type), the NB is intensified, when the KC is under the LM state, the NB is weak. So our hypothesis is: the location excursion of the KC axis could influence the NB significantly.

In order to verify our hypothesis, we calculate the volume transports both for the KC at the south of Japan and for the NB (the section locations are set at the black solid line shown in Fig.6(a)), as shown in Fig.8. This figure shows that the KC and the NB have a similar distribution against time. This volume transport distribution agrees with the pattern of the current fields shown in Fig.7. It confirms that the variable of the KC paths could affect the volume transports of the NB in the JES.

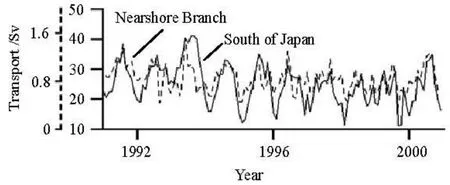
Fig.8 Volume transports between the KC at south of Japan and the NB

The “island integral constraint” has been used to explain various phenomena around islands and ridges, and is explained briefly here. For flows around an island, the velocity perpendicular to the boundary vanishes and thus the Coriolis force becomes zero in the momentum equation for the along-boundary flow. The integration of the momentum equation yields a simple balance:

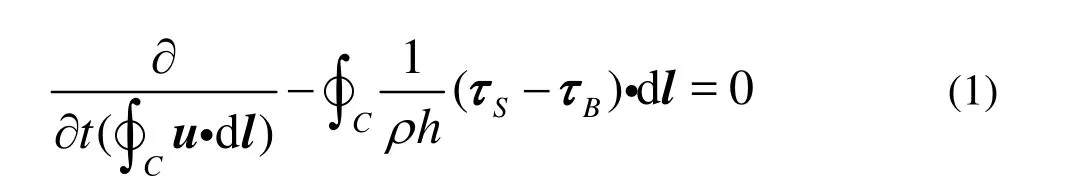
wherelis the island boundary line,tis the integral time,ρis the sea density,his the sea depth. The integration is along the island coast. This integral constraint is applied to flows and wave propagations around islands and through gaps[7,24]. Yang[7]studied it

in the static state. In our study,uvaries with time, unlike in previous studies. The monthly mean data used for the interannual variation of the NB, with time scale larger than the adjusted time of the current itself, such as in the topography rossby wave. So Eq.(1) is expressed as

whereSτis the surface pressure,Bτis the bottom pressure, which means that the integral friction around the island is zero. The pressure difference between the south and north tips balances the friction:

wherePAis the southeast pressure along the Japan Island set by the KC, andPBis the northeast pressure along the Japan Island set by the KC,τfrictionis the composition of forles between islandBτ. So the ocean in the other side of the Japan Island also experiences the same Δp, which tends to force a northward boundary flow, the NB. The KC experiences a low frequency variation with time, and its path and strength are also changed. The Δpforced by the KC should vary with the friction.

We calculate the current fields in annual mean from 1991 to 2000. The results show that the path of the KC along the southeast coast of Japan Island changes its direction during the running model years. We define the types of paths using the method of Qiu[20], that is, NLM and LM, respectively (see Fig.7). It is shown that the Δpforced by the KC along the southeast coast of Japan Island may change the NB against time.

In the next step, we calculate the pressure along the Japan Island from Point A to Point E in clockwise direction under two types of KC paths (see Fig.9(a)). The results show that the pressures at A and E are similarly higher, and push the flow northward. The values of Δptowards A-B-C-D are decreased, the pressure towards E-D are also decreased, with the

minimum being located around D. The Δpis larger under NLM pattern than under LM pattern (see Fig.9(b)). Comparison of the volume transports (See Fig.8) shows a good agreement between the KC and the NB. When the KC is robust in NLM pattern, the NB is strong. On the other hand, when KC is weak in LM pattern, the NB is decreased.

5. Conclusion

The KC’s axis and volume transport variations in the interannual time scale are simulated and analyzed in this article by using HYCOM. The model results show that the NB is affected by the northward flow, the KC along the east bank of Japan Island according to the island integral constraint. The KC exerts a strong friction in the anti-cyclonic direction along the eastern coast of Japan, so a cyclonic friction must exist along the other side, i.e., the western coast in the JES, must exist. This results in the NB. This we proposes as a hypothesis, which is used to study the KC’s interannual variability and its effect on the NB. The path of the KC in the southeast of Japan varies with time. So Δpis adjusted continuously to keep a balance with the friction. With the two type paths of the KC, the volume transports into the JES are different. When the KC is robust in NLM pattern, the NB is strong. On the other hand, when the KC is weak in LM pattern, the NB is decreased.

Fig.9 Several pressure points

Acknowledgment

The authors are grateful to Dr. Yang Jia-yan of the WHOI, USA, for his discussion. We would also like to express our thanks to anonymous reviewers for their constructive comments on the manuscript.

[1] ISOBE A. Two-layer model on the branching of the Kuroshio southwest of Kyushu[J].Journal of Physical Oceanography,2000, 30(9): 2461-2476.

[2] SPALL M. A. Wind- and buoyancy-forced upper ocean circulation in two-strait marginal seas with application to the Japan/East Sea[J].Journal of Geophysical Research,2002, 107(C1): 6-1-6-12.

[3] KIM K., CHANG K. I. and KANG D. J. et al. Review of recent findings on the water masses and circulation in the East Sea (Sea of Japan)[J].Journal of Oceanography,2008, 64(5): 721- 735.

[4] HOLLOWAY G., SOU T. and EBY M. Dynamics of circulation of the Japan Sea[J].Journal of Marine Research,1995, 53(4): 539- 569.

[5] ZHENG Pei-nan, WU De-xing and LIN Xiao-pei. Therelationship between the Taiwan Warm Current and Tsushima Warm Current[J].Journal of Hydrodynamics,2009, 21(2): 212-218.

[6] XU Ling-ling, WU De-xing and LIN Xiao-pei et al. The study of the Yellow Sea Warm Current and its seasonal variability[J].Journal of Hydrodynamics,2009, 21(2): 159-165.

[7] YANG J. Y. An oceanic current against the wind: How does Taiwan Island Steer Warm Water into the East China Sea?[J].Journal of Physical Oceanography,2007, 37(10): 2563-2569.

[8] HOU Yi-jun, SU Jing-zhi and FANG Guo-hong et al. The effect of Kuroshio on the circulation in China Seas from satellite-tracked drifter data[J].Journal of Hydrodynamics, Ser. B,2003, 15(4): 109-112.

[9] BAI Xue-zhi, BAI Hong and HU Dun-xin et al. Cyclonic recirculation on the left side of the Kuroshio in the East China Sea[J].Journal of Hydrodynamics, Ser. B,2001, 13(3): 133-137.

[10] XIA Chang-shui, QIAO Fang-li and ZHANG Qing-hua et al. Numerical modeling of the quasi-global ocean circulation based on POM[J].Journal of Hydrodynamics, Ser. B,2004, 16(5): 537-543.

[11] ERIC P., HURLBURT E. and MARTIN O. The HYCOM (Hybrid Coordinate Ocean Model) data assimilative system[J].Journal of Marine Systems,2007, 65(1): 60-83.

[12] ZHAO Wei, HOU Yi-jun and QI Peng et al. The effects of Monsoons and connectivity of South China Sea on the seasonal variations of water exchange in the Luson Strait[J].Journal of Hydrodynamics,2009, 21(2): 264-270.

[13] KISTLER R., KALNAY E. and COLLINS W. et al. The NCEP - NCAR 50 - year reanalysis. Monthly means CD - ROM and documentation[J].Bulletin of the American Meteorological Society,2001, 82(2): 247 -268.

[14] LARGE W. G., DANABASOGLU G. and DONEY S. C. et al. Sensitivity to surface forcing and boundary layer mixing in a global ocean model: Annual-mean climatology[J].Journal of Physical Oceanography,1997, 27(11): 2418-2447.

[15] TAKIKAWA T., YOON J. H. and CHO K. D. The Tsushima Warm Current through Tsushima Straits estimated from ferryboat ADCP data[J].Journal of Physical Oceanography,2005, 35(6): 1154-1168.

[16] DONG Chang-ming, ZHANG Qing-hua. On further application of the thin-jet model into the bimodality of Kuroshio[J].Chinese Journal of Oceanology and limnology,1995, 26(5): 566-569(in Chinese).

[17] DONG Chang-ming, ZHANG Qing-hua. Dynamic study on bimodality characteristic of Kuroshio[J].Acta Oceanologica Sinica,1995, 17(1): 130-136(in Chinese).

[18] DONG Chang-ming, CHEN Shui-ming and ZHANG Qing-hua et al. On multiple solutions to a low-spectrum model of oceanic current driven by the boundary force-the bimodality of the Kuroshio South of Japan[J].Chinese Journal of Oceanology and limnology,1996, 14(2): 113-120.

[19] KAWABE M. Variations of current path, velocity, and volume transport of the Kuroshio in relation with the large meander[J].Journal of Physical Oceanography,1995, 25(12): 3103-3117.

[20] QIU B., MIAO W. Kuroshio path variations South of Japan: Bimodality as a self-sustained internal oscillation[J].Journal of Physical Oceanography,2000, 30(8): 2124-2137.

[21] AKIHIKO M., YANAGI T. Variability of sea surface circulation in the Japan Sea[J].Journal of Oceanography,2001, 57(1): 1-13.

[22] YOUNG H. S. Significance of shallow bottom friction in the dynamics of the Tsushima Current[J].Journal of Oceanography,2003, 59(1): 113-118.

[23] CHO Y. K., KIM K. Branching mechanism of the Tsushima Current in the Korea Strait[J].Journal of Physical Oceanography,2000, 30(11): 2788-2797.

[24] PEDLOSKY J., PRATT L. and SPALL M. et al. Circulation around islands and ridges[J].Journal of Marine Research,1997, 55(6): 1199-1251.

November 4, 2009, Revised March 18, 2010)

* Project supported by the National Basic Research Program of China (973 Program, Grant Nos. 2005CB422302, 2005CB422303, 2007CB411804), the National Natural Science Foundation of China (Grant Nos. 40706006, 40930844), the key project of International Science and Technology Cooperation Program of China (Grant No. 2006DFB21250), the Ministry of Education’s 111 Project (Grant No. B07036), and the Program for New Century Excellent Talents in University (Grant No. NECT-07-0781).

Biography:ZHENG Pei-nan (1981- ), Male, Ph. D., Engineer

2010,22(3):305-311

10.1016/S1001-6058(09)60059-7