原子光谱项与分子的电子光谱项

黄正国徐梅芳

(1天津师范大学化学与生命科学学院 天津300387;2天津师范大学数学科学学院 天津300387)

知识介绍

原子光谱项与分子的电子光谱项

黄正国1徐梅芳2

(1天津师范大学化学与生命科学学院 天津300387;2天津师范大学数学科学学院 天津300387)

原子光谱项与分子的电子光谱项是结构化学中的重要概念之一。本文介绍了原子光谱项和分子的电子光谱项的由来，并分析了二者之间的区别和联系。

描述原子中单个电子的运动状态可以采用n、l、m、ms这4个量子数。原则上讲，无论是原子体系还是分子体系，其整体状态均取决于原子核外所有电子的运动状态。在每一个原子中，由主量子数n、角量子数l描述的原子中的电子排布方式称为组态［1］，例如基态碳原子的电子组态为1s22s22p2。电子组态也可以用于表示分子的电子排布，例如Li2的电子组态为(1σg)2(1σu)2(2σg)2。组态可以很好地表示单个电子的状态，但在多电子原子或分子体系中，由于电子之间存在着排斥作用，并且电子的轨道运动和自旋运动也存在相互作用，使原子或分子的整体状态并不等于各个单电子状态的简单相加，因此组态只是对原子或分子状态的一种粗略描述，不足以说明整个原子或分子的状态，不能采用组态来描述原子或分子的整体状态［2］。通常使用原子光谱项来描述原子的状态，使用分子的电子光谱项来描述分子的状态。这就涉及以下两个问题:①原子光谱项和分子的电子光谱项是如何得到的?②原子光谱项和分子的电子光谱项的区别和联系是什么?本文将针对这两个问题进行简要的分析介绍。

1 角动量耦合与原子光谱项

根据角动量守恒原理可知，在没有外界影响的情况下，一个微粒的运动或包含若干微粒运动的体系，其总角动量是保持不变的。原子内只有一个电子时，可粗略地认为它的轨道角动量和自旋角动量彼此独立，又都保持不变。但严格地说，这两个运动产生的磁矩之间有磁的相互作用，但总角动量始终保持恒定。

在多电子原子体系中，电子之间的相互作用是非常复杂的，大体可以分为以下3种:电子轨道运动之间的相互作用，电子自旋运动之间的相互作用以及轨道运动与自旋运动之间的相互作用。具体而言，在多电子原子体系中，由于电子之间存在静电排斥作用，各电子的轨道运动会相互影响，因此单个电子的轨道角动量Ml是不确定的，但所有电子的总轨道角动量ML保持不变;同样单个电子的自旋角动量Ms也是不确定的，而所有电子的总自旋角动量MS保持不变。严格地讲，总轨道角动量ML和总自旋角动量MS也会发生相互作用，但由二者耦合成的总角动量MJ保持不变。根据以上原理，Russel和Sauders提出了L-S耦合方案［3］:其中L为原子的角量子数，S为原子的自旋量子数，该方案适用于电子间的静电作用大于轨道－自旋耦合作用的原子(一般指Z＜40的原子)。除了L-S耦合方案外，还有一种j-j耦合方案，适用于轨道－自旋耦合作用大于电子间静电作用的原子(一般指Z≥40的原子)。

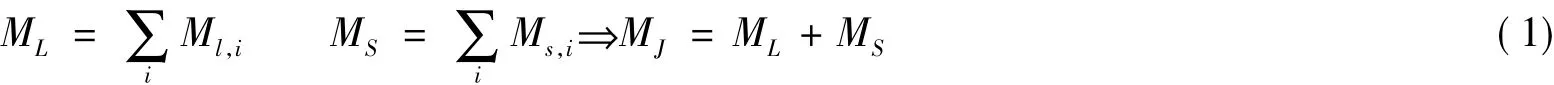
根据以上分析可知，原子的运动状态可以用电子的总轨道运动和总自旋运动来表示。对原子的同一组态而言，若不计轨道－自旋相互作用，且在没有外界磁场作用下，L和S都相同而ML和MS不都相同的诸状态，都具有完全相同的能量。因此，将同一组态中由同一个L和同一个S构成的诸状态合称为一个光谱项:

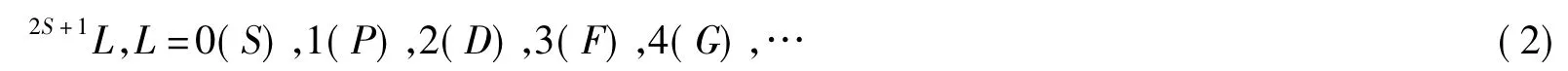
(2S+1)称为自旋多重度。每一个光谱项相当于一个能级。如果考虑到轨道－自旋相互作用，则电子的总轨道角动量ML和总自旋角动量MS都不再守恒，而由二者耦合而来的总角动量MJ仍是守恒的，所以描述原子状态时需要进一步考虑原子的总量子数J，即用光谱支项2S+1LJ描述原子状态。当外磁场存在时，每一个光谱支项2S+1LJ又可分裂为(2J+1)个微观能态。

由于内层轨道已全填充满，L=0，S=0，所以推导原子基态光谱项时可只考虑该原子的价层电子排布。表1列出了原子的价层轨道全充满、半充满以及半充满以前的各电子组态的基态光谱项。此外，由于Pauli原理的限制，等价电子组态存在“电子－空位”关系，即n个电子的某一组态的光谱项与n个空位的光谱项相同，又称作互补定理。所以根据表1也可以方便地推导出半充满以后的各电子组态的基态光谱项。

表1 原子的基态光谱项

2 线性分子的电子光谱项

如果不考虑轨道－自旋相互作用，则电子的总轨道角动量ML和总自旋角动量MS都是守恒的。对于线性分子，轨道角动量已经不再守恒，但由于线性分子还保留有键轴(通常为z轴)对称性，所以轨道角动量只有在键轴方向才是守恒的。所以，线性分子中单个电子的轨道角动量的z轴方向分量是量子化的，其值为mħ(m=0，±1，±2，…)。由于电子运动的方向正转和反转能量相同，以λ=|m|(0，1，2，…)将轨道分别记为σ，π，δ等轨道，其中λ为分子轨道角动量轴向分量量子数，所以分子轨道能量只与λ有关。

对于线性分子，根据角动量的耦合规则，分子总轨道角动量在z轴方向分量Mħ为各单电子轨道角动量的z方向分量mħ的代数和:

M的绝对值通常用大写Λ表示:

Λ为分子总轨道角动量在z方向的分量量子数。Λ不同，线性分子能量也不同，并且Λ≠0的状态是双重简并的。

在线性分子中，如果不考虑旋－轨耦合，则分子的总自旋角动量仍可认为是守恒的，所以线性分子的总自旋角动量为:

S为总自旋量子数，(2S+1)为分子的自旋多重度。所以线性分子的电子光谱项为:

线性分子如有对称中心，则用g或u表示中心对称性，记做2S+1Λg或2S+1Λu。同原子光谱项类似，双原子分子的光谱支项为:

如果分子有对称中心，分子谱项右下角也会有宇称符号g与u。此外，对于Σ谱项(Λ=0)，右上角若有+、－号，则代表其对包含键轴的平面的对称性。

对于线性分子的电子光谱项，可根据该分子的最高占据轨道(HOMO)的电子排布来定。线性分子的基态光谱项见表2。同原子体系一样，在分子中也存在互补定理，即开壳层组态(λ)p与它的互补组态(λ)p－1(p为该壳层容纳的最大电子数)具有相同的谱项。

表2 线性分子的基态光谱项

3 非线性分子的电子光谱项

对于原子的状态，可以用由原子量子数L和S构成的原子光谱项2S+1L表示;对于线性分子的电子态，可以用由量子数Λ和S构成的电子光谱项2S+1Λ表示;而对于非线性分子，由于没有轴向对称性，所以不能用一个量子数来表记电子态。又由于体系的哈密顿算符和转动算符对易，二者具有相同的本征函数，从而体系波函数可作为不可约表示的基，所以非线性分子的轨道及电子状态都可用分子所属点群的不可约表示来描述。例如，H2O属于C2v点群，电子排布为(a1)2(a1)2(b2)2(a1)2(b1)2，其中a1，a2，b1，b2表示分子轨道。非线性分子体系的对称性即为所有电子占据轨道的直积，由于H2O分子中所有内层轨道都是全充满的，所以只需考虑HOMO即可获得H2O体系的对称性:

如果表示分子的电子状态，则是在对称性的左上角给出分子的自旋多重度(2S+1)，所以H2O的电子光谱项为1A1。

所以，通常采用分子所属点群的不可约表示来表示非线性分子的电子光谱项:

其中Γ为分子所属点群的不可约表示，不可约表示符号的意义如下［4］:

①一维表示标记为A或B，用E、T、U和W分别标记二、三、四、五维不可约表示。

③如果有对称中心，则用“u”或“g”标记反演是对称或反对称的。

④如果有水平镜面σh，则用“'”或“″”表示对于σh的反映为对称或反对称的。

⑤如果上述标记还不足以区分全部表示时，再加上下标1，2，…。对于一维表示A或B，下标1和2分别标记对垂直于主轴的C2轴是对称的或反对称的;如果没有C2轴，则标记对垂直镜面的反映是对称的或是反对称的。对于二维表示，下标1和2标记绕主轴Cn转动角度中p的n数值。对于三维表示T，下标1和2只是用于识别，例如T1和T2是两个不同的三维不可约表示。

非线性分子的电子光谱项是由该分子的最高占据轨道(HOMO)的电子排布来确定的。HOMO为全充满时，只有一种状态1ΓTS(全对称表示);HOMO只有1个电子，即(Γi)1，则电子光谱项为2Γi;HOMO有2个单电子，即(Γi)1(Γj)1，则(Γi)⊗(Γj)=Γij，所以电子光谱项为1Γij和3Γij。例如，乙烯分子具有D2h对称性，它的某一激发态电子组态为:

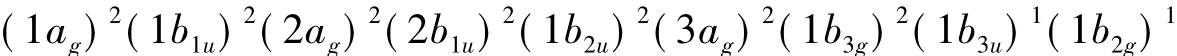
则B3u⊗B2g=B1u，取自旋多重度3，故相应的分子谱项为3B1u。

4 原子光谱项与分子的电子光谱项的关系

原子光谱项与分子的电子光谱项并没有严格的区别，其本质都是电子光谱，都是用电子的运动状态来表示体系的状态，但意义有所不同。对于多电子原子，由于轨道－自旋相互作用，单电子的轨道角动量和自旋角动量不再守恒，只有体系的电子总轨道角动量和总自旋量子数守恒(不考虑轨道－自旋相互作用以及磁场的作用)，因此可以用原子角量子数L和原子自旋量子数S表示原子的状态;对于线性分子，轨道角动量也已经不守恒，但还具有轴向对称性，因此轨道角动量在z轴方向上的分量是守恒的，因此用此分量来表示线性分子的状态;对于非线性的分子，角动量已失去意义，因此用单电子轨道的对称性的直积来标志体系的状态。其实，用于表示线性分子状态的Σ、Π、Δ等符号也是相应分子点群的不可约表示符号，因此，可以简单地认为，原子光谱项是用原子量子数表示的，而分子的电子光谱项则是用由其所属点群的对称性来表示。对于体系的电子多重度，无论是原子体系还是分子体系，均为2S+1。原子光谱项与电子光谱项的对应关系见表3。

此外，无论是原子光谱项还是分子的电子光谱项，谱项标记与轨道标记都是有联系的。原子光谱项是用原子量子数标记的，原子轨道的标记则相应地由电子量子数来标记。例如，碳原子的电子排布为(1s)2(2s)2(2p)2，原子光谱项为2P。分子的电子光谱项是用由其所属点群的不可约表示来标记的，分子轨道的标记也是其所属点群的不可约表示来标记的。例如H2O的电子排布为(a1)2(a1)2(b2)2(a1)2(b1)2，电子光谱项为1A1。表3也给出了谱项标记与轨道标记之间的对应关系。

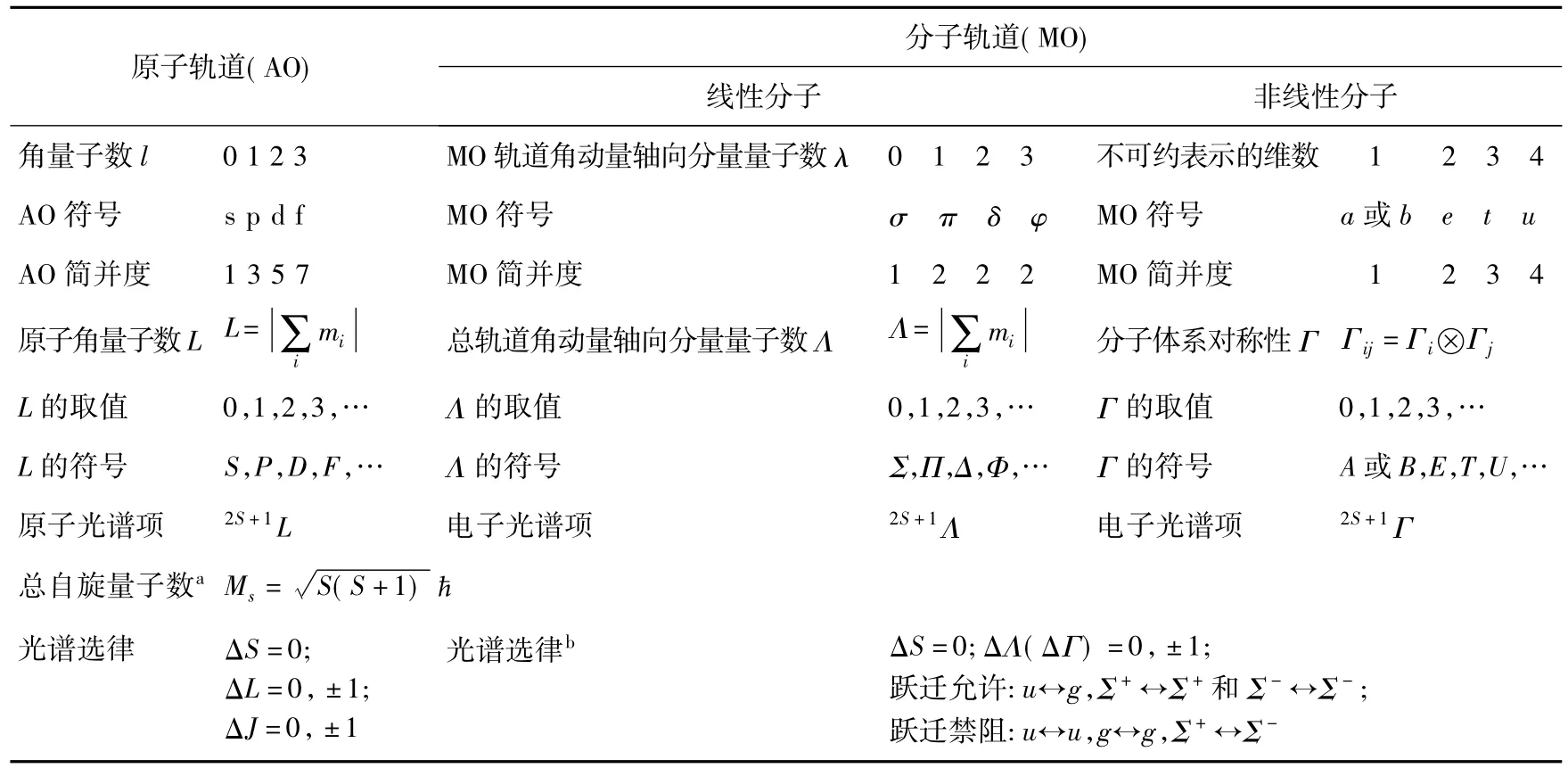
表3 原子的基态光谱项原子光谱项与电子光谱项的比较

5 光谱选律

原子光谱和电子光谱一样，都是电子在不同原子或分子能级之间的跃迁产生的。一个原子光谱项或电子光谱项都代表一个能级，不同之处在于，前者会分裂为多个光谱支项，在光谱上表现为原子光谱的精细结构;而后者往往会伴随有振动和转动光谱，在光谱上表现为电子光谱的精细结构。

在光谱学中，ψi→ψj电子跃迁的强度依赖于电荷跃迁偶极矩矢量μ，相应的矩阵元μij为:

如果ψi，μ，ψj对应的不可约表示的直积包括全对称的不可约表示，则矩阵元μij不为0，这就是光谱选律［5］。所以并不是电子在任意两个能级之间都可以发生跃迁，电子跃迁必须满足一定的条件。

5.1 原子光谱选律

对于L-S耦合模型，原子光谱选律为:

①ΔS=0;ΔL=0，±1;ΔJ=0，±1;

②ΔL=0，±1(但从L=0到L'=0禁阻);

③ΔJ=0，±1(但从J=0到J'=0禁阻);

④ΔMJ=0，±1(但ΔJ=0时，从MJ=0到MJ'=0禁阻)。

只有遵循原子光谱选律的跃迁才是允许的跃迁，其余跃迁不能发生或几率很低，谱线较弱。另外，这些选律在轨道－自旋耦合作用变强时(例如重原子中)会逐渐失效，在j-j耦合方案中完全不起作用。

5.2 双原子分子的电子光谱选律

同原子光谱一样，并不是电子在任意两个能级之间的跃迁都可以产生电子光谱，双原子分子电子光谱的产生也必须满足一定的光谱选律:

①ΔS=0;ΔΛ=0，±1;

② 对Σ态，Σ+↔Σ+和Σ－↔Σ－跃迁允许，而Σ+↔Σ－跃迁禁阻;

③对同核双原子分子，g↔u跃迁允许，而g↔g和u↔u跃迁禁阻。可见，原子光谱选律与双原子分子的电子光谱选律有类似之处:

不同之处在于，对于原子，原子角量子数L仍是有意义的，所以可以用L来表示光谱选律;而对于分子，由于轨道角动量已失去意义，因此改由分子总轨道角动量在z方向的分量量子数Λ来表示光谱选律。

6 结论

原子光谱项与分子的电子光谱项在实质上是一样的，都代表某个能级。电子在原子能级或分子能级之间的跃迁所表现出的原子光谱或电子光谱可以分别用原子光谱项或分子的电子光谱项来表示;从原子光谱项或电子光谱项中也可以获得光谱选律的有关信息。总之，光谱项是一个非常重要的概念，在进行光谱分析时有重要用途，因此正确认识原子光谱项与分子的电子光谱项，以及二者之间的区别和联系是很有必要的。

［1］ 周公度，段连运.结构化学基础.第3版.北京:北京大学出版社，2002

［2］ 潘道皑，赵成大，郑载兴.物质结构.第2版.北京:高等教育出版社，1989

［3］ 林梦海.量子化学简明教程.北京:化学工业出版社，2005

［4］ 高松，陈志达，黎乐民.分子对称性群.北京:北京大学出版社，1996

［5］ 麦松威，周公度，李伟基.高等无机结构化学.第2版.北京:北京大学出版社，2006