非最小相位系统的自适应逆控制

杨巧德，张侃健

（东南大学自动化学院, 南京 210096）

1 引言

动态系统的逆模型问题一直是工业控制策略中重要的组成部分。逆模型的精确程度在一定程度上影响了整个控制系统的性能，尤其对于高性能运动控制，其前向控制器的补偿很大程度上依赖于逆模型的结构。

对于最小相位系统，其逆是稳定的因果的，而非最小相位系统因不稳定零点的存在，使得系统存在两种逆，一为因果的但不稳定，二为稳定但非因果，这在实际中是无法实现的。很多文献对该系统的逆模型进行了讨论，文献[1]针对SISO对象的逆模型提出了各种不同的控制算法，包括精确的和近似的逆模型算法，其中零相位误差跟踪控制（ZPETC）得到了大量的应用。文献[2]将非最小相位系统的逆问题转化为了H∞范数优化的最优模型匹配问题，这类问题的求解大部分要借助于Nevanlinna-Pick插值或者迭代方法。文献[3]借助于神经网络来直接或间接地辨识模型的逆。文献[4]结合Widrow和Walach提出的自适应逆控制的方法，将神经网络用于模型的辨识和逆控制。但是这些方法适合于离线的学习，当模型结构具有不确定性或模型不匹配时，实际系统的调节时间要比仿真的结果差，因此，在线学习则需要相应地改变。

与最小相位系统相比，非最小相位系统的一个最大特征就是阶跃响应呈现负调或反向响应特性。该负调是无法避免的，而且在某些系统中是十分不利的，必须对过大的负调加以限制[5]，许多文献恰恰忽视了这方面的限制[6]。消除负调最理想的方法就是零极点对消，但在实际中是不可行的，因为这会使得控制器中含有不稳定的极点，从而使得级联的系统具有无界的内部信号，这实际上使整个的系统隐藏了不稳定部分[7]。虽然非最小相位系统的逆不易获得，但可以用近似的逆来代替，特别是自适应逆控制、神经网络的发展，使得控制实现更加容易。

针对非最小相位系统逆的问题，本文采用N拍带延迟的FIR滤波器结构近似逆系统，使得逆控制器本身是稳定的，又避免了直接的零极点对消。逆建模时，首先根据对象的先验知识离线训练对象的逆模型，然后作为一个前向控制器，再通过LMS算法在线调节控制器中的参数。离线阶段，通过RLS滤波算法最小化模型输出误差，得到对象的近似逆模型；在线阶段，通过LMS算法反传对象的误差信号最小化系统的输出误差。仿真发现，自适应逆控制既克服非最小相位的负调现象，又使得系统具有较快的响应速度。

2 自适应逆控制结构及算法

2.1 自适应逆控制

自适应逆控制是一种基于动态逆概念的设计方法，其基本的思想就是把对象动态特性看成映射，控制器逼近逆映射，使对象的输出跟随指令输入[8]。它本质上属于开环控制，利用对象特性的逆作为控制器，与被控对象串联。与传统的控制系统相比，自适应逆控制最大的优点在于被控对象动态响应和消除扰动控制可以单独设计，互不影响，一种控制的最优不会牺牲另一种控制的最优。

完整的自适应逆控制包括被控对象的辨识、逆控制器、扰动消除器三部分。对于自适应逆控制来说，它本质上是属于开环系统，必须对扰动加以抑制，否则扰动会毫无保留地出现在输出端。与常规的扰动消除不同，常规的扰动消除只需要从外部获取其参考信号，用此信号按前馈滤波来实现扰动消除；自适应逆控制中的对象输出扰动消除则要从对象输出中获得相应的扰动参考信号，再用此信号按反馈滤波并从对象输入中减去来实现。

2.2 自适应逆控制系统

对于一个连续时间的未知对象，设传递函数为P( s)，经离散化后得到系统的离散模型为：

系统跟踪的误差为：

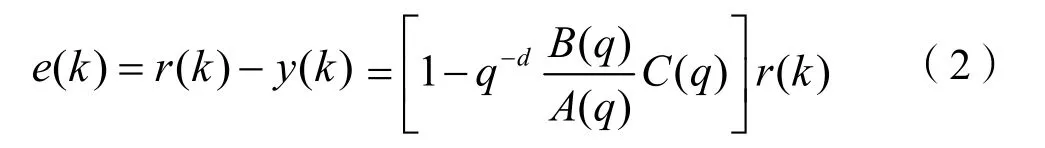
根据Parserval定理可知：

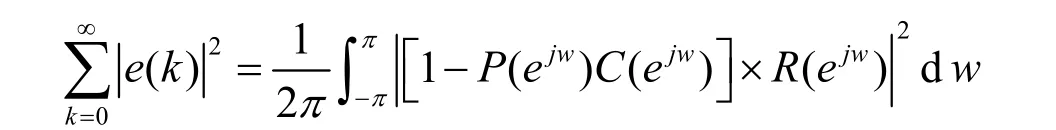
即

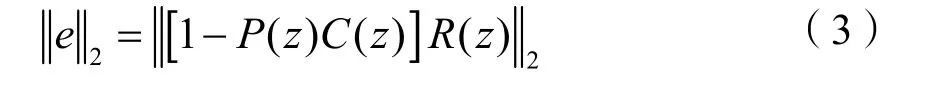
整个控制系统的目标就是使得误差逼近于0，对于最小相位系统， C ( z)= 1 P( z)，满足该准则。但对于非最小相位系统，由于零点位于单位圆外，使得系统的逆是不存在的。但是我们通过近似的逆来逼近非最小相位系统中不可逆的部分，目前，常借助于零相位跟踪误差控制（ZPETC）、神经网络、IIR或FIR滤波器方法，而DSP中滤波器设计方法相对成熟，实现更加方便。FIR滤波器只需要选择合适的参数和滤波器的阶数就可以使得输出误差最小化。本文模型辨识、逆建模过程均采用自适应FIR滤波器的设计方法。

2.3 对象的正建模

正模型是逆模型的前提，逆模型辨识的好坏取决于正模型辨识的结果。对于具有先验知识的系统，为了利用有限的观测值来估计未知的参数，采用递推加权最小二乘算法。

由（1）式可知系统的输出为

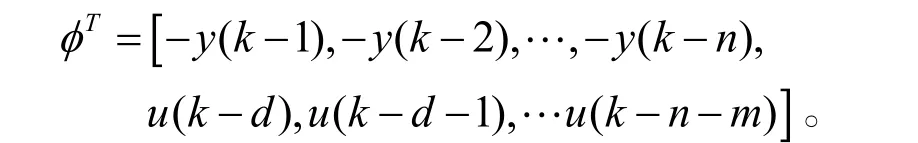
向量θ代表对象未知的参数，向量φ是由滤波器的输入输出信号构成的。递归加权最小二乘算法(RWLS）算法如下：

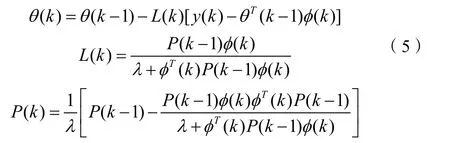
2.4 逆建模

逆模型的建立是以正模型为基础，图1为对象的离线情况下逆建模结构图，其中包括稳定对象和不稳定对象的情况。

自适应逆控制的前提是要保证系统是稳定的，否则，必须采用传统的反馈控制方法来镇定系统，控制结构如图1a所示。只有满足稳定的条件，才能保证自适应算法在不同的环境下是平稳收敛的。

对于非最小相位系统而言，对象的逆是不稳定的或非因果的。依据Shannon-Bode法，采用FIR滤波器构造近似逆模型是容易实现的，但有时候均方差误差会很大，若在控制系统中加入适当的延迟环节，可以降低最小均方误差。本文采用递推最小二乘的算法构造FIR滤波器实现非最小相位系统最优的延迟逆模型。

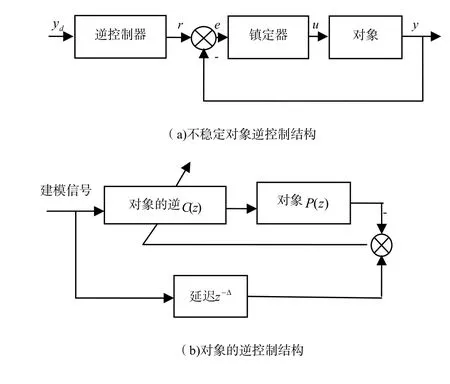
图1

3 对象逆模型的在线调整

离线建模时，逆模型对正模型的误差非常敏感，使得逆控制的效果有限。而在线调整可以解决两个问题：（1）单纯的FIR可能造成大的跟踪误差，（2）当系统随时间改变时，FIR滤波器的性能会降低[9]。为了提高收敛速度和获得好的动态性能，可采用LMS算法，以离线建模所得滤波器权值作为在线求逆控制器的初值，或者把LMS的输出作为控制量输入的一部分，最终可获得较为精确的逆模型，如图2所示。

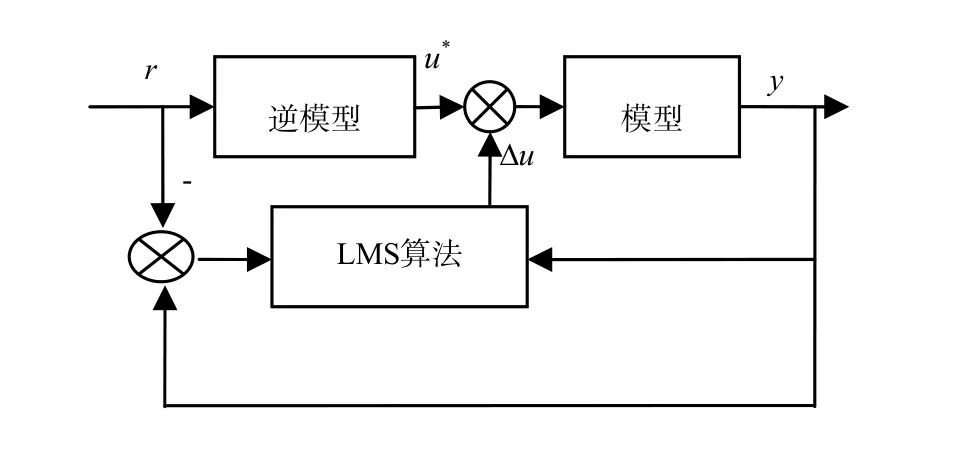
图2 逆模型的在线调整

下面给出在线调整算法可行性的证明。

对于SISO系统y=Pu

输出完全跟踪输出时，存在最优的*w使得，

令α=Pr，离散化后得到：

最小均方(LMS)算法是一种随机梯度算法，满足了在线更新的要求。它每次迭代时权矢量沿误差性能曲面的梯度估值的负方向更新，不需要计算有关的相关函数、矩阵求逆。简单易用，已在自适应滤波、自适应逆控制中得到了非常广泛的应用。

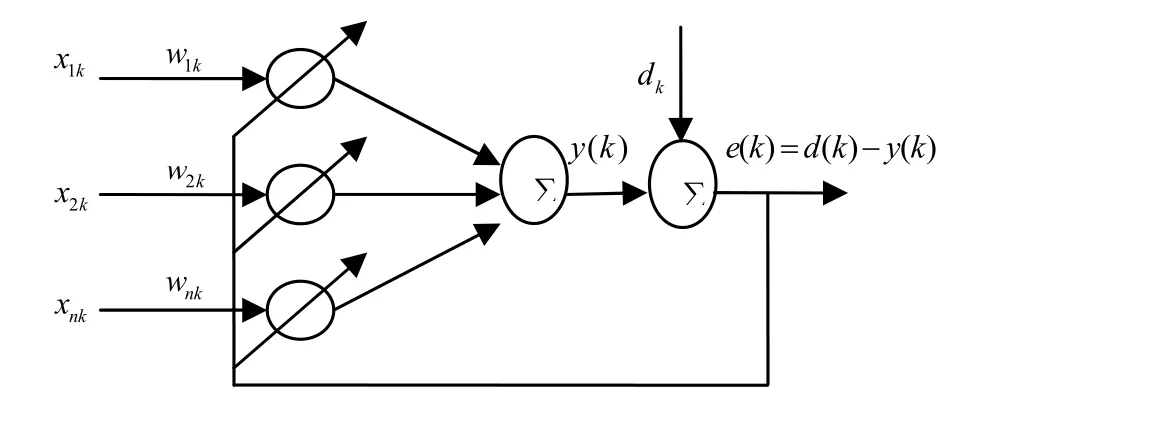
图3 自适应线性组合器

4 仿真实例

水轮发电机组系统是典型的非最小相位系统之一，该对象一直是控制中常用的控制模型[10]。该系统主要包括引水系统、水轮机、执行机构、电网（负荷）等几部分，图4为水轮机控制系统图，Mt是水轮机力矩，Qt为流量，H为水头，而水轮机的模型为：

图4 水轮机控制系统

考虑压力引水系统、发电机、负载及电液随动系统的动态特性，将系统进行线性化处理，得到如图5所示的线性化方框图，将图5化简得到系统的数学模型为（mg= 0 ）:

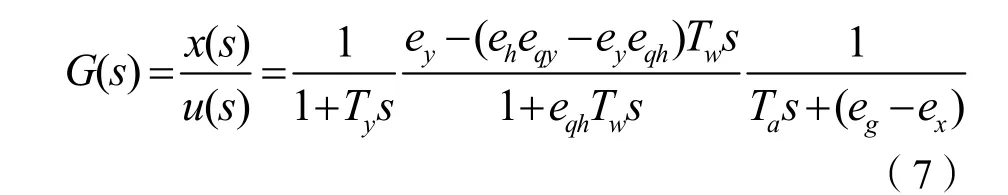
水轮机系统在某一实际工况下的参数[10]为：

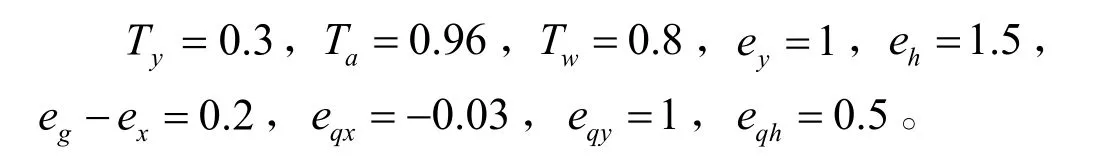
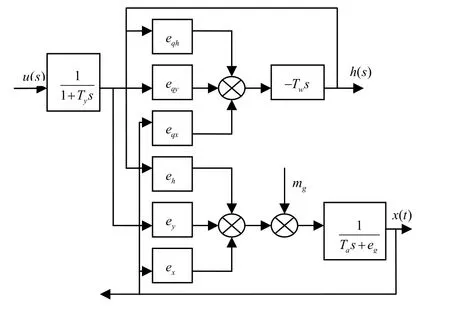
图5 水轮机线性化控制方块图

FIR滤波器采用128抽头的结构，系统的离散时间取为0.01s，采用白噪声作为输入，对象辨识的仿真结果如图6所示。

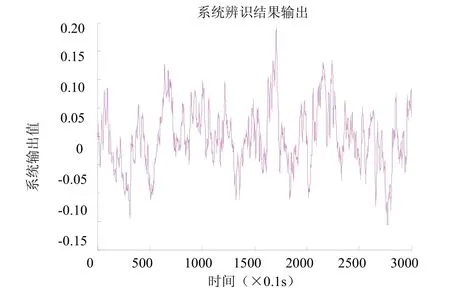
图6 对象辨识结果

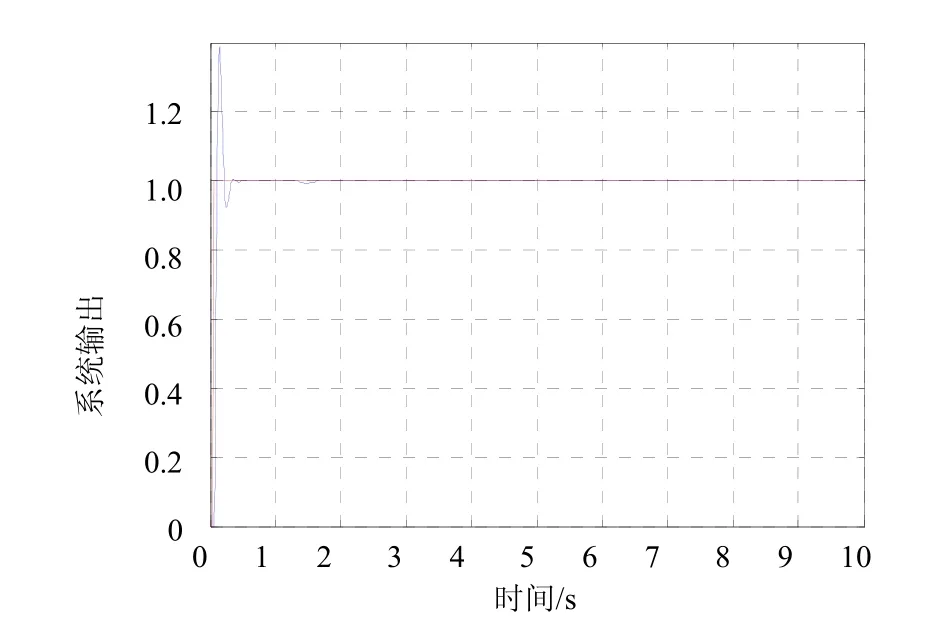
图7 自适应逆控制仿真

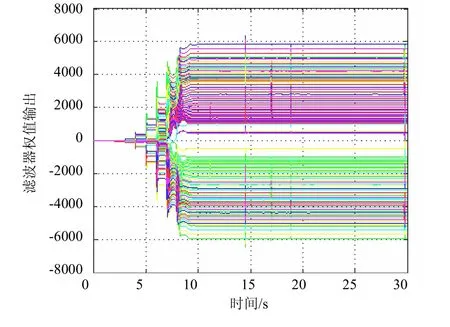
图8 逆模型中估计权值的输出

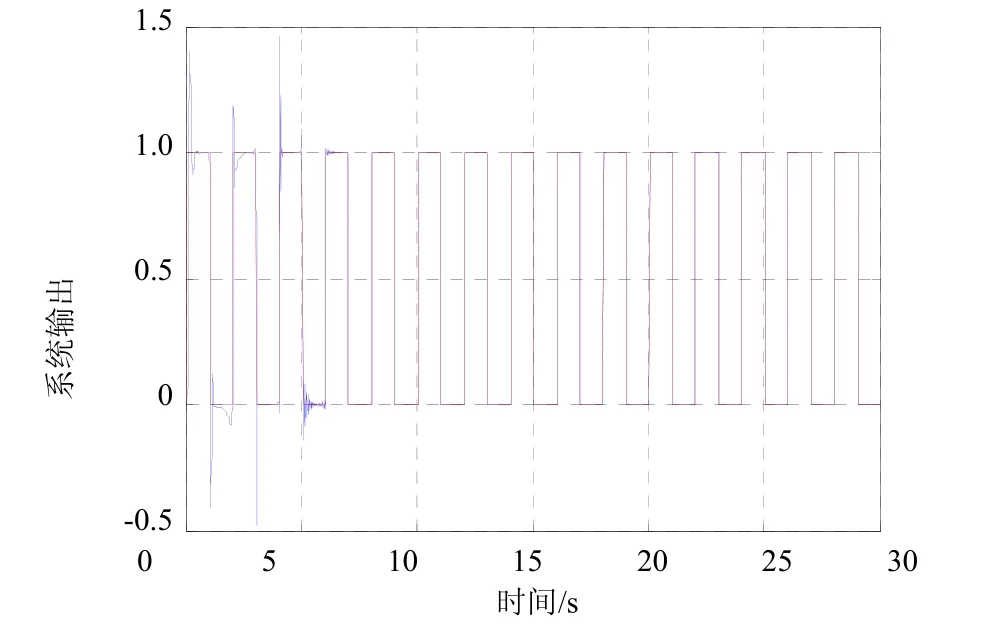
图9 输入信号为方波时系统的输出

图7是系统在阶跃信号下的输出结果，图8则为系统逆建模过程中RLS滤波器的估计权值。图9为系统在跟踪方波信号的输出图形。可以看出，系统能在很短时间内快速地跟踪输入信号，有较好的动态性能。

5 结论

本文针对非最小相位系统的特点，采用了自适应逆控制的方法，先通过FIR滤波器离线构造系统近似逆模型，再结合自适应LMS算法实施在线调整，而在线调整算法的加入使系统具备了一定的自适应和鲁棒性。仿真发现，该方法不仅解决了非最小相位系统的负调与调节时间耦合的问题，而且还使系统具有较好的动态性能。

[1][1]Brian P. Rigney. Adaptive Seettle-Optimal Control of Servomechanisms[D], 2008.

[2]吴旭东, 钟宜生, 解学书. 非最小相位不稳定对象的鲁棒最优模型匹配[J]. 自动化学报，1999, 25 (2):162-168.

[3]K. Lau, H. Middleton, and H. Braslavsky.Undershoot and Settling Time Tradeoffs for Non-minimum Phase Systems[J]. IEEE Transaction On Automatic Control, Vol.48, No.8, Augst 2003.

[4]Gregory L. Plett. Adaptive Inverse Control of Linear and Nonlinear Systems Using Dynamic Neural Networks[J]. IEEE Transaction On Neural Networks,Vol.14, No.2, March 2003.

[5]Ferry Hadary, Yasuhiro Ohyama, Shinji Hara.Undershoot Reduction for Plants with Real Unstable Zeros[C]. SICE Annual Conference in Fukui, Augst 4-6, 2003.

[6]M. Hanmandlu, Himani Goyal. Proposing a new advanced control technique for micro hydro power plants[J]. Electrical Power and Energy Systems, 2008,(30): 272-282.

[7]Nonminimum-phase Zeros[J]. IEEE Control Systems Machine.

[8]WIDROW B, WALACH E. 自适应逆控制[M]. 刘树棠，韩崇昭，译. 西安交通大学出版社，2000.

[9]John T. Wen and Ben Potsaid. An Experimental Study of a High Performance Motion Control System[C]. Proceeding of the 2004 American Control Conference Boston, 2004, 5158-5163.

[10]Variable Structure Neuron Control for Hydraulic Turbine Generators[C], Proceedings of the First International Conference on machine Learning and Cybernetics, Beijing, 2002, 1550-1553.