基于二代小波变换的电机转子不平衡故障检测

范炳奎，李颖晖，柳艳丽

（空军工程大学 工程学院，西安 710038）

1 引言

1996年，Sweldens和Daubechies提出了提升算法这种新的小波构造方案，被称为二代小波[1]。与传统小波从频域来分析问题的角度不同，二代小波变换完全在时(空)域进行变换，不依赖Fourier变换，小波基函数不再是由某一个函数的平移和伸缩而产生，所有的运算都在时域上进行，不仅能获得与传统小波变换同样的结果，而且实现信号在不同频带上的分离[2]，具有结构简单、运算量小、运算速度快、原位运算、不需要额外内存、可实现整数小波变换、逆变换可以直接反转实现等特点。

电机工作过程中，当电机产生电磁故障、电机转子不平衡、轴承不对中或轴承损坏等故障时，会产生不同的振动信号，引发不同的噪声[3]。通过分析这些振动信息，可以进一步了解和掌握电机的运行状态及电机的健康状况。传统的小波分析方法，由于小波基函数与各个尺度逼近信号的局部特征不能很好地匹配，当阈值选择不恰当时，滤噪效果不佳[4]。尤其当故障发生的初期，故障振动信号比较微弱，传统的小波分析方法就表现不佳。本文拟采用二代小波对电机振动信号进行变换分析，采用改良的软硬折衷阈值处理方法对小波系数进行量化处理，重构振动信号，分析重构信号，提取故障特征。研究表明:将第二代小波变换应用到电机突发性转子不平衡故障检测中，能够快速准确地提取其故障特征，提高了检测的准确性和可信度。

2 二代小波变换原理

第二代小波变换是由Sweldens提出的一种使用提升模式构造小波的方法。提升过程由分裂、预测、更新三部分组成[5]。

（1）分裂

分裂就是把信号分裂成两个相互关联的部分，通常根据信号的奇偶性将信号si分解为两个较小的子集偶数序列 si−1和奇数序列 di−1， di−1也称为小波集。设信号为si

（2）预测

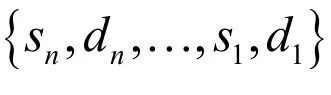
（3）更新

逆变换即重构的过程是分解的逆过程，包括反更新，反预测和合并。

（1）反更新

给定si−1和di−1，可以通过下式恢复偶数序列：

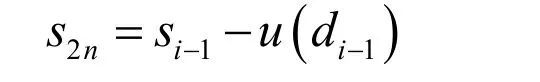
（2）反预测

由反更新得到的偶数序列s2n和给定的奇数序列可以反预测出奇数序列：

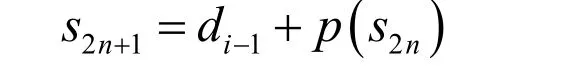
（3）合并

合并反更新的偶数序列s2n和反预测得到奇数序列s2n+1就可以恢复原信号：

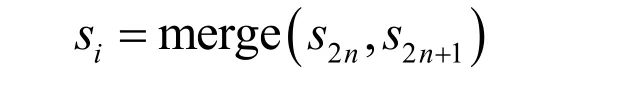
3 基于二代小波变换的电机突发性转子不平衡故障检测的原理

电机在工作过程中会发生不同程度的振动。当电机转子不平衡、滚动轴承异常、滑动轴承异常及安装、调整不良等都会引起机械振动。当电机转子质量分布不均匀时，会产生重心位移，引起变化的支撑力，导致电机运行不稳定，从而产生振动。电机转子不平衡根据现场发生的不平衡特征可以分为三类：（1）短时间停机后产生的不平衡；（2）长时间停机产生的不平衡；（3）运行中突然产生的不平衡。引起转子突发性失衡原因主要有: 动静碰磨；转子零部件脱落或移位；绝缘收缩造成转子线圈移位、松动；联轴器不平衡，负序电流过大引起套箍失去紧力；以及冷却风扇与转子表面均匀积垢等。转子突然失去平衡时的振动频率与转速频率相等，振动幅度随转速增高而加大[6]。对于每种类型和规格的电机，在稳定运行时，其振动都具有某种特定的典型特性。当电机转子出现突发性不平衡时，其振动的振幅、形式和频谱都会发生变化。基于第二代小波变换的转子突发性不平衡故障检测步骤如下：

（1）对振动信号进行二代小波变换，将振动信号分解为新的近似尺度系数si−1和小波系数di−1。

（2）对小波系数进行阈值处理，采用改良的软硬折衷阈值处理方法[7]，公式如下：

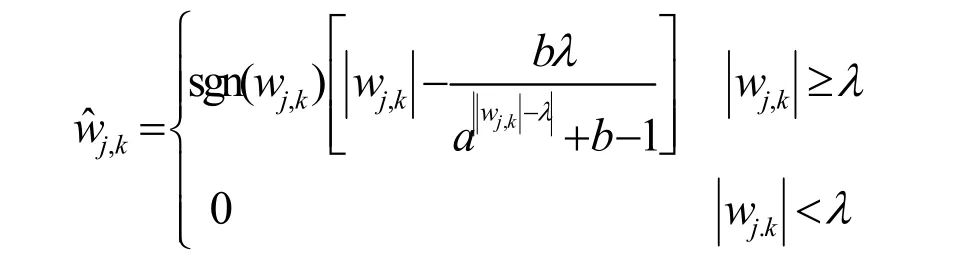
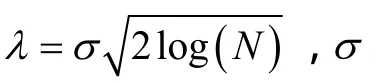
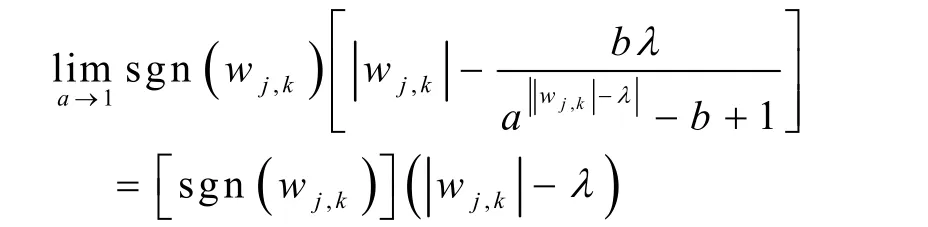
当a→+∞时，表现为硬阈值函数：

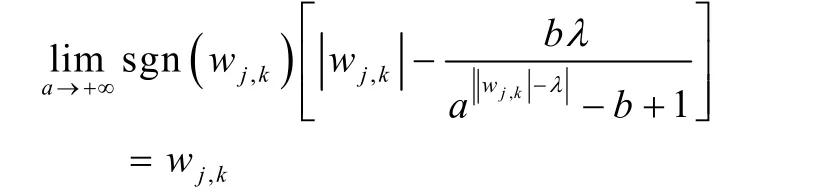
（3）对小波系数 di−1和尺度系数 si−1进行重构，结合转子突发不平衡时电机振动的特征，分析重构信号得出诊断结果。当重构的信号的振动频率特性和电机的转速频率基本相同时，就可以判断电机的转子发生了不平衡故障。

4 仿真试验

三相异步电动机Y315L-2额定电压Vn=380V，额定电流 In=365A，额定功率 Pn=200kW，额定转速ωn=2980r/min，振动为 4.5mm/s，噪声是 99dB。振动信号如图1所示。由于信号附有各种噪声信号，所以从图1中很难看出信号中包含周期成分，更不能确定周期成分的周期。其信号功率密度谱如图2所示。

先用传统小波变换对振动信号进行了分析，本文用“sym3”小波对信号进行3层分解并用软阈值对小波系数进行量化处理，采样频率= 1 000Hz ，重构信号的功率密度谱如图3所示。

由图 3可以看出，经传统小波消噪后的信号高频噪声基本被滤除，故障信号的频率也比较突出，但低频段消噪效果不理想，干扰故障诊断。尤其在故障发生初期，故障信号相对微弱，传统的小波分析就难以奏效。为了有效提取微弱信号，试采用第二代小波变换对振动信号进行分解，采样频率fs=1000Hz，对振动信号进行四层分解，取a=2000，b=13，对小波系数进行改良软硬折衷阈值处理，重构尺度系数和小波系数[9]，重构的信号如图4所示，其功率密度谱如图5所示。

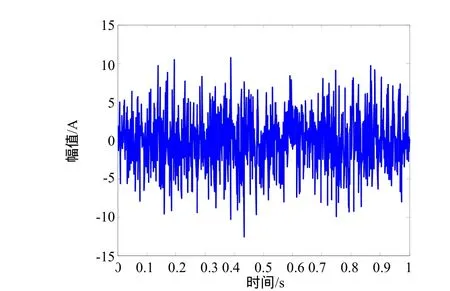
图1 振动信号波形

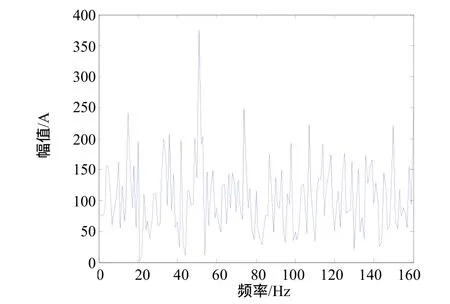
图2 振动信号功率密度谱图

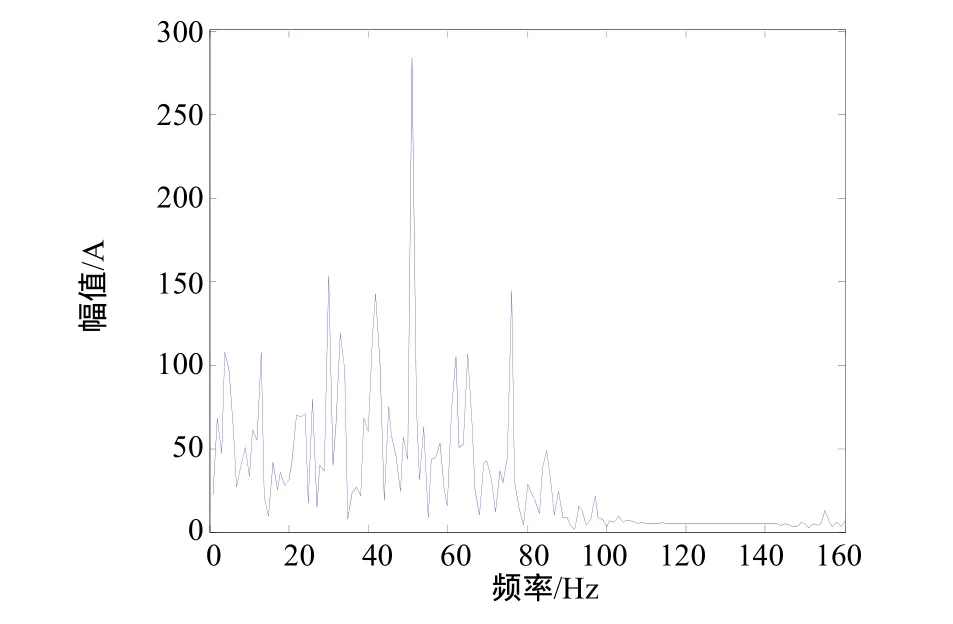
图3 传统小波方法重构信号的功率密度谱

由图5可以知道，第二代小波分析相对于传统小波分析，其消噪后的信号的故障信号频率更突出，低频段消噪效果也比较好，同时滤除了大部分的随机噪声，更能准确地提取故障信号的特征，提高了故障信号检测的可信度。由分析得出的故障信号的频率大约为 50Hz，电机的转速频率为 2980/60=49.7（Hz），参照电机故障特征，可以诊断出电机发生了转子不平衡故障。

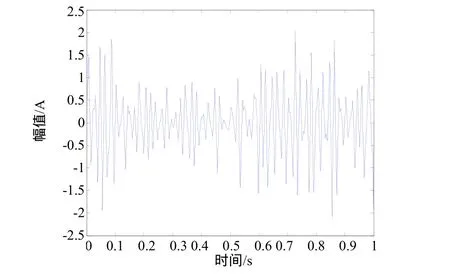
图4 二代小波方法重构的信号波形

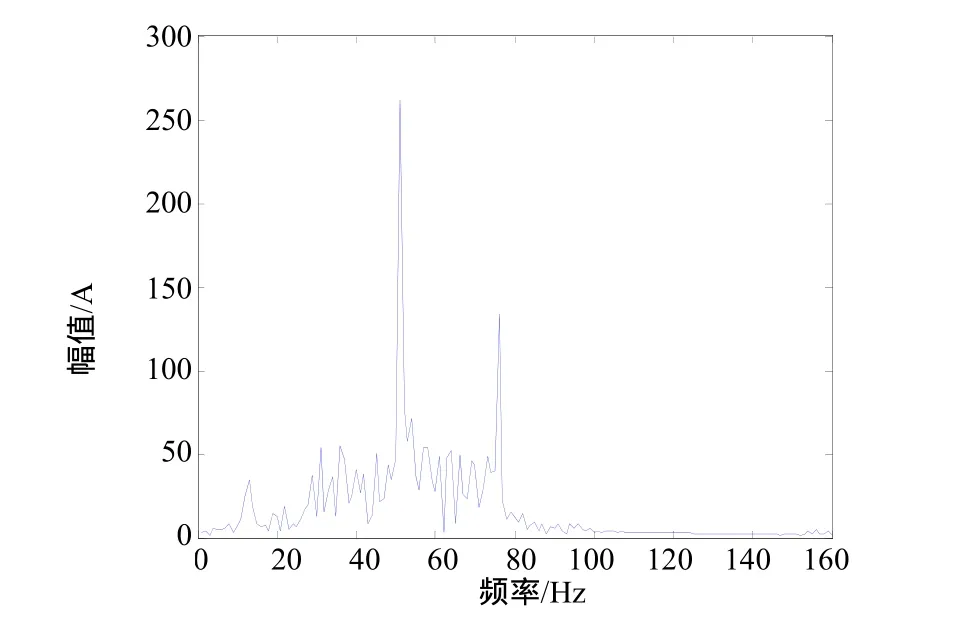
图5 二代小波方法重构信号的功率密度谱

5 结语

本文基于电机转子不平衡故障振动信号的特点，提出了用二代小波变换检测电机转子不平衡故障的方法。该方法克服了传统小波变换小波基函数与各个尺度逼近信号的局部特征不能很好地匹配和软阈值选择困难的局限性，能够去除大部分随机噪声并准确地提取故障信号特征，尤其是在故障振动信号微弱的故障发生初期，从而及时地发现故障，提高故障检测的准确性和置信度。但是也存在一些问题，由于第二代小波是利用提升模式构造成的，构造的方案有很多，针对不同研究对象的特点，怎样选择最合理的提升方案还需要进一步研究。

[1]Sweldens W. The lifting scheme. A construction of second generation wavelet[J]. SIAM J Math Anal,1997, 29(2): 511-546.

[2]周林成, 杨慧中. 基于二代小波变换的信号去噪及其软测量建模[J]. 计算机与应用化学, 2008, 25（7）: 823-826.

[3]付华, 尹丽娜. 小波包分解在电机故障诊断中的应用[J]. 微电机, 2007, 40(5):86-89.

[4]刘树春, 潘紫薇. 第二代小波在振动信号去噪中新方法的研究[J]. 机械传动, 2008, （4）：64-65.

[5]Daubechies and Sweldens. Factoring wavelet transform into lifting steps[J]. Fourier Anal App,1998, 4(3)：247-269.

[6]王芳，鲁顺昌. 基于小波包分析的电机故障检测[J].电机与控制应用，2008，35（7）:52-54.

[7]郭晓霞，杨慧中. 小波去噪中软硬阈值的一种改良折衷法[J]. 智能系统学报，2008, 3（3）:222-225.

[8]DONOHO D I, JOHNSTONE IM. Adapting to unknown smoothness via wavelet shrinkage[J].Journal of American Stat A ssoc, 1995, 12(90):1200-1224.

[9]高成. Matlab小波分析与应用（第二版）[M]. 国防工业出版社，2007: 210-228.