半(非)参数模型和抗差M估计法在多波束测深数据误差处理中的应用

朱振华

(广州海洋地质调查局，广州 510760)

1 概述

剔除了明显粗差的河道多波束测量数据中，其边缘波束尤其近岸测量条带边缘波束由于缺乏校正手段，受到的系统误差影响较大。为了提高该部分数据精度，必须对其系统误差和小粗差进行处理。由于系统误差的影响，本来的正确数据可能被认为是小粗差，原本是小粗差的点可能被遮蔽而作为正确数据，因此，在数据存在若干人工检测点的情况下，本文采用半(非)参数法先处理系统误差并修正高程值后再以抗差M估计法检测异常，期望在最大程度上还原真实水深值。

2 半(非)参数模型

在内河声纳测量中，系统误差的主要来源是测船横摇。由于声纳测量属于动态测量，观测结果存在着无法参数化的系统误差。半参数模型为解决此类问题提供了可行之道，该模型表达为间接平差模型的延伸:

式中:L和Δ为n维观测向量，Δ～(0，σ2)是观测误差向量，x为参数向量，B为列满秩矩阵，S=[s1，s2，…，sn]T是一非参数待定量，作为系统误差的描述。列出其误差方程为:

由最小二乘原理VTPV=min求得的法方程只有t个方程，无法确定S和Δ的估值。根据Fisher和Hegland(1999)的观点[1-2]，给出补偿最小二乘准则为:

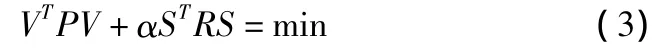
式中:R为正规化矩阵，α称为规范化参数或平滑因子。以式(2)为条件，由拉格朗日乘常数法构造函数:令，经过一系列推导可得:

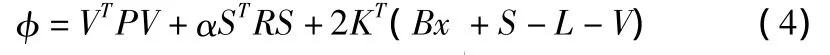
其中 N=BTPB，M=P+αR-PBN-1BTP。由文献[1]和[2]的观点，取:

G的定义请见上述文献。由于rank(R=n-1＜n)，需要增加一个约束条件再次由拉格朗日乘常数法构造函数求条件极值。当测船在变化平缓的河道以较慢速度测量时，可以认为一个横摇期间所测量的河床点实际高程相等，而横摇是周期性运动，在一次横摇中对高程值的正负影响基本相互抵消，在一定范围测区内可将系统误差之和看作零，即，得:

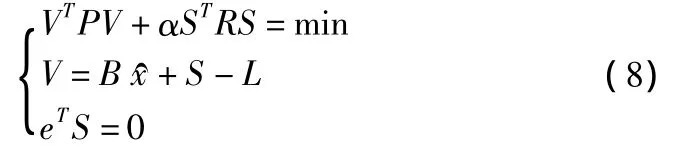
拉格朗日函数为:

令W=P-PBN-1BTP，推导得到式(8)的解:

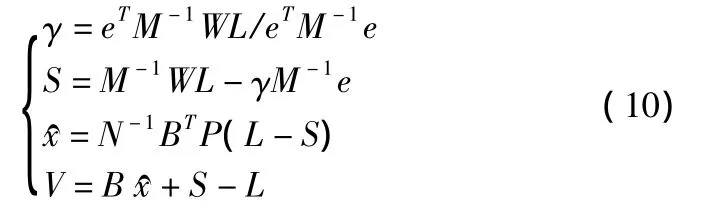
确定S的估值和正规化矩阵R后，采用L-曲线法确定α的值。以一小段河道为例，当在近岸处人工测量若干深度并作为真值)z代替式(1)中的Bx，即以检测点的真误差l=z-)z为观测值时，系统误差为S，观测噪声为Δ，则可以将式(1)的系数阵看作零，这时称为非参数估计，式(1)可表达为:

分别由式(10)、式(11)可推出:

其中 M=PαR，γ =eTM-1WL/(eTM-1e)，W=P=E。对由式(13)确定的系统误差向量S，建立如下函数关系:

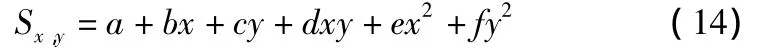
将该河段边缘波束共数千个原始数据代入上式，即可求得各点的系统误差。表1中x为横坐标，y为纵坐标，为方便起见，纵横坐标分别省去前面三、四位数字，即各点原坐标应为(455***.**，3799***，**)，z为多波束测深值，)z为同一平面坐标的人工测量值，共21个。S1为非参数法去除的系统误差。

3 抗差M估计滤波法

根据黄谟涛的观点[3]，基于M估计的抗差解为:

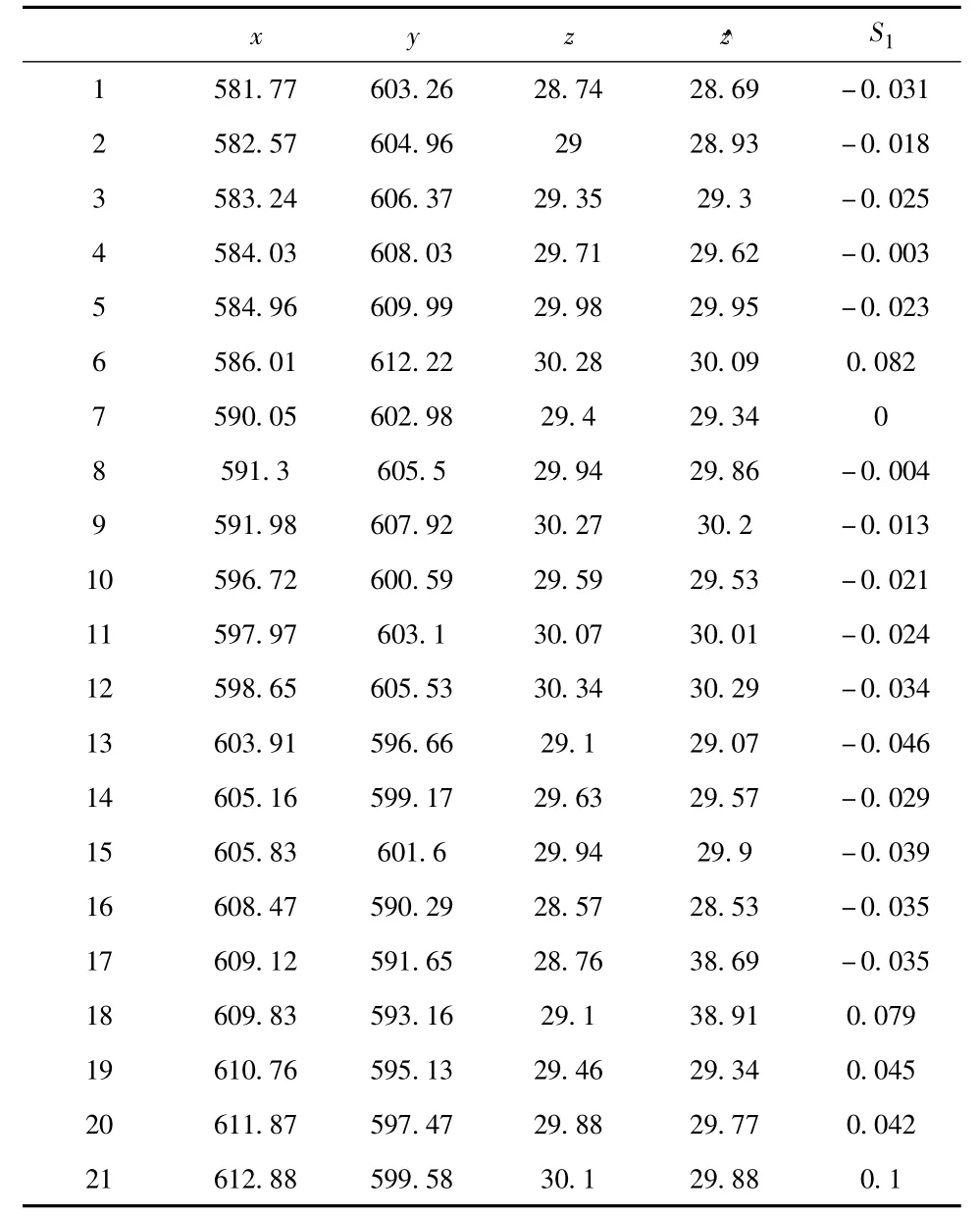
表1 两种方法去除的系统误差对比 m

第k+1步迭代解为:

式中:A为方程系数矩阵，L是自由项，X为模型待定参数向量，pi为观测值的权，为等价权阵。等价权值pi采用杨元喜提出的 IGGⅢ[4]方案:

式中:v′i=vi/，k0和 k1分别取 1.0 ～1.5 和 2.0 ～3.0，权值由上一次迭代得到的加权平均值计算残差，再判断比较条件来确定。k次迭代后的为:

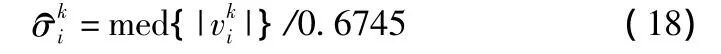
由迭代解表达式，设受检测点邻域内某点深度为zi(i=1，…，m)，可得基于抗差M估计的选权迭代加权平均值计算公式如下:

4 结论与建议

去除系统误差后，高程的歪曲现象得以暴露。高程的歪曲包括粗差遮蔽和高程放大，即去除系统误差前，某些点会被错误判断为异常或原本属于怀疑异常点却被漏检。系统误差被去除后，点的真值最近似值就得以还原。因此，沿用2节中的例子，对去除系统误差后的示例数据进行小异常的检测。取所有迭代权稳定后为迭代停止条件，用抗差M估计法筛选异常值。表2是去除系统误差前后提取异常值的对比，而图1是去除系统误差前后实验河段原始数据及异常值分布图，借助 MATLAB 显示[6]。

表2中可以看到，去除系统误差前筛选到8个异常值，去除系统误差后筛选到9个异常值，在去除系统误差前后筛选的所有异常值中，前7个异常值都被检测到，它们的平面坐标一致。去除系统误差前筛选到的第8个点(加粗显示)因受到系统误差影响导致高程被放大而被误列为异常点，该点去除系统误差后高程为30.05 m;去除系统误差后筛选到的第8、9个异常点(加粗显示)在去除系统误差前因受到系统误差遮蔽而未被检测到，其实际高程值分别为30.17 m和30.39 m。图1中(a)和(b)中黑色点分别为表2中所筛选的异常值。

从上述结果可以看出，本文所采用的两种方法在处理河道多波束测量数据高程误差歪曲现象中取得了良好的效果，同时有效地修正了高程值。但是该处理方法也存在一定的缺点，目前只在变化平缓的河道可以取得较好的效果，应进一步改善算法，使其局限性得以突破。

表2 去除系统误差前后筛选的异常值

图1 去除系统误差前后剔除的异常值示意图

[1] 胡昌宏.半参数模型的估计方法及其应用[D].武汉大学博士学位论文，2004.

[2] 孙海燕，吴云.半参数回归与模型精化[J].武汉大学学报信息科学版.2002，27(2):172-174.

[3] 黄谟涛，翟国君，王瑞，欧阳永忠，管铮.海洋测量中异常数据的定位研究[J]. 海洋测绘，1999，(2):10-19.

[4] 杨元喜.抗差估计理论及其应用[M].北京:八一出版社，1993.

[5] 赵建虎.多波束深度及图像数据处理方法研究[D].武汉大学博士学位论文，2000.

[6] 王红，邸国辉，熊燕.水下地形测量高程异常点剔除方法研究[J]. 四川测绘，2004，27(1):36-38.