基于偏最小二乘回归法的电站锅炉炉膛出口烟温调整试验研究
秦宇飞, 白 焰, 钟艳辉, 王 潇, 李晓忠, 王天刚, 张菊军
(1.华北电力大学能源与动力工程学院,北京102206;2.华北电力科学研究院有限责任公司,北京100045;3.西北电力设计院,西安710075)
我国许多电厂由于煤质变化、设备改造和变负 荷运行等原因,没有达到最佳的燃烧效果.为改善燃烧效果,可以通过大量的正交试验获得合理的计算机控制曲线,但是耗时较长、成本较高;也可以利用燃烧理论对燃烧过程进行数值模拟和理论建模,但计算量大,特别当有些机理不太清楚时,难以建立完善的模型.随着人工智能技术的发展,人工神经网络[1]和遗传算法[2]等逐渐在建模中使用,但是建立的模型对所描述对象的输入输出变量之间的关系往往缺乏很好的解释,电厂工作人员不易掌握.由于煤粉颗粒在电站锅炉炉内的燃烧过程非常复杂,受煤种、煤粉的浓度和细度、各次风比例、燃烧器和炉膛布置等因素的影响,这些因素之间又存在大量的耦合关系,在自变量数量很多的情况下建模,变量之间往往呈现出较高的相关性,增加了数据分析和建模的难度.统计学理论在处理大量数据方面有很大优势,适合研究从实际对象得到的大量数据,与其他方法相比,方法简单、计算快捷,更易被现场工作人员掌握.偏最小二乘回归(PLS)是一种新的多元统计方法,被称为第二代回归分析方法[3].偏最小二乘回归法吸取了主成分回归法提取主成分的思想,但主成分回归法只是从自变量中去寻找主成分,与因变量无关,而偏最小二乘回归法则是从因变量出发,选择与因变量相关性较强而又方便运算的自变量的线性组合,同时克服了自变量之间多重相关性的问题,因此计算结果更为可靠,在实际系统中的可解释性也更强.与传统的回归分析、主成分回归方法相比,该方法具有更大的优势,可使模型精度、稳健性、实用性都得到提高[4].
1 试验锅炉概况
试验对象为HG-670/140-9型一次中间再热、单汽包自然循环锅炉,配套200 MW汽轮发电机组.锅炉呈∏型布置,采用全辐射型的前屏过热器,半辐射型的后屏过热器.过热蒸汽温度采用二级喷水减温调节,再热蒸汽温度主要以汽-汽交换器调节.燃烧器为四角双切圆布置的水平浓淡直流燃烧器,设计假想切圆直径分别为 φ 1 200和 φ 600,共 16支分四层布置,每组燃烧器有4个一次风喷口、6个二次风喷口.设计一次风速为30.5 m/s,一次风率为31.2%;设计二次风速为48 m/s,二次风率为64.4%.该锅炉近年出现了一些运行问题,如过热器和再热器爆管、减温水量大、空气预热器堵灰等,有些问题是燃用煤种偏离设计煤种造成的[5-6].炉膛出口烟温是锅炉设计和性能监视的重要指标[7],可提前反映燃烧工况的变化.如果炉膛出口烟温大幅偏离设计值,则容易出现上述部分问题.因此,通过调节炉膛出口烟温,可改善锅炉运行水平.
2 试验部分
2.1 试验设计思想
通常,反映锅炉系统运行状态的变量可以概括为3种,如图1所示.

图1 锅炉系统运行状态的变量类型Fig.1 Types of variables fo r operational status of boiler system
输入变量是可以被直接调节和控制的变量,如氧量、风量等;输出变量是涉及锅炉运行效果的变量,如煤耗率、主蒸汽流量、飞灰含碳量等;中间变量是介于输入变量和输出变量之间的变量,反映了锅炉运行的中间状态,可提前反映运行效果.如果可以监视关键的中间变量,并建立这些中间变量和输出变量的关系,那么就能通过控制中间变量来控制输出变量.炉膛出口烟温的测点通常位于炉内辐射换热与对流换热的过渡区,能够快速反映风量、氧量调节的变化,同时也能提前反映燃烧效果,因此认为其是典型的中间变量.
通过设定的试验采集运行数据,以及进行偏最小二乘回归分析,建立炉膛出口烟温的PLS模型.在分析模型影响因子之后,进一步调整运行参数,以获得试验数据,并利用优化软件分析,计算出最佳工作点.
2.2 试验数据采集方法及内容
试验的前提条件是要保证煤质稳定.试验期间这台机组还带着当地的热网,所以在主蒸汽流量为580 t/h、540 t/h和490 t/h负荷条件下进行试验,以上负荷分别代表高、中、低负荷.
2.2.1 采集数据的选择
为了减少计算量及便于分析,回归分析使用的变量不能太多,因此需要对锅炉的变量进行筛选.试验机组共有3 000个测点,炉侧约有1 500个.试验采用相关分析、逐步回归分析和最佳子集等多元回归分析方法初步确定与燃烧有关的变量;然后结合电站锅炉的运行经验(如不同的配风和配煤方式对炉膛出口烟温影响较大[8]),选择了部分有代表性的变量参与回归分析,包括炉膛出口氧量、各层给粉机转速、各层风门挡板开度、各层风压和风温等[9].影响炉膛出口烟温的其他因素有:主蒸汽流量与温度、炉膛漏风、煤质等.此外,为观察调节效果,还需要采集送引风机电流、减温水流量等数据.
氧量的选择可以说明使用相关分析选择变量的方法.对氧量与引风机电流、送风机电流等变量进行相关分析,得到Pearson相关系数(表1).
由表1可知,氧量与送引风机电流、二次风挡板阀位、送风机风压和送风机风量存在多重共线性.从锅炉运行原理与工程实践经验来看,一次风率对炉膛出口烟温有一定影响.而试验对象没有一次风机,试验中一次风挡板不参与调节,一次风率主要与送风机风量和风压有关,因此认为一次风率与氧量也存在多重共线性.虽然使用PLS可以克服自变量中多重共线性的影响,但是为了减少自变量的数量,只选择了氧量,而没有选择风机电流等变量.
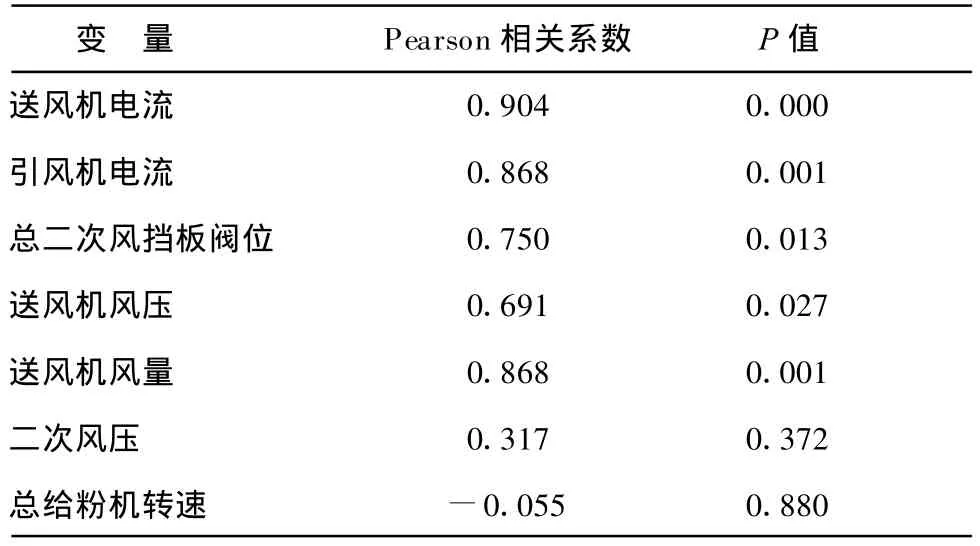
表1 氧量与部分运行参数的相关性Tab.1 The correlation of oxygen content with part of the operational parameters
2.2.2 数据采集
(1)常规参数采集
为了实时观测试验过程以及分析试验数据,抽取了大约200个测点进行观测.部分测点的数值需要经过计算得到,如减温水总量和主蒸汽温度平均值等.为了保证DCS运行安全,数据从SIS系统中获取.
(2)炉膛出口烟温测量
将红外线远程测温仪设置在折焰角下方的炉膛看火孔,试验时每5 min记录一次温度值.
(3)原煤取样
每组试验前,在甲、乙侧给煤机处取样,并进行工业分析,用于衡量煤质的变化.
(4)灰取样
为评价燃烧效果,每次试验均需要测量飞灰含碳量.因现场没有在线的飞灰测量设备,所以采用人工在排灰口取样.取样后,交由电厂化验室进行飞灰含碳量分析.
2.3 试验步骤
在3个不同的负荷下进行试验,得出相应的回归方程.每个工况取10组左右数据,每次执行操作后,待工况稳定,再进行数据记录和取灰,锅炉运行数据的采集间隔为10 min或15 min.具体试验步骤如下:
(1)试验准备.做好数据记录准备;试验之前需吹灰,以减少因炉内结渣和积灰产生的误差.
(2)在试验负荷下,稳定工况.将工况稳定时的参数作为试验对比的基准值,该参数也是电厂操作人员在各负荷段的常规运行值.
(3)在保证安全的前提下进行试验,大范围调整自变量.这样可以降低回归系数的波动范围,增加回归系数的稳定性.锅炉的最佳运行点往往在接近临界值的位置,主要包括:二次风挡板、氧量以及各层燃烧器煤粉量的调整.
(4)对得到的试验数据进行选择及偏最小二乘回归分析.如果认为回归方程不准确,可以增加中间点,进行分段线性化.根据分析结果,再进行燃烧调整试验,获得试验数据.
(5)根据试验数据,利用优化软件寻找优化值.
(6)锅炉在优化值下运行,进行试验验证.
3 建模及分析
利用偏最小二乘回归法建模时,在自变量系统X中,提取一个主成分t1,在因变量系统Y中,提取一个主成分u1,要求:①t1和u1应尽可能多地携带数据集中的变异信息;②t1和u1的相关程度最大.第1个主成分被提取后,分别实施X对t1和Y对u1的回归,如果回归方程已经达到要求的精度,则算法终止;否则,利用 X被t1解释后的残余信息以及Y被u1解释后的残余信息进行第2次主成分提取,直到达到满意的精度.
目前已有成熟的统计学分析软件用于偏最小二乘分析,本文使用Minitab软件,以主蒸汽流量490 t/h(低负荷)为例来说明偏最小二乘回归方法的数据分析过程.
3.1 异常值检验
采集到的运行数据可能存在部分异常值,在对数据进行分析之前,需要将异常值去除.首先利用观测值标准化残差(Studentized Residual)与Leverage值的关系图来判断采样数据是否为异常值.Leverage值用来衡量一组数据对整个数据集的影响[3],如果其值太大,表示具有远离零点的X分值,回归模型对该样本的依赖性较大,不利于模型的稳定,也即此组数据可能异常.标准化残差可以在避开 Leverage值的条件下,考虑观测值的差别,从而保证相关图横纵坐标的独立性.Leverage值hi的计算公式如下:

式中:T是X的分量矩阵;n是数据的个数.
标准化残差ri的计算公式如下:

式中:ei是第i个残差;S2是均方误差.
计算各样本数据炉膛出口烟温的标准化残差与Leverage值,得到的散点图示于图2.

图2 标准化残差与Leverage值(3个分量)Fig.2 P LS standardized residuals and leverage values(3 components)
通常使用的异常值检验标准为:观测值的Leverage值大于2 m/n(m为分量数,n为观测值数),本分析中m=3,n=12;标准化残差大于2以及小于-2.从图2可以看出,所有12组数据的标准化残差均满足要求,只有第1组和第5组的Leverage值大于0.5,这2组数据被判断为异常.由于烟气扰动的影响,利用红外测温仪观测到的温度值会有较大的波动,有时波动范围可能达到30 K,这易于将异常值记录下来.在偏最小二乘回归分析时,将以上2组数据去除.
3.2 确定模型主成分数
去除采样数据异常值后,利用偏最小二乘回归法对炉膛出口烟温进行建模.采用交叉验证的方法确定建模所用主成分数,交叉验证采用逐一剔除法[10].经过交叉验证确定的PLS模型的最佳主成分数为3(图3).
最优模型结果为:R-Sq(残差的平方和,residual-square)=85%,PRESS(预报残差平方和,prediction residual error sum of squares)=23 704.RSq是指模型中可以解释的变动部分占总变动的比率,代表了模型中因素对结果的解释能力.85%能够满足PLS建模的需要[10].
利用建立的模型预测17个样品,得到模型计算值与真实值的关系(图4),其Pearson相关系数为0.941,均方根误差RMSE=15.2.

图3 采用交叉验证方法确定的PLS模型的主成分数Fig.3 T he number of main components of PLS model determined by cross validation method
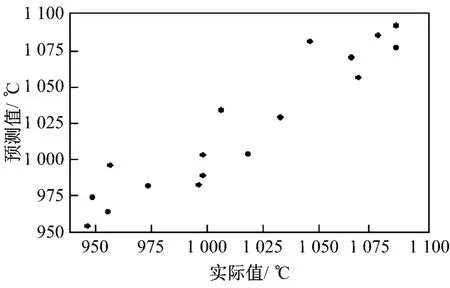
图4 P LS模型预测值与实际值的散点图Fig.4 Scatter diagram of fo recast values by P LS model and actual values
3.3 回归系数分析
表2列出了采用偏最小二乘回归法计算得到的回归系数.为了便于分析预测模型各影响因子对预测结果的贡献以及消除变量单位对数值的影响,表2也列出了相应的标准化回归系数.

表2 主蒸汽流量为490 t/h时采用偏最小二乘法计算得到的回归系数Tab.2 The regression coefficient calculated by PLS method when the flow rate of the main steam is 490 t/h
由表2可知:
(1)氧量的标准化回归系数约为-0.12,说明炉膛出口烟温对氧量很敏感,减少氧量会提高炉膛出口烟温,进而影响过热器、再热器壁温和汽温.在调节氧量时,应密切关注受热面温度和结焦情况[11].减氧会导致锅炉受热而结焦,需要安排合适的时间吹灰,虽然吹灰会损失一部分蒸汽,但是与减氧获得的经济性相比小得多.因为每减少1%的过氧量,大约会减少煤耗1.06 g,所以减少氧量对燃烧调节优化有重要作用.在低负荷条件下进行氧量调整,应考虑燃烧的稳定性;在高负荷条件下进行氧量调整,应考虑燃烧的经济性.
(2)一层给粉机转速的标准化回归系数为0.09,相对其他层偏大.本组试验数据属于低负荷数据,一层给粉机在最下层,为燃烧提供“底火”,各层燃烧的着火性能自下而上逐渐改善.下面已着火的气流对上面的气流有点燃作用,影响了火焰中心的位置.因此可以认为,当该锅炉的给粉机转速为倒三角时,会起到“抬火”作用.
(3)二次风挡板阀位的平均标准化回归系数约为-0.10,因此各二次风叠加之后对燃烧影响较大.关小二次风挡板可降低炉膛出口烟温,同时也减少氧量.试验得出的二次风压的标准化回归系数较小,因此可以维持或少量提高原二次风压.二次风挡板阀位标准化回归系数在-0.08~-0.11.下层二次风量大时会加强煤粉扰动,上层二次风量大时会压住火焰,均可以降低炉膛出口烟温.
3.4 可调参数组合及调整
通过偏最小二乘回归分析可知,一层给粉机转速对炉膛出口烟温有较大影响.后期试验采用增强“底火”的方法,将一层给粉机由3台增加到4台,平均转速从333 r/min增加到342 r/min.同时改变上层给粉机转速,将原来的倒三角燃烧方式改为缩腰型.增加一层给粉机粉量的同时,降低下部二次风执行器阀位,二、三层二次风阀位平均降低20%.燃烧器的煤粉先与较少的二次风混合,再与较多(上部)的二次风混合,这样可提高炉膛出口烟温,同时可改善低负荷时过热和再热汽温.
3.5 最佳工作点
通过调节炉膛出口烟温和减少氧量等大范围变工况试验,使获取的试验数据包含了潜在的最佳工作点.使用比较成熟的BP神经网络优化方法寻找最佳工作点,得出在3种负荷下可调参数的运行值.可调参数的试验优化值与基准值的对比示于表3.获得3种负荷下的运行点后,采用线性插值的方法,可以计算出中间各负荷的可调参数.

表3 主要可调参数的优化值与基准值比较Tab.3 Comparison between the optimized values and the base values of the main adjustable parameters
4 试验验证
锅炉在最佳工作点的可调参数下运行,得到在3种不同负荷下的运行参数优化值,结果示于表4.虽然部分指标略有下降,但是从减少煤耗的角度来看,试验优化值提升了锅炉的整体性能.通过对炉膛出口烟温的调节,氧量平均降低1.4%,煤耗减少约为1.5 g/(kW◦h).排烟氧量与氧量有较大相关性,对煤耗的影响已通过氧量体现.按照试验优化值运行一段时间后,从SIS系统的发电厂性能计算模块里可看出,供电煤耗已减少2 g/(kW◦h)以上.
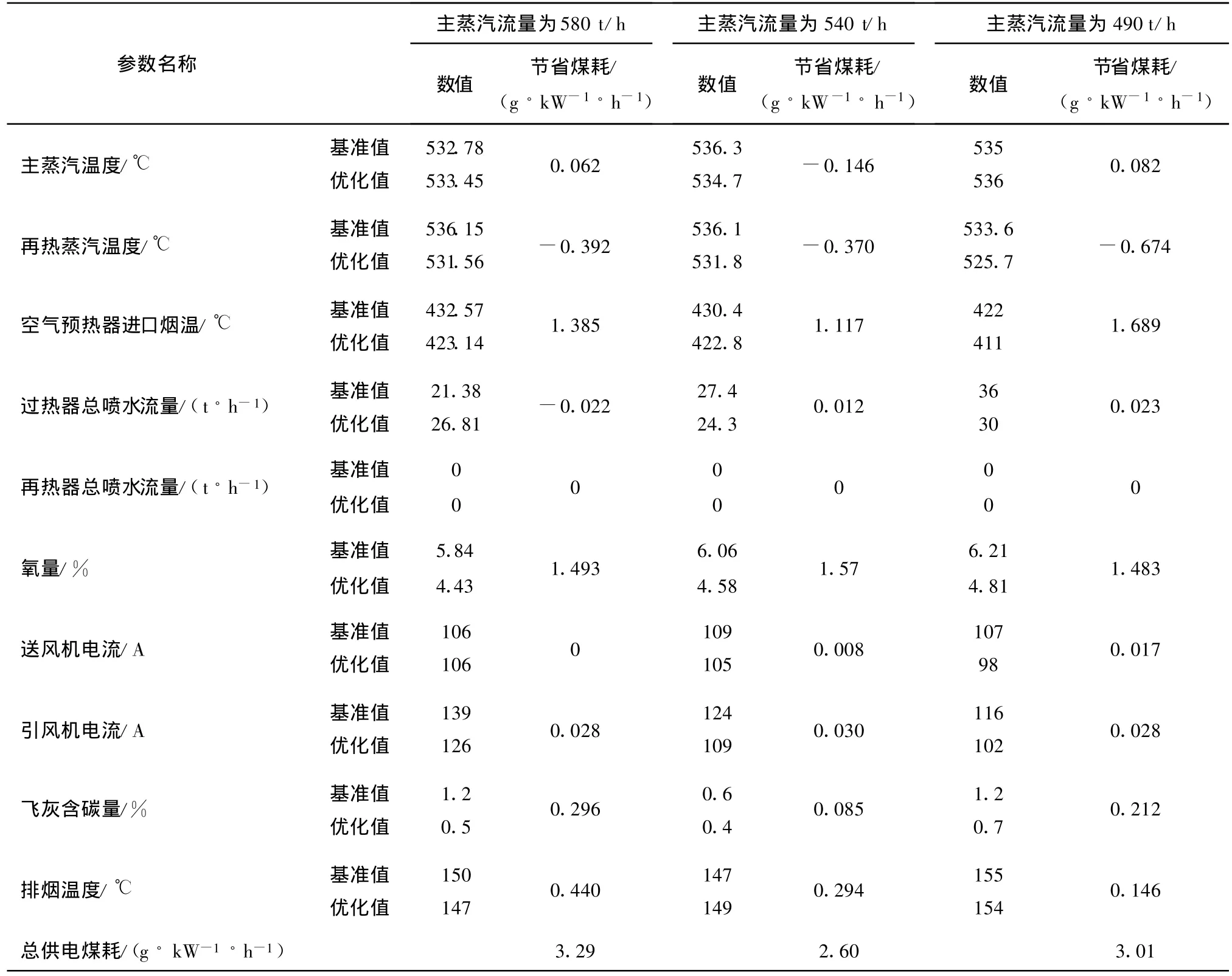
表4 主要运行参数的试验优化值与基准值的比较Tab.4 Comparison between the experimental optimization values and base values of the main operational parameters
5 结 论
通过偏最小二乘回归分析,可以掌握锅炉运行指标与可调参数间的关系,对一些运行经验进行量化,使运行人员快速地掌握被调对象的运行特性,为锅炉燃烧优化先进控制策略的应用提供数据基础.此外,偏最小二乘回归方法克服了变量之间的多重共线性,适合锅炉这种复杂对象的运行参数分析.
[1]KALOGIROU Soteris A.Artificial intelligence for the modeling and control of combustion processes:a review[J].Progress in Energy and Combustion Science,2003,29(6):515-516.
[2]周昊,朱洪波,曾庭华,等.基于遗传算法的燃煤锅炉热效率优化[J].中国电机工程学报,2002,22(7):125-129.
[3]高惠璇.应用多元统计分析[M].北京:北京大学出版社,2005:22-55.
[4]尹力,刘强,王惠文.偏最小二乘相关算法在系统建模中的两类典型应用[J].系统仿真学报,2003,15(1):135-138.
[5]岑可法,樊建人,池作和,等.锅炉和热交换器的积灰、结渣、磨损和腐蚀的防止原理与计算[M].北京:科学出版社.1994:72-89.
[6]闫顺林,李永华,周兰欣.电站锅炉排烟温度升高原因的归类分析[J].中国电力,2000,33(6):20-22.
[7]岑可法,周昊,池作和.大型电站锅炉安全及优化运行技术[M].北京:中国电力出版社,2007:125-168.
[8]岑可法.锅炉燃烧试验研究方法及测量技术[M].北京:水利电力出版社,1987:75-79.
[9]李永华,陈鸿伟,孟凡军.300 MW锅炉优化燃烧调整试验研究[J].中国电机工程学报,2004,24(1):216-220.
[10]王惠文,吴载斌,孟洁.偏最小二乘回归的线性与非线性方法[M].北京:国防工业出版社,2006:25-46.
[11]吴安,曹汉鼎,马东森,等.华能德州电厂锅炉再热汽温偏低的原因分析及解决方案[J].动力工程,2008,28(6):839-846.

