管内插入网状肋强化换热的数值研究
张国立, 杨 立, 孙丰瑞, 张 健
(海军工程大学动力工程系,武汉430033)
流动与热交换现象大量地出现在能源与动力领域中,长期以来强化热量传递过程是人们所关注的重要课题.强化传热技术可分为主动式和被动式2类[1],被动式强化传热技术除流体输送的功耗外,无需附加额外动力,因此应用范围较广,对其的研究也较为深入和集中.几十年来,人们进行了大量的理论与试验研究,发展了多种强化传热技术,这些技术在各个领域均有广泛的应用.目前,常用的强化对流换热措施主要是减小热边界层的厚度、增强流体的扰动和增大近壁面的温度梯度[2-3].层流流动的温降发生在整个流动截面上,因此其强化换热的措施主要是:使流体产生强烈的径向运动以加强流体的混合,从而使中心处流体的速度和温度趋于均匀,增大壁面附近的温度梯度.管内插入肋可以显著地改善换热,但同时流动阻力也会增加.
由于气体的传热性能很差,因此如何强化气体侧的换热是学术界与工程技术领域的一个重要研究课题.目前,针对管内插入肋、纽带、翅片、螺旋线和旋流片等的研究较多.Zeitoun等[4]和Campo等[5]研究了带纵肋的套管内肋高及其组合变化对流动和换热的影响,并给出了拟合公式;赵钦新等[6]对管内插入翅片的流动和换热特性进行了研究.但针对管内插入网状肋的研究则较少,尚未见采用数值模拟对其进行研究的文献.通过对管内插入网状肋的流动和换热特性进行数值模拟,可以进一步了解其强化换热机理,促进其工业化应用.笔者针对高温气体流过圆管的强化传热问题,对圆管内插入网状肋的流动与换热特性进行了数值模拟,分析了肋的形状、网格间距、直径以及流体与固体的导热系数比kf/ks对换热和压力损失的影响,以寻求最佳的运行工况.
1 计算模型及方法
1.1 简化的物理模型
图1给出了管内插入网状肋的几何模型.其中,肋的类型有2种,即圆形网状肋和方形网状肋.圆形网状肋是由圆柱体垂直排列组成的网状结构,方形网状肋是由长方体垂直排列组成的网状结构.肋和管壁的材料均为铜,圆管直径为300 mm,长度为1 800 mm,选取其中一段长为100 mm的管段作为换热区域,忽略壁厚的影响.肋布置在换热区域内靠近入口侧,且与管壁是相连的实体,肋的形状、网格间距及直径取不同的参数.

图1 管内插入网状肋的几何模型Fig.1 Geometric model of the reticulated rib inserted in the pipe
1.2 数学模型及边界条件
假设管内流体为不可压缩的高温空气,其在管内的流速较低,流动处于层流状态,且流动过程是稳态的.不可压缩流体的三维、稳态、常物性连续性方程、动量方程和能量方程(无内热源)分别为:
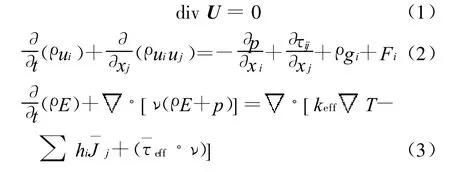
高温空气从圆管一侧进入,入口条件为速度入口边界条件,温度为T,流速为v;出口位于圆管的另一侧,出口条件为压力出口边界条件,设其表压为零;管壁为恒壁温边界条件,且管壁温度低于入口空气温度.
1.3 网格划分及数值方法
网格划分采用非结构的四面体和六面体混合型,网格数量为187万.为了获得稳定的速度场与温度场,计算区域从通道入口向上游延长,从通道出口向下游延长.为了进行比较,对没有肋的圆管通道也进行了计算.利用Fluent 6.1分离隐式求解器对方程进行求解,控制方程的离散采用控制容积积分法,其中对流项的离散采用一阶迎风格式,扩散项的离散采用中心差分格式,压力和速度的耦合采用Simple算法.解收敛的判断标准是相对残差小于1×10-6.计算的介质为空气,其 Pr为0.677.
2 结果与分析
2.1 速度分布
图2为管内插入网状肋后距离肋10 mm处的无量纲速度分布曲线,其中u0为截面平均速度,h为肋的网格间距.由图2可知,光管内的无量纲速度波动很小,管内插入网状肋后,流体产生强烈的扰动,无量纲速度波动较大,这是由于流体流过网状肋时产生了很强的径向运动.肋的间距越小,流体的扰动范围越大,扰动的频率越高.
2.2 阻力损失
图3给出了管内插入网状肋后无量纲阻力系数随网格间距和雷诺数的变化,其中f0为光管的阻力系数,f为管内插入网状肋的阻力系数.圆形网状肋的直径为 0.2 mm,方形网状肋的边长为 0.2 mm.从图3可知,随着网格间距的增大,阻力系数迅速减小,这主要是因为圆管中安装网状肋后对流体的流动会产生较大的局部阻力——形状阻力,而形状阻力是通道总阻力的主要来源.形状阻力的大小主要与阻流件的迎风面积有关,随着网格间距的增大,肋的迎风面积减小,因此阻力系数迅速减小.当网格间距h为10 mm时,阻力系数较大,且方形网状肋的阻力系数大于圆形网状肋;当网格间距h为20 mm时,阻力系数迅速减小,之后随着网格间距的增大,阻力系数减小的幅度下降.

图2 无量纲速度分布Fig.2 Dimensionless velocity distribution
2.3 温度分布
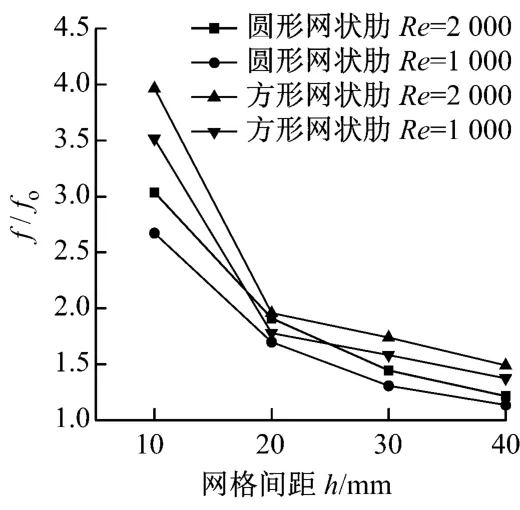
图3 f/f0随h的变化Fig.3 f/f0vs.h
影响圆管内温度分布的因素较多.图4为给定流速下,高温气体流过不同网格间距的圆形网状肋时的温度场分布.肋的直径为0.2 mm,网格间距h分别为10 mm 、20 mm 、30 mm 和40 mm.由图4可知,网格间距越小,则网状肋对圆管内流体的扰动越强,气体流过网状肋后温度场分布越均匀.由图中的温度等值线可以看出:网格间距较小时,气体流过网状肋时温降较大.根据场协同原理[8]可知,通过在圆管内加入网状肋对流体流动的速度场进行扰动,使速度矢量与温度梯度的夹角减小,从而强化了换热.
2.4 圆管内插入网状肋换热的影响因素
圆管内插入网状肋的出口平均温度为 Tout,光管出口的平均温度为 T0,出口无量纲温度定义为Tout/T0.影响换热的因素有肋的形状、肋的网格间距h、肋的直径Ds、雷诺数Re以及流体与固体的导热系数比kf/ks等,下面分析它们对换热的影响.

图4 流体流过圆形网状肋后的无量纲温度分布Fig.4 Dimensionless temperature distribution of the fluid when flowing through the circular reticulated rib
2.4.1 网格间距的影响
图5给出了网格间距h对出口无量纲温度的影响.由图5可知,在雷诺数相同的情况下,圆形网状肋和方形网状肋的出口无量纲温度都随着网格间距的增大而升高.这是因为网格间距增大后扰流减小,流体混合不充分导致场协同度减小,从而使换热减弱.在网格间距相同时,方形网状肋的换热效果比圆形网状肋的好.

图5 Tout/T0随h的变化Fig.5 Tout/T0vs.h
2.4.2 肋直径的影响
图6给出了圆形网状肋的网格间距h为30 mm时,出口无量纲温度随肋的直径Ds的变化.由图6可知,在网格间距一定时,随着肋直径的增大,网状肋中间的流动间隙变小,由流体力学基础知识可知肋的阻力增大,因此当流体流过直径较大的网状肋时受到的扰动更强,使得换热更加充分.
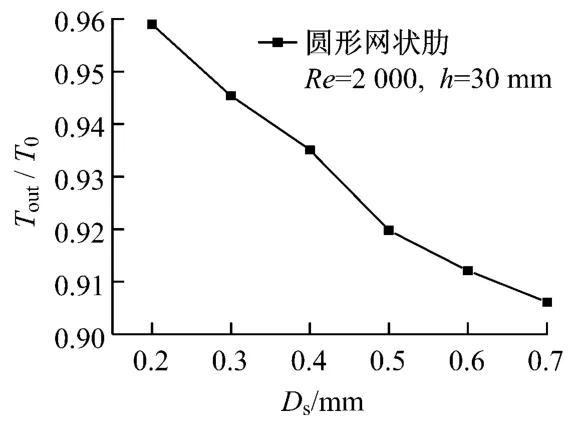
图6 Tout/T0随Ds的变化Fig.6 Tout/T0vs.Ds
2.4.3 雷诺数的影响
在不同网格间距下,出口无量纲温度随Re的变化示于图7.由图7可知,管内插入网状肋后,出口无量纲温度随着Re的增大而升高.无论是圆形网状肋还是方形网状肋,当网格间距为10 mm时,出口无量纲温度随Re的变化趋势最为明显.在8种网状肋中,方形网状肋在网格间距h为10 mm时换热效果最好,即在层流时,无论在什么样的流速下,网格间距为10 mm的方形网状肋均能使高温气体流过圆管后的出口温度最低.
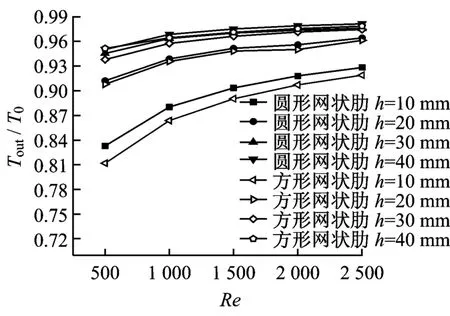
图7 Tout/T0随Re的变化Fig.7 Tout/T0vs.Re
2.4.4 导热系数比kf/ks的影响
图8给出了在网格间距为10 mm时,导热系数比kf/ks对管内插入圆形网状肋后出口无量纲温度的影响.由图8可以看出,随着kf/ks的增大,管内换热效果逐渐减弱.当kf/ks=1时,kf/ks对出口无量纲温度没有影响;当kf/ks<0.1时,随着kf/ks的减小,出口无量纲温度逐渐降低,且降低幅度很大,几乎呈直线下降趋势,这与文献[9]的结论基本吻合,说明网状肋对换热效果有重要影响.

图8 Tout/T0随kf/ks的变化Fig.8 Tout/T0vs.kf/ks
2.5 圆管内插入网状肋的性能评价
为了评价圆管内插入网状肋后换热与流动的综合性能,引入性能评价指标PEC[10]:

式中:Nufree为光管的努塞尔数;ffree为光管的阻力系数.
图9给出了PEC随Re的变化.由图9可知,随着Re的增大,PEC呈缓慢上升趋势.在不同Re下,PEC都大于1,说明管内插入网状肋可以很好地改善流动与换热的综合性能.在网格间距h为10 mm时,圆形网状肋的换热效果比方形网状肋的差,但其综合性能却优于方形网状肋,说明性能评价指标是一个综合指标,不能仅由换热性能决定.
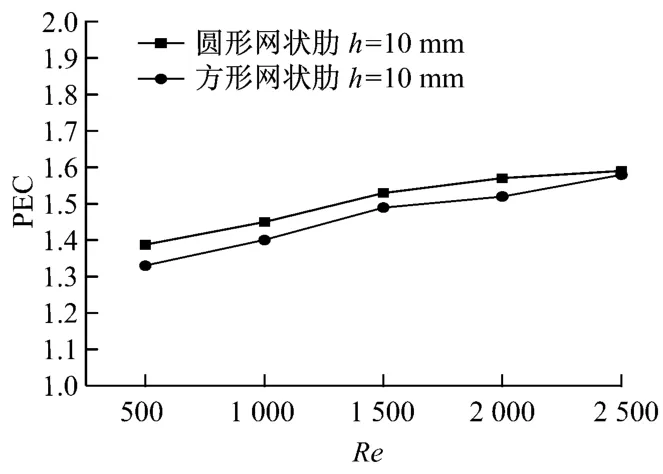
图9 PEC随Re的变化Fig.9 PEC vs.Re
3 结 论
(1)肋的形状对流动换热和阻力特性有一定的影响,在网格间距一定的情况下,方形网状肋的换热特性优于圆形网状肋,但其阻力损失较大.
(2)无论是方形网状肋还是圆形网状肋,随着网格间距的减小,换热特性均增强,但同时阻力系数均增大.
(3)管内的换热特性随着kf/ks的减小而增强,当kf/ks<0.01时,kf/ks对管内换热的影响较明显,此时减小kf/ks能得到较好的换热效果;当kf/ks>0.01时,kf/ks对管内换热的影响较小,此时减小kf/ks意义不大,在实际应用中可根据流体的性质来选择适当的肋材料.
(4)在网格间距一定的情况下,管内换热特性随肋直径的增大而加强,但同时阻力系数也迅速增大,在实际应用中应根据PEC值,权衡利弊进行选择.
[1]BERGLES A E.Some perspectives on enhanced heat transfer second generation heat transfer technology[J].ASME Journal of Heat Transfer,1988(110):1082-1096.
[2]BERGLES A E,LEE R A,M IKIC B B.Heat transfer in rough tubes with tape-generated swirl flow[J].ASME Journal of Heat Transfer,1969(91):443-450.
[3]WEBB R L,KIM N H.Principles of Enhanced Heat T ransfer[M].New York:Taylor&Francis,1995:30-50.
[4]ZEITOUN O,HEGAZY A S.Heat transfer for laminar flow in internally finned pipes with different fin heights and uniform wall temperature[J].Heat and Mass Transfer,2004,40(3/4):253-259.
[5]CAMPO A,CHANG J.Correlation equations for friction factors and convective coefficients in tubes containing bundles of internal longitudinal fins[J].Heat and Mass Transfer,1997,33(3):225-232.
[6]赵钦新,范庆伟,周屈兰,等.新型轴对称内翅管换热过程的数值模拟[J].动力工程,2008,28(6):906-910.
[7]陶文铨.数值传热学[M].2版.西安:西安交通大学出版社,2001.
[8]GUO Zeng-yuan,TAO Wen-quan,SHAH R K.The field synergy(coordination)principle and its applications in enhancing single phase convective heat transfer[J].Int.J.Heat Mass Transfer,2005,48(9):1797-1807.
[9]王崧,李志信,过增元.纤毛肋强化管内对流换热[J].清华大学学报,2000,40(4):55-57.
[10]WANG S,GUO Z Y,LI Z X.Heat transfer enhancement by using metallic filament insert in channel flow[J].Journal of Heat and Mass Transfer,2001,44(7):1373-1378.

