一种新型磁阻型螺旋线圈电磁发射器的仿真研究
杨栋 沈志 杨丽佳 刘振祥 欧阳建明 蒋雅琴
(国防科技大学理学院,长沙 410073)
1 引言
上个世纪中期开始,超高速(大于3km/s)发射技术一直是研究的热点。传统火炮受到火药燃气滞止声速的限制,其极限速度一般在2~3km/s附近,而电磁发射器的弹丸速度则没有这样的理论限制[1]。1961年,K.Thom和J.Norwood提出了一种螺旋线圈电磁发射器(HCEL)结构,并经过P.Mongeau、F.Williams和近年来美国密苏里-哥伦比亚大学T.G.Engel等人的研究,取得了显著进展[2-5]。
HCEL结构的优点主要是具有高电感梯度。要产生同样的受力,HCEL需要比导轨炮较小的电流;而且炮的烧蚀小,使用寿命长,且能量转化效率高[6]。理论上,精确的解析法求解加速力有一定困难,因为其中涉及到椭圆积分的计算,故必须采用基于有限元的数值计算方法[7]。本文采用HCEL的基本结构,将弹丸换成铁磁质内置式,设计了一种新型磁阻型电磁发射器。基于Maxwell 2D软件对磁阻型发射器弹丸受力的影响因素,如弹丸与驱动线圈相对位置、弹丸和驱动线圈尺寸、电流大小等,进行了静态模拟。
2 磁阻型发射器基本结构
磁阻型螺旋线圈电磁发射器的基本结构如图1,主要由铁磁质弹丸和驱动线圈组成。电刷使驱动线圈的一段通电,导电的驱动线圈和弹丸总是处于产生最大力的最佳位置。线圈与铁磁质弹丸上磁化电流的引力加速弹丸前进。

图1 磁阻型螺旋线圈电磁发射器基本结构示意图
3 仿真与设计
利用Maxwell2D进行参数化电磁场分析,驱动线圈材料选择为铜,总电流设为20kA(电流密度为7.67×108A/m2)。驱动线圈通电部分长度:16.3mm,线圈半径:9.7mm;铁磁质弹丸长度:16.3mm,弹丸半径:6.3mm,材料为纯铁。线圈绕线所用导线直径:1.6mm,线圈匝数为 8.5.其 Maxwell2D模型如图2。
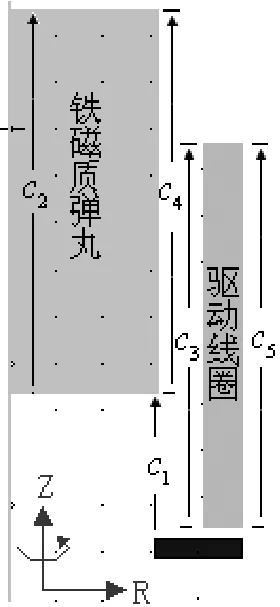
图2 磁阻型螺旋线圈电磁发射器的Maxwell 2D模型图
图2为轴对称的RZ平面模型,弹丸和驱动线圈均由图中的矩形旋转而成。当线圈匝密度较密时,可以将线圈作为一整块处理。C1~C5为几何约束变量,C2~C5用于改变弹丸和线圈长度,C1用于改变弹丸相对驱动线圈的位置。需添加扫描变量s和l,s代表弹丸与线圈轴向的中心距离,l表示线圈和弹丸的轴向长度。
3.1 弹丸与驱动线圈的相对位置对电感、受力的影响
磁阻型螺旋线圈发射器的弹丸与驱动线圈相对位置固定,分析弹丸的最大受力位置具有重要意义。电磁发射器的电能存储于电感中,而受力是电感储能的梯度。因此可以通过分析电感梯度随位置的变化规律来研究受力与位置的关系。
(1)受力
图3中,弹丸与驱动线圈重合时,弹丸受力为0,负号表示引力。弹丸相对线圈的位置不同,其所处的磁场不同,因此受力也不同。最大力位置在6.8mm处。

图3 铁磁质弹丸受力与位置的关系
(2)电感、电感梯度
Maxwell 2D仿真得到不同位置的互感,并利用Origin软件进行数据处理得到互感梯度随相对位置的关系,如图4所示。

图4 互感梯度与位置的关系
由于模型中将线圈作为一整块处理,所以仿真得到的电感值不是线圈的实际电感和互感值。对于自感,要将仿真值乘以线圈匝数的平方得到实际自感;对于互感,要将仿真值乘以线圈的匝数得到实际互感[8]。本文采用仿真值对图线分析没有影响。
分析图4发现,磁阻型发射器互感梯度曲线和弹丸受力曲线(图 3)形状相似,最大互感梯度值出现在 9.3mm位置附近,与其弹丸最大受力位置6.8mm偏移较大。其原因在于:由于铁磁质的存在,驱动线圈自感不再是常量。
铁磁质介质的存在,对驱动线圈自感产生影响,线圈自感不再为常量。线圈自感随铁磁质弹丸与线圈相对位置的变化曲线如图5。

图5 铁磁质弹丸的位置对驱动线圈自感的影响
由图5知,铁心位于线圈中心时,线圈自感最大。随着铁心离开中心位置,自感不断减小。
发射器系统产生的力定义为电感储能的梯度

其中,F为电磁力,Wi为炮内储存的感应电能。对于磁阻型螺旋线圈发射器

其中,Fhg为弹丸受力,Leq为弹丸-驱动线圈总的等效电感,为电感梯度,I为线圈每匝电流。
考虑弹丸-线圈总的等效电感Leq。

其中,La为弹丸自感,Ls为线圈自感,M为弹丸和线圈之间的互感。公式(3)中,弹丸与线圈磁场相加时互感项为正,而弹丸与线圈磁场相减时互感项为负。将(3)式对距离微分,Ls的微分不为0,得到铁磁质弹丸的受力公式

按照公式(4),利用Origin软件对数据重新进行处理,得到总等效电感梯度对位置曲线如图6。
由图 6分析可知,总等效电感梯度最大值位于7.7mm,与最大力位置(6.8mm处)接近。在电流不变的情况下,弹丸受力和互感梯度都只与相对位置有关。
3.2 弹丸、驱动线圈尺寸对最大受力的影响

图6 磁阻型螺旋线圈发射器总等效电感梯度与位置的关系
磁阻型螺旋线圈发射器弹丸的受力不仅与弹丸相对驱动线圈的位置有关,还与弹丸及驱动线圈的形状有关。影响受力的尺寸因素主要有:线圈、弹丸的长度和直径,线圈绕线的厚度和匝密度。一般在制造工艺满足要求的情况下,希望线圈与弹丸的间隙尽可能小,磁耦合紧密,能量转化效率高。本文设定线圈和弹丸的半径都不改变(即炮口径、线圈与弹丸的间隙固定不变),设定线圈的电流密度为7.67×108A/m2不变(匝密度不变时,每匝电流不变)。改变线圈、弹丸长度l但保持相等,仿真得到线圈不同轴向长度时弹丸的最大受力,如图7所示。

图7 弹丸最大受力与线圈轴向长度l的关系
图7表明,弹丸最大受力随线圈轴向长度的增大而增大,但增大趋势逐渐变缓。然而较长的线圈时间常数也较大,电流上升慢,使得最大加速力加速距离变短;且在同样的炮长情况下,较长的线圈加速时间也短。当驱动线圈轴向、径向长度比值达到2倍以后,受力增加显著变缓。
铁磁质弹丸的质量与弹丸长度成正比,而弹丸的最大受力随线圈长度的增加是先快后慢。因此,存在一个最佳线圈轴向、径向长度比值,使弹丸加速度最大。加速度正比于最大受力与线圈长度的比,如图8所示。
图8中,当线圈长度为10.5mm时(即驱动线圈轴向、径向长度比为1∶2),加速度为最大。对于同样的炮长 L,弹丸从静止开始以最大加速度值进行加速,则有
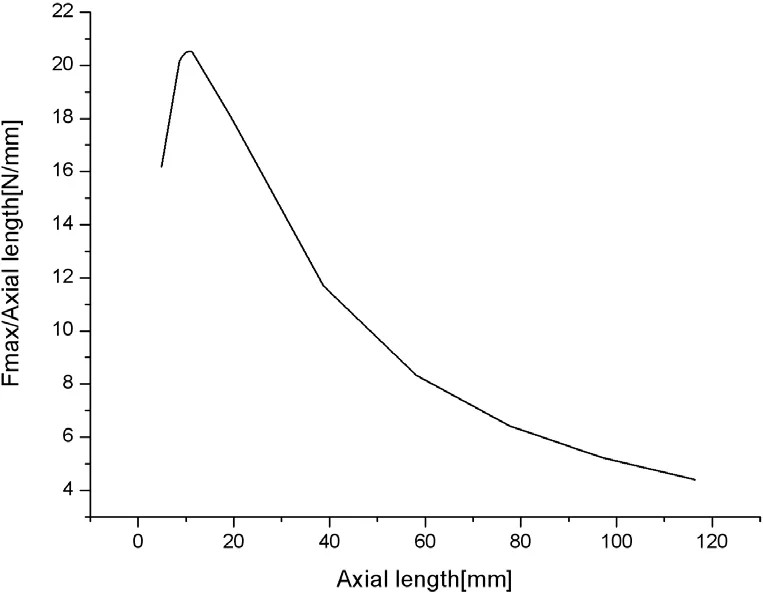
图8 弹丸加速度与线圈轴向长度关系

由(5)式知,加速度越大,弹丸炮口速度 v越大。实际设计中可以根据需要确定线圈长度,以达到最佳加速效果。
3.3 电流对最大受力的影响
磁阻型螺旋电磁发射器弹丸最大受力还与电流大小有关。改变线圈每匝电流大小,仿真得到弹丸最大受力如图9。

图9 弹丸最大受力与电流关系
当电流在2.5kA以下时,弹丸最大受力与线圈每匝电流平方成正比,;而当电流大于7kA时,铁磁质弹丸达到磁饱和,弹丸最大受力只与电流成正比。小电流时,最大受力位置随电流增大而增大,这主要是由铁磁质材料磁化的非线性所致。但当电流大于7kA时,最大受力位置基本不随电流变化。这是由于铁磁质磁化饱和,弹丸等效于通电电流不变的线圈,最大受力位置不再增加。从场的角度分析,弹丸达到磁饱和后,改变电流大小,只改变空间磁场的大小,并不改变磁场的相对分布。因此,磁阻型螺旋线圈电磁发射器应以适当的恒流方式工作。
4 结论
新型磁阻型螺旋线圈电磁发射器避免了感应型发射器的同步控制问题,电刷使驱动线圈的一段通电,驱动线圈和弹丸总是处于产生最大力的最佳位置。
本文利用 Maxwell 2D软件对弹丸受力的影响因素,如弹丸与驱动线圈相对位置、弹丸和驱动线圈尺寸、电流大小等,进行了静态模拟。结果表明:
(1)弹丸的受力大小与其相对驱动线圈的位置有关,且有一个最大受力位置。
(2)线圈半径固定时,弹丸最大受力随线圈轴向长度增大而增大,但增大趋势逐渐变缓。当线圈轴向、径向长度比值达到2倍以后,受力增加显著变缓。线圈轴向、径向长度比为 1∶2时铁磁质弹丸加速度达到最大。
(3)在电流较小的情况下,弹丸最大受力与线圈每匝电流平方成正比,最大受力位置随电流增大而增大;而铁磁质弹丸达到磁饱和后,弹丸最大受力只与电流成正比,最大受力位置不随电流变化。
仿真结果验证了HCEL的基本理论,并为磁阻型螺旋线圈电磁发射器结构的设计提供参考。
[1]王莹,肖峰.电炮原理[M].北京∶国防工业出版社,1995∶5.
[2]K. Thom and J. Norwood, “Theory of electromagnetic accelerator for achieving hypervelocities,” NASA,Tech. Note D-886, June 1961.
[3]P. Mongeau and F.Williams, “Helical rail glider launcher,” IEEE Trans.Magn., vol. MAG-18, pp.190–193, Jan. 1981.
[4]T. G. Engel et al., “Prediction and verification of electromagnetic forces in helical coil launchers,” IEEE Trans. Magn., vol. 39, pp. 112–115, Jan. 2003.
[5]T.G. Engel, et al., “Medium-bore helical-coil electromagnetic launcher with liquid nitrogen cooled armature,” to appear Proc. 15th IEEE International Pulsed Power Conference, June 2005.
[6]T.G. Engel, et al., “A Same-Scale Comparison of Electromagnetic Launchers,” IEEE, 2006.
[7]T.G. Engel, et al., “Efficiency and Scaling of Constant Inductance Gradient DC Electromagnetic Launchers,”IEEE Trans. Magn., vol. 42, Aug. 2006.
[8]卡兰塔罗夫, 采伊特林. 电感计算手册[M]. 北京∶机械工业出版社, 1992∶ 54.

