一种新型交流PI调节器及其在逆变电源中的应用
胡文华,马伟明,刘春喜
(1.华中科技大学 电气与电子工程学院,湖北 武汉 430074;2.华东交通大学 电气与电子工程学院,江西 南昌 330013;3.海军工程大学 电力电子技术研究所,湖北 武汉 430033;4.浙江大学 电气工程学院,浙江 杭州 310027)
1 引言
CVCF逆变器是不间断电源、中频电源、航空电源等许多设备的核心。在不同负载下保持恒定的输出电压是CVCF逆变器控制技术的主要目标。
CVCF逆变器的控制方法是当前电力电子领域的一个研究热点,目前已产生了多种控制方案。控制效果较好的主要有重复控制、无差拍控制、多环反馈控制这3种方法。重复控制[1]只需检测输出电压一个变量,稳态精度高,但设计过程十分复杂,目前还没有一种通用的设计方法。另外,重复控制器的工程实现也较为复杂,并且对控制芯片的存储容量有较高要求。无差拍控制动态性能极佳,但其设计过程依赖于精确的逆变器参数,所以它对逆变器参数变化十分敏感,这往往导致控制效果恶化,严重时,系统将可能不稳定,为了弥补这个缺陷,往往需要采用其他控制方法来进行补偿[2]。多环反馈控制方法[3]动态性能优越,设计过程简单且易于实现,控制器设计过程不依赖于精确的逆变器参数。传统的多环反馈控制在环路中使用的是普通PID调节器,普通的PID调节器只能对直流信号做到稳态时的无差调节,在多环瞬时值反馈环控制时,由于输出和给定的信号都是交流信号而产生稳态误差。系统在稳态精度方面存在缺陷。为了克服上述问题,本文提出了一种适用于单相和三相系统的含有交流PI调节器的多环反馈控制方法,它能消除静态误差,有效提高稳态精度,并可获得良好的瞬态性能。且与传统的多环反馈控制一样,易于设计和实现。
2 交流PI调节器
直接作用于交流信号,静止坐标下的交流PI调节器可以获得稳态的零误差,这在电力电子系统中还很少见,但是,在伺服控制理论中已经得到了很好的发展。它的基本原理就是把一个直流补偿网络转换为一个交流补偿网络[4~7],这样,在相同的带宽中它们就有相同的频率响应特性。
单相系统交流PI调节器的等效原理图如图1所示。在图1中,通过把误差信号转换为直流信号,再利用直流调节器来对直流信号进行控制,所以普通的PI调节器就可以保证对直流信号无静差跟踪。由图1可得[4]:

式中:*表示卷积;ω为角频率。

图1 单相系统交流PI调节器等效原理图Fig.1 AC PI regulator block of single phase
把图1的虚线框等效为一个交流PI调节器,则可用下式表示

式中:HAC(s)表示交流 PI调节器的传递函数。式(2)的时域表达式为

定义2个函数 f1(t),f2(t)

它们的Laplace变换形式为

式(1)可以分为两部分,分别用A和B来表示。

由式(1)、式(7)、式(8)可得

比较式(2)和式(9)得

如果

则

其伯德图如图2所示。

图2 交流PI调节器伯德图(KP=0.5,KI=1,ω=800π)Fig.2 Bode plot of AC PI regulator
从图2中可以看出,其幅频特性在基波频率处(也叫谐振频率)达到无穷大(由于仿真步长和截断误差的原因,其值为一有限值)。而在其它频率点处增益相对较小。
3 电压外环、电容电流内环双环系统分析
对于传统的三相系统,可以通过变换或直接简化为单相系统来考虑[8~10]。因此,为了分析的方便,下面将以单相系统为例来说明等效的交流PI调节器在逆变器中的应用。
图3为本文所采用的单相逆变器的拓扑结构图。其中Ud为直流母线电压,L,C分别为逆变器输出滤波电感和电容,r表示滤波电感等效串联电阻、死区效应等逆变器中各种阻尼因素的综合等效电阻。逆变器采用单极倍频调制方法,可达到2倍频工作效果,有利于减小输出滤波器的体积和重量。图4为其采取电压瞬时值外环加电容电流内环的逆变器控制框图。根据逆变器平均值模型[1,8],PWM逆变部分可简化为一个比例增益KPWM,Io代表负载电流,可以把它看作是系统的一个外部扰动输入量,这样处理的好处是既符合逆变器负载多种多样的实际情况,又可以建立一个形式简单且不依赖具体负载类型的逆变器数学模型。

图3 单相逆变器拓扑图Fig.3 The topology of single phase inverter

图4 采用电压外环、电容电流内环的单相逆变器控制框图Fig.4 Single phase control block of multi-loop control with inner capacitor current and outer voltage feedback
考察一下逆变器输出波形的控制问题。首先,逆变器波形控制系统是一个指令呈正弦规律变化的伺服系统,而不是一个恒值调节系统。至于系统的扰动即负载电流,当负载为线性时是按正弦规律变化的;当负载为非线性时则是按非正弦规律变化的,总之也不是恒值扰动。也就是说,对于线性负载,只需要一个基波频率处的交流PI控制器;而对于非线性负载,除了需要基波频率处的交流PI控制器外,系统需要抑制哪些谐波,还需要哪些谐波频率处的交流PI控制器。
考察系统的输入到输出的传递函数,由图4得它的开环传递函数与闭环传递函数分别为

在式(12)和式(13)中把KPWM和Gi′的乘积作为电流内环的增益Gi,取Gi=0.33。

当电压外环采用式(14)所示的交流PI(图5中用 PR 表示)控制器时 ,L=26 μ H,C=440 μ F,r=10 mΩ,ω=2π×400,Kp=8,K1=6 000,Ki=1 500,i=3,5,7时,这时外环开环、闭环传函的频域特性分别如图5a、图5b所示,图5中同时还给出了采用P控制器和PI控制器时的伯德图。从图5中可以看出采用PR控制器只是在谐振频率处对系统的频域特性有影响。开环特性中,在谐振频率点处的幅值增益近似无限大,因此系统对基波频率信号能达到零稳态误差,同时能够很好地补偿3,5,7次谐波;在其它频率处的幅频特性与采用P控制器时基本重合。积分控制最多能在低频段给系统增加一点开环增益,从而在逆变器输出频率(一般也还位于系统的低频段)上略微降低一点静差,但同时却带来显著的相位滞后,危及系统的稳定,可以说是得不偿失。

图5 系统伯德图Fig.5 Bode plots of sy stem
闭环特性中,谐振频率点处的幅值和相位都近似为零,这说明输出与输入之间没有幅值和相位误差,输出能够很好地跟踪输入。因为参考输入中无3,5,7次谐波,因此输出信号中的3,5,7次谐波也近似为零。
考察系统的输出阻抗,由图4得:

当外环采用比例控制器时,输出阻抗的频域特性如图6中的P线所示,其频域特性在400 Hz,1.2 kHz,2 kHz,2.8 kHz处的幅值分别是-34.2 dB,-24.1dB,-17.2dB,-15.2dB。当外环采用式(5)所示的PR控制时,输出阻抗的频域特性如图6中的PR所示。同样,除了基波和3,5,7次谐波频率处以外,PR和P线基本重合。其频域特性在400 Hz,1.2 kHz,2 kHz,2.8 kHz处的幅值分别是-135 dB,-116 dB,-107 dB,-102 dB,所以外环采用PR控制器时,系统的输出阻抗大大减小,可有效地抑制负载电流对输出电压的影响。

图6 输出阻抗频率特性图Fig.6 Frequency characteristic of output impedance
整个系统的闭环传递函数为

由式(16)可知,当Gv=∞(采用交流PI调节器在谐振频率处)时,等式右边的第一项系数等于1,第二项系数等于0。则式(16)变为

采用交流PI调节器后,系统能够实现对正弦指令信号的稳态无静差跟踪。即无幅值误差,又无相位误差。
对于三相系统,交流PI调节器同样可以应用,限于篇幅,将后续报道。
4 仿真研究
为了验证上述分析,对图3所示单相逆变器带线性、非线性负载,突加突卸负载进行仿真研究。仿真系统参数如表1所示。

表1 系统仿真参数表Tab.1 Simulation parameters of the sy stem
4.1 单相线性负载
负载为串联的阻感型负载,负载电阻1.0 Ω,负载电感315.7 μ H,功率因数为0.8。参考电压和输出电压波形如图7a所示,从图7a中可以看出,输出电压与参考电压之间基本上没有稳态幅值和相位误差,输出电压THD为2.4%,为了比较起见。图7b给出了电压外环采用P控制器时的仿真波形,从图7b中可以看到输出与参考之间有明显的幅值和相位误差。

图7 阻感负载时的电压波形Fig.7 Voltage waveforms with RL load
4.2 非线性负载
当负载为二极管整流型负载,整流器输出接LC滤波,滤波电感和电容分别为30 μ H 和1 800 μ F,整流器负载为2 Ω电阻,输出电压电流波形如图8a所示,负载电流THD为71.21%。输出电压谐波含量如图8b所示,输出电压 THD为2.61%,可以看出3,5,7次谐波都得到有效的抑制。输出电压在一个基波周期内即可达到稳定误差限制范围之内,系统具有良好的动态性能。

图8 非线性负载时交流PI控制下的输出电压、电流波形Fig.8 Voltage and current waveforms with AC PI Regulator under nonlinear load
突加突卸非线性负载的仿真波形如图9所示。从图9中可以看出,在0.02 s时,突加非线性负载,在0.05 s时,突卸非线性负载,输出电压几乎都没有变化。这说明系统具有很好的鲁棒性。
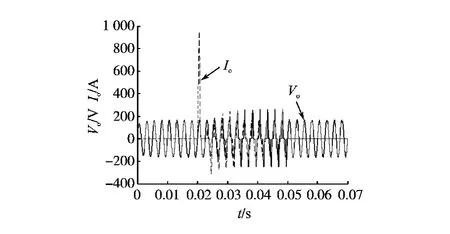
图9 突加突卸非线性负载时输出电压、电流波形Fig.9 Output voltage and current waveforms under step changes in nonlinear load
5 结论
本文对CVCF逆变电源的波形质量控制方法进行了研究,通过采用单极倍频调制技术,提高了等效开关频率,有助于改善输出电压的波形质量;针对传统的PI调节器会对交流输入信号产生静态误差,引用伺服控制系统中的直流调节器转换为交流调节器的理论,推导出一种新的交流PI调节器,该调节器能对交流输入信号达到无静差跟踪,并能获得良好的动态性能。理论分析和仿真结果表明,该方法是有效的。
[1]Zhang K,Kang Y,Xiong J,et al.Repetitive Waveform Co rrection Technique for CVCF-SPWM Inverter[C]∥IEEE PESC 2000 Galway,UK,2000:153-158.
[2]Cha H J,Kim S S,Kang M G.Real-time Digital Control of PWM Inverter with PI Compensator for Uninterruptible Power Supply[C]∥Proc.of 1990 PESC CA,USA,1990:170-176.
[3]Jung S L,Huang H S,Chang M Y.Digital Multiple-loop Control Technique for the PWM Inverters Used in Uninterruptible Power Supplies[C]∥IEEE-APEC 1997 Atlanta,USA,1997:706-712.
[4]Zmood D N,Holmes D G.Stationary F rame Current Regulation of PWM Inverters with Zero Steady-state Error[C]∥Proc.of PESC 1999.SC,USA,1999:1185-1190.
[5]Zmood D N,Holmes D G.Stationary F rame Current Regulation of PWM Inverters with Zero Steady-state Error[J].IEEE Trans.On PE,2003,18(3):814-821.
[6]Mattavelli P.Synchronous-frame Harmonic Control for High-performance AC Power Supplies[J].IEEE Trans.,2001,37(3):864-872.
[7]Zmood D N,Holmes D G,Bode G H.Frequency-domain Analysis of Three-phase Linear Current Regulators[J].IEEE T rans.,2006,21(4):601-610.
[8]Ryan M J,Brumsikle W E,Lorentz R D.Control Topology Options for Single-phase UPS Inverters[J].IEEE T rans.,1997,33(2):493-501.
[9]Li Y W,Vilathgamuwa D M,Loh P C.A Grid-interfacing Power Quality Compensator for Three-phase Three-wire Microgrid Applications[J].IEEE Trans.,2001,37(2):1021-1031.
[10]Borup U,Enjeti P N,Blaabjerg F.A New Space Vector Based Control Method for UPS Systems Powering Nonlinear and Unbalanced Loads[J].IEEE Trans.,2001,37(6):1864-1870.

