基于逆线性二次型的感应电动机的控制系统研究
姚舜才,潘宏侠
(中北大学 信息与通信工程学院,山西 太原 030051)
1 引言
由于感应电动机性能可靠,结构简单,因此在电力拖动系统中有广泛的应用。目前,很多感应电动机控制系统基本采用矢量控制的思想,即通过一定的坐标变换进行简化,然后在d-q系统中应用传统的PI调节器进行控制。然而,感应电动机是一个典型非线性系统,尽管将其进行坐标变换后仍然不能改变其非线性、强耦合的特点,因此其性能也在很大程度上难以提高。针对这一问题,本文提出了一种基于逆线性二次型(ILQ)的感应电动机控制系统的设计方案。首先,使用了在非线性系统理论中的状态反馈线性化方法,对感应电动机的状态方程进行反馈线性化;然后,使用ILQ设计方法,设计了感应电动机控制系统。实验结果表明,与传统的控制方法相比本文所提出的方法有较强的鲁棒性和有效性。
2 感应电动机状态方程的线性化
在d-q旋转坐标系中,取定转子电流、旋转角度以及角速度为状态向量;电压和转矩为控制向量,感应电动机的状态方程为[1]

式中:U为电机电压向量;i为电机电流向量;R为电机绕组的电阻向量;L为电机电感矩阵(含自感、互感);Ω为电机转子的旋转速度;θ为转子位置的电角度;Te为电机电磁转矩;Tl为负载转矩。
这是一个非线性系统,为了便于逆线性二次型控制规律的实现,可以将其进行反馈线性化处理,将交直轴电流按下式给定[2]:
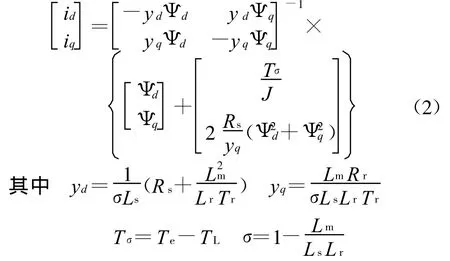
经反馈线性化处理后,电机的数学模型变化为状态空间的标准形式,即有:

实际上这也是一个分块矩阵的表达形式,具体表达形式可参见文献[2]。在设计控制系统的过程中,如果将电机转速与转子位置角度这两个状态变量忽略,便形成一个解耦的线性系统。这个系统的状态矩阵、控制矩阵以及输出矩阵分别为
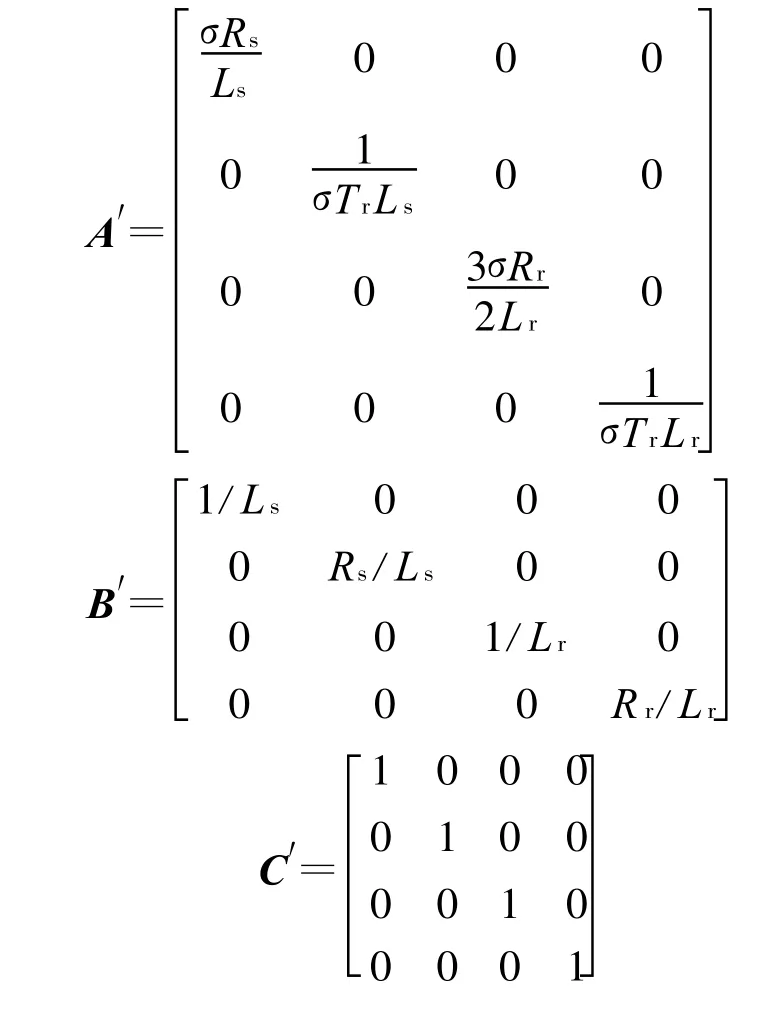
此系统中,系数矩阵A,B,C都是4×4的对角阵且都是非奇异矩阵,此时控制向量及控制方程选为

式中:Ωdqs为定子磁场同步速;Ωdqr为转差速度;vd,vq作为电压控制向量ud,uq的标称指示值。
3 逆二次型的感应电动机控制系统设计
要使用逆二次型的设计方法对一个系统进行设计,它要求系统的状态方程必须满足下面3个条件:1)系统式(4)必须是可控的,可观测的;2)系统的初始平衡点不是零点;3)系统式(4)是最小相位系统。在这3个条件中,条件1)和条件2)显然是满足的。下面证明第3个条件也是成立的[3]。具有积分环节的优化ILQ控制系统的结构如图1所示。

图1 优化ILQ控制系统的结构图Fig.1 The structure of ILQ optimal servo system
图1中,输出y直接反馈给给定值r,KI为积分增益放大器,KF为反馈增益放大器。∑=diag{σi},(i=1,2)为一对角阵,用来调整参数增益。此时,ILQ优化伺服系统的传递函数Gyr(s)有如下关系:

z为传递函数的零点,且对于系统式(3)有:
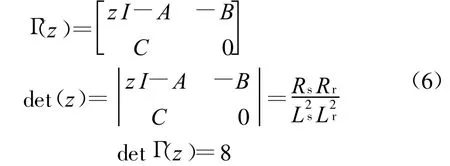
由此可知,该最小相位系统没有不稳定零点 。
图1所示的ILQ优化控制系统要求最佳增益,同时由系统是最小相位系统的条件可知,解耦矩阵也是非奇异的,并可写作:

di是相对阶。若令di的阶数为1,此时由于维数变化,则优化ILQ控制系统的稳定多项式为
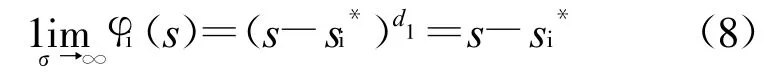
ILQ优化系统的目标传递函数即为

由式(7)~式(9),并结合系统的稳定多项式,可得解耦增益K为

结合图1所示,标准最佳积分增益与反馈增益为

要实现图1所示的ILQ优化控制系统,必须满足下面的3个充要条件[4]:

考虑到感应电动机转子电流分量为定子所决定,因此将独立状态变量减少两维。此时ILQ优化控制系统充要条件1)中的矩阵E可化为

由充要条件2),矩阵F可化为

充要条件3)可表示为

由此可得出:

所以优化控制系统的最优条件可写为
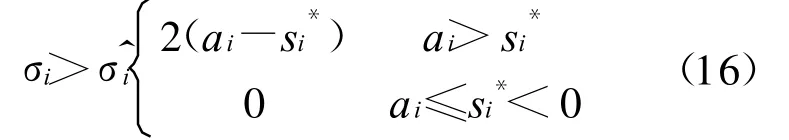
根据以上推导,可以得出如图1所示ILQ优化控制系统的传递函数为由此传递函数。可以得出优化系统的根轨迹图如图2所示。


图2 ILQ优化系统的根轨迹图Fig.2 Root locus of ILQ optimal system
图2a表示的是在特殊极点σ*i<ai处的根轨迹,实线部分满足最优条件式(16)中的最佳条件域,虚线表示满足另一个条件域。若r=实部应满足条件0<σi≤ai-2s*i-2r,虚部应满足 ai-2s*i-2r<σi<ai-2s*i+2r。图2b表示了当特征根在左半平面靠近虚轴时,系统解的实部又返回到ai-2s*i+2r≤σi,并沿着实轴趋于负无穷的过程[5]。
4 实验及结论
图3为三相感应电动机的ILQ优化控制系统结构图。该控制系统的组成部分包括:电压控制型PWM逆变器、感应电动机、测功机以及相关的控制设备。

图3 感应电动机的ILQ优化系统结构图Fig.3 The structure of ILQ optimal control system for induction motor
本系统通过PC机作为上位控制计算机,通过运动控制卡并经可编程模拟输入信号线与变频器连接。其中运动控制卡为研华PCI-1247,变频器采用爱默生EV3000-4T0037G,制动单元选用TDB-4C01-0150,输入电抗为TDL-4AO01-0075,具体的硬件连接框图如图4所示。
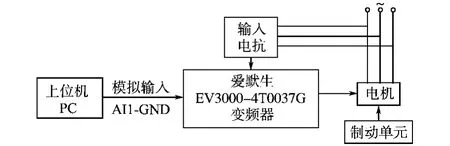
图4 感应电动机控制系统的硬件结构Fig.4 T he hardware structure of induction motor control
在上位计算机(PC)中,控制流程图见图5。

图5 感应电动机控制系统的软件结构Fig.5 The software structure of induction motor control
时间常数是IP电流控制系统的时间常数为[6]

经过适当调整,系统可达到ILQ优化的运行状态。图6为带有PI调节器的感应电动机矢量控制系统和所提出的ILQ优化控制系统对于给定信号的跟踪情况和电流变化的鲁棒性对比。图6中,带有PI调节器的感应电动机矢量控制系统在跟踪给定信号变化时,有20%的滞后;而本文所提出的ILQ优化控制系统跟踪给定信号变化时,其滞后仅有10%,与传统方法相比有了很大提高。此外,当给定信号发生突变时,则有:

经历一定时间后,电机电流将渐近收敛于给定值,若电机交、直轴电感在不超过±20%范围内变化,反馈将会抵消这部分影响[7]。这一点从跟踪给定信号的电流变化曲线上可以看出,这说明ILQ优化控制系统的鲁棒性与矢量控制系统相比也相应增强了。

图6 两种控制系统效果的对比Fig.6 Comparison of the two control system effect
[1]汤蕴缪,张奕黄,范瑜.交流电机瞬态分析[M].北京:机械工业出版社,2005.
[2]王勋先,韩曾晋.基于反馈线性化的感应电机2-自由度控制系统[J].清华大学学报(自然科学版),1999,39(9):243-249.
[3]Yoko Amano,Satoshi Ogasawara.Robust Current Control System of Synchronous Reluctance Motors U sing Inverse LQ Design Method[J].IAS,2005,23(5):745-750.
[4]Kimura H,Fujii T,Mori T.Robust Control[M].Corona.Publishing Co.,Ltd.1994.
[5]Takami H.An Optimal Current-control Desig n for Permanent M agnet Synchronous Motor by ILQ Design M ethod[J].Trans.CICE,2002,38(3):327-329.
[6]Qu Z H,Cloutier J R.A New Suboptimal Control Design for Cascaded Non-linear Sy stem[J].Optimal Control Applications&Methods,2002,23(6):303-328.
[7]梅生伟,申铁龙,刘康志.现代鲁棒控制理论与应用[M].北京:清华大学出版社,2004.

