天津电网小干扰稳定分析及控制

邓 斌，韩文茂，邓集祥

（1.天津电力公司调度中心，天津 300010；2.东北电力大学，吉林吉林 132012）

天津电网小干扰稳定分析及控制

邓 斌1，韩文茂1，邓集祥2

（1.天津电力公司调度中心，天津 300010；2.东北电力大学，吉林吉林 132012）

0 引言

在近几年我国将初步形成以三峡电网为中心的北部（东北、西北、华北和山东地区电网）、中部（华中、华东、川渝地区电网）和南部（广东、云南、贵州南方联合电网）三大区电网互联的全国统一电网[1-3]。目前，东北、华北已在联网运行，华北、华中、山东、川渝也在联网运行。这种大区互联带来了极为可观的经济效益，促进了电力工业的进一步发展；同时，如此规模庞大的电网形成之后，也将使小干扰稳定中的低频振荡问题更加突出[4-7]。例如东北电网中的伊敏电站，四川电网中的二滩电站，这种远距离大容量送电格局的存在，联网前低频振荡问题就较明显，联网后整个系统的小干扰稳定问题就更加引人注目[4，7]。实际上，实施大区电网互联至今，我国已发生多起低频振荡事故。如2001年以来四川二滩机组多次相对川渝和华中电网振荡；2003年云南电网500kV罗马线功率振荡；2005年蒙西电网相对华北主网振荡；都是属于小干扰稳定中的低频振荡问题。所以分析研究大区联网系统的低频振荡问题就成为近几年来中国电网的一个热门课题[8]。

分析低频振荡问题，在理论上有成熟的线性化特征分析法，但系统大了以后（超过1000节）计算系统特征根就成为特征分析方法应用的最大瓶颈[9]。对状态变量为几万以上的大区联网系统，即使要仅求出为数不多的系统弱阻尼低频振荡模式、区域间低频振荡模式也是相当困难的事。文献[4]采用对系统进行降阶简化的方法，完成了对规划中的大区联网系统的小干扰稳定分析；文献[5]采用追踪联网前系统主要低频振荡模式的方法，研究了山东电网低频振荡问题；文献[6]在2阶经典模型的基础上，求出了大区互联系统的主导低频振荡模式；文献[7]在保持系统潮流不变、网架结构不变、发电机总数不变的基础上采用特殊方法求出了与四川电网相关的系统主导低频振荡模式，并利用prony分析方法验证了所求出的这些主振模式的正确性。

本文使用中国电力科学研究院开发的综合稳定程序(PSASP)[10]，依据文献[7]的方法，针对华北、华中、山东、川渝联网系统（系统规模在两万阶以上），在国调330作业数据的基础上，完成了联网系统中天津电网低频振荡分析。对天津电网在联网系统中小干扰稳定水平，天津电网在整个联网系统低频振荡中的作用和地位做出了合理的评价。

1 线性化分析理论和方法

电力系统的动态过程可以用下列非线性状态方程来描述

式中，Ai为系统雅可比矩阵A的第i行，Hi为系统海森矩阵H的第i个子阵。因为研究的是 “低频振荡”问题，属于小干扰稳定范畴，所以分析系统动态特性和稳定性时，可采用线性化方法，把（2）式中的2阶及2阶以上项略掉。对x=Ax而言，其解为

这里，U为系统的右特征向量，符号{}N表示N阶对角阵，x0为状态向量的初值，λi为A阵的第i个特征根，也称为振荡模式，λi=αi± jΩi。如果对所有的特征根都有αi<0,那么系统在小扰动下将是渐进稳定的。

在n机系统中，应有n－1对低频振荡模式（机电振荡模式），其频率在0.2～2.5Hz范围内。为描述这些低频振荡模式的阻尼特性[11]，令

ζi为第i个模式的衰减阻尼比。如果ζi<0.03，则表明第i个低频振荡模式的阻尼很弱，必须采取相应措施来增强其阻尼，以保证系统的小干扰稳定。如果ζi>0.05，则表明其有较好的阻尼。对于弱阻尼、特别是区域间弱阻尼低频振荡模式可以通过线性相关因子(participation factor)[11]找出与其强相关的发电机，这些发电机就是系统的不稳根源。

特征分析理论是研究电力系统小干扰稳定的成熟理论，但如何克服特征分析方法中维数灾的问题也是这一方法在实际应用中的最大的难题。

2 prony分析方法

对电力系统2阶以至高阶解析解[12-13]的研究结果表明：在大干扰稳定中起主要作用的仍然是由系统雅克比矩阵求得的振荡模式，而在功角稳定中起主要作用的仍然还是这些振荡模式中的低频振荡模式。在扰动下系统的响应曲线也是由这些模式组成，而在功角曲线和功率响应曲线中，低频振荡模式应是其主要成分。这样就从理论上提供了直接从系统大、小扰动下的响应曲线来检测低频振荡模式，进而分析系统稳定性的一条途径。响应曲线可以来自仿真计算曲线也可以是系统实际测得的曲线，而仿真曲线的计算是不受系统规模限制的，所以只要有了从系统响应曲线中检测振荡模式的算法，就有了从另外一条途径分析大规模系统稳定性的方法。

Prony算法[14-16]采用指数函数的线性组合的方法来拟合等间隔采样数据，可以分析出信号中主要模式的频率、衰减因子、幅值和相位等，所以近年来被广泛用于从系统功角或功率曲线来检测低频振荡模式。为克服特征分析方法中维数灾的问题，通过检测系统响应曲线获得振荡模式提供了一种可行方法。但Prony方法是针对线性系统的，适合于分析系统非线性特性已不明显，或线性系统特性已恢复的情况，所以应用Prony方法分析曲线所含模式时应注意[10]：

1）取点数在100至500个点为宜。

在进行检测的过程中，应用物化探技术勘测矿物质的地质效果，应当结合相应矿产来有效检查地质效果，合理、科学的评估物化探技术的实际操作手段，这样才能为之后技术的合理应用奠定坚实的基础。在目前的地质环境当中，大多数矿物质通过以往的勘测手段往往很难进行监测，并且在对这一技术进行使用的过程中，需要结合地质结构的实际状况，这样才能得出合理的数据信息，并且结合这些数据信息来对勘测方案进行规划。对多样化的矿产勘查手段进行充分的应用，能够深入的分析矿产区域的矿物质特性、交通情况、地质状况等，这样才能物化探技术在矿产勘查工作当中得到有效的运用，从而实现最大化的地质效果。

2）曲线的起始时间应选择在故障结束以后，因为受故障影响，故障期间曲线的变化较大，非线性较强，这部分曲线不能反映系统自身的模态，还会影响prony分析的准确性。

3）取点间隔据实际情况而定，对于大系统，主要研究频率在0.1至2.5Hz之间的振荡模式，因此采用0.2s的取点间隔比较合适，但对于某些振荡频率较快的曲线，如果只采用0.2s的间隔，则曲线会很不光滑。

3 天津电网低频振荡分析

3.1 电网运行方式

计算系统为华北、华中、山东、川渝联网系统，东北电网简化为绥中等值两台机，西北电网简化为灵宝3台等值机。整个系统共有发电机892台，负荷大部分以动态负荷模拟，运行方式为国调下达的303作业，基本潮流为能够满足网内外三相故障暂稳要求的最大潮流。分析用程序采用PSASP，使用“逆迭代转Rayleigh商迭代法”依照文献[7]所提方法搜索低频振荡模式，并用prony算法作为互辅互成的辅助算法。

3.2 计算结果

计算得到与天津电网相关的低频振荡模式20多对，其结果分两部分给出：1）弱阻尼低频振荡模式；2）天津本地低频振荡模式。

1）弱阻尼低频振荡模式（见表1）。这个模式的频率为1.3Hz，机电回路相关比为30，显然是天津本地低频振荡模式。衰减阻尼比为0.01，阻尼很弱。图1给出了模式1的模态图，由图1模态图可以看出，振荡主要是在津军粮G2和津津三G6间进行的，两者振荡方向相反。京京三G6参与了振荡，但在与津军粮G2成90°的方向上（第3象限），作用影响不大。津军粮G2与这个模式的相关因子为0.49，而津津三G6仅为0.0045，相差甚远，起主导作用的是津军粮G2。

表1 弱阻及低频振荡模式

图1 模式1的模态图

2）天津本地低频振荡模式。作为例子,4个天津电网本地低频振荡模式列于表2。其中模式2的频率为1.23Hz，机电回路相关比为3，是天津本地低频振荡模式，衰减阻尼比为0.07，阻尼很强。参与振荡的发电机较多 （共有10多台发电机参与了振荡），除了津津三、津津一、津盘山这些天津电网的发电机外还有北京的京京一。由图2所列模态图可以看出，振荡是在津津三G6、津津三G5、津津一GG与京京一GY、京京一GX间进行的，振荡方向基本相反。与这个模式相关最强的依次是津津三G6、津津三G5、津津一GG、京京一GY、京京一GX、津津三G7、津津三G8、津津一GA、津盘山G4、津大港G3。津军粮G6、津军粮G7、津军粮G8也参与振荡，在津津三一侧。

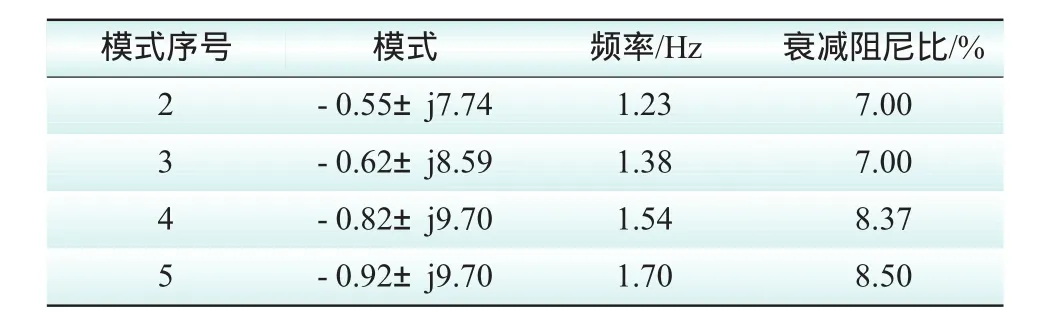
表2 天津本地低频振荡模式

图2 模式2的模态图

模式3，频率1.38Hz，机电回路相关比为8.8，衰减阻尼比0.07，阻尼很强。与这个模式相关最强的是津津一GG。由图3所列模态图可以看出，振荡是在津津一GG、GA和津津三G5、G6间进行的,两组机组振荡方向相反。

模式4，频率1.54Hz，机电回路相关比为7.1，衰减阻尼比0.0837，阻尼很强。振荡主要是在京高牌G4、G3和津津三G7、G8间进行的。

模式5，频率1.70Hz，机电回路相关比为10.4，衰减阻尼比0.085，阻尼很强。振荡主要是在津陈热G6和津军粮G5间进行的，振荡方向互为180°。

图3 模式3的模态图

3.3 prony验证

为验证上面计算结果的正确性，特别是模式1计算的正确性，在各种扰动下有关发电机的功角曲线上，用prony方法做了验证，prony拟合阶数为20阶。

1）在天津滨海一鄱阳路间1s时发生瞬时性三相短路故障，1.09s故障消失，在津军粮G2—津津三G6功角曲线上检测到其主要模式频率为1.299Hz，振幅为27.2，衰减阻尼比为0.99%。

2）在津军粮G2发电机出口变压器高压侧1s发生瞬时性三相短路故障，1.025s故障消失，在津军粮G2-津津三G6功角曲线上检测到其主要模式频率为1.30，振幅为19.2，衰减阻尼比为1.002%；在津军粮G2-京京三G6功角曲线上检测到其主要模式频率为1.30Hz，振幅为21.5，衰减阻尼比为1.01%。

3）当津军粮G2出力由50MW减少为45MW时，在津军粮G2发电机出口变压器高压侧1s发生瞬时性三相短路故障，1.025s故障消失，在津军粮G2—津津三G6功角曲线上检测到其主要模式频率为1.289Hz，振幅为10.2，衰减阻尼比为1.09%，阻尼有所改善。

对文中列出的其它模式，prony方法在各种扰动下有关发电机的功角曲线上检测到的结果与上面特征分析基本相同。

3.4 大区联网条件下天津电网小干扰稳定情况

在小干扰稳定分析中最应关注的应该是弱阻尼低频振荡模式，而在大区联网情况下最应关注的应该是频率在1.0Hz以下和多台发电机强相关的区域间低频振荡模式,如果这种区域间低频振荡模式的阻尼又很弱,那么对系统稳定的影响将更大。

由上一节的计算可知，在这个联网系统中，与天津电网相关的低频振荡模式中，模式1是与津军粮G2强相关的本地低频振荡模式，衰减阻尼比仅为0.01，阻尼很弱。但与其相对振荡，即处于振荡另一方的津津三G6和模式1的相关系数又相对很小（从图1模态图上也可以清楚看出），所以对系统小干扰稳定的影响不会太大。如果津津三G6和模式1的相关系数和津军粮G2相当，那么对系统的影响将加大。

所求出的低频振荡模式中，仅模式2和多台发电机强相关，其中包括天津电网以外的发电机，但模式2的频率在1.0Hz以上，充其量顶多也像上一节那样算作小区域间低频振荡模式。再者模式2的阻尼也很强，所以整体看来，天津电网对整个联网系统小干扰稳定不会起不利的作用。

3.5 模式1阻尼的改进

模式1是大区互联情况下天津电网阻尼很弱的一个本地低频振荡模式，与其强相关的发电机是津军粮G2。上一节在军粮G2出力由额定的50MW减少为45MW情况下计算的结果表明，降低津军粮G2出力使这个模式的阻尼有所增强，但改变不大。为增强模式1的阻尼，改进系统小干扰稳定性，可在津军粮G2上加装PSS。

在津军粮G2上加装PSS后，同样在津军粮G2发电机出口变压器高压侧1s发生瞬时性三相短路故障，1.025s故障消失时，在津军粮G2—津津三G6功角曲线上检测到其主要模式频率为1.306Hz，振幅为6.69，衰减阻尼比为4.28%，阻尼明显增强。而这个衰减阻尼比还是在津军粮G2发电机PSS参数没经优化套用其它发电机现成参数情况下得到的。也就是说，在津军粮G2上加装PSS的类型和参数是按照数据库中额定功率也是50MW且已装PSS的发电机的PSS的类型和参数设定的。如果加装在津军粮G2上PSS的参数经过优化，其效果还会更好。

4 结论

低频振荡问题是大区联网下系统稳定中的一个重要问题，如何计算分析大区联网下系统的低频振荡问题，或者说如何克服大规模系统低频振荡分析中的维数灾问题则是这一领域中的一个关键问题。本文在文献[7]的基础上，利用特征分析和prony检测相结合的方法完成了华北、华中、山东、川渝联网系统（系统规模在两万阶以上）中天津电网的低频振荡分析工作，求出了与天津电网相关的低频振荡模式，特别是弱阻尼低频振荡模式。并提出了增强系统阻尼，改进系统小干扰稳定的方法和措施。

[1]李琼林,刘会金,李智敏，等.异步联网HVDC系统中间谐波产生过程分析[J].南方电网技术，2008,2(2):49-53.

[2]刘本粹.西北电网外送暨宁东—山东±660kV高压直流联网示范工程浅议[J].电网与清洁能源,2010,26(1):9-13.

[3]张勇,陈建斌,余畅,等.联网后海南电网与主网严重故障下的相互影响及解列措施研究[J].南方电网技术，2009,3(5):50-53.

[4]朱方.大区电网互联对电力系统动态稳定性的影响[J].中国电机工程学报，2007，27（1）：1-7.

[5]王洪涛,刘玉田,雷鸣，等.电网互联对山东电网内部低频振荡模式的影响[J].中国电力,2004,37(6):12-15.

[6]黄莹，徐政，潘武略.基于PSS/E的华东电网低频振荡分析方法[J].电网技术,2005,29(23):11-17.

[7]邓集祥，贺建明，姚天亮，等.大区联网条件下四川电网低频振荡分析[J].电网技术，2008，32（17）：78-83.

[8]朱建国.水轮机及其调速系统对电力系统低频振荡的影响[J].电网与清洁能源,2008,24(6):62-64.

[9]王同文,管霖,张尧.基于知识发现技术的电网安全分析新思路[J].南方电网技术，2008,2(4):23-27.

[10]中国电力科学研究院.电力系统分析综合程序(PSASP6.2)用户手册[K].北京：中国电力科学研究院.

[11]倪以信，陈寿孙，孙宝霖.动态电力系统的理论和分析[M].北京：清华大学出版社，2002.

[12]Saha S,Fouad A A,liemann W.K.Stability Boundary Approximation of a Power System Using the Real Normal Form of Vector Fields[J].IEEE Trans,2005(12):797-802.

[13]邓集祥，陈武晖，纪静.基于正则形理论的电力系统2阶模态谐振的研究[J].中国电机工程学报，2006，26(24):5-11.

[14]芦晶晶,郭剑,田芳,等.基于prony方法的电力系统振荡模式分析及PSS参数设计.电网技术,2004,28（15）：31-44.

[15]邓集祥，涂进，陈武晖.大干扰下主导低频振荡模式的鉴别[J].电网技术，2007，31(7):36-41.

[16]彭波.南方电网低频振荡问题及PSS参数分析[J].南方电网技术，2009,3(4):31-35.

Analysis and Control of Small Disturbance Stability for Tianjin Power Grid

DENG Bin1，HAN Wen-mao1，DENG Ji-xiang2
（1.Dispatching Center,Tianjin Electric Power Corporation,Tianjing 300010,China；2.Northeast Electric Power University,Jilin 132012,Jilin Province，China）

Lowfrequencyoscillation is amajor problemin small disturbance stability, and it is a more critical one for an enlarged powersystem, especiallyin thecontextofinterconnection of regional grids. This paper, bymeans of combined method of the linearzed an alysis and pronyd etection,analyzes the low frequencyoscillation of Tianjin power grid in the context of interconnection of the regional grids, and find sout the low frequen cyoscillation mode, especially one fortheweak damping, which isrelated toTianjin grid. Methods and measures are proposed for enhancing the system damping and improving the smalldisturbancestabilityofthesystem.

large power grids interconnection;low frequency oscillationmode；characteristicanalysis；pronydetection;PSS

小干扰稳定中的一个中心和重要问题就是低频振荡问题，在系统扩大，特别是在大区联网下，这个问题更为突出。利用线性化分析和prony检测相结合的方法完成了大区联网条件下天津电网的低频振荡分析工作。求出了与天津电网相关的低频振荡模式，特别是弱阻尼低频振荡模式，并提出了增强系统阻尼，改进系统小干扰稳定的方法和措施。

大区联网；低频振荡模式；特征分析法；prony检测；PSS

1674-3814（2010）04-0011-05

TM937.3

A

2009-12-16。

邓 斌（1978—），男，硕士，工程师，从事电力调度工作。

（编辑 董小兵）