基于特征点能量优化的样条插值地形算法
原庆红, 韩 燮(中北大学 电子与计算机科学技术学院,山西太原 030051)
0 引言
由于战场地形仿真往往是大数据量的地形,其显示技术受到计算机硬件的限制,不能够实时地显示地形。如分辨率为90m的540×540km2的地形区域有36M个高程点,约有72M个三角形面元。我们发现高程数据点中一些关键性的特征点能表示曲面的形状,并且三次准均匀B样条曲线能自动保持曲面处的二阶连续,采用曲面插值特征点的方法能够准确拟合地形表面,这种方法计算量也较小。因此本文在对整个大地形的建模过程中,根据计算机的渲染能力,采用地形变分辨率技术,整体地形采用分辨率较低,对于重点关注地域使用三次准均匀B样条曲线插值特征点,生成高分辨率的地形曲面。
1 数字地形构建
1.1 数字高程模型
数字高程模型(Digital Elevation Mode简称DEM)是数字地形研究的主要对象。DEM是区域地形的数字表示,由一系列地面点的X,Y坐标及其相联系的高程,按一定的结构组织在一起表示实际地形特征的空间分布模型,DEM数据是国家基础地理信息系统数据中主要的一部分。本文使用ARC/INFO公司GRID格式的规则格网DEM数据。规则格网DEM是一种高程矩阵。它的优点是:结构简单,便于存储,有利于各种分析和计算。该格式包括2部分:第一部分为文件的信息头,如表1所示。第二部分是数据部分,即实际的高程值。自西向东按列记录DEM点的高程数据值,它的横坐标和纵坐标值可根据信息头中起始位置的横纵坐标和相邻网格的间隔值计算求得。其中格网点的高程值单位均为度。
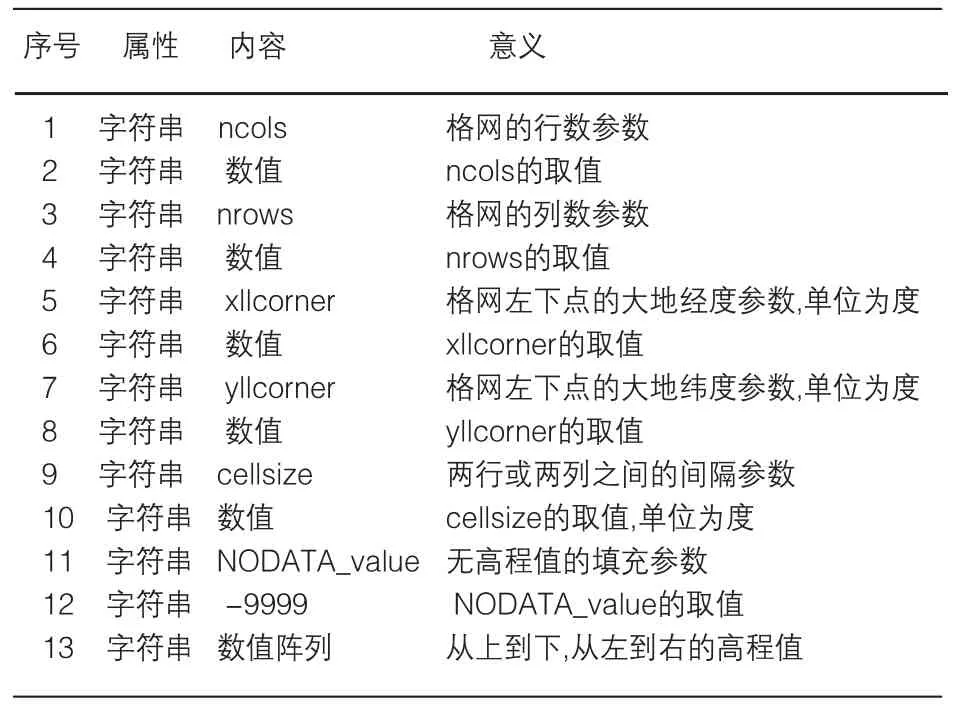
表1 ARC/INFO的GRID格式
1.2 三次准均匀B样条曲线
准均匀B样条曲线:其节点矢量中两端节点具有重复度k+1,即u0=u1=…=uk,un+1=un+2=…un+k+1,。定义域u∈[uk,un+1]内节点区间长度Δi=常数>0(i=k,k+1,…,n) ,所有内节点均匀分布具有重复度1。用三次准均匀B样条拟合规则格网的DEM数据,有以下优点:(1)第i段k次B样条曲线仅由V1,V2,…,Vk+1共k+l个顶点所控制,而与其他顶点无关。因此修改该段曲线,仅需修改相关的k+1个顶点。(2)该方法生成的曲线、曲面在边界处自动保持二阶连续性[2]。
2 基于特征点能量优化的B样条插值地形算法
曲线曲面拟合是数字高程模型重构中的一个重要步骤,目前地形重构的主要方法有:(1)bezier曲线插值法;(2)最小二乘法;(3)非均匀有理B样条法;(4)非均匀无理B样条法。方法(1)拟合的曲线变动一个控制点的位置,将影响到整个曲线的形状。方法(2)中最小二乘基函数不容易确定;方法(3)中权值难以确定,会使曲线的拟合效果很差[2]。本文在方法(4)的基础上,针对大地形中重点关注的兴趣区域,应用基于线性约束特征点能量优化的方法反算控制点。
2.1 算法过程
根据曲率信息从大量的数据点中提取特征点,若将这些特征点当作控制点生成的曲线只能逼近真实地形。为了更准确的表现曲线形状,不少学者探讨了使用最小二乘法反算控制点的方法[2],但在数据量较大时这个方法容易使拟合的曲线波动较大。我们采用了线性约束能量最小化方法反算控制点,该方法能更好地控制曲线的形状。在曲线形状细调方面,找出局部区间偏差较大的点,通过增加新特征点使生成的曲线更逼真。在二维平面上运用三次准均匀B样条曲线和线动成面原理生成地形图。
算法的总体流程图如图1所示。
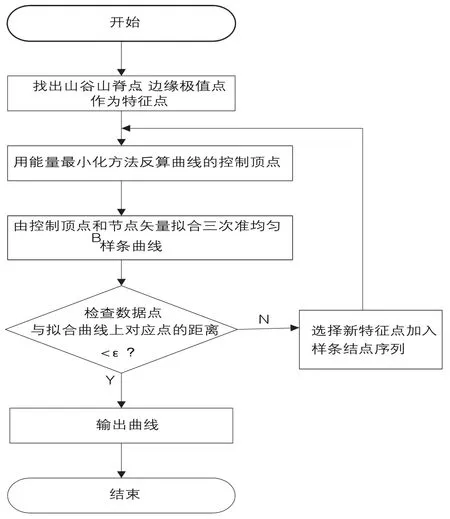
图1 基于特征点能量优化的大地形重构算法流程图
2.2 提取特征点
提取DEM数据特征点的目的是在减少模型数据点数情况下,尽量保持原始模型的形状。点的曲率在曲线形状描述方面提供了重要信息。在高程数据文件中根据数据点的曲率值,提取出曲率变化较大的点作为特征点。提取特征点的过程同时也去除了不重要的数据点。从大数据集中提取特征点进行曲线拟合,能使得在曲面地形较平坦的区域提取的特征点较少,反之在复杂的区域中提取的特征点较多。
根据边缘有序离散点的曲率值提取极值点[5]。对于规则格网边缘数据的每个点曲率定义为相邻3个点所构成三角形外接圆半径的倒数,如图2所示。即其中 是向量∅i之间的夹角,d是向量i的长度
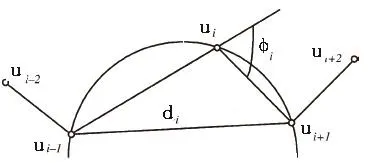
图2 边缘点的曲率值
2.3 用线性约束能量最小化方法反求控制点
物体重建的优化设计通常要求对控制点的权因子调节以便优化设计,最小二乘法是较实用的方法。将提取出的特征点作为节点,应用最小二乘法反算出控制点。然而在实际应用中,数据点和控制点的数目是经常变化的,当数据点和控制点数目十分接近时,最小化问题系统将变得十分不稳定且容易使拟合曲线波动增大。在这种情况下使用最小二乘方法就不太适宜。
故本文使用线性约束的能量最小化方法来反求控制点。曲线能量泛函函数:
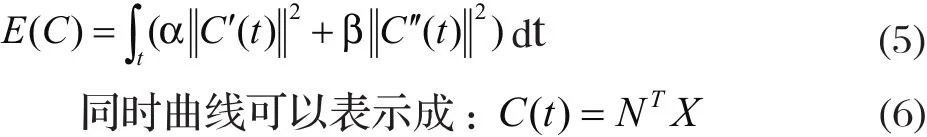
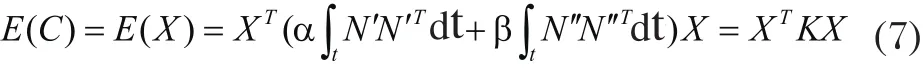
其中,非负系数 , 分别叫做伸缩系数、弯曲系数。一般取经验值: = 1 . 0 , = 0 . 2 ;N(k)表示B样条基函数的K阶导K称为曲线C(t)的劲度矩阵,由伸缩形式和弯曲形式的加权和表示为:
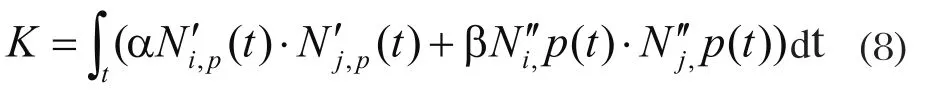
K是 (n+ 1 )*(n+1)的带状矩阵,带宽为2p−1。加入线性约束表达式为:AX=Q,其中Q是数据点向量,qi(i= 0 ,1,...m),x是存储曲线控制点的列向量,A是一个 (m+ 1 )*(n+1)的基函数数量矩阵。我们可以通过求最小二次函数E(X)的方法来求控制点向量X。即:。通过引入列矩阵,将最小化问题转化成求解下列线性系统的问题:由于线性方程是独立的,系统矩阵是对称、正定和非奇异的。因此[XV]T有唯一解。即得到B样条曲线的控制点向量X。由该方法得出的控制点数少于最小二乘法控制数点数,进而使拟合曲线分段数较少。
2.4 选择新特征点
使用三次准均匀B样条曲线逼近特征点拟合得到一条曲线C(t),找出数据点与该曲线上偏差最大的点pi,即,根据此点所在的局部曲线段寻找新特征点。误差最大点所在的曲线段至少包含3个点,如:Sm,n是特征点pm,pn所确定的曲线段,满足|m-n|>1。对偏差最大点所在的曲线段进行细分,在其中选择新的特征点。
Park等提出了考虑数据点的几何信息方法来划分曲线段,定义Sm,n上的形状指标:(9), 式(9)中0≤r≤1,Km,n是 曲 线Sm,n的 全 曲 率,,K0,m是 给 定 数据点的全曲率逼近,Lm,n表示曲线Sm,n的弦长,进行估计,L0,m表示给定数据点的弦长的逼近。r取经验值0.8最适宜,当数据点受噪声影响越大时,权重r就应该越小。运用式(9)求形状指标的方法,点pl将曲线段Sm,n分成两个曲线段Sm,l和Sl,n,使得这两分段的形状指标是最相似的,即在曲线段Sm,n上选取使得最小的点pl作为新的特征点,将该特征点加入到已有的特征点序列中。
3 实验结果
本实验对分辨率为90m的100行×100列数据进行了实验。构成的各曲面各片间是以位置、斜率与曲率连续为条件,故具有C2级连续性。图3是直接将高程数据点相连,即采样前的地形图。图4是采用基于特征点能量优化B样条插值的大地形重构反算控制点后,进行曲线拟合的三维效果图。
采用特征点能量优化的三次B样条曲线重构大地形,可以完成对大地形中重点关注区块的地形重构。当地形区域变化较剧烈时,该方法能更逼真地表现出实际地形的高低起伏状况。由三次B样条曲面的局部性,相邻四个顶点定义了一段曲线的形状,因此若改变某一个顶点的位置,其影响的仅仅是局部某段范围,因此可对起伏不平的局部地形进行调整,能保证得到较满意的地形精度。从图4可得出,经过特征点能量优化的三次B样条曲面,三角面片数多于图3,从而表现的地形图也更精确。

图3 采样地形

图4 三次准均匀B样条拟合地形
4 结束语
本文提出的基于特征点能量优化的样条插值地形算法,首先提取主特征点,用线性约束能量最小化方法反算出插值这些特征点的控制点,用三次准均匀B样条曲线逼近控制点,即得到插值主特征点的B样条曲线。弥补了直接使用双三次B样条拟合地形时数据量过大的问题;另外本文中使用了插值特征点的方法,而直接使用双三次B样条拟合地形是逼近所有数据点,所以运用该方法拟合的地形图更精确、更逼真。另外对拟合出的曲线根据误差界范围找出偏差较大点,通过增加新特征点的方法,更好地调整了曲线的形状。
通过测量仪器实测大地地面得到的高程数据,受测量仪器和测量方法的影响,数据点不可避免地存在误差,同时特征点的选取是通过曲率信息得到的,由于噪声影响曲率信息难以准确表达实际地形的变化情况。若对选取的特征点进行去噪,使得算法对噪声的敏感度降低,这样能更好的表达出地形实际信息。
[1]周红梅,王燕铭,刘志刚,等. 基于最少控制点的非均匀有理B样条曲线拟合[J].西安交通大学学报,2008(6):73-77.
[2]王栋,高成英,梁云,高月芳,等.基于等式约束最小二乘的B样条曲线拟合[J].中山大学学报,2008(7):15-18.
[3]洪莹,王继周,李昂.地形特征提取的一种简易算法[J].测绘科学,2009(6):125-127.
[4]张立民,邹容平,李一平,等.基于双三次B-样条插值的大地形重构[J].烟台大学学报:自然科学与工程版,2007(12):2093-2097.
[5]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社,2001.
[6]Hyungjun Park,Joo-Haeng Lee.B-spline cruve fitting based on adaptive curve Refinement using dominant point[J].Computer-Aided Design,2007(39):439-451.
[7]Hyungjun Park.Lofted B-spline surface interpolation by linearly constrained energy mimimizafion[J].Computer Aided Design(S0010-4485),2003,35(1):1261-1268.
[8]Wong Xuea,b,Min Sunc,Ainai Mac.On the reconstruction of three-dimensional complex geological objects using Delaunay triangulation[J].Computer Aided Design ,2004,26(20):1227–1234.
[9]Li W,Xu S,Zhao G,etal.Adaptive knot placement in B-spline curve approximation[J].Computer Aided Design ,2005,37(8):791-797.

