基于面元法的轴流泵叶轮敞水性能紊流数值分析
陈运杰,刘 超
(1.河海大学水利水电学院,江苏南京 210098;2.扬州大学江苏省水利动力工程重点实验室,江苏扬州 225009)
轴流泵由于其流量大、扬程低,在农田排灌、城市防洪排涝、跨流域调水等领域被广泛地使用.对轴流泵装置和轴流泵叶轮性能的研究一直受到相关研究人员的广泛关注[1-3].近年来,国内主要采用大型商用CFD软件对轴流泵性能进行研究[4-7].
面元法亦称边界元方法,目前已广泛应用于螺旋桨性能计算和空泡几何形状预报.同大型商用CFD软件相比,面元法数值分析容量小,运算速度快,且计算成本较低.轴流泵叶轮在工作原理、叶轮形式等方面与螺旋桨有相似之处,本文利用改进后的面元法程序对轴流泵叶轮的敞水性能进行预测,并和CFX-TASCflow软件的数值计算结果进行对比,以分析面元法程序是否能正确预测开敞式轴流叶轮的水动力性能.
1 面元法数值计算
面元法[8-9]基本思想是利用格林公式及拉普拉斯方程基本解的存在性,将描述不可压无黏无旋流动的二阶偏微分方程转化为流场中固体边界上的积分方程,从而将关于整个三维流场中速度场的求解转化为任意物面上(二维)未知奇点强度的求解.实际应用时,面元法的基本计算方法主要有2类,即基于速度场的计算方法和基于速度势的计算方法.本文主要采用基于速度势的面元法,即由来流条件事先确定物面上的源汇分布强度,就可以得到求解物面上偶极子强度(即扰动速度势)的积分方程.计算对象为Zm60型轴流式叶轮,该叶轮的进速系数为0.906,转速1450 r/min,直径150mm,毂径比0.46667,桨叶数为4.
1.1 方程离散
计算所用轴流式叶轮表面采用四边形双曲面元进行离散[10],计算时考虑了桨毂的影响,展向和弦向网格划分形式均采用双线性划分.轮毂的离散单元为螺旋分布.叶片尾涡从叶片随边逸出流向下游.叶轮表面和尾涡面的网格划分如图1所示.在边界的每个四边形面元上布置等强度的源和偶极子,应用Green定理,则边界问题的积分方程最终可离散为如下形式:
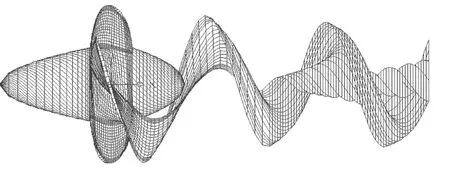
图1 Zm60型轴流式叶轮网格划分Fig.1 G rid generation of Zm60 axial-flow p ropeller
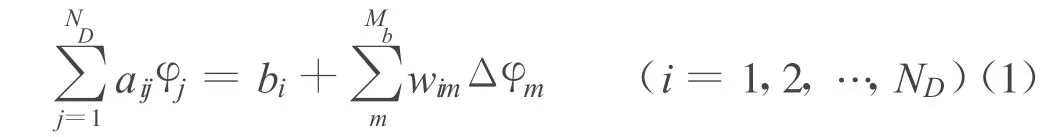
式中:aij——第j面元上单位强度的偶极子φj对第i控制点的影响系数;bi——源汇引起的在i控制点的总载荷;Mb——尾涡沿叶片展向面元数目;wim——第m尾涡条带上单位强度的偶极子对第i控制点的影响系数;Δφm——第m尾涡条带上的偶极子的强度;ND——叶片表面上及相应轮毂总面元数目.
1.2 敞水性能参数计算
计算时利用等压库塔条件来确定Δφm,即根据尾缘处上下表面面元控制点上压力相等的假定
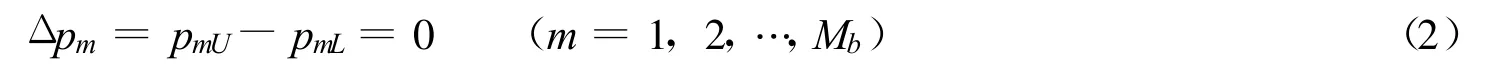
来确定Δφm.由式(1)和式(2)组成非线性方程组并进行迭代求解.如果经过数次迭代后,压力仍不收敛,更新雅可比矩阵,然后重新进行迭代计算.
根据Bernoulli方程,可求出叶片、轮毂表面的压力分布,并考虑黏性对推力及转矩的影响进而求得叶轮上的总推力T和总扭矩Q.
根据式(3)求得叶轮的推力系数KT和扭矩系数KQ.
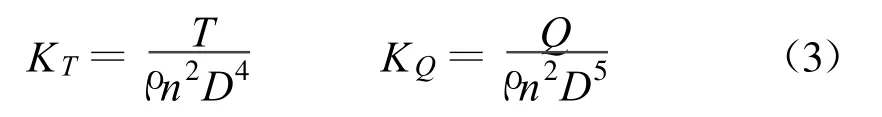
式中:ρ——流体密度;n——叶轮转速;D ——叶轮直径.
叶轮的推力系数和扭矩系数计算结果见表1,其中J为进速系数.
1.3 诱导速度计算
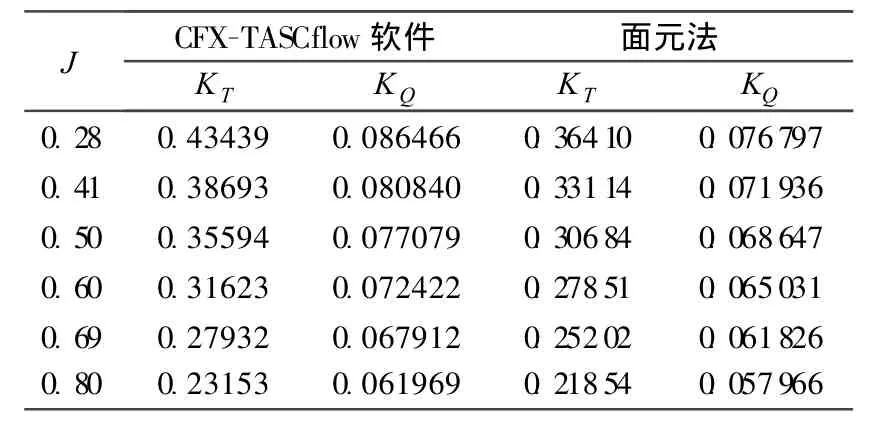
表1 Zm60型轴流泵叶轮敞水性能参数计算结果Table 1 Calcu lated results of performance of Zm60 axial-flow propeller
计算Zm60型叶轮在开敞工况的诱导速度时,尾涡模型采用收缩的尾涡模型,J=0.69,即取v=5.0m/s的工况进行计算.由诱导速度矢量图(图3)可知,水流从叶轮出来之后,形成较强的射流,靠近叶轮的部分有明显的收缩,而在远尾流区存在一定的扩散,如图2所示.图3所示叶轮后水流的环量较大,水流的圆周方向的速度较大.从图3可以清楚地看出轴流式叶轮出口处梢涡的存在(图中箭头所指处)及其周围的速度矢量分布.
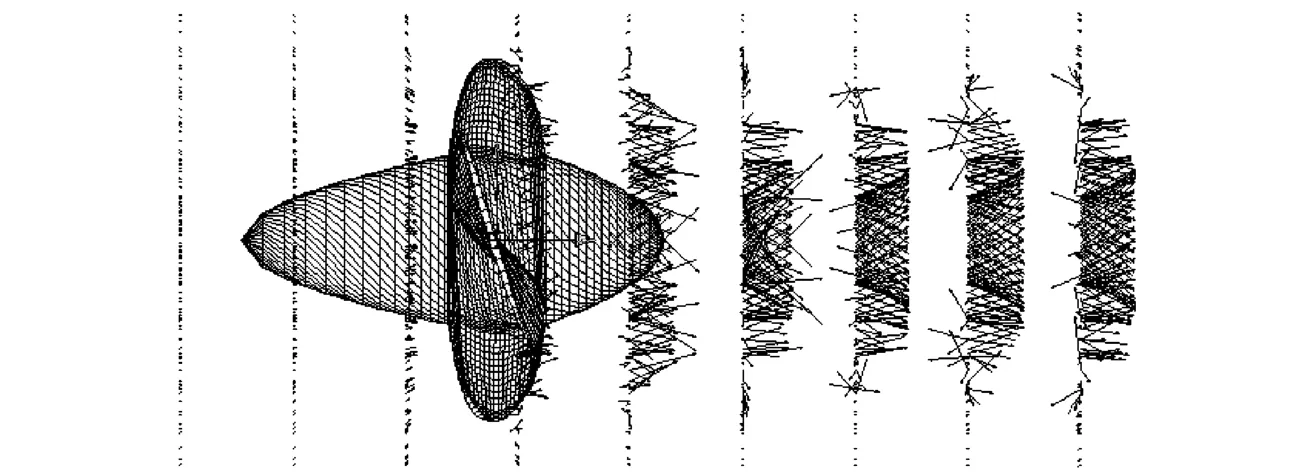
图2 Zm60型叶轮敞水诱导速度Fig.2 Vectors of open induced velocity of Zm60 axia l-flow p ropeller
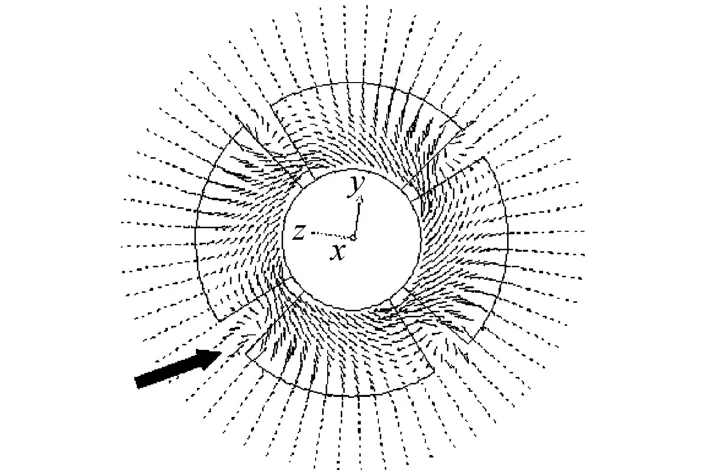
图3 Zm60型叶轮后截面诱导速度矢量分布Fig.3 Vectors of induced velocity of tail section of Zm60 axial-flow p ropeller
2 CFX-TASCflow数值模拟
采用CFX-TASCflow软件对Zm60型轴流泵叶轮在足够大的区域中的敞水性能进行数值模拟.计算采用的叶轮直径为300mm,轮毂比为0.4667,并建立一个直径为800mm、高度为1200mm的圆柱形水池作为叶轮运行时的区域边界来模拟叶轮的敞水工况,进而求解整个区域内的速度场、叶片表面的压力场和叶轮的外特性.
2.1 网格剖分
轴流叶轮模型以z轴为旋转轴,由编制的程序精确给出水池、叶片和轮毂3个实体的直角坐标数据文件:水池曲线(shroud)、叶片线型曲线(profile)和轮毂曲线(hub).采用CFX-TurboGrid软件进行实体造型和网格划分,网格质量可由CFX-TASCflow软件检查.整个网格正交性最大角度为158.1°,最小角度为22.4°.网格满足20°~160°之间正交性要求.整个计算实体网格剖分如图4所示.

图4 计算区域网格Fig.4 G rid generation of computational domain
2.2 边界条件及基本参数设置
计算时,外壳、叶轮及轮毂均采用无滑移固壁边界条件,即壁面速度为0.进口采用等压力分布边界条件,出口给出流速均匀分布的边界条件,并设定流体的周期性边界条件.在额定转速 n=1450 r/min下进行不同工况下的数值计算,解算器时间步长设为0.005,最大迭代次数采用1500,前后计算结果残差精度设为1.0×10-5.
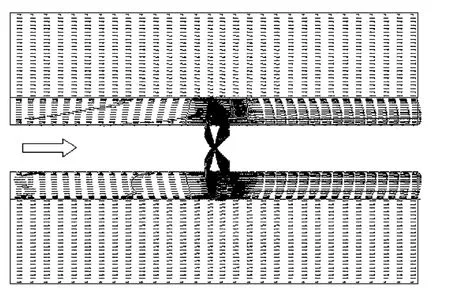
图5 J=0.69时相对流速矢量分布Fig.5 Vector distribution of relative velocity at J=0.69
2.3 计算结果及后处理
计算得到几种不同工况下的叶轮扭矩和推力以及J=0.69时区域内的流速矢量分布,为了便于分析比较,对计算结果进行后处理,使其在特定区域显示出来,如图5所示.根据式(3)求得了叶轮的推力系数和扭矩系数,计算结果见表1.叶片各剖面处的压力分布见图6(图中Cp表示压力系数,x/c表示控制点在弦长方向的位置,r/R表示毂径比).
3 计算结果分析
面元法和CFX-TASCflow软件的计算结果见表1.比较表1和文献[7]中表3的试验结果可知,面元法计算所得的扭矩系数和推力系数均比CFX-TASCflow软件的计算值和试验值稍小,但总体趋势还比较一致.计算值偏小的原因主要是轴流式叶轮的叶宽较大,叶梢处的环量分布与螺旋桨的有所不同,进速系数较小时,对程序预测结果精度有一定的影响.
由图6可知,面元法计算的压力在叶片上表面的进口和出口处较大,在中间表面压力分布的变化比较平缓,在叶片中部有2个较为明显的高压区.从图6还可以看出,在下表面靠近叶片梢部有明显的低压区,但CFX-TASCflow软件的计算结果,在叶梢部位靠近出口处,叶片背面的低压区更加明显,叶梢的压差较大,主要是因为计算时,考虑黏性的作用所致.面元法诱导速度的计算结果和CFX-TASCflow软件的诱导速度计算结果相比,分布和变化趋势比较一致.
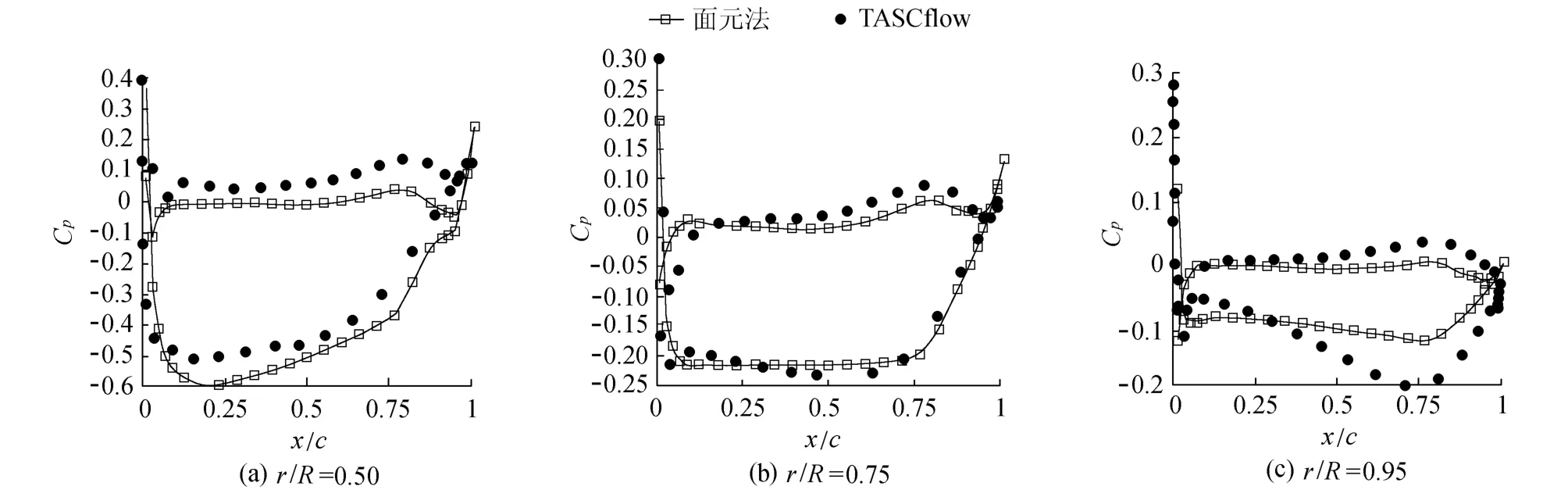
图6 表面压力分布比较Fig.6 Comparison of surface p ressure distribution
4 结 语
本文用面元法对Zm60型轴流泵叶轮的敞水性能,包括速度场、叶片表面的压力和叶轮的外特性进行了预测,并利用CFX-TASCflow软件进行数值模拟验证.通过对二者计算结果以及类似试验结果的对比可以看出,面元法计算所得的扭矩系数和推力系数均比CFX-TASCflow软件的计算值稍小,但总体变化趋势比较一致.由于目前此类三维流场测定有一定的困难,相关研究有待深入.总之,面元法能较好地预测轴流泵叶轮的敞水动力性能,诱导速度的计算也较为准确,压力分布比较符合实际,数值计算结果的准确性也得到了CFXTASCflow软件计算结果和类似试验结果的初步验证,在计算精度方面有待于进一步改善.
[1]成立,刘超.低扬程泵装置流动特性及水力性能研究进展[J].水利水电科技进展,2008,28(4):85-88.(CHENG Li,LIU Chao.Advances in research on flow characteristics and hydraulic performances of low lift head pumping station[J].Advances in Science and Technology of Water Resources,2008,28(4):85-88.(in Chinese))
[2]蒋小欣,王玲玲,李龙.数值模拟及可视化技术在旋转水力机械设计中的应用[J].河海大学学报:自然科学版,2006,34(4):414-417.(JIANG Xiao-xin,WANG Ling-ling,LI Long.Application of numerical simulation and VISC technique to rotary hydraulic machinery design[J].Journal of Hohai University:Natural Sciences,2006,34(4):414-417.(in Chinese))
[3]成立,刘超,汤方平,等.基于RNG紊流模型的立式轴流泵站三维流动数值模拟及性能预测[J].机械工程学报,2009,45(3):252-257.(CHENG Li,LIU Chao,TANG Fang-ping,et al.3D numerical simulation and performance predication of vertical axial flow pumping station by RNG turbulent model[J].Chinese Journal of Mechanical Engineering,2009,45(3):252-257.(in Chinese))
[4]施法佳,陈红勋.轴流泵内部流动数值模拟中湍流模式可用性的研究[J].上海大学学报:自然科学版,2006,12(3):273-277.(SH I Fa-jia;CHEN Hong-xun.Applicability of turbulent models in simulation of internal flow within axial flow pump[J].Journal of Shanghai University:Natural Science Edition,2006,12(3):273-277.(in Chinese))
[5]汤方平,王国强,刘超,等.高比转速轴流泵水力模型设计与紊流数值分析[J].机械工程学报,2005,41(1):119-123.(TANG Fang-ping,WANG Guo-qiang,LIU Chao,et al.Design and numerical analysis on an axial-flow model pump with high specific speed[J].Chinese Journal of Mechanical Engineering,2005,41(1):119-123.(in Chinese))
[6]李龙,王泽.轴流泵内部流动的数值模拟研究[J].流体机械,2007,35(4):16-18.(LI Long,WANG Ze.Numerical simulation of internal flow in axial pump[J].Fluid Machinery,2007,35(4):16-18.(in Chinese))
[7]黄欢明,高红,杜朝辉.轴流泵叶轮内部流动的数值模拟与实验[J].上海交通大学学报,2009,43(1):124-128.(HUANG Huan-m ing,GAO Hong,DU Zhao-hui.Numerical simulation and experimental study on flow field in an axial flow pump[J].Journal of Shanghai Jiaotong University,2009,43(1):124-128.(in Chinese))
[8]曹沛民.面元法预估螺旋桨性能[D].上海:上海交通大学,1992.
[9]陈运杰,刘超,汤方平,等.面元法预测在搅拌设备中轴流推进式搅拌器的水动力性能[J].高校化学工程学报,2008,22(6):1071-1075.(CHEN Yun-jie,LIU Chao,TANG Fang-ping,et al.Using surface panel method to predict the performance of the axialflow propeller type stieer working in a stirred tank[J].Journal of Chemical Engineering of Chinese Universities,2008,22(6):1071-1075.(in Chinese))
[10]NEWMAN J N.Distribution of source and normal dipoles over a quadrilateral panel[J].Journal of Engineering Mathematics,1986,20(2):113-126.

