大型风电场风机最优布置规律研究

王 丰,刘德有,曾利华,陈守伦,陈星莺

(1.河海大学水利水电学院,江苏 南京 210098;2.河海大学水资源高效利用与工程安全国家工程研究中心,江苏南京 210098)

风电场风机优化布置是风电场规划中的关键环节,其布置方案的优劣直接影响风电场的发电量以及风电场的经济性水平.在风电场区域边界以及该区域风资源确定的情况下,如风机布置数量太少,将会降低该区域风资源的利用率;但如风机布置数量太多、风机间距太小,则会由于风机尾流的影响而降低各单台风机的发电效益,从而降低整个风电场开发的经济性[1-3].因此,考虑风机布置数量在内的风机最优布置方案是风电场规划设计和开发过程中需要深入研究的重要课题.

在最初的研究中,风电场风机优化布置理论基本属于经验性结论,布置方式也基本为规则性的行列布置.如Patel[4]提出:风机布置的最优距离为在盛行风向上风机间隔8D0～12D 0(D 0为风轮直径),在垂直于盛行风向上风机间隔1.5D0～3D0.而王承煦等[5]指出:在盛行风向上要求风机间隔5D0～9D0,在垂直于盛行风向上要求风机间隔3D0～5D0.这些基于经验判断给出的风机布置间隔距离,在一定程度和特定阶段指导了风电场风机优化布置的探索研究和工程应用.Ammara等[6]曾据此构建了一个风电场风机布置方案,在保证相同发电量的同时,能够有效地减少风力发电机组的总占用土地面积.

实际上,不同风电场和风机类型的风机最优间隔距离是不相同的,上述经验成果只能在一定条件范围内作为风机优化布置设计的参考.为此,许多学者针对不同风况、不同区域边界的特定风电场进行了风机最优布置的更精确的计算研究.Mosetti等[7]首先提出了基于遗传算法的风机优化布置计算方法,把风电场总投资成本、发电效益作为优化变量,用两者的比值作为目标参数,评价不同风机布置方案优劣.该计算方法采用穷举法对不同风机布置方案进行经济比较,最终确定相对优化的风机布置方案,摆脱了风机经验布置间距的限制,可以获得更科学、合理的结果.Grady等[8]在Mosetti等[7]研究的基础上,利用遗传算法研究了风机优化布置问题,并结合理论分析,对风机优化布置形式进行了计算分析和校核,得到了更好的结果.Marmidis等[9]采用Monte-Carlo方法对风电场风机优化布置问题进行了研究,提出了研究该问题的新思路和新方法.

Mosetti等[7-9]的研究虽提出了若干创新性的计算方法和模型,研究成果也为风电场风机优化布置的研究和实际工程设计提供了重要的理论基础,但其中所采用的风机优化布置计算模型还不完善,更未对风电场风机最优布置的一般性规律进行系统的探讨分析和论证研究.

本文以风电场效益最大化为目标,在已有研究成果的基础上,采用一维非线性尾流扩张模型、基于动能衰减原理的尾流叠加模型、协调发电量与成本的风电场效益评价模型、考虑不同风机台数的发电量与成本之比的增量装机评价模型以及遗传算法[10]进行优化计算求解,研究了单风向风况和各典型风况下的风电场风机最优布置的一般性规律以及有关因素的影响关系.

1 单一风向风况下的风机最优布置规律

单一风向风况下的风机最优布置规律是复杂风况下风机最优布置规律的研究基础.因此,本文首先从风机最优布置间距、风速对风机最优布置间距的影响以及复杂边界风电场的风机最优布置规律等方面入手研究单一风向风况下的风机最优布置规律.

1.1 风机的最优布置间距

风机布置间距(中心点间距)包括垂直于盛行风方向的横向间距和盛行风方向的纵向间距.前人基于经验的研究结论是:风机的最小横向间距范围为2D0～5D0,最小纵向间距范围为5D0～12D0[4-5].实际上,风电场风机的横向、纵向间距应该按“在盛行风向上,上游风机尾流对下游其他风机出力无影响或影响很小”的原则确定.即对于不同的风电场,其最优风机间距是不同的,应根据风场区域形状及尺寸、风机类型等因素经综合优化设计计算后确定.但目前常用的上述风机间距取值范围所依据的主要是半经验性的风机优化布置数学模型,特别是其风机尾流模型存在较大的简化误差,故不能满足当今大型风电场的风机优化布置设计需要.

对于风电场区域无限制的情况,风机的最优纵向间距可按“上游风机尾流风速恢复至90%”的原则确定.即确定风机的最优纵向间距首先应研究确定风机尾流风速的变化规律.由于采用一维非线性尾流模型计算时,风机的轴向推力系数对风机尾流风速影响最大,其他参数如地表粗糙度、风机轮毂安装高程等影响较小,而由文献[11]可知,设计良好的叶片在其运行范围内大部分轴向诱导系数值一般为0.33左右,则可估算得到相应的推力系数为0.88左右,因此,可采用推力系数0.88求得对应的风机尾流风速与风机下游距离的关系曲线,如图1(a)所示.图中U0为风机上游风速,x为风机后沿轴向的距离.计算分析结果表明,该关系曲线受风轮直径D0的影响很小.由图1(a)可知,风机的最优纵向间距约为15D0.当风机采用排列状方式布置时,设首排风机出力为对应风电场自由风速下的最大出力,则在单一风向下不考虑横向风机之间的尾流影响和风机轴向推力系数的变化时,第2排风机的相对出力为72.9%,第3排风机的相对出力为53.1%.以此类推可知,当风场布置3排或3排以上风机时,后排风机出力受前排风机的影响很大,因此后排风机的纵向间距应适当增大.

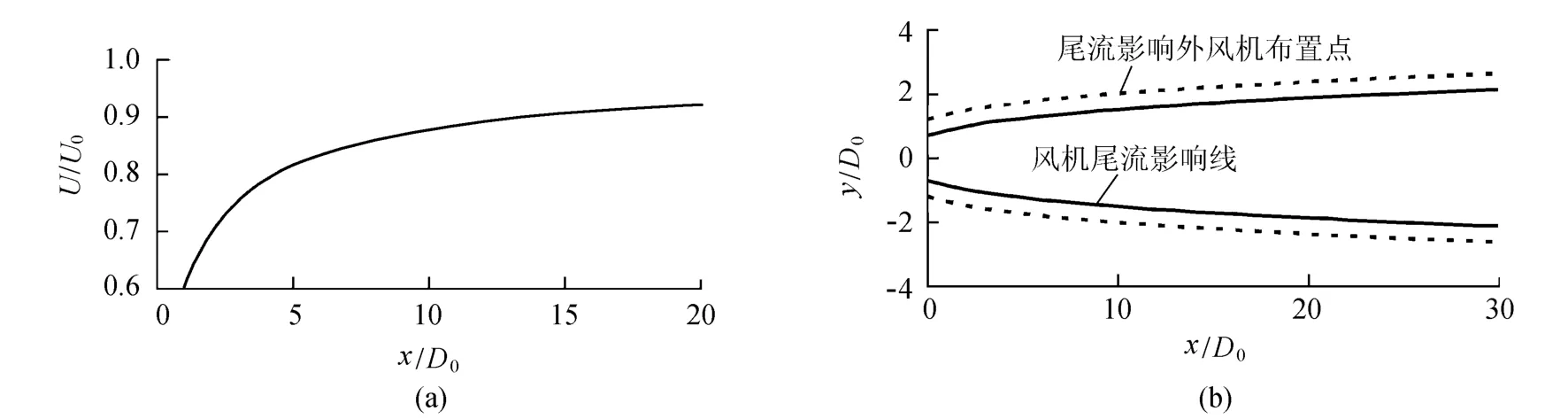
图1 风机尾流风速 U及尾流影响直径y的变化曲线Fig.1 Variation of relativewake flow and wakediameter of wind turbines

关于风机的最优横向间距,可按“上游风机尾流对其他列的风机出力无影响或影响很小”的原则选取.即确定风机的最优横向间距首先应研究确定风机尾流影响区域的变化规律,如图1(b)所示.由图1(b)可知,风机尾流影响范围(即影响区域直径)随着下游距离的增加而增加.当风场布置2排风机时,风机最小横向间距应为2.5D0;风场布置3排风机时,风机最小横向间距应为3D 0;随着风机布置排数的增多,风机的最小横向间距也应适当增大.

对于风电场区域确定的情况,受风场尺寸以及风电场开发经济性等因素的限制,风机最优布置间距一般需根据风场具体情况适当调整.例如,设某风电场尺寸为2000m×2000m,风机轮毂中心高程H0=60m,转轮直径D0=40m,推力系数CT=0.88,地面平均粗糙度 Z0=0.3m,风机额定风速13m/s,风机功率曲线按P=0.3ui3描述,ui为第i台风机的工作风速;风电场自由风速恒定为12m/s,0°方向来风,网格按照迎风方向划分为15×15,则风电场风机最优布置计算结果如图2所示,其风机出力、成本及适应值曲线如图3所示.

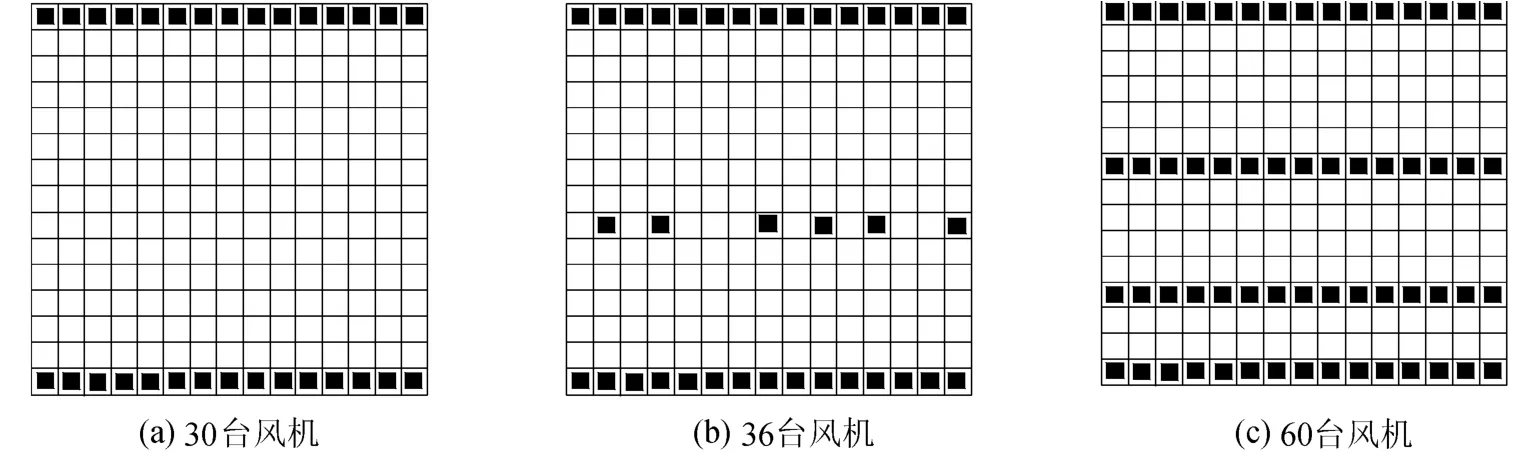
图2 风机布置方案Fig.2 Optimal configuration of wind turbines

从上述计算结果可以看出:对于单一风向风况的风电场,风机最优布置方式可为并行排状形式,风机最优排数可由风电场风机适应值曲线决定;随着风机数量的增加,对应最优布置方案的适应值参数随之改变,其总体趋势为先减小后增大,均存在一个极小值.对于上述算例,当风机布置少于3排时,其适应值较大,经济性较差;当风机布置为3排时,即风机数量为30～45台时,其适应值较小且变化不大,此时的风机最小纵向间距约为20D0;当风机布置为4排时,其适应值迅速增大,即风电场的经济性明显降低,此时的风机最小纵向间距约为10D 0.

对于上述算例,当其他参数不变时,改变该风电场区域沿盛行风方向上的纵向尺寸,可以计算得到其风机最优布置排数等参数,如表1所示.由表1可见:当风电场沿盛行风方向上的尺寸较小时(小于20D0),沿盛行风方向上应布置1～2排风机,风机的纵向间距在允许范围内应取最大值,而横向间距应为2D0～3D0;当风电场沿盛行风方向上的尺寸较大时(＞20D0),沿盛行风方向上可考虑布置3排或更多排风机,此时,风机的最优纵向间距为15D0～20D0,最优横向间距为3D0～5D0.

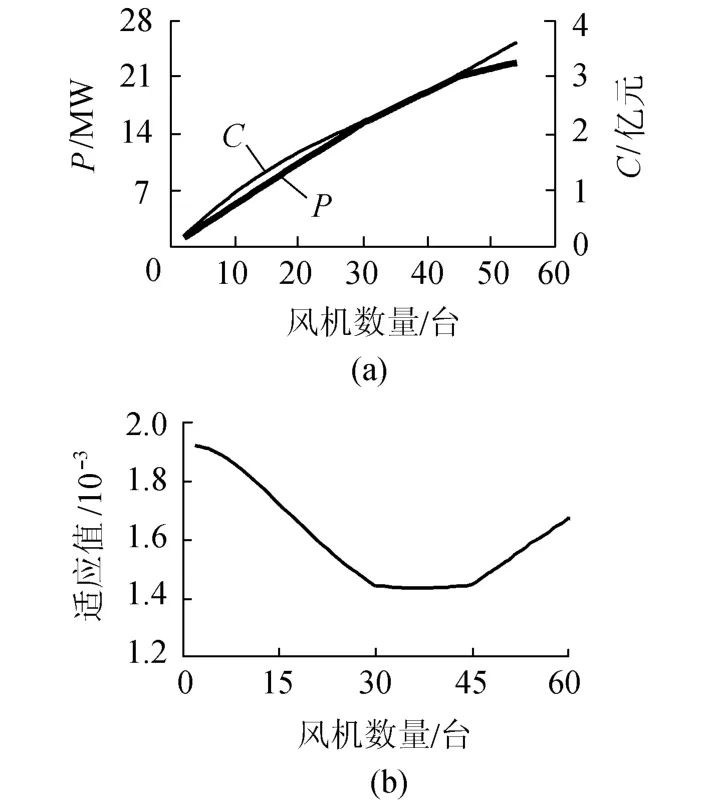
图3 风机总出力 P、成本 C及适应值曲线Fig.3 Output power,cost and fitness of wind turbines

表1 风机最优布置排数计算结果Table 1 Calculated results of optimal placement rows of wind turbines

1.2 风速对风机最优布置间距的影响

风电场自由风速变化时,风机的出力及尾流风速随之变化,风机最优布置也可能发生改变.对于区域无限制的风场,其最优布置间距根据尾流风速恢复系数确定,与风速大小无关;对于区域确定的风场,在风机排数一定的情况下,风速大小对风机最优布置间距可能存在一定的影响.

假设沿盛行风方向上,风场中分别布置3台、4台风机,如图4所示,并设图4(a)中的L1+L2=2000m,图4(b)中的L1+L2+L3=3000m,其余参数同前述算例.

在风机台数一定的情况下,以风机总出力最大为目标,把自由风速U1作为变量,经优化设计计算可得到风机布置位置以及风场风机总出力,计算结果如图5所示.

由图5可见,当沿盛行风方向上布置3台、4台风机时,其最优布置位置在一定的风速范围内是不变的.最优布置位置的突变条件是:随着自由风速的增大,中间风机出力增大至额定出力时,为满足风电场风机总出力最大,中间风机最优位置会逐渐向上游风机靠近;当风场自由风速足够大、风机均达到额定出力时,风机的最优布置位置会出现多值的优化计算结果.

图4 风机布置Fig.4 Placement of wind turbines

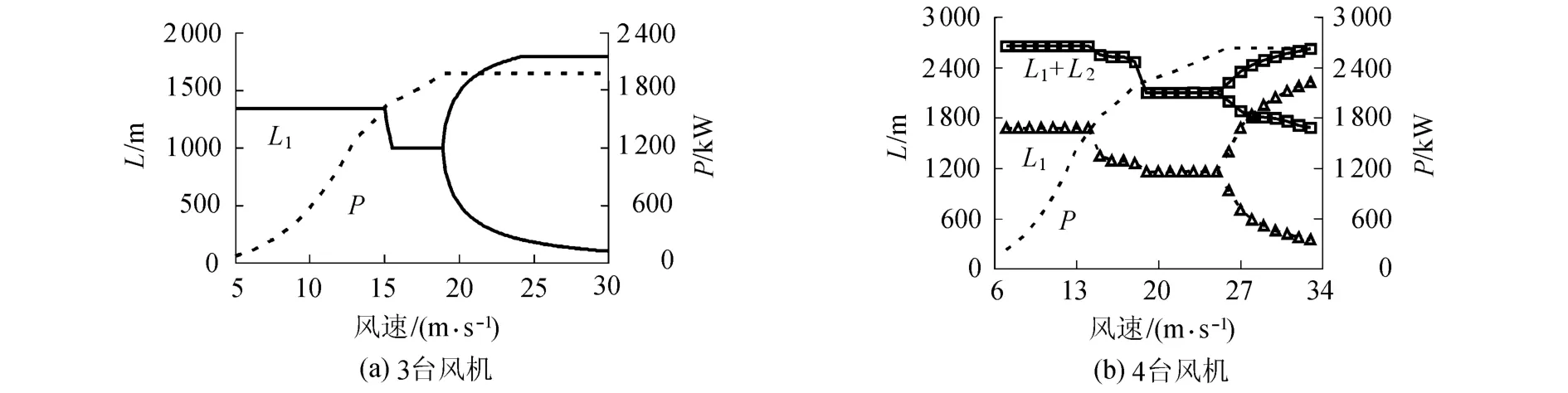
图5 不同上游风速下风机最优布置间距L与风机总出力P曲线Fig.5 Relationship between optimal spacing of wind turbines and output power under different upstream wind speeds

一般来说,由于风机年利用小时数相对较低,风场自由风速大多是在额定风速附近或小于额定风速.因此,在风电场风机优化布置时,只需参照图5中的第1段直线即可.也就是说,在风电场风机最优布置计算时一般不需考虑风速大小变化的影响.

1.3 复杂边界风电场的风机最优布置规律

风电场的开发可能由于某些因素限制,如用地限制、地形限制以及建筑物限制等,使得实际风电场的区域边界形状各不相同,这对风机最优布置方案也会有一定的影响.除上述方形风场外,对于梯形、圆形以及不规则形状的风电场,其风机优化布置的计算结果如图6所示.其中,对于不同形状的风电场,本文通过在风场内限制某些区域不允许布置风机的方式实现,在图6中,不允许布置风机的网格点以“×”号表示.

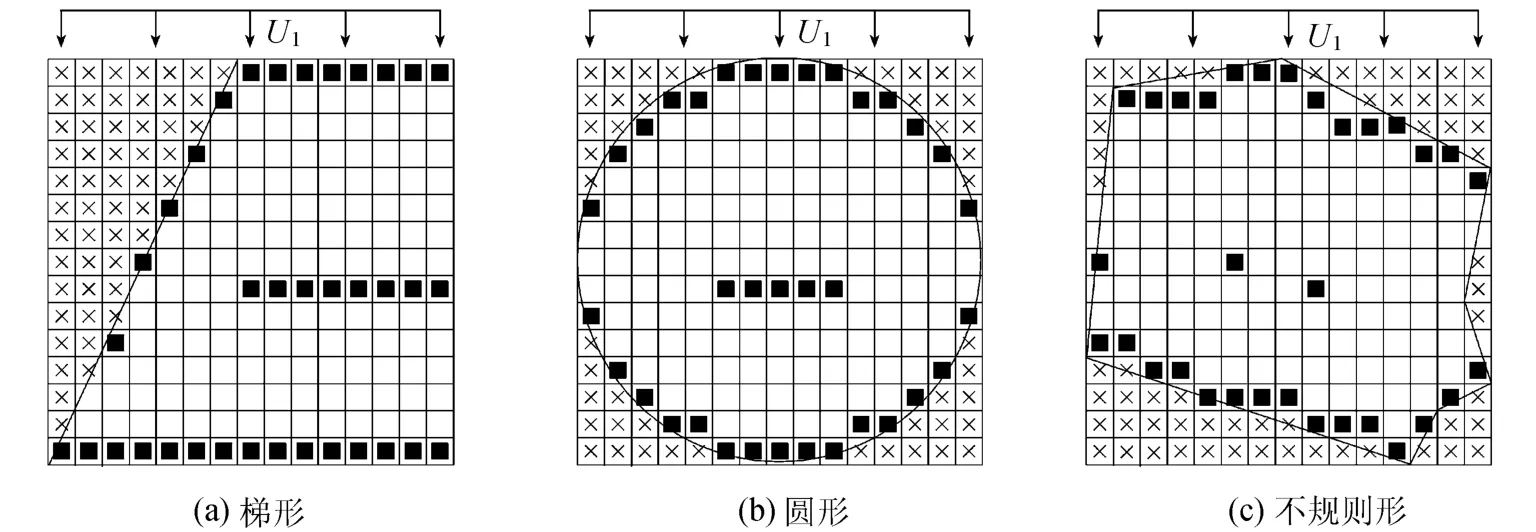
图6 单一风向下风电场风机最优布置方案Fig.6 Optimal configurations of wind farms under single wind direction condition

由图6可见,对于梯形、圆形和不规则形状的风电场,由于风机布置位置受风场边界制约,最优布置方案与方形风电场略有差异,但其最优布置方案所体现的风机布置规律与方形风电场基本一致,即本文上述给出的风机最优布置规律也适用于不规则形状的风电场.

2 其他典型风况下的风机最优布置规律

风电场最优风机布置与风况密切相关.典型风况中,除单一风向外,还包括均匀对称风向风况、1个主导风向风况和多个主导风向风况,其风玫瑰图如图7所示.

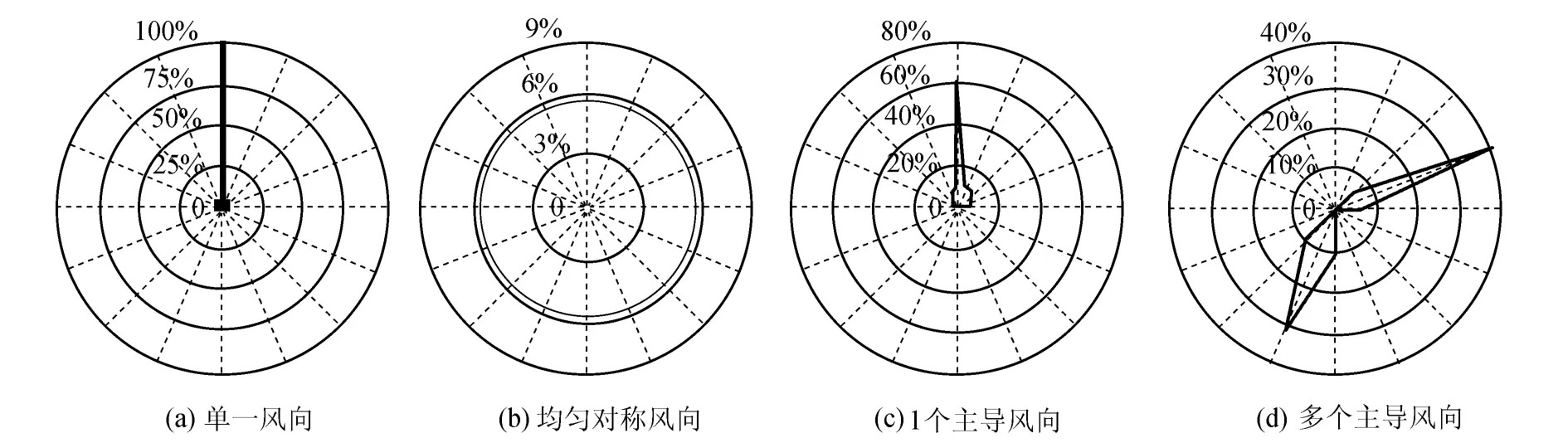
图7 典型风况的风玫瑰图Fig.7 Wind roses of typical wind conditions

2.1 均匀对称风向情况

在某些特殊地区,如草原、沙漠等平坦区域,全年各个方向的来风以及概率均相等或相差不大,其风况主要体现为均匀对称风向.此时,上述算例的风机优化布置计算结果如图8所示.

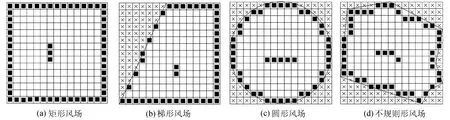
图8 均匀风向下风电场风机最优布置方案Fig.8 Optimal configurations of wind farms under uniform wind direction condition

对于均匀对称风向风况,不同形状风电场中风机最优布置的规律性较强,基本表现为沿风场区域边缘对称布置的形式.当风机数量较多时,除边缘风机外,其余风机布置在风场中央区域.

2.2 1个主导风向情况

根据实际风场的风能资源情况,在我国大部分地区(如四类风资源区),多数风电场的风况是1个主导风向风况.对于这种情况的风电场风机最优布置计算结果如图9所示.

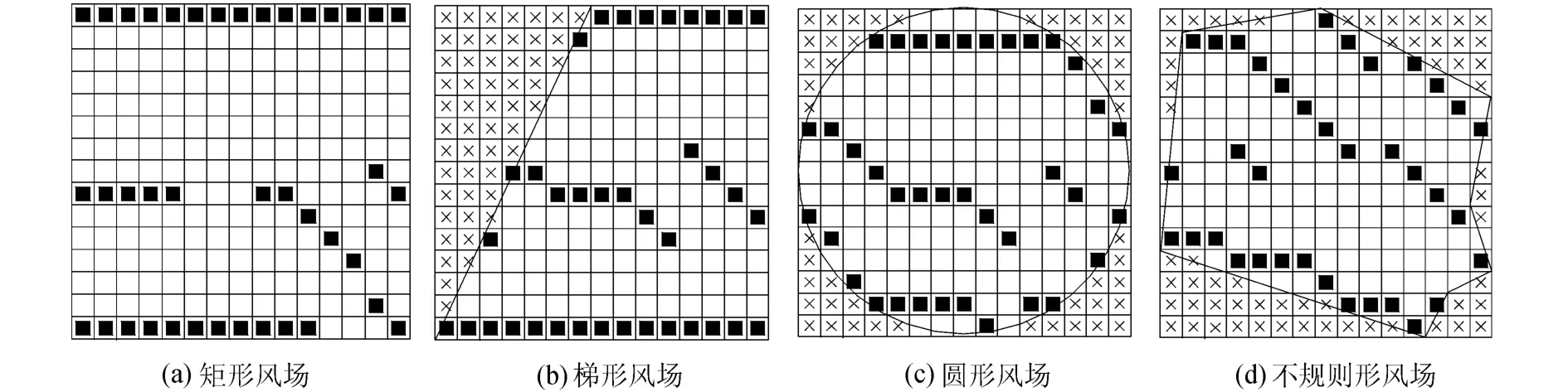
图9 1个主导风向下风电场风机最优布置方案Fig.9 Optimal configurations of wind farms under single wind direction dominated condition

对于1个主导风向的风电场,其风机最优布置规律主要体现在:主导风向概率越大,风机最优布置方案越接近于对应该主导风向的风机最优布置形式,且沿主导风向的风机间距基本满足本文上述给出的风机最小间距的要求.对于这类风电场,在风机优化布置时,一般可先按单风向风况进行排布设计,然后根据主导风向的风能密度概率函数进行局部调整,最终确定风机最优布置方案.

2.3 多个主导风向情况

当地形比较复杂时,风电场可能由于地形以及障碍物等的影响,存在多个主导风向的情况.对于这种情况的风电场风机最优布置计算结果如图10所示.

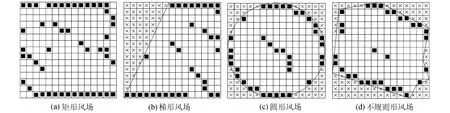
图10 多个主导风向下风电场风机最优布置方案Fig.10 Optimal configurations of wind farms under multiple wind direction dominated condition

对于存在多个主导风向的风电场,风况情况比较复杂,其风机最优布置规律性较弱.因此,对于这类风电场的风机最优布置设计,一般应通过详细的优化计算确定.

3 结 论

a.在风电场区域无限制的情况下,风机的横向间距应为2D0～3D0,纵向间距应大于15D0;当风机布置的排列数增加时,应逐步适当增大后排风机的纵横间距.

b.对于风电场区域确定的情况,单一风向风况下,风机最优布置方式一般为并行排列状形式.当风场区域在盛行风向上的尺寸较小(＜20D0)时,沿盛行风向一般布置1～2排风机,风机的最优纵向间距即为其可能的最大值,风机的横向间距应为2D0～3D0;当风场区域在盛行风向上的尺寸较大(＞20D0)时,风机沿盛行风向可考虑布置3排或3排以上,此时,风机纵向间距应为15D0～20D 0,风机横向间距应为3D0～5D 0.

c.在实际风电场风机优化布置时,一般可不考虑风速大小变化的影响.

d.针对不同风况、不同边界形状的风电场,风机最优布置体现出的规律性有所不同.均匀对称风况下,风机最优布置沿风电场边缘对称分布;单一主导风向风况下,风机最优布置为对应主导风向下的风机最优布置形式与其他非主导风向下的风机优化布置形式的组合,且主导风向的概率越大,最优布置方案越接近于该主导风向下的风机最优布置方案;对于多个主导风向风况,风机最优布置的规律性较弱,其最优布置方案一般应通过详细的优化计算确定.

[1]FRANDSEN S,BARTHELMIE R,PRYOR S,et al.Analytical modelling of wind speed deficit in large offshore wind farms[J].Wind Energy,2006,9(1/2):39-53.

[2]CHRISTIANSENM B,HASAGER C B.Wake effects of large offshorewind farms identified from satellite SAR[J].Remote Sensing of Environment,2005,98(2/3):251-268.

[3]VERMEERL J,SORENSEN JN,CRESPOA.Wind turbinewake aerodynamics[J].Progress in Aerospace Sciences,2003,39:467-510.

[4]PATELM R.Wind and power solar systems[M].Boca Raton:CRCPress,1999.

[5]王承煦,张源.风力发电[M].北京:中国电力出版社,2002:131.

[6]AMMARA I,LECLERC C,MASSON C.A viscous three-dimensional differential/actuator-disk method for the aerodynamic analysis of wind farms[J].JSol Energy Eng,2002,124(4):345-356.

[7]MOSETTIG,POLONIC,DIVIACCOB.Optimization ofwind turbinepositioningin largewind farmsby meansof agenetic algorithm[J].JWind Eng Ind Aerodyn,1994,51(1):105-106.

[8]GRADY SA,HUSSAINIM Y,ABDULLAHM M.Placement of wind turbines using genetic algorithms[J].Renewable Energy,2005,30(2):259-270.

[9]MARMIDIS G,LAZAROU S,PYRGIOTI E.Optimal placement of wind turbines in a wind park using Monte Carlo simulation[J].Renewable Energy,2008,33(7):1455-1460.

[10]王丰.风电场风能资源评估及风机优化布置研究[D].南京:河海大学,2009.

[11]BURTON T,SHARPE D,JENKINSN,et al.Wind energy handbook[M].England:John Wiley&Sons,2001:68.