遗传算法在水力管网优化中的应用

张 进,王卫敏,荆振锋,赵有民

(1.陕西城镇规划建筑设计研究院,西安710068;2.西安建筑设计研究院,西安710054;3.延安热电厂,延安716000)

0 引言

水力管网优化的实质是,在水力约束条件下,确定使目标函数即综合费用 (包括初投资和设计年限内的运行费用)为最小的变量 (管径)。这类问题在数学分析中称为极值问题,在统计数学中称为最优化问题。传统的求解非线性优化问题的方法对管网优化模型进行求解时必须先假设管径是连续变量,同时在求解过程中必须对目标函数进行求导,因此,在实际应用中受到了限制。本文尝试将遗传算法应用到水力管网的优化中,相对于传统的优化方法,遗传算法直接针对实际规格的管径,计算简便易行,只包括复制、交叉、变异这几个简单的过程。

1 遗传算法简介

遗传算法其实质是一种由计算机完成主要计算过程的迭代方法。遗传算法起源于20世纪60年代对自然和人工自适应系统的研究[1],最早由美国密执安大学的Holland教授提出。遗传算法借鉴了达尔文的自然进化理论与孟德尔的遗传变异理论,通过选择一定数量的个体进行杂交以及基因突变,把优秀的基因传给后代,丢弃不良基因,经过数代遗传,最终得到最优秀的一个或几个后代 (问题的最优解)。

遗传算法已用于求解带有应用前景的一些问题,例如遗传程序设计、函数优化、排序问题、人工神经网络、分类系统、计算机图像处理和机器人运动规划等。遗传算法经过很多人的改良也产生了很多变种,本文所涉及的遗传算法仅指 “简单遗传算法”简称SGA。与传统优化算法相比,SGA具有以下特点[2]:(1)搜索过程不直接作用在变量上,而是作用在将变量编码后的字符串上;(2)搜索过程从一组解迭代到另一组解,降低了陷入局部最优解的可能性;(3)搜索过程是随机的而非确定性的;(4)对搜索空间没有任何特殊要求,不需要导数等其它辅助信息。

2 遗传算法解决优化问题的主要步骤

从技术经济观点来看,任何输配系统的方案,均可用工程造价和运行费用来评价。

2.1 管径编码

编码是遗传算法的第一步,采用二进制编码方案。为便于讨论,水力管网的管材选用无缝钢管(GB8163-87)系列,实际应用时选用其他管材无非价格不同而已。取8种规格的钢管进行编码,如表1所示。

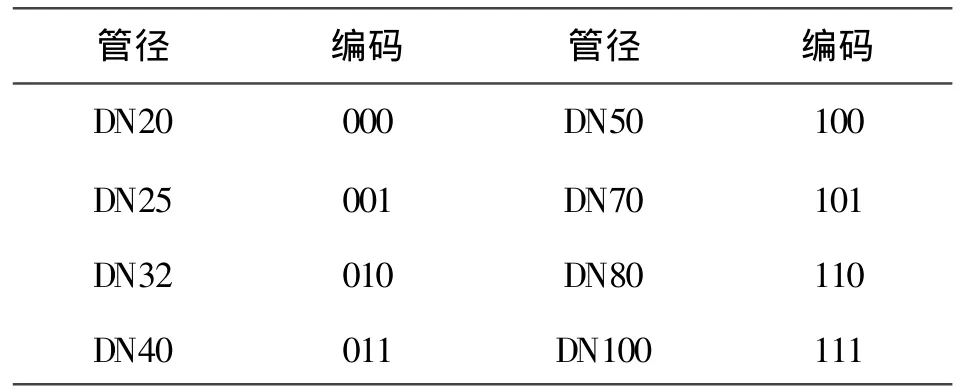
表1 管径编码表

2n种规格的钢管编码便有n位。

管径编码完成后,管网的设计方案即可用按管段编号顺序排列的一串0,1字符表示。例如,由8根管段组成的管网的公称管径按管段号排列依次为:20,25,25,32,40,32,70,80,那么对应的二进制表示的字符串则为:000|001|001|010|011|010|101|110。这个二进制字符串在遗传算法中称为遗传算子,也叫染色体。

以8根管段组成的管网为例,算法第一步就是随机产生一定数量的染色体,每个染色体为24位字节的二进制数即可。染色体总数叫种群规模,它对算法的效率有明显的影响,规模太小不利于进化,而规模太大将导致程序运行时间长。建议对管网优化问题,此规模取30至100。

2.2 适应度函数

为了体现染色体的适应能力,引入了对问题中的每一个染色体都能进行度量的函数,叫适应度函数。通过适应度函数来决定染色体的优、劣程度,它体现了自然进化中的优利劣汰原则。

管道的初投资取决于材料费和安装费。管道的安装费在管道敷设深度、土壤和路面性质、管子连接方法、施工机械化程度确定后则由管径决定,一般来说管径变化对安装费影响不大。

管网的运行费用主要由电费和维修费组成,维修费受当地管理水平限制一般与初投资成正比,电费与流量和压降的乘积成正比,而压降在管径确定后则由流量决定。

工程实际中,已知管网总流量,给定各管段管径后,根据连续性方程,并联管段阻力相同和水力计算的经验公式可由电脑计算出各管段流量。有了管径和流量就可以计算出初投资和设计年限内的运行费用 (也由电脑自动完成),得出费用评价函数W=∑[f(di)+g(di,qi)]。式中f(di)为初投资费用,是管径的函数,单位为元。g(di,qi)为运行费用,是管径及流量的函数,单位为元。di为各段管径,单位为mm。qi为各段流量,单位为吨每小时。

可见每个染色体唯一对应一个综合费用,从而可以用综合费用评价染色体的优劣。管网优化计算中应该费用越低则适应度越大,才能达到管网优化的目的。按照这个要求,通常可以将适应度函数取为与费用评价函数W成反比,即:f=1/W,也可取与W平方成反比。

2.3 遗传操作

简单遗传算法的遗传操作主要有三种:选择、交叉、变异。

2.3.1 选择操作 选择的目的是把优化的染色体直接复制到下一代或通过配对交叉产生新的染色体再遗传到下一代。这里采取配对交叉遗传的方式。选择机制为适应度比例选择机制,也叫赌轮或蒙特卡罗选择。在该机制中,每个染色体的选择概率为其适应度值除以所有染色体适应度值之和,适应度值大的染色体被选择的几率较高。同时,采用最佳个体保存方法,把群体中适应度值最大的染色体不进行配对交叉而直接复制到下一代中,这样,可以保证产生的新一代群体的最大适应度值不会小于上一代。Radolph在文献 [3]中证明了遗传算法不一定收敛,只有每代保存了最优个体时才收敛。在实际应用中,使用了上述结论来保证收敛性。采用优秀个体保护法就是将每代中的最优个体,直接进入子代。

对保存最优个体时遗传算法是收敛的结论的证明是通过对遗传算法构造马尔柯夫 (markov)链,因为遗传算法的进行过程是一个马尔柯夫过程。

注:马尔柯夫链。状态是指某一事件在某个时刻 (或时期)出现的某种结果。事件的发展,从一种状态转变为另一种状态,称为状态转移。在事件的发展过程中,若每次状态的转移都仅与前一时刻的状态有关,而与过去的状态无关,或者说状态转移过程是无后效性的,则这样的状态转移过程就称为马尔柯夫过程。马尔柯夫链是参数t只取离散值的马尔柯夫过程。

2.3.2 交叉操作 交叉是模仿自然界有性繁殖的基因重组过程,其作用是将原有的优良基因遗传给下一代个体,并生成包含更复杂基因结构的新个体。交叉操作是遗传算法区别于其他所有优化算法的根本所在,如果从一个遗传算法中去掉交叉操作,则其结果将不再是一个遗传算法[4]。

交叉操作是将被选择出的两个个体P1和P2作为父母个体,将两者的部分码值进行交换。对于24位的染色体:由电脑随机产生一个在1到24之间的随机数c,假如现在产生的是3,将P1和P2的低3位交换:P1的高21位与P2的低3位组成一个新染色体,这就是P1和P2的一个后代Q1个体;P2的高21位与P1的低3位组成另一个新染色体,这就是P1和P2的一个后代Q2个体。

2.3.3 变异操作 变异是模拟自然界生物体进化中染色体上某位基因发生的突变现象。变异可以使搜索避免陷入局最优,可以在当前解附近找到更好的解,同时还可以保持群体的多样性,确保群体能够继续进化[4]。

对于24位的染色体:由电脑随机产生一个在1到24之间的随机数d,假如现在产生的是3,将原染色体的第3位0和1互换产生一个新染色体。

2.3.4 操作的控制参数 不是每个被选择了的染色体都进行交叉操作和发生变异,而是以一定的概率进行,一般在程序设计中交叉发生的概率要比变异发生的概率选取的大若干个数量级,交叉概率取0.6至0.95之间的值;变异概率取0.001至0.01之间的值。个人建议设定一大一小两个变异概率,当整个种群平均适应度增长较快时,使用小变异概率;反之使用较大变异概率。

2.4 算法的终止条件

遗传算法的一般循环终止条件为设定最大进化代数,个人建议取50～80次。也可以把解的质量作为判据,如连续几次得到的最优个体的适应度没有变化或变化很小时,则认为算法收敛,循环终止。再次,种群中最优个体的适应度和群体的平均适应度的差除以群体平均适应度,所得的结果小于某一给定允许值,也可以作为循环终止的条件。

2.5 染色体解码

终止后输出种群中适应度值最优的染色体,对其进行解码得到管网各管段的管径。解码就是管道编码的逆运算。

2.6 遗传算法解题步骤的总结

根据遗传算法思想可以画出如图1所示的简单遗传算法框图。

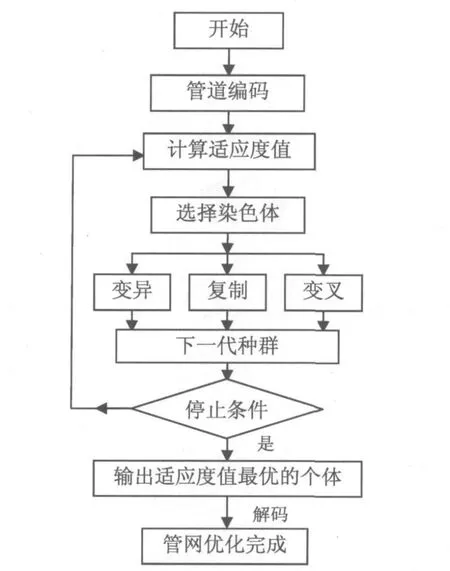
图1 简单遗传算法示意图

遗传算法的主要步骤如下:

(1)随机产生一个由确定长度的染色体组成的初始群体。

(2)对该染色体群体迭代地执行下面的步骤①和步骤②直到满足停止准则为止:

①计算群体中每个染色体的适应值;

②应用复制、交叉和变异等遗传操作产生下一代群体。

(3)达到终止条件后,把后代中出现的最好的染色体输出为遗传算法的执行结果,这个结果可以解码为问题的一个解。

2.7 算例描述

某管网连接图见图2。共有7个节点,6条管道连接路线。管网中各个节点需水量和长度见图示,管道单价经验公式为:

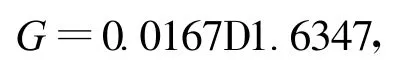
管径D的单位为mm,适应度函数取为与费用评价函数W成反比,即:

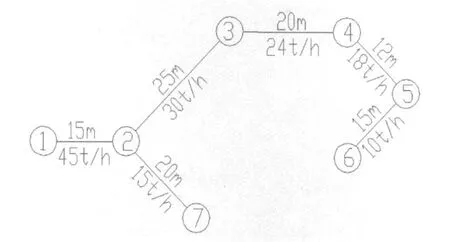
图2 某管网连接图

对此管网应用遗传算法进行优化布置,设置群体规模为30,设定最大进化代数为50代,进行计算。

以下列出最后三步的最优解 (见表2)。

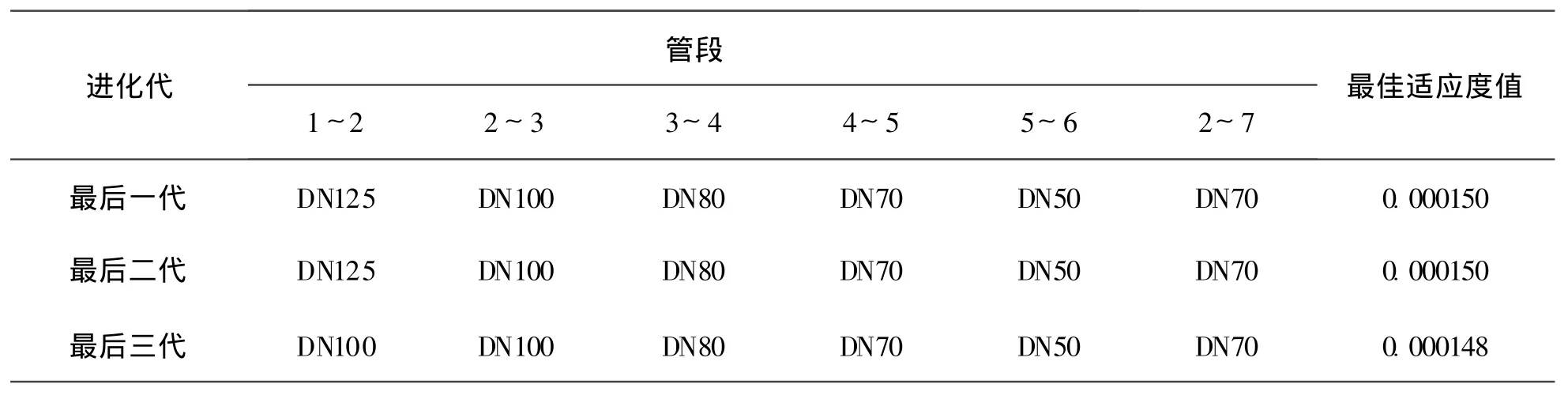
表2 最后三步的最优解

3 结语

遗传算法在计算结果以及收敛速度方面具有优势,但是算法的参数选取直接影响到算法的效果,需要进一步研究。

此外,管网系统是个复杂的系统工程,本文中未对当地水文地质条件、政策、物价的波动等因素做深入考察,需要进一步研究加以完善。

[1] HOLLAND J H.Adaptation in nature and artificial systems[M].Michigan:The University of Michigan Press,1975

[2] 周明,孙树栋.遗传算法原理及应用 [M].北京:国防工业出版社,1999

[3] Qi X F;Palmieri theoretical analysisof evolutionary algorithms with an infinite population size in continuous space(Part,)[M].IEEE Transactions on Neural Network;1994

[4] 张铃,张钹.遗传算法机理的研究[J].软件学报,2000,(7):945-952