表上作业法优化土方调配方案解析
□李长安(河南省水利水电学校)
□李新辉(登封市建设管理局)
一、表上作业法求解最优方案的步骤
(一)作初始方案
初始方案应采用“最小元素法”,即在运算过程中对运距最近的先满足其所需土方量,以此为基础把土方分配完毕,并把各运距及需调配的土方量列表体现。
(二)判断初始方案是否最优
最优方案判断的方法是“全部检验数≥0”。首先根据初始方案表作出位势表,位势表中的空格用矩形法求出,即构成矩形的两条对角线上的数据之和相等,以此把空格补齐。其次作检验表。检验表中的数值是用初始方案中各项运距值减去位势表中相对应的运距值,如果检验表中的数值全部大于或等于零,则说明初始方案即是最优方案,如果有一项小于零,则说明初始方案不是最优方案,这时就需要对方案调整优化。
(三)优化调整初始方案
1.作调整方案表
在初始方案中,由检验数为负数的方格(如果有几个负数,用绝对值最大的方格)开始,作一闭合回路。即从该方格出发,沿水平或垂直方向前进,每到数字的方格可以(并非必须)转90°再继续前进,最终回到出发点方格,形成一个闭合回路。在闭合回路上以起点为“0”按行走路线依次编号,并在编号为奇数点的方格中,选其中数最小的土方量作为“调整量”。然后,将所有奇数点的方格中的土方量减去调整量,偶数点方格中的土方量加上调整量,即得到调整方案表。
2.作检验表判断调整方案是否最优
根据调整方案表,依次分别作出位势表和检验表。如果检验表中的所有数据都大于或等于零,则该方案即为最优方案,否则继续调整。
二、土方调整方案优化调整实例
现有一场地平整工程,调配区内共有4个挖方区和3个填方区,现已做出初始方案见表1,(表内小方格内的数据为各填方区与各挖方区之间的运距,大方格内的数为初始方案中挖方区到填方区调配土的数量)。判断并找出最优方案。
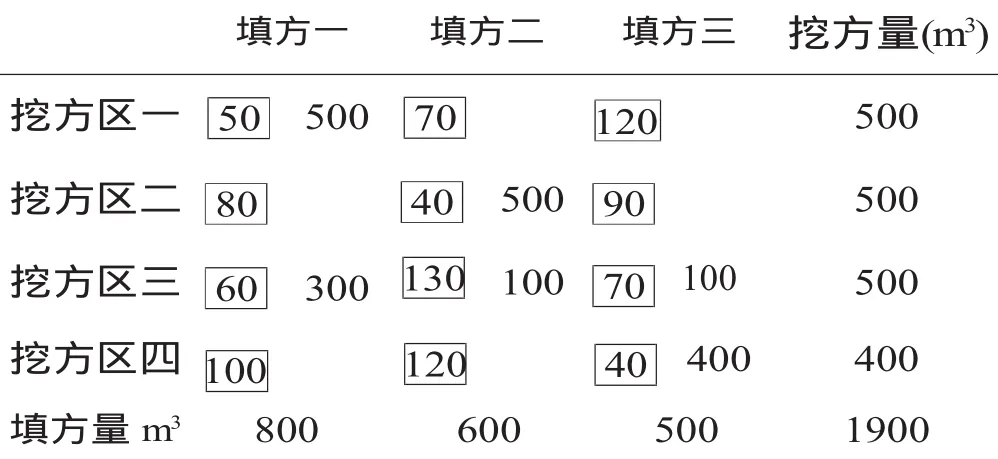
表1 土方调配初始方案表
(一)判断该初始方案是否最优
1.作位势表见表2,表中括号内的数值是初始方案表中有土方运输关系的挖、填区的运距,其余为按矩形法补齐的数据。

表2 位势表
2.作检验表见表3。表中数据为初始方案的运距值减去位势表中的数值而得出。

表3 检验表
由于检验表中-50<0,所以该初始方案不是最优方案,需要调整优化此方案。
(二)调整优化初始方案
1.做调整方案表
在初始方案表中,以检验表中-50所对应的方格开始作闭合回路,并得出调整量就是编号为第三个角点的土方量,即100m3,如表 4。
在闭合回路中,奇数点中土方量减去100,偶数点中土方量加上100,即得到调整方案表如表5。

表4 土方调配调整方案表
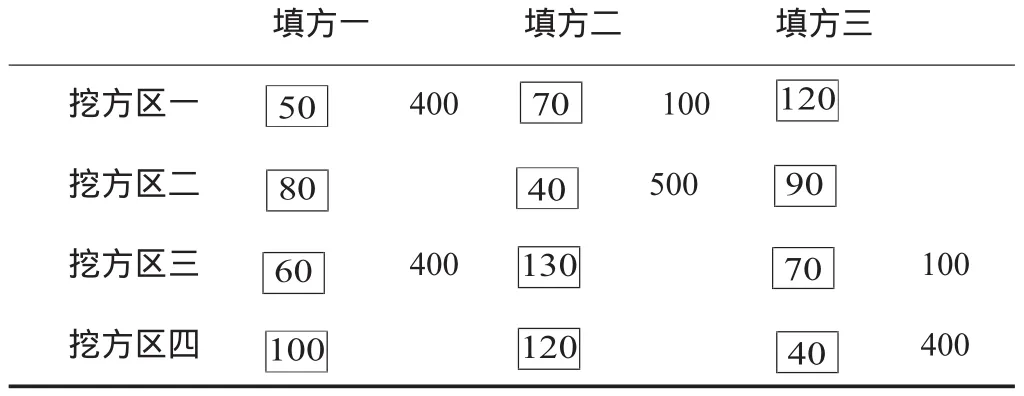
表5 土方调配调整方案表
2.判断调整方案是否最优
首先,作位势表,由调方案表5中有土方运距关系的远距数值填入表中,其余空格用矩形法求出,见表6。
第二,作检验表,由调整方案表5中的运距减去位势表中相应的数值即得检验数,见表7。

表6 位势表
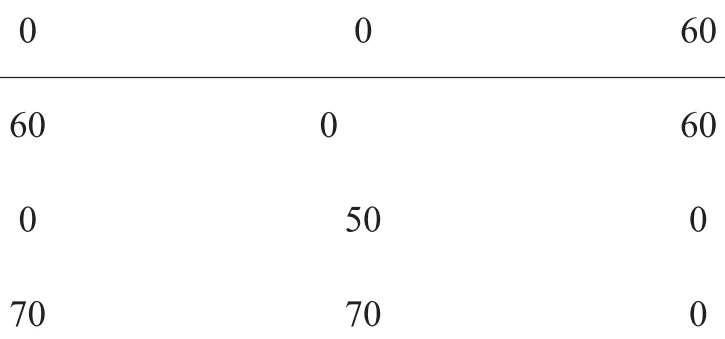
表7 检验表
由表7可以看出,表中所有数值均≥0,因此该调配方案为最优方案。

