LDPC编码中大矩阵求逆及存储的一些方法*

许帮保 ，刘春江，郭沛宇，王 昱

（1.国家广播电影电视总局 广播科学研究院，北京 100866；2.海军91917部队 海军指挥自动化机房，北京 100000）

1 引言

近年来前向纠错功能优越的低密度奇偶校验（LDPC）码[1-4]在 CMMB[5]、地面数字电视国标、DVB-S2[6]等标准中得到成功应用。由于LDPC码的优势在码长较长（数以千比特）时才较明显[3]，所以实用LDPC码的码长多数在10000 bit左右。加上要满足多种码率的要求，LDPC编码会遇到大矩阵求逆及存储方面的问题。

若LDPC编码器将长度为k的信息比特 m=（m0，m1，m2，…，mk-1）编码为一个长度为n的LDPC码字C=（m，p）＝（m0，m1，m2，…，mk-1，p0，p1，p2，…，pn-k-1），其中 p 为校验位，设LDPC码的奇偶校验矩阵为H=[H1H2]，其中，H1子矩阵包括H矩阵中的前k列，H2子矩阵包括H 矩阵中的后（n－k）列，则可得校验位：

编码过程中，最大的运算量发生在H2的求逆（或线性方程组求解）过程中，虽然H是稀疏矩阵，但是一般不再稀疏，这会带来矩阵存储量大、占用存储资源较多的问题，在存储资源非常紧张的嵌入式应用和终端产品中非常难以实现。

2 LDPC编码中大矩阵的求逆及存储

2.1 设计特定结构的矩阵H2使具有规则的结构

进行LDPC编码时，通过行列变换等矩阵的初等运算使矩阵H2及具有特定的规则的结构，便于存储和计算。例：当码长为15360 bit=1920 byte，码率为3/4时，H2的阶为3840。设

式中：I表示256阶的单位阵，O表示256阶的零阵，256阶的矩阵A和B定义为

A，B的定义中I表示32阶单位阵，O表示32阶零阵，R表示32阶单位阵的1位循环右移阵。A和B仍为行重及列重均为1的可逆阵，且B=A2。H2前256列的列重为 3，后256×14（即 3584）列的列重为 2。 此处 H2的结构是DVB-S2[7]中所采用的LDPC校验矩阵H2部分的改进，经过改进之后原有的一列列重为1的列变为列重为3，255列列重为2的列变为列重为3，提高了LDPC码的纠错效率。

因为 R-1=RT，所以 B-1=BT=A-2。 设 C=I+R-1+R-2，则 C可逆。设D=I+A-1+A-2，可求得

则可用消元法求得H2的逆，及 I+B-1D-1构成，=矩阵1+矩阵2，其中矩阵1为15×15的分块阵，上8行的每个元素均为B-1D-1，下7行的每个元素均为D-1；矩阵］，其中 Δ1是 8×8的分块下三角阵，下三角元素（不含对角线）均为256阶单位阵，Δ2是7×7的分块上三角阵，上三角元素（含对角线）均为256阶单位阵。

首先计算u=H1mT，信息向量mT为11520维列向量，H1为 3840×11520 的稀疏矩阵，u=H1mT为 3840维列向量。 设，u1，u2，…，u15均为 256维列向量，最后得到pT=。

对 应 码 率 r=1/4，2/5，1/2，3/5，2/3，3/4，4/5，5/6，13/15，9/10，码长为N=1920×8=15360的校验矩阵H中，H2为阶为 M=（1-r）×N=256×m 的方阵，m 分别为45，36，30，24，20，15，12，10，8，6。 此处略去其他码率对应的H2，及p的计算。由于各码率对应的共用 D-1，B-1D-1，因而多码率的实现并没增加多少存储负担。

由循环右移1位的32阶矩阵R的特性，使硬件实现QC-LDPC编码[8]更方便。列重为3的H2可类似构造使仍具一定的结构。当然，必须考虑LDPC解码纠错效率，不能出现Tanner图中围长为4的情形。设

以上列重为3的H2的逆的LU分解形式为

对应码率r为0.1～0.9之间间隔0.05的所有值，码长为15360的LDPC编码中的均有类似结构。

2.2 Richardson和Urbanke的方法（RU Alogrithm）

Richardson和 Urbanke[4，9]指出通过对 LDPC的校验矩阵进行一定规则的线性操作即预编码的算法（RU Alogrithm），可以使LDPC编码器的复杂度控制在与码长成线性关系。

设码字矢量 x=（s，p1，p2）， 其中 s 为信息位，p1与 p2合起来表示校验位，利用校验方程Hx′=0来计算p1和p2。RU算法主要包括离线预处理和实际在线编码两个步骤。预处理通过行列置换把校验矩阵H转化为近似的下三角阵形式H′，预处理只需执行一次，可以在软件中离线预先处理。然后把H′分成6个稀疏矩阵，通过分步计算求得 p1和 p2，其中 p1复杂度为 O（N+g2），p2的计算复杂度为O（N）。图1为H经预处理后的近似下三角阵形式 H′。

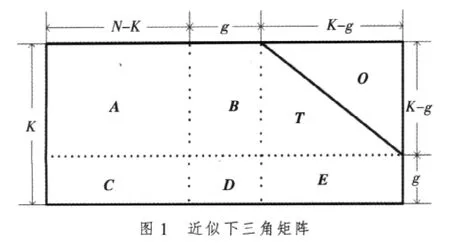
对H的行变换不影响LDPC编码。列的置换对应码元的比特影射。经行变换及列置换可使矩阵T的阶尽可能地大，矩阵D的阶尽可能地小。

文献[4]中对列重为3，行重为6的H预处理后所得D的阶g可小到码长N的0.017倍。这为码长近10万的LDPC码编码提供了可行的方法。列重为3的H经预处理后所得最小的g为2。当g很小时，LDPC编码具有近似线性复杂度。

2.3 H经行（列）置换后T虽不为下三角阵但T-1易求且稀疏

以CMMB中码率为3/4的LDPC编码为例，码字比特影射向量对应校验矩阵的列置换，设经列置换后的校验矩阵为H=（H2H1），仅对H作适当的行的位置变换后，H就可化为其中A，B，C，D，E，X1，X2，X3均为稀疏矩阵。 A，E 的行重不过11，B 的行重不过 6，X1的行重不过 1，X2的行重为 1，X3的行重不过 3，各矩阵的列重不过 3。 I1393，I54，I43，I122分别表示阶为1393，54，43，122的单位矩阵。T为1612阶方阵，相应的A为1612×6912稀疏阵，B为1612×692稀疏阵，C为692×6912稀疏阵，D为692×692稀疏方阵，E为692×1612稀疏阵。虽然此处T不为下三角矩阵，但易知T-1为

因 X2X1=0，X3X1（行重不过 3）仍为稀疏矩阵，故T-1（行重不过7）仍为稀疏矩阵。ET-1B，ET-1A仍为稀疏。离线计算稀疏阵D+ET-1B，稀疏阵C+ET-1A和（D+ET-1B）-1（该逆阵的元素量约为的 9%）。 在线计算（C+ET-1A）s，在线计算得

与RU算法相比，这样可减少在线计算从而减小编码延时，但需要适当增加存储（如果考虑列的置换及行消元，可使T的阶增大，D的阶减小）。

2.4 对H2进行LU分解后再迭代求解

采用优化的部分主元法对H2进行LU分解所得下三角阵L及上三角阵U可能是稀疏的，从而仅需较小的存储空间[10]。文献[10]中L和U的非零元总数只约占元素总数的0.25%，再经在线前向和后向迭代运算得校验比特向量。

3 结论

[1]GALLAGER R G.Low-density parity-check codes[M].Cambridge，Massachusetts：M.I.T.Press，1963.

[2]MACKAY D J C.Good error correcting codes based on very sparse matrices[J].IEEE Trans.Inform.Theory，1999，45：399-431.

[3]RICHARDSON T J，SHOKROLLAHI M A，URBANKE R L.Design of capacity-approaching irregular low-density parity-check codes[J].IEEE Trans.Inform.Theory，2001，47（2）：619-637.

[4]RICHARDSON T，URBANKE R.Efficient encoding of low-density parity-check codes[J].IEEE Trans.Inform.Theory，2001，47 （2）：638-656.

[5]GY/T220.1-2006，移动多媒体广播 第1部分：广播信道帧结构、信道编码和调制[S].2006.

[6]Digital Video Broadcasting（DVB）.ETSI EN 302307 v1.1.1（2004-06），Second generation framing structure，channel coding and modulation for broadcasting，interactive services，news gathering and other broadband satellite applications[S].2004.

[7]Digital Video Broadcasting（DVB）.ETSI TR 102307 v1.1.1（2005-02），Annex A，A.1，Second generation framing structure，channel coding and modulation for broadcasting，interactive services，news gathering and other broadband satellite applications[S].2005.

[8]刘春江，吴智勇，于新，等.一类准循环LDPC码的快速编码方法[J].电视技术，2007，31（6）：11-13.

[9]袁东风，张海刚.LDPC码理论与应用 [M].北京：人民邮电出版社，2008.

[10]黄荔杰，唐晓晟.CMMB系统中HS-LDPC编码的实现[EB/OL].（2009-07-10）[2009-10-07].http：//www.paper.edu.cn/index.php/default/releasepaper/content/33773.