Overview of Upheaval Buckling Theoretical Studies for Submarine Buried Pipeline
Overview of Upheaval Buckling Theoretical Studies for Submarine Buried Pipeline
Pipelines constitute a vital means of transporting and distributing liquids and gases such as oil,gas and water over large geographical areas.A pipeline containing hot oil(and possibly insulated in order to prevent the solidification of wax in the pipe)will expand longitudinally on account of the rise in temperature;and if such expansion is resisted,for example by frictional affects over a kilometer or so of pipeline;compressive axial stress will be set up in the pipe-wall.The compressive forces are frequently large enough to induce lateral buckling of untrenched pipelines,or vertical buckling of trenched pipelines.The recent growth in interest in high temperature pipelines in China and some failures in Bohai Gulf have led to an explosion of interest in these phenomena for Chinese ocean engineers.This paper describes the history of the theoretical studies on the submarine buried pipeline vertical buckling and the author’s experiences with this problem.
submarine pipeline;trenched;buried;upheaval buckling
Biography:GAO Xi-feng(1975-),male,Ph.D.,lecturer of Tianjin University;Corresponding author:LIU Run(1974-),female,Ph.D.,Professor,E-mail:liurun@tju.edu.cn.
1 Introduction
Since the early seventies of the last century pipelines have also become one of the main means of transporting oil and gas offshore in many parts of the world.To ensure minimal interference with other marine activities,such as fishing nets,ship anchors,etc and to ensure safety of the structure and the environmental,the pipelines are usually buried in a trench.The present paper will pay more attention on the pipeline vertical,upheaval buckling.The first paper on pipeline buckling in the open literature appeared in 1974.Palmer and Baldry[1]demonstrated that the constraint of expansion of a pipeline on account of raised internal pressure could induce buckling through a small-scale test.Hobbs[2-3]presented a summary of the basic models of buckling in a long pipeline in 1981 and 1984.An explosion of interest has been induced in pipelines thermal buckling in the early eighties of the last century as some upheaval buckling incidents occurred in the North Sea.As Guijt[4]pointed out that at least five upheaval buckling incidents occurred in the North Sea,three of which occurred in 1989,and all with significant cost penalties.The first incident,associated with Maersk Oilog Gas AS’Rolf pipeline,occurred in 1986[5].The cost of a failure in such a pipeline is so high,not only for repairs but also for lost production.Therefore from then on,the question of thermally induced buckling is of considerable economic importance,and a substantial literature has built up in the following 30 years.The papers presented at a special session of the 1990 Offshore Technology Conference are perhaps the best explanation that the pipeline buckling research is a hot topic in this area.The 22nd Annual OTC also implied that the subsea pipeline buckling researches reach to peak at that time.Century 90’s up to date,the theoretical and experimental studies on the subsea buried pipeline buckling are continued.The basic models presented by Hobbs[3]have been modified and refined with considering the pipeline imperfection[6-12]and the elastoplastic behaviour of buckling pipelines[13-14].Furthermore,the numerical method has been applied to analyze the pipeline buckling behavior[15-17].This paper describes its development,and its relation to today’s applications for upheaval studies.
2 Theoretical solutions for perfect straight pipelines
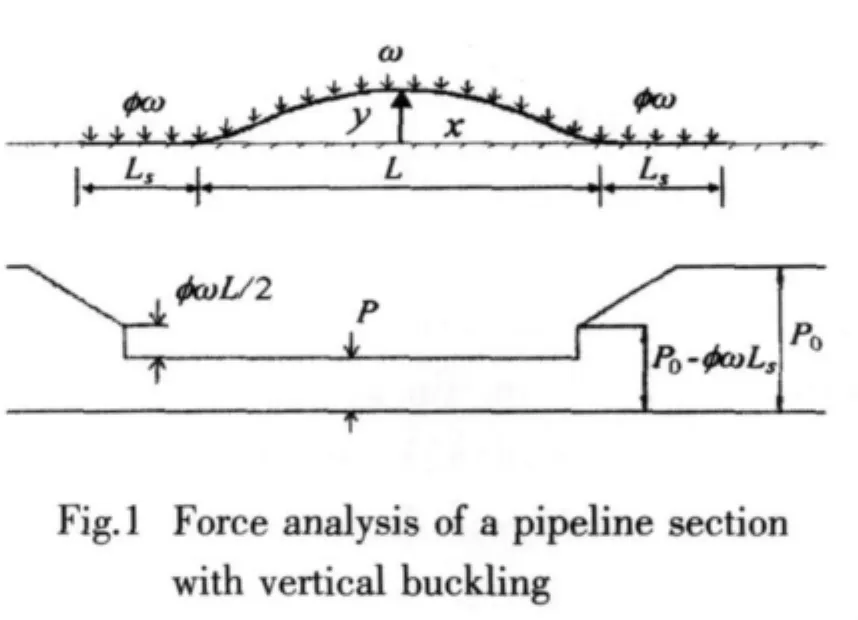
The compressive stress required to buckle a straight,pin-ended column(‘Euler buckling’)is inversely proportional to the square of the slenderness of the column;and it is obvious that all pipes are very slender over sufficiently large lengths.Submarine pipelines often carry products which are much hotter than the surrounding seawater.The potential thermal expansion is restrained by friction between the pipeline and the seabed,causing the development of large compressive axial forces in the line,which can lead to Euler buckling of the pipeline.Similar problems occurred in railway tracks more than 70 years ago,and the percipient analysis by Martinet and the extensive literature summarized by Kerr[18-19]are very closely related to the thermal buckling problems in pipelines.Hobbs[2-3]presented a summary of the basic models of buckling in a long pipeline(Ref.to Fig.1).
In the model,denoting the cross-sectional area of the pipe by A,Young’s modulus by E,the coefficient of linear thermal expansion by α and the temperature change by ΔT.The force created by full restraint of thermal expansion is,

If the axial strain ε is completely restrained,the axial compressive force generated and available to participate in buckling is,

where υ is Poisson’s ratio,p is the internal pressure,and t and r are the pipe wall thickness and radius respectively.
A linear differential equation has been established to describe the deflected shape of the buckled part of the pipeline which is treated as a beam column under uniform lateral load.It is assumed that the bending moment at the lift-off point is zero.In the notation of Fig.1,

where m=w/EI,n2=P/EL and w is submerged weight of pipeline(including weight coat)per unit length.
The equation is solved and the following results are obtained:

where P is the axial load in the buckle and P0is the axial load away from the buckle(Fig.1),φ is the coefficient of friction between pipe and subgrade.
The maximum amplitude of the buckle

And the maximum bending moment,at x=0,is

A further result of practical interest is the size of the slipping length adjacent to the buckle,

Fig.2 is the vertical buckling result for a typical pipeline with a practical range of friction coefficients,0.2≤φ≤0.4,calculated by author with Hobbs’s model in Bohai Bay.The pipe has an outside diameter of 323.9mm,and a wall thickness of 12.7mm giving a design internal pressure 4.65MPa and design temperature rising 85℃.
Fig.2 shows that there exists the largest ‘safe’temperature change to avoid vertical buckling in this particular pipeline is about 45℃if the coefficient of friction φ is taken as 0.4.The curves in Fig.2 look like U-shape,that is to say,there are two possible buckle lengths for one temperature change.Hobbs[3]explained that the equilibrium path from A to B is unstable,which is a consequence of the assumption of fully mobilized friction even for vanishingly small displacement.The equilibrium path from B to C describes the relationship between the temperature and the buckle length for a pipeline with small imperfection.The temperatures against length of buckle and amplitude curves are the classical results in pipeline thermal buckling analysis until now.Nonetheless,as Hobbs[3]remarked,the model no account has been taken of the initial out-of-straightness and further numerical work on the effects of initial imperfections would be valuable.

3 Studies on imperfect pipelines
Engineering practice shows that the in-situ shape of a buried pipeline in the field is far from being straight.The imperfections concerned may include a crest in the sea bed profile,or a prop,as when isolated rock is located immediately below the line or another pipeline is to be crossed.Other less obvious possibilities include the free span gap or trench step,or an angularly mismatched field joint.With the initial imperfection,the pipeline may develop initial deformation.Under the temperature rising,upheaval may take place in the pipeline because of the existence of initial imperfection.Many researches have been done on imperfect pipelines,such as,Taylor and Gan[20],Boer et al[21],Friedman[22],Richards and Andronicou[23],Ju and Kyriakides[24],Pedersen and Jensen[25],Ballet and Hobbs[6],Taylor and Tran[7-8],Maltby and Calladine[9],Croll[11],Hunt and Blackmore[12].Among them,Taylor and Gan[20],Taylor and Tran[7-8],Maltby and Calladine[9]and Hunt and Blackmore[6]should be mentioned.Taylor and Tran(1996)summarized three basic types of initial imperfection for subsea buried pipeline,which are illustrated in Fig.3.
The initial imperfection is denoted by amplitude vomand wavelength L0or Lias shown.Whilst Liis determined from simple statics,L0is subject to individual engineering judgment.

The physical problems together with the key conceptual and mathematical models for each type of initial imperfection have been set out based on a stress-free-when-initially-deformed datum in the paper.And all models presume system symmetry and seabed trench-bottom rigidity,together with relatively small deformations and linear elastic properties.Similar analysis to perfect pipeline,internally generated temperature and pressure rises over ambient suffered by the pipe,ΔT and p respectively,in terms of the so-called pre-buckling force P0can be calculated by Eq.(1)and Eq.(2).
In the first case,so-called empathetic model,the pipeline remains in continuous contact with some vertical undulation in an otherwise idealized horizontal and straight line.The empathetic model employs idealized buckling mode to propose

where v0denotes imperfection displacement above the horizontal datum surface at x,0<x<L0,with v0m=,in conjunction with the unique amplitude/wavelength relationship also originating from idealized studies:

where w denotes the pipe’s submerged self-weight(or effective download)per unit length and I represents the pipe’s cross-sectional second moment of area.
Presuming fully mobilized friction resistance to be developed,the model definition is completed by means of the longitudinal equilibrium and compatibility expressions:

In accordance with the requirements of the potential energy theorem,the pipe buckling force Pein Eq.(11)can be obtained from

where P denotes the idealized buckling force.

In Eq.(12)Lsis the slip length and ufis the flexural end shortening

From Eqs.(1),(2)and(11)~(15),the relationship between temperature and buckle amplitude can be obtained.
The isolated prop alternatively features a sharp vertical irregularity such that voids exist to either side.The prop represents the undercrossing of a non-parallel pipe or the presence of an intervening rock;stop-start trenching procedures can also be responsible.Five key stages have been proposed in buckling development(Ref.to Fig.4).
As the temperature of the pipeline rises due to routine operation,the initial span or imperfection wavelength Lisuffers a reduction as the pipeline tightens up under compressive action P.The wavelength L reduces to some specific value Luwhereupon the pipeline lifts off the prop.Post-upheaval buckling initially involves wavelength Lu<L<Li,with L>Liensuing if circumstances so dictate.The associated differential equation for the initial imperfection takes the form


where Fiis the shear force acting at the crown.
Computational manipulation with boundary conditions gives the vertical deflection vias

In addition to the static determination of Liin terms of imperfection amplitude vi,equations for longitudinal equilibrium and compatibility together with an appropriate buckling/flexural expression are required for each of the phases(b),(d)and(e)shown in Fig.4.
For phase(b)the buckling/flexural expression is




And the differential equations for phase(e)are


The general solution to the buckling/flexural expression takes the following form

where the constants of integration c1and c2can be determined in accordance with the boundary conditions of each phase.
The characteristic equation reveals the relationship between nL and Li/L,which can be obtained by the further computational manipulation.Model definition of each phase is completed by means of longitudinal equilibrium and compatibility expressions of similar form to Eqs.(11)and(12).
The third case in Fig.3 occurs where the above voids become infilled with leaching sand and represents a special sub-case of the first.If marine conditions permit and particularly where continuous burial is involved,the prop-attendant voids discussed above can become infilled to the extent that the in-service,pre-buckling flexural stage is no longer effectively available.The post-upheaval buckling is divided into two stages.With L<Liin the early postbuckling phase,a vectorial equilibrium compatibility analysis is employed here by using the moment curvature relationship


In addition to establishing the above upheaval model for imperfection pipelines,Taylor and Tran(1993)developed the buckle model for protected pipeline,such as trenching and burial,continuous or discrete,together with the employment of fixed anchorages.
In all the calculations above,the buckle has been assumed to be completely symmetric.Ballet and Hobbs[6]investigated the possibility of asymmetric buckling in the prop case and found the results.Hunt and Blackmore[12]studied the effects of asymmetric bed imperfections,typified by a step and adopted a shooting method to solve the standard fourth-order linear ordinary differential equation.Comparison between two typical types,the prop and the step,implied that more profound destabilizing role can be attributed to the step than the prop.Maltby and Calladine[9]proposed a simple formula for the axial load at which the localization of buckling occurs based on sinusoidal imperfection assumption.

where p is the compressive force in pipe,Q0is the maximum value of soil resistance per unit length,and Y0represents the amplitude of initial imperfection.
Parametric studies of Empathetic models,employing the foregoing data in Bohai Bay,have been investigated with graphical comparison illustrated by Fig.5 for various initial imperfection amplitudes v0m,ranging from 50mm to 300mm.With regard to the respective temperature rise/buckling amplitude loci and the results given in Fig.5,it can be seen that only the relatively small imperfections typified by v0m=50 and 100mm display a maximum temperature together with the associated snap buckling phenomenon.The remaining four cases,v0m=150 to 300mm,generate stable post-buckling path.The safe temperature obtained by imperfect model is obviously lower than the one calculated by perfect model.

4 The future
The economic importance of submarine pipelines has greatly increased in recent years with the development of offshore oil and gas fields in many parts of the world.The vulnerability of pipelines to thermal stress is well documented in many case studies and review papers.Analysis and numerical modelling of pipelines upheaval buckling have progressed over the last thirty years,broadly from the classical analysis,to one covering initial imperfections,to one additionally covering material non-linearity,to one additionally including large pipe displacement and associated cover non-linearity.However,there are still some involved problems need to be dealt with.
The trend for offshore oil and gas extraction to take place in deeper and more remote waters is leading to the construction of longer pipelines that operate at higher temperatures and pressures.In shallow water,it is common practice to bury a pipeline for protection from trawl gear and to prevent buckling.However,in deep water,there is no requirement for burial,and it is more cost-effective to simply lay pipelines on the seabed.Without the lateral restraint the horizontal snaking is dominant for pipeline to relieve the thermal stresses.Therefore,the studies of pipelines lateral thermal buckling and the soil lateral resistance will become a hot topic for unburied submarine pipeline.
[1]Palmer A C,Baldry J A S.Lateral buckling of axially-compressed pipelines[J].Journal of Petroleum Technology,1974,26(11):1283-1284.
[2]Hobbs R E.Pipeline buckling caused by axial loads[J].Journal of Constructional Steel Research,1981,1(2):2-10.
[3]Hobbs R E.In-service buckling of heated pipelines[J].Journal of Transportation Engineering,ASCE,1984,110(2):175-189.
[4]Guijt J.Upheaval buckling of offshore pipeline:overview and introduction[C]//In proceedings of the 22nd Annual OTC.Houston,Texas,1990:573-578.
[5]Nielsen N J R,Lyngberg B,Pedersen P T.Upheaval buckling failures of insulated burial pipelines-a case story[C]//In proceedings of the 22nd Annual OTC.Houston,Texas,1990:581-592.
[6]Ballet J P,Hobbs R E.Asymmetric effects of prop imperfections on the upheaval buckling of pipelines[J].Thin-Walled Structures,1992,13:355-373.
[7]Taylor N,Tran V.Prop-imperfection subsea pipeline buckling[J].Marine Structures,1993,6:325-358.
[8]Taylor N,Tran V.Experimental and theoretical studies in subsea pipeline buckling[J].Marine Structures,1996,9(2):211-257.
[9]Maltby T C,Calladine C R.An investigation into upheaval buckling of buried pipelines--i.Experimental apparatus and some observations[J].International Journal of Mechanical Sciences,1995,37(9):943-963.
[10]Maltby T C,Calladine C R.An investigation into upheaval buckling of buried pipelines--ii.Theory and analysis of experimental observations[J].International Journal of Mechanical Sciences,1995,37(9):965-983.
[11]Croll J G A.A simplified model of upheaval thermal buckling of subsea pipelines[J].Thin-Walled Structures,1997,29(1-4):59-78.
[12]Hunt G W,Blackmore A.Homoclinic and heteroclinic solutions of upheaval buckling[J].Phil.Trans.R.Soc.Lond.,1997,355(4):2185-2195.
[13]Friedmann Y,Debouvry B.Analytical design method helps prevent buried pipe upheaval[J].Pipeline Industry,1992,11:63-68.
[14]Villarraga J A,Rodríguez J F,Martínez C.Buried pipe modeling with initial imperfections[J].Journal of Pressure Vessel Technology,2004,126(5):250-257.
[15]Zhou Z J,Murray D W.Behaviour of buried pipelines subjected to imposed deformations[C]//12th Int.Conference on Offshore and Arctic Engineering.ASCE,1993,II:115-122.
[16]Pasqualino I P,Alves J L D,Battista R C.Failure simulation of a buried pipeline under thermal loading[C]//Proceedings of the 20th International Conference on Offshore Mechanics and Arctic Engineering(OMAE),2001,OMAE2001-4124.Rio De Janeiro,Brazil,2001.
[17]Einsfeld R A,Murray D W,Yoosef-Ghodsi N.Buckling analysis of high-temperature pressurized pipelines with soilstructure interaction[J].Journal of the Brazilian Society of Mechanical Sciences and Engineering,2003,25(2):164-169.
[18]Kerr A D.On the stability of the railroad track in the vertical plane[J].Rail Int.,1974,5:131-142.
[19]Kerr A D.Lateral buckling of railroad tracks due to constrained thermal expansion[M].Railroad Track Mechanics and Technology,Pergamon Press,Oxford,1978.
[20]Taylor N,Gan A B.Submarine pipeline buckling imperfection studies[J].Thin-Walled Structures,1986,4:295-323.
[21]Boer S,Hulsbergen C H,Richards D M,et al.Buckling considerations in the design of the gravel cover for a high temperature oil line[C]//Proc.18th OTC,1986,May,5294.Houston,Texas,1986:1-8.
[22]Friedmann Y.Some aspects of the design of hot buried pipelines[C]//Offshore Oil and Gas Line Technology Conference,1986.Paris,France,1986:1-34.
[23]Richards D M,Andronicou A.Seabed irregularity effects on the buckling of heated submarine pipelines[C]//WEMT Advances in Offshore Technology.Amsterdam,1986:250-265.
[24]Ju G T,Kyriakides S.Thermal buckling of offshore pipelines[J].Journal of Offshore Mechanics and Arctic Engineering,1988,110(4):355-364.
[25]Pedersen P T,Jensen J J.Upheaval creep of buried heated pipelines with initial imperfections[J].Marine Structures,1988,1:11-22.
GAO Xi-feng1,LIU Run1,DU Zun-feng1,TAN Zhen-dong2
(1 State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China;2 Military Transportation Institute of the General Logistics Department,Tianjin 300161,China)
海底埋设管线屈曲剧变理论研究综述
高喜峰1,刘 润1,杜尊峰1,谭振东2
(1天津大学 水利工程仿真与安全国家重点实验室,天津300072;2总后军事交通运输研究所,天津300161)
海上生产的烃类必须在高温高压下运输以使流体舒缓而避免蜡组分的凝固。由于内外压差和温差引起强制膨胀导致轴向压缩力,此时便产生了海底管线的屈曲。此压缩力既能引起管线在海床平面内的侧向屈曲,也能造成垂向屈曲。通常将管线埋于沟槽内从而确保与其它海洋活动的干扰最小化。在此情况下,侧向土约束超过了由管线浮重造成的垂向隆起约束。因此,要特别注意挖沟埋设管线的垂向屈曲。最近对中国高温管线和渤海湾几起事故的关注引发中国海洋工程师对此现象的强烈兴趣。文章综述了海底埋设管线垂向屈曲的理论研究历史,以及作者对此问题的一些经验。希望海洋工程师能从本领域的文献综述和总结中受益。文中同时研究了管线的防护层设计,最后明确了未来发展的方向。
海底管线;沟槽;埋设;屈曲剧变
TE973
A
高喜峰(1975-),男,博士,天津大学建筑工程学院讲师;
谭振东(1979-),男,博士,总后勤部军事交通运输研究所高级工程师。
TE973
A
1007-7294(2011)06-0678-10
date:2011-04-27
Supported by China National Natural Science Foundation(No.40776055)and foundation of State Key Laboratory of Ocean Engineering(1002)
刘 润(1974-),女,博士,天津大学建筑工程学院教授;
杜尊峰(1984-),男,博士,天津大学建筑工程学院讲师;
- 船舶力学的其它文章
- Numerical Simulations of the Damage Process of Double Cylindrical Shell Structure Subjected to an Impact
- Finite Element Analysis of Delamination Initiation and Growth in E-Glass/Epoxy Reinforced Laminated Beams under Axial Impact
- Comparative Studies of the Transverse Structure Design Wave Loads for a Trimaran by Model Tests and Rule Calculations
- Numerical Simulation on the Process of Supercavity Development and the Planing State of Supercavitating Vehicle

