ANSYS索结构找形及悬链线的模拟
杨 钦 李承铭
(上海现代建筑设计(集团)有限公司)
ANSYS索结构找形及悬链线的模拟
杨 钦 李承铭
(上海现代建筑设计(集团)有限公司)
索结构的形态确定是一个非线性大位移问题。由于索结构的形状确定和预应力分布是一对相互影响的参数,因此,其工作阶段的几何状态一般是难以事先确定的,必须通过找形来确定。本文总结出了利用ANSYS对索结构进行找形的步骤,并通过计算实例,验证了ANSYS程序找形计算的准确性。对于比较长的单索,例如斜拉桥、悬索桥、索道等,具有很强的几何非线性,其垂度的影响是不可忽略的。然而,ANSYS软件单元库不包括曲线索单元,利用二节点直杆单元来模拟索单元仅在索长度不太大的情况下满足要求。基于此,本文提出了采用多段link10单元来模拟悬链线索单元。最后通过算例模拟悬链线索单元,验证由多段link10单元模拟悬链线索单元计算方法的可行性和准确性。
索单元;非线性;找形;悬链线
1 引言
索作为一种轻质、高效、大跨和经济的构件,在结构工程中扮演着非常重要的角色,如在索道、塔桅结构、悬索结构、斜拉结构、索桁结构、索穹顶及索膜结构中。在许多文献中已对多种索构件索的计算方法进行了研究,目前,索的模拟和分析方法已经成熟。与传统结构计算相比,索结构的初始形态和初始预应力分布是一对相互影响的未知量,这就产生了两个不确定量,也就是说既要形成假设的初始几何形态,又要满足初始假设的预应力分布,这用传统的结构力学方法是难以完成的,只能采用迭代法,通过几何形状和预应力分布的逼近来实现。现在常用的力密度法、动力松弛法、非线性有限元法均是通过迭代计算实现这一点。本文通过有限元软件ANSYS对索结构进行找形分析,总结出索结构进行找形步骤,并通过计算实例,验证ANSYS程序找形计算的准确性。对于比较长的单索,例如斜拉桥、悬索桥、索道等,是大变形柔性结构,其受力分析属于几何非线性问题,主要表现为:在几何上为大变形,具有很强的几何非线性;每根拉索的索长较大,其自重垂度不容忽略。针对拉索结构这些特点,必须选择正确的有限元模型对其进行非线性分析。关于斜拉索受力模型,使用索单元最方便的方法是采用包括非线性分析的通用有限元软件(例如ANSYS)进行计算。然而,软件的单元库不包括曲线索单元。许多学者都在使用link8或link10这两种杆单元模拟拉索的静动力特性,但利用二节点直杆单元来模拟索单元仅在索长度不太大的情况下满足要求。随着索跨度的不断增长,垂度的影响越来越不容忽视,这种单元将不再满足要求。本文利用已知的索端张力或预应力状态时的索长来求解索的原长[1],从而能够建立悬链线索单元的有限元模型。根据求解出的索原长,建立由多段link10单元组成的悬链线索单元模型。通过算例计算结果表明采用多段link10单元模拟悬链线索单元精度高,可应用于工程实践。
2 索结构基本假设和找形步骤
2.1 索结构基本假设ANSYS的实现
有限元分析理论把索看成是由一系列相互连接的索段组成,索段之间以节点相连。因此进行索结构有限元分析时,采用基于离散理论的节点位移法。这种方法以节点位移作为基本未知量,而以节点之间的索段为基本单元。
索的基本假设:
(1)索是理想柔性的,即不能承受任何弯矩,也不能受压;
(2)索的受拉工作符合胡克定律;
(3)荷载均作用在节点上,各索段均呈直线型。
ANSYS的实现:
(1)对于只能受拉,不能受压,受压时构件丧失刚度的柔性拉索。ANSYS提供了几类单元供选用,经过比较,本文采用link10空间单元来模拟。该单元设置了一个拉、压开关,打开受拉开关时,只需在单元初始实常数输入时定义面积和初应变,单元的特性就类似于受拉刚性杆件,刚度由截面积和弹性模量确定;一旦受压,即单元内出现反号应力,刚度随即丧失,单元退出工作。
(2)通过拉索的ANSYS单元选定,自然就满足单元只能承受轴向力而不能承受弯矩和剪力的假设。
(3)对于拉索的材料特性需符合应力—应变的胡克定律的假设,我们只需使分析过程在材料线性的条件下进行就可实现。
(4)针对结构上的分布荷载转化为节点上的等效荷载的假定,ANSYS在计算过程中可实现。
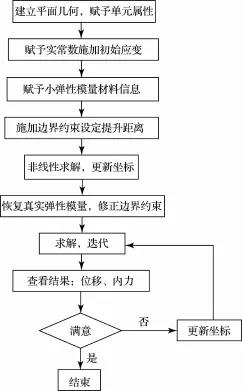
图1 找形流程图
2.2 ANSYS找形步骤
索采用只拉单元link10进行模拟,迭代采用NEWTON-RAPHSON方法,同时打开几何非线性及应力刚度选项。但是利用ANSYS进行索结构的找形分析时,为了有更好的收敛性,往往采用一种叫“小弹性模量”的方法。即在找形阶段把索材料的弹性模量缩小到一定的量级(1.0E-3),等找形结束后的荷载分析阶段,再把索的弹性模量恢复至真实值。
找形过程见图1。
3 预应力索原长的求解
3.1 基本假定
(1)索为理想柔索,不受压且无弯曲刚度;(2)满足大变形、小应变要求;
(3)索中的外荷载沿索长均匀分布。
3.2 刚度矩阵的建立
任一索元,各参数如图2所示。
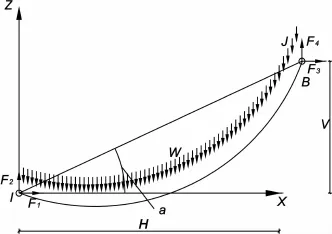
图2 悬链线索单元

其中,F1、F2为索元I节点处在局部坐标中的张力分量;F3、F4为索元J节点处在局部坐标中的张力分量;Ti、Tj为两节点处的索端张力值;Lu为索原长,L为索变形后的长度;H、V的定义如图1所示,W为索内沿索长均布竖向荷载(包括自重),A为索截面面积。由上面的表达式可知,一旦知道F1、F2、W和索原长Lu,就能求得V、H或者知道V、H、W和索原长Lu,就能求得F1、F2、F3和F4。Jayaraman根据上述方程详细推导了悬链线索元的刚度矩阵显式表达式并建立了已知索原长Lu迭代求解刚阵的方法。由于计算刚度矩阵时需要索原长Lu,因此必须根据节点位置和预张力值计算出索原长Lu。许多文献如文献[2]提出的基于线性搜索的迭代方法,文献[3]提出的采用Ridders改进弦割法迭代技术求解原长法,前提都是假定:

3.3 索原长高精度计算方法
文献【1】中考虑以下的简便近似计算方法:
式(1)是索考虑弹性变形以后的索长,而索无应力长度应为:

ΔL为索在张力作用下的弹性伸长量
假定索的张力为T(T=(Ti+Tj)/2),则在小应变情况下可以近似认为:

把式(13)代入式(12)得

把式(1)代入上式得
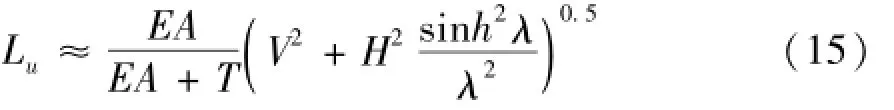
可以看出式(15)在索张力、索两端位置已知的情况下可以直接代入求解,避免了迭代。
4 ANSYS悬链线索单元模拟
link10单元双线性刚度矩阵特性使其成为一个轴向仅受拉或仅受压杆单元。使用只拉选项时,如果单元受压,刚度就消失,以此来模拟索的松弛或链条的松弛。这一特性对于用来模拟拉索受力问题非常有用。本文利用已知的索端张力或预应力状态时的索长先求解出索的原长,再根据求解出的索原长,建立由多段link10单元组成的悬链线索单元模型。步骤如下:
(1)先求解悬链线索两端点之间的索原长l,根据精度需要把索原长分成n段,每段均用一个link10单元来模拟,单元长度为l/n;
(2)在索两端点之间用由n个link10单元组成的索单元连接起来;
(3)在自重作用下求解得到悬链线索单元模型。
5 算例
例1:以支撑在刚性边界上的菱形索网结构为例[4],如图3所示,平面尺寸为73.2m×73.2m,屋面节点集中荷载2kN,平衡位置的坐标曲线为:z=3.66*(x/36.6)^2-36.6*(y/36.6)^2。索内力T=800kN,EA=293600kN。
在进行索网的找形计算时,以平面位置作为起始状态。设定拉索预拉力800kN,提升周边控制点到设计位置,控制点位置见表1(由于对称仅列出1/2的控制点)。在此过程中为了便于收敛将索的弹性模量降低两个数量级,把初始应变设为一个接近于1的量就可以得到最终的平衡位形。注意在找形过程中一定要控制索初始预拉力为假定的初始预拉力。最后得到的索网形状如图4所示。
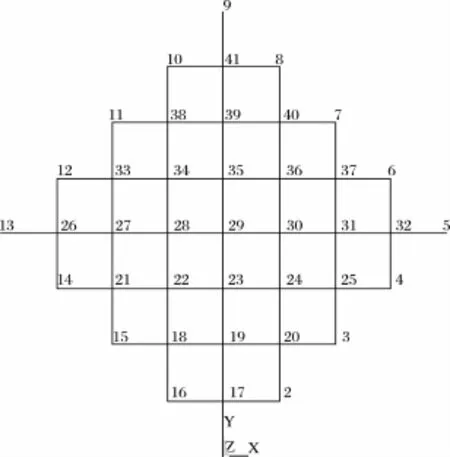
图3 菱形索网算例

表1 周边控制点提升后的坐标位置

表2 不同找形方法节点坐标比较(m)

图4 找形后菱形索网
表2列出找形计算结果的节点坐标值,由于菱形索网为对称结构,因此表中只列出了1/4平面的结果,节点编号如图3所示。
从表2的计算结果与文献[4]计算结果可以看出,本文得到的平衡曲面与理论值几乎一样,与五节点等参元计算结果比较,最大误差不到0.15%,与动力松弛法计算结果比较,最大误差仅为5.2%。这说明,用ANSYS对索结构进行找形分析精度非常高,同时还能大大提高计算效率。
例2:以铜陵长江公路大桥的某根索为例[5],该索水平投影长度为210.925m,竖直投影长度为110.485m,单位长度的质量为79.75kg/m。本文以索原长为已知值,建立由多段link10单元组成的悬链线索单元模型,求其它状态值。计算结果与文献[5]比较,结果如表3所示。

表3 算例2计算结果比较
从表3计算结果的对比可以看出,本文采用由多段link10单元组成的悬链线索单元的计算精度高,与文献[5]相比,塔端拉力的误差仅为0.12%,梁端竖向力的误差也仅为2.93%,而且建模方便快捷,可应用于工程实践。
例3:以宜宾小南门金沙江大桥施工用缆索吊装系统为例[6],如图5所示。两个塔架顶上各有一个定滑轮,施工中滑轮可在主索上滑动。节点的坐标I(0,0),KL(160,70),KR(460,70),J(620,0)。主索采用4根φ47.5的钢丝绳,面积为33.74cm2,单位长度重量为31.716kg/m,弹性模量取75.6GPa。设计起吊重量40吨,其中吊具重6吨。跨中索原长为649.989 3m,边跨索原长为174.382 8m,地锚处索力295kN。
塔架可用杆单元模拟,索段可用本文提出的多段link10单元模拟悬链线索单元。其中KL和KR与两个塔架之间用接触单元contact52模拟,设置contact52中实常数项START=2,摩擦系数为零来模拟滑轮。ANSYS模型如图6所示。
计算结果如图7和表4所示。

图5 塔架顶有滑轮的缆索吊装系统
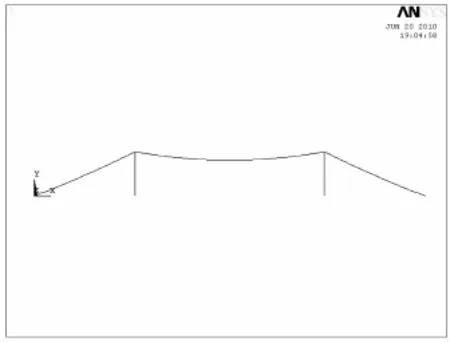
图6 ANSYS悬链线模型

表4 算例3计算结果比较

图7 计算结果
从表4计算结果的对比可以看出,本文的最大张力与设计值相差6.1%;最大垂度设计值的相差0.69%,而文献[6]中算例的计算结果最大张力与设计值相差8.2%;最大垂度与设计值的相差5.6%。因此本文的计算结果与设计值更为接近,结果令人满意,同时也验证了由多段link10单元模拟悬链线索单元计算方法的可行性和准确性。
6 结论
本文总结出了利用ANSYS对索结构进行找形的步骤,并通过计算实例,验证了ANSYS程序找形计算的准确性。同时,本文提出了采用多段link10单元来模拟悬链线索单元的方法。通过算例1验证了ANSYS对索结构进行找形分析精度高,同时还能大大提高计算效率。算例2和算例3验证了由多段link10单元组成的悬链线索单元计算方法的可行性和准确性,而且建模方便快捷,可应用于工程实践。
[1]汤荣伟,沈祖炎,赵宪忠,苏慈.预应力索原长直接求解方法.空间结构,2004,10(4):16-17.
[2]向景武,罗绍湘,陈鸿天.悬索结构振动分析的悬链线索元法.工程力学,1999,16(3):130-134.
[3]张立新,沈祖炎.预应力索结构中的索单元数值模型.空间结构,2000,6(2):18-23.
[4]余志祥.索网结构非线性全过程分析与研究.西南交通大学学位论文,2003:28-37,69-73,74-75.
[5]杨佑发,白文轩,郜建人.悬链线解答在斜拉索数值分析中的应用.重庆建筑大学学报,2007,29(6):31-34.
[6]魏建东.索结构分析的滑移索单元法.工程力学,2004,21(6).
ANSYS Form Finding and Catenary Simulation of Cable Structure
Yang Qin,Li Chengming
(Shanghai Xian Dai Architectural Design Group,Shanghai200041,China)
How to decide the form of cable structure is the issue of great nonlinear displacement.The form of cable structure and the distribution of pre-stress are both parameters which influence each other,so its working geometrical state is difficult to decide beforehand,the way to make sure is form finding.This paper is about how to use ANSYS for form finding of cable structure and the steps have been concluded,some account cases also been given to verify the accuracy of ANSYS calculation program for form finding.For the long single cable,such as cablestayed bridge,suspension bridge and cableway which have gecometric nonlinearity,its verticality can not be ignore.However,ANSYS element library don't include cable element,only when cable isn't long can we use link10 to simulate cable.Based on this,this paper proposes a multi-segment link10 unit to simulate the catenary unit.At the end,an account case which used to stimulate catenary is given to verify that it is feasible and accurate enough to use several link10 to stimulate catenary as computational method.
Cable Element;Nonlinearity;Form Finding;Catenary
TU351
A
1674-7461(2010)04-0061-05
杨 钦(1984-),男,工学硕士,结构工程师。从事结构工程方面的研究。E-mail:qin_yang@xd-ad.com.cn;李承铭(1963-),男,工学博士,副教授。从事结构工程方面的研究。E-mail:chengming-li@xd-ad.com.cn

