离散猴群算法及其在输电网扩展规划中的应用
王靖然,余贻鑫,曾 沅
离散猴群算法及其在输电网扩展规划中的应用
王靖然,余贻鑫,曾 沅
(天津大学智能电网教育部重点实验室,天津 300072)
猴群算法(MA)是一种只适于求解连续变量优化问题的群智能算法. 针对MA的局限并结合输电网扩展规划问题的特点,设计了能够求解含有离散变量优化问题的离散猴群算法(DMA). 算法中提出的大、小2种爬过程解决了原猴群算法求解离散优化问题时爬过程失效的问题,合作过程和随机扰动机制的引入也提高了算法的计算效率. 算例结果表明,DMA计算速度快,鲁棒性强,用很小的猴群规模就能够对不同维数的输电网扩展规划问题均达到很好的计算效果.
输电网扩展规划;离散猴群算法;爬过程;进化计算;群智能
输电网扩展规划问题在数学上是一个大规模的组合优化问题.目前,其求解技术主要包括3类:数学优化方法、启发式方法和现代启发式方法[1].虽然经典的数学优化方法能够从理论上保证解的最优性,但在求解较大规模的问题时往往需要相当长的计算时间[2].而启发式方法在求解大规模问题时更难以保证解的质量[3].
近年来,现代启发式方法由于实现简单、不受搜索空间和目标函数形态的制约而得到了广泛的应用.文献[4-7]将遗传算法应用于求解输电网扩展规划问题,取得了不错的效果.文献[8]采用了一种新的离散化粒子群方法求解该问题.文献[9-10]分别对粒子群算法进行改进以提高算法的全局收敛能力.此外,模拟退火算法[11]、禁忌搜索算法[12]以及蚁群算法[13]等也都在求解输电网扩展规划问题中得到了应用.但这类算法在求解大规模问题时必须具有较大的(种)群规模,而这会导致更长的计算时间;如果种群规模过小,则极易陷入局部最优.
猴群算法(monkey algorithm,MA)是一种适于求解大规模优化问题的群智能算法,但只能够求解含连续变量的优化问题.笔者根据输电网扩展规划问题的特点,改进了猴群算法的爬过程,并引入合作过程和随机扰动机制,设计了能够求解含有离散变量优化问题的离散猴群算法.将该算法应用于求解目标年输电网扩展规划问题,算例的对比结果表明了其实用性和有效性.
1 猴群算法基本原理
猴群算法是模拟猴子的爬山过程而设计的群优化算法,适合于求解多变量、多峰函数的优化问题[14].算法在问题的求解过程中,利用目标函数在当前解处的伪梯度信息,通过猴群中每只猴子的爬过程、当前解邻域内的望-跳过程以及各猴子的翻过程,不断搜索解空间的各个区域直至找到问题的全局最优解.
猴群算法的优点体现在:①不要求目标函数连续或可微,线性或非线性的问题均可求解;②算法实现简单,需要调整的参数较少;③能够求解维数较高的优化问题,且猴群规模对问题的维数不敏感.但该算法只适于求解连续变量的优化问题,而对含有离散变量的优化问题,伪梯度不能总是给出下降的搜索方向,从而导致爬过程失效,算法无法求解.
2 求解输电网扩展规划问题的离散猴群算法
2.1 输电网扩展规划问题的数学模型
对规划水平年确定的电源规划方案和负荷水平,满足静态安全性约束的目标年输电网扩展规划模型为
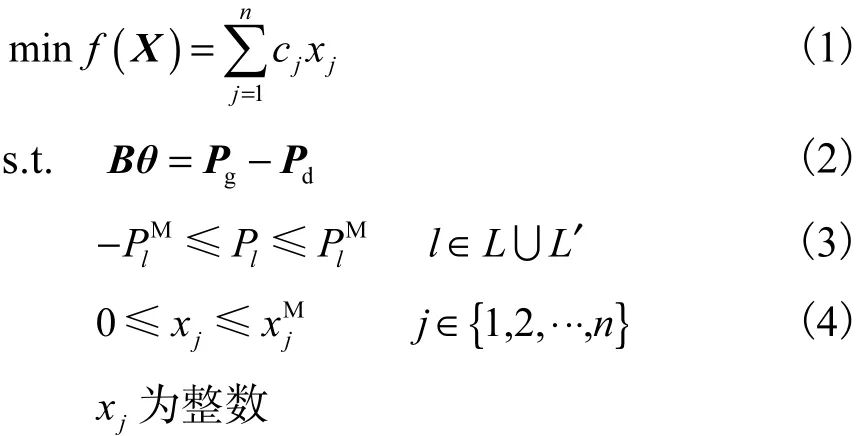
式中:X=(x1,x2,···,xn)T;xj为第j条可扩建输电走廊上新建的线路数量;xMj为其上限;cj为建设1条线路的投资成本;n为系统可扩建输电走廊数;B为系统电纳矩阵;θ为节点电压相角向量;Pg和Pd分别为节点有功发电出力和有功负荷列向量;Pl为支路l的有功潮流;PlM为支路l最大容许传输功率;L和L′分别为系统原有支路和新建支路的集合.整个模型求解的是在满足节点功率平衡约束式(2)、支路潮流约束式(3)和架线数量约束式(4)的条件下投资最小的规划方案.
2.2离散猴群算法
第2.1节中的输电网扩展规划模型是一个含有离散变量的组合优化问题,难以用原有的猴群算法求解.为此设计离散猴群算法(discrete MA,DMA)如下.
1)解的表述
设猴群的规模为M,对猴群中的第i只猴子,其当前位置定义为

式中Xi的各分量对应于系统可扩建的输电走廊,每一分量上的值xi,1,xi,2,···,xi,n表示相应输电走廊上的架线数.这样每只猴子的当前位置对应于一个候选规划方案.
2)目标函数的修正
电网规划中常常需要将孤立的发电、负荷节点或孤立的小系统连入已有系统,而随机产生的规划方案往往难以满足连通性或线路传输功率限值要求,因此将网络连通性和支路有功潮流约束式(3)以惩罚项的形式加入目标函数,修正的目标函数为
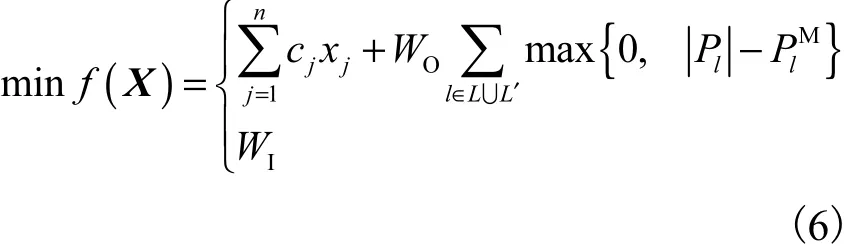
式中:OW为网络连通但出现支路过负荷时的惩罚系数;IW为网络不连通时的惩罚值.
3)爬过程
设第i只猴子的当前位置为Xi=(xi,1,xi,2, ···,x)T,i∈{1,2,··,M}.爬过程可分为2种,大步爬i,n
过程和小步爬过程.
(1)大步爬过程步骤如下.
步骤1 随机产生向量ΔX=(Δx,Δx,···,Δx)T,ii,1i,2i,n其中Δxi,j为从区间[−aL,aL]中随机产生的整数,j∈{1,2,··,n}.aL称为大步爬过程的步长.
步骤2 计算f(Xi+ΔXi)和f(Xi−ΔXi).
步骤3 如果f (Xi+ΔXi)<f(Xi−ΔXi)且f(Xi+ ΔXi)<f (Xi),则令Xi=Xi+ΔXi;
如果f (Xi−ΔXi)<f (Xi+ΔXi)且f(Xi−ΔXi)<f(Xi),则令Xi=Xi−ΔXi.
步骤4 重复步骤1~步骤3,直到目标函数值不再发生变化或达到预先设定的次数C,LN.
(2)小步爬过程步骤如下.
步骤1 依次随机产生向量ΔXi=(0,···,0,Δxi,j, 0,···,0)T,j∈{1,2,··,n},其中Δx为从区间[−a,a]中
i,jSS随机产生的非零整数.aS称为小步爬过程的步长.
步骤2 计算f(Xi+ΔXi)和f(Xi−ΔXi).
步骤3 如果f (Xi+ΔXi)<f(Xi−ΔXi)且f(Xi+ ΔXi)<f (Xi),则令Xi=Xi+ΔXi;
如果f (Xi−ΔXi)<f (Xi+ΔXi),且f(Xi−ΔXi)<f(Xi),则令Xi=Xi−ΔXi.
步骤4 重复步骤1~步骤3,直到目标函数值不再发生变化或达到预先设定的次数C,SN.
4)望-跳过程
经过爬过程,每只猴子都达到了各自较优的位置,在此位置上,每只猴子都在一定的视野范围内向周围眺望,如果发现了更好的位置(更优的解),则跳向那个位置,进而重复爬过程.对于第i只猴子,i∈{1,2,··,M},望-跳过程的计算步骤如下.
步骤2 如果f(Xi′ )<f(Xi),则令Xi=Xi′.
步骤3 重复步骤1和步骤2,直至达到预先设定的次数WN.
5)合作过程
在爬过程和望-跳过程之后,每只猴子都到达了其邻域内的较优位置,但各猴子的位置必然存在优劣的差异.合作过程就是让爬山能力强、处于较优位置的猴子与处于较差位置的猴子合作,以共同找到更好的解.
设本代中出现的最优猴子的位置为X∗=,,···,)T,对于第i只猴子的当前位置,合作过程的步骤如下.
步骤1 在[0,1]内随机产生实数α.
步骤3 令Xi=重复爬过程.
合作过程能够显著增强算法的寻优能力,增加找到的解的多样性.
6)翻过程
翻过程的目的是使猴群能够探索新的搜索区域,其步骤如下.
步骤1 在[c,d]区间内随机产生实数β.
步骤3 对∀i∈{1,2,··,M},∀j∈{1,2,··,n}计算
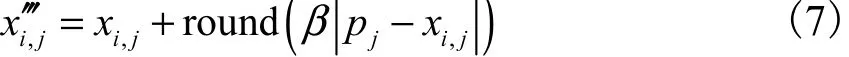
步骤4 令Xi=,重复爬过程.
在步骤1中,区间[c,d]称为翻区间,决定了猴子从当前位置能够翻至的最大距离.如果猴子的新位置大于其上限,则令=;如果小于0,则令=0.
7)随机扰动机制
在翻过程中,当所有猴子的第j位xi,j均相同时,由式(7)可知,此时=xi,j,翻过程将失去作用.为此,引入随机扰动机制:随机选取猴群中的某只猴子k∈{1,2,··,M},令中随机产生的均匀分布的整数,且e不等于xi,j的原值,之后再进行猴群的翻过程.
随机扰动机制的引入增加了猴群的多样性,使搜索过程避免陷入局部最优.
8)终止准则
与通常的智能算法相似,DMA可以有两种终止准则:
(1)当达到预先设定的搜索代数时计算终止;(2)当所找到的最优解连续K代不发生变化时计算终止.
为了减少额外的计算时间,采用第2种终止准则,其中K的取值应根据问题规模的大小确定.
2.3离散猴群算法的计算流程
求解目标年输电网扩展规划问题的离散猴群算法计算流程如图1所示.
在图1中,猴群经过爬过程、望-跳过程、合作过程和翻过程之后完成了一次搜索过程,称之为一代.问题的最优解可能出现在搜索过程中的任何一代,算法也不存在所有猴子都收敛的说法.
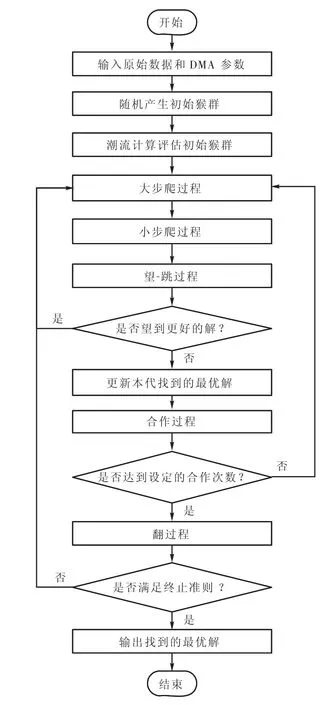
图1 离散猴群算法计算流程Fig.1 Flow chart for DMA
3 算例分析
3.118节点系统
18节点系统的简化网络接线图如图2所示,虚线表示可扩建线路走廊,实线表示已有线路.系统原始参数见文献[15],所求问题的规模为21维.采用Matlab编程,取猴群规模M=5,爬过程的步长aL=1,aS=1,次数NC,L=7,NC,S=4,眺望视野b=1,翻区间为[−20,20].随机产生初始猴群,每代4次合作,经过50次测试计算的结果如表1所示,表中同时列出了原始猴群算法(primary MA,PMA)、加入模拟退火机制的改进遗传算法(improved genetic algorithm,IGA)和惯性权重随代数逐渐下降的离散粒子群算法(discrete particle swarm optimization, DPSO)的计算结果,其中原始猴群算法是指严格按照文献[14]的计算流程且将所涉及到的变量全部整数化的猴群算法.

图2 18节点系统简化网络接线Fig.2 Simplified network connection for 18-bus system
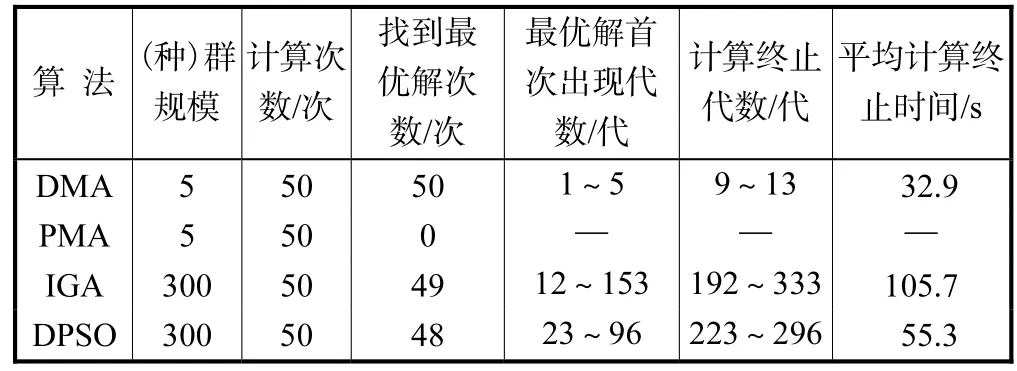
表1 DMA与PMA、IGA和DPSO算法计算18节点系统的比较Tab.1 Comparison among DMA,PMA,IGA and DPSO in 18-bus system
从表1中可以看到,对于18节点系统,由于此时问题的规模较大,未经改进的原始爬过程失效,PMA完全找不到最优解.而DMA仅需要5只猴子在5代之内就能找到最优解,50次计算中有25次在第1代就找到了最优解,其首次出现的平均代数为1.9代,从开始到计算终止的平均计算时间为32.9 s.DPSO和IGA算法需要用300个粒子或个体才能达到接近100%的收敛率,计算时间也较DMA长.计算中还发现,DMA能够找到2个投资成本相同的最优解:1-111x=,4-161x=,5-121x=,6-131x=(或7-131x=),6-142x=,7-81x=,8-91x=,9-102x=,14-151x=,16-172x=,17-181x=,有时这2个最优解甚至在同一代内出现,这说明DMA不但具有很强的寻优能力,而且找到的解具有很强的多样性.
表2为猴群规模取不同值时DMA的计算结果.可以看到,随着猴群规模的减小,每代的计算时间相应减小,而最优解首次出现的代数有所增加.但即使只有2只猴子,DMA也能够以100%的概率找到最优解.经对比可知,当猴群规模为4~6时,算法均能达到满意的计算效果.
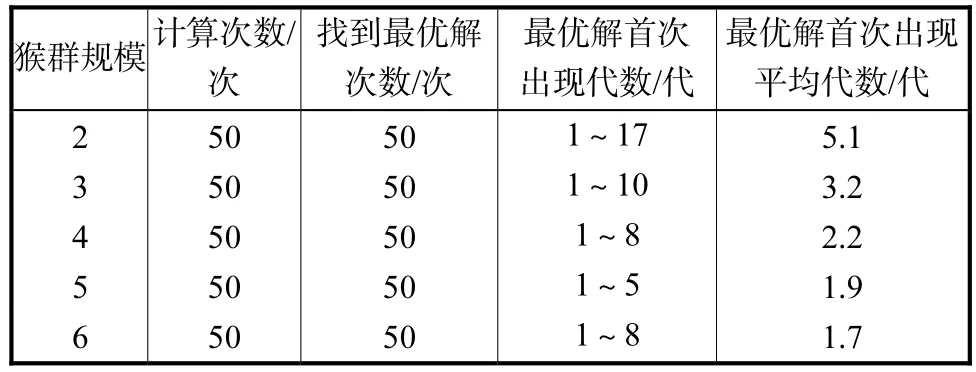
表2 猴群规模对DMA寻优能力的影响Tab.2 Effect of population size of monkeys on computational capability of DMA
3.2IEEE 24节点系统
IEEE 24节点系统共有41条可扩建线路走廊,网络结构和原始参数见文献[16-17].表3列出了DMA与IGA、DPSO算法的对比结果.其中,DMA的参数设置如下:猴群规模5M=,爬过程的步长aL=1,aS=1,次数NC,L=8,NC,S=4,眺望视野b=1,翻区间为[−20,20],每代4次合作.
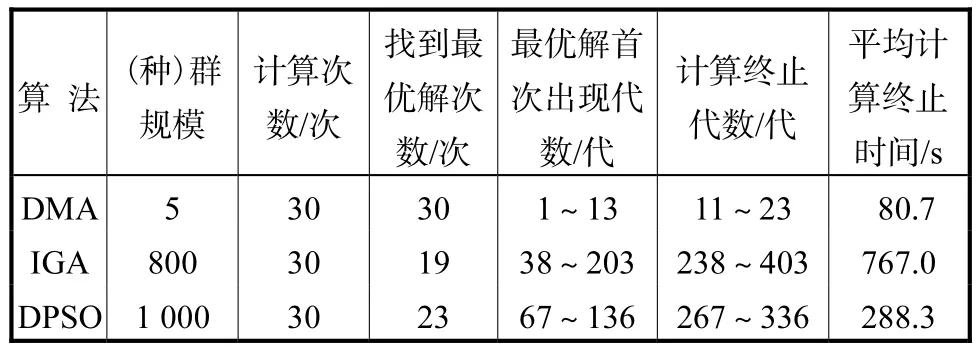
表3 DMA与IGA、DPSO算法计算24节点系统的比较Tab.3 Comparison among DMA,IGA and DPSO in 24-bus system
当所求解系统的规模增加到41维时,IGA和DPSO算法需要的(种)群规模和计算时间均显著增加,且难以达到100%的收敛率;而DMA仍然只需要5只猴子就能以100%的概率找到最优解:6-101x=,7-82x=,10-121x=,14-161x=,16-171x=,20-231x=,其平均计算终止时间仅为80.7 s.由此可见,当系统的规模增加时,DMA仍具有很强的寻优能力,相比之下的优越性也更为明显.
表4示出了合作过程对DMA寻优能力的影响.从表4中可见,当没有合作过程时,算法虽然也能以100%的概率找到最优解,但最优解首次出现的代数显著增加.这说明合作过程能够显著提高DMA的搜索能力,加快寻优过程.
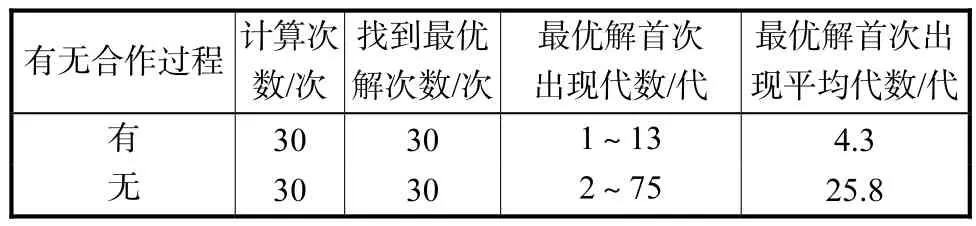
表4 合作过程对DMA寻优能力的影响Tab.4 Effect of cooperation process on computational capability of DMA
4 结 论
针对猴群算法只能求解连续变量优化问题的不足,结合输电网扩展规划问题的特点,本文从解的表述、目标函数的修正、爬过程、望-跳过程、合作过程、翻过程、随机扰动机制以及终止准则等方面设计了能够求解含有离散变量优化问题的离散猴群算法,解决了爬过程失效的问题.通过对18节点系统和IEEE 24节点系统的计算,结果表明:
(1)通常情况下,离散猴群算法仅需4~6只猴子就能够达到很好的计算效果;
(2)合作过程的引入显著增强算法的寻优能力;
(3)相对于遗传算法和离散粒子群算法,离散猴群算法计算速度快,鲁棒性强,尤其适于求解较大规模的优化问题.
本文中提出的仅是基本的离散猴群算法,具有一定的求解离散优化问题的通用性,如何与更高效的局部优化方法相结合以提高其计算效率,是需要进一步研究的工作.
[1] 段 刚,余贻鑫. 电力系统NP难问题全局优化算法的研究[J]. 电力系统自动化,2001,25(5):14-18.
Duan Gang,Yu Yixin. A study on global optimization for NP hard problems in power systems [J]. Automation of Electric Power Systems,2001,25(5):14-18(in Chinese).
[2] Latorre G,Cruz R D,Areiza J M,et al. Classification of publications and models on transmission expansion planning [J]. IEEE Transactions on Power Systems,2003,18(2):938-946.
[3] Romero R,Monticelli A,Garcia A,et al. Test systems and mathematical models for transmission network expansion planning [J]. IEE Proceedings:Generation,Transmission and Distribution,2002,149(1):27-36.
[4] 段 刚,余贻鑫. 输配电系统综合规划的全局优化算法[J]. 中国电机工程学报,2002,22(4):109-113.
Duan Gang,Yu Yixin. Giobal optimization for power transmission and distribution system planning[J]. Proceedings of the CSEE,2002,22(4):109-113(in Chinese).
[5] 王秀丽,王锡凡. 遗传算法在输电系统规划中的应用[J]. 西安交通大学学报,1995,29(8):1-9.
Wang Xiuli,Wang Xifan. Transmission system planning with genetic algorithm[J]. Journal of Xi’an JiaotongUniversity,1995,29(8):1-9(in Chinese).
[6] Gallego R A,Monticelli A,Romero R. Transmission system expansion planning by an extended genetic algorithm [J]. IEE Proceedings:Generation,Transmission and Distribution,1998,145(3):329-335.
[7] da Silva E L,Gil H A,Areiza J M. Transmission network expansion planning under an improved genetic algorithm[J]. IEEE Transactions on Power Systems,2000,15(3):1168-1175.
[8] Jin Yixiong,Cheng Haozhong,Yan Jianyong,et al. New discrete method for particle swarm optimization and its application in transmission network expansion planning[J]. Electric Power Systems Research,2007,77(3/4):227-233.
[9] 胡家声,郭创新,叶 彬,等. 离散粒子群优化算法在输电网络扩展规划中的应用[J]. 电力系统自动化,2004,28(20):31-36.
Hu Jiasheng,Guo Chuangxin,Ye Bin,et al. Application of discrete particle swarm optimization to transmission network expansion planning[J]. Automation of Electric Power Systems,2004,28(20):31-36(in Chinese).
[10] 金义雄,程浩忠,严健勇,等. 改进粒子群算法及其在输电网规划中的应用[J]. 中国电机工程学报,2005,25(4):46-50.
Jin Yixiong,Cheng Haozhong,Yan Jianyong,et al. Improved particle swarm optimization method and its application in power transmission network planning[J]. Proceedings of the CSEE,2005,25(4):46-50(in Chinese).
[11] Romero R,Gallego R A,Monticelli A. Transmission system expansion planning by simulated annealing[J]. IEEE Transactions on Power Systems,1996,11(1):364-369.
[12] da Silva E L,Ortiz J M A,de Oliveira G C,et al. Transmission network expansion planning under a tabu search approach[J]. IEEE Transactions on Power Systems,2001,16(1):62-68.
[13] 陈根军,王 磊,唐国庆. 基于蚁群最优的输电网络扩展规划[J]. 电网技术,2001,25(6):21-24.
Chen Genjun,Wang Lei,Tang Guoqing. An ant colony optimization method for transmission network expansion planning[J]. Power System Technology,2001,25(6):21-24(in Chinese).
[14] Zhao Ruiqing,Tang Wansheng. Monkey algorithm for global numerical optimization[J]. Journal of Uncertain Systems,2008,2(3):164-175.
[15] Wang Xifan,McDonald J R. Modern Power System Planning[M]. London:McGraw-Hill Publishing Company,1994.
[16] Reliability Test System Task Force of the Application of Probability Methods Subcommittee. IEEE Reliability Test System[J]. IEEE Transactions on Power Apparatus and Systems,1979,98(6):2047-2054.
[17] Fang Risheng,Hill D J. A new strategy for transmission expansion in competitive electricity markets[J]. IEEE Transactions on Power Systems,2003,18(1):374-380.
Discrete Monkey Algorithm and Its Application in Transmission Network Expansion Planning
WANG Jing-ran,YU Yi-xin,ZENG Yuan
(Key Laboratory of Smart Grid of Ministry of Education,Tianjin University,Tianjin 300072,China)
Monkey algorithm(MA)is a swarm intelligence algorithm only for optimization problems with continuous variables. In view of the limitations of MA and the features of transmission network expansion planning,discrete monkey algorithm(DMA)is proposed for optimization problems with discrete variables. Large-step and small-step climb processes were designed to tackle the problem of invalid climb process in discrete optimization with primary MA. Cooperation process and stochastic perturbation mechanism were also introduced to improve the computational efficiency of the proposed algorithm. The numerical results demonstrate that DMA has strong robustness and is capable of solving expansion planning problems of various dimensions efficiently and rapidly with small population size. Keywords:transmission network expansion planning;discrete monkey algorithm;climb process;evolutionary computation;swarm intelligence
TM715
A
0493-2137(2010)09-0798-06
2009-10-10;
2010-05-05.
“十一五”国家科技支撑计划重大资助项目(2008BAA13B01).
王靖然(1982— ),男,博士研究生,jrwang@tju.edu.cn.
余贻鑫,yixinyu@tju.edu.cn.

