基于OAT输入整形器和能量控制的不确定柔性航天器姿态跟踪
陈艳华
基于OAT输入整形器和能量控制的不确定柔性航天器姿态跟踪
陈艳华
(北京航空航天大学第七研究室,北京 100191)
针对含模型不确定性的柔性航天器姿态跟踪和振动抑制问题,提出了一种将最优任意时延(OAT)输入整形器和能量控制相结合的控制方法.其中前馈控制是根据系统标称模型参数设计的OAT输入整形控制,将其与参考输入指令做卷积后作用到标称模型上能够实现期望的姿态跟踪,且当反馈控制环节出现故障时能保证受控系统的基本安全性.考虑到标称模型与实际系统间的误差,采用基于对象能量的跟踪控制方案设计了反馈控制器,并证明了与前馈控制结合后闭环系统的稳定性.仿真结果验证了所提出方法的优越性.
OAT输入整形器;柔性航天器;姿态跟踪控制;基于能量的控制;振动抑制
在现代航天科学发展过程中,柔性化和低刚度是各类航天结构的一大特点,对这种柔性航天器的控制往往需要快速抑制其在姿态机动中所产生的残余振动.柔性航天器的振动控制在过去一段时间取得了很大的成功,研究者尝试使用各种主动控制方法进行振动控制,Rattan、Nathan和Siciliano等[1-3]分别运用自适应控制、变结构控制和奇异值扰动理论进行振动控制.为了提高控制系统的鲁棒性,Sundareshan等[4]考虑了基于神经元网络的变结构控制策略.而Tzes等[5]利用基于输入整形技术的自适应控制方法控制两杆柔性操作器,取得了较好的效果.
以上的柔性航天器振动控制方法可分为2类:反馈控制和前馈控制.反馈控制方法使用测量信号;而前馈控制方法仅使用期望的参考信号.输入整形技术是一种前馈方法,其基本思想是通过考虑系统的物理特性和振动特性,构造前馈振动控制方法,使得振动模态在系统的输入信号中不被激励,可以从根本上消除振动,而且不需要额外的传感器,应用十分方便.Smith[6]于1957年提出的Posticast控制方法可以看作是早期的输入整形技术.研究发现,这种控制方法对参数的变化很敏感,因此很长时间内输入整形技术的应用受到很大限制.直到1990年,Singer和Seering[7]第一次正式提出输入整形技术,将输入信号整形后对柔性体的残余振动进行控制,提出的输入整形器是将一系列脉冲与输入信号做卷积计算而得,给出了系统相对残余振动的数学表达式,并研究了典型的输入整形器,即零振动ZV整形器、零振动加微分ZVD整形器的设计方法和特性,同时指出通过对约束方程的连续微分,可以设计出更高阶的输入整形器.与ZV、ZVD输入整形器不同,Rhim和Book[8]利用最优化方法设计的OAT输入整形器,适用于可表示为线性常微分方程的振动模型,且允许整形器脉冲序列的幅值为负值.其鲁棒性优于ZV和ZVD.
然而在实际应用中,由于求取脉冲的幅值和作用时刻要求精确的数学模型,所以整形器对模型具有严重的依赖性,对于模型参数的变化很敏感,并且涉及到非线性优化计算,而其鲁棒性是令谐振频率处的偏微分方程等于零,没有考虑其他模型不确定性以及参数摄动和外界干扰的影响.因此,在实际应用中,通常将整形器和其他反馈控制配合使用.
葛树志提出的柔性结构基于能量的控制方法[9]是一种抑制振动的反馈控制方法,其设计只利用系统的基本能量关系,并不需要知道具体的系统模型信息,而且设计时基于反映柔性结构形变的偏微分方程,可以直接抑制振动.笔者针对柔性航天器姿态跟踪控制问题,提出了一种将OAT输入整形控制和中能量控制相结合的控制方法.其中作为前馈控制的OAT输入整形控制利用系统标称模型的模态参数设计,将其与期望的参考输入指令做卷积后作用到标称模型上能够完成期望的姿态机动;由于前馈控制是根据系统标称模型参数设计,所以当反馈控制回路出现问题时能够保证受控系统的稳定性和基本性能指标.而反馈控制是基于对象能量关系设计的一种只利用中心刚体姿态角、姿态角速度和形变测量数据,与具体模型参数无关的姿态跟踪控制方案[9],并证明了将前馈控制与反馈控制结合后闭环系统的稳定性.文中对所提出的控制方法进行了仿真研究,结果表明,这一方法是可行而有效的.与文献[9]中只利用能量控制的方案相比,将OAT输入整形器和能量控制方法相结合能得到更好的控制效果.
1 动力学模型
柔性航天器模型可抽象为图1所示的中心刚体加柔性杆模型,本节介绍利用扩展的哈密尔顿原理建立其动力学方程[9].选择相对参考系Oxy中x轴在原点处和柔性杆相切,这样x轴就可以被看作是柔性杆没有发生形变时的位置.不失一般性,首先给出以下假设:
(1)杆具有均匀的密度和弯曲刚度;
(2)和杆的长度相比,杆的形变量很小;
(3)不考虑阻力和重力的影响.
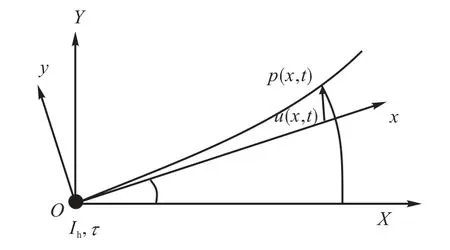
图1 柔性航天器模型Fig.1 Model of flexible spacecraft
一些基本参数:l为柔性航天器的长度;EI为柔性航天器的弯曲刚度;r为柔性航天器的密度;hI为轴心惯性力矩;()tτ为作用在基点处的力矩;()tθ为关节旋转角度;(,)uxt为相对于未形变时的弹性形变;(,)pxt为柔性航天器中某点的位置.
因柔性杆的形变(,)uxt很小,故杆中一点的位置可表示为

式中0xl≤≤总是成立,以后除特别说明,x均在此范围内.
系统的动能为
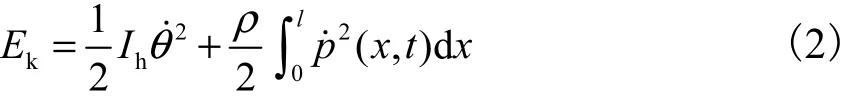
由前面的假设知,系统的势能pE仅来自于柔性杆的弯曲应变能量,即有
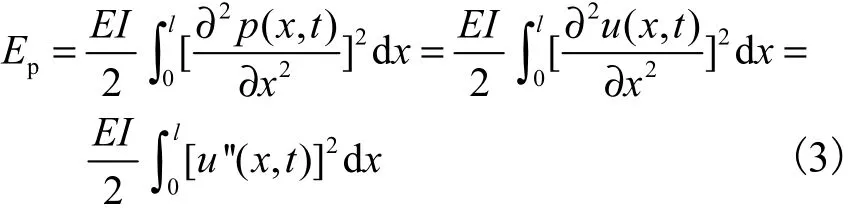
记力矩τ(t)所做的功W=τ(t)θ(t).根据扩展的哈密尔顿原理可得
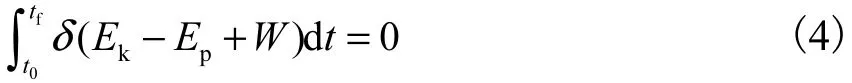
式中:0t为柔性航天器开始运动的时间;ft为柔性航天器运动停止的时间.将式(2)和式(3)代入式(4),就可以获得系统方程为
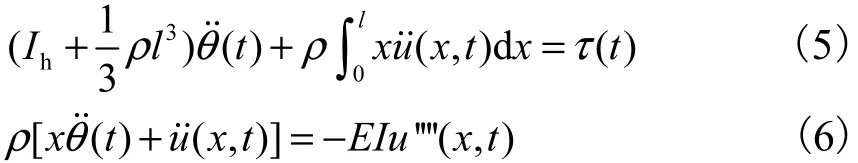
式中点号和撇号分别表示对t和x求导.其中式(5)为中心刚体的力矩平衡方程,式(6)为柔性杆振动的偏微分方程.对应的边值条件为
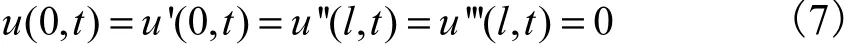
要研究的问题是:考虑由式(5)和式(6)描述的柔性航天器动力学模型,由初始状态
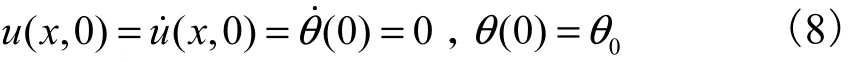
出发,如何设计控制力矩()tτ,使得中心刚体姿态沿参考轨迹快速机动到0,同时抑制柔性杆的残余振动,即使
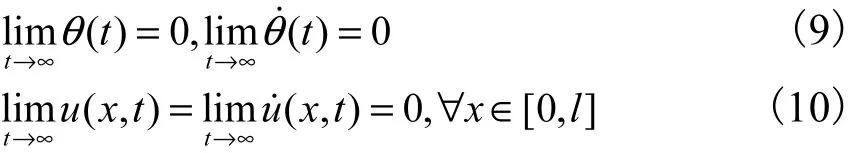
2 控制方案
控制方案如图2所示.先由实际对象参数的估计值得到标称模型,对中心刚体标称模型设计出可完成期望姿态机动的“梆-梆”控制律(参考指令)r,再利用标称模型中的振动模态设计OAT输入整形器,该整形器输出与参考指令r做卷积后得到的整形指令mu作用在标称模型上给出了期望的姿态机动参考轨迹mθ,作用在实际对象上能够保证在反馈环节出现问题时的基本安全性.最后基于系统的能量关系设计出反馈控制器,补偿实际对象和标称模型间的误差,使得最终所得的闭环系统能完成给定的姿态跟踪与振动抑制任务.
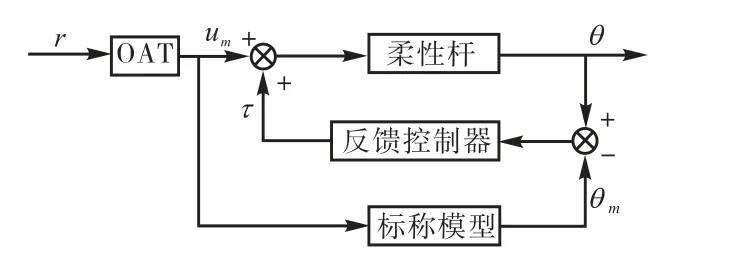
图2 控制方案示意Fig.2 Schematic of control project
3 规划期望轨迹
考虑针对式(5)和式(6)所示模型,在有限截断情况下[10],设计OAT输入整形器和输入指令,使得整形参考指令作用在标称模型上能够得到期望的参考轨迹.这里取含一个柔性模态的情况作为标称模型,即
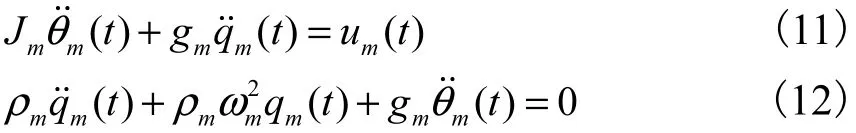
式中mJ、mg、mρ、2mω为已知参数;mθ和mq分别为标称模型的姿态角和模态坐标;mu为整形后的参考指令.由如图2所示的控制方案有

式中:*为卷积符号;f为OAT输入整形器方程.式(13)在频域中为

将标称式(11)和式(12)做拉普拉斯变换,可得姿态角、振动模态和输入指令之间的传递函数分别为
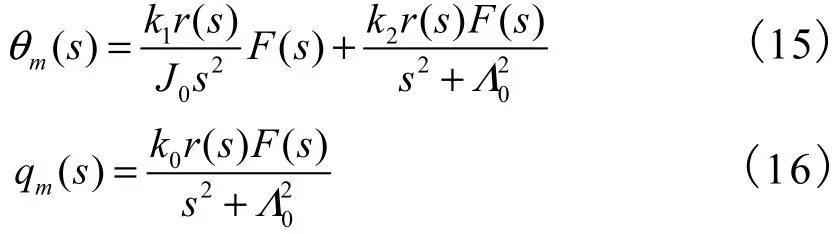
根据文献[8]设计OAT整形器为
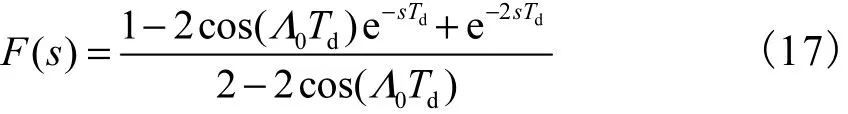
式中dT为时延.为了保证整形前后有相同的稳态响应,将OAT整形器的幅值规范化为单位DC增益.则OAT在频域中的零点为
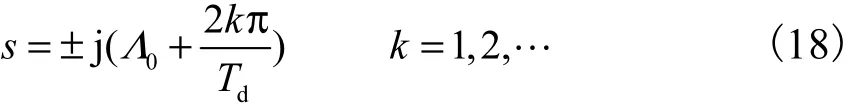
由式(17)和式(18)可以看出,OAT输入整形器的零点集覆盖了振动方程(16)的极点.因此不管时延dT值为多少,都能达到零-极点消除的结果,可以消除振动.由式(15)可知,姿态角mθ的运动也受振动模态的影响(即式(15)右端第2项),OAT输入整形器作用在式(15)上,可以消除该振动环节.又由式(15)右端第1项知,OAT输入整形器作用与否不影响系统的稳态响应.因此,只要针对中心刚体标称模型Jmθ˙m(t)=r(t )设计出“梆-梆”控制律,然后将其与式(17)做卷积,得到的整形指令作用在式(11)和式(12)所示标称系统上即可以完成期望的姿态机动,也可以消除残余振动.
要使中心刚体标称模型t=0时从初始状态(θm(0)=θ0,θ˙m(0)=0)出发到t=tf时达到期望状态(θm(tf)=0,θ˙m(tf)=0,tf为总的运动时间),若取作用在中心刚体上的参考输入指令r为常量,则可设计
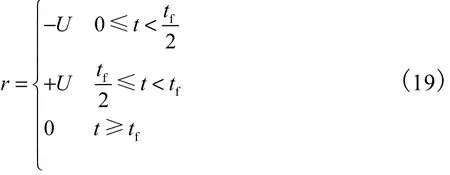
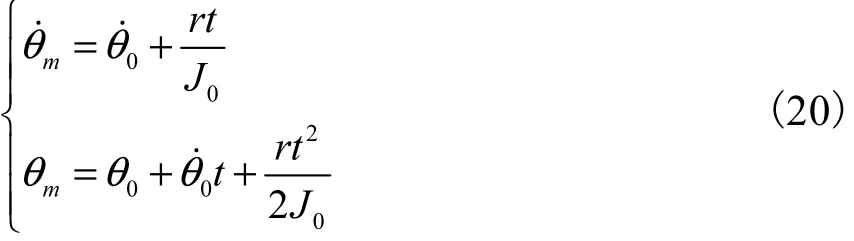
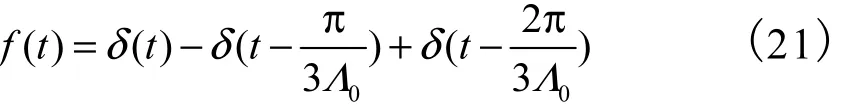
式中()tδ为单位脉冲.将OAT输入整形器和式(19)所示的参考输入指令做卷积可得整形输入为
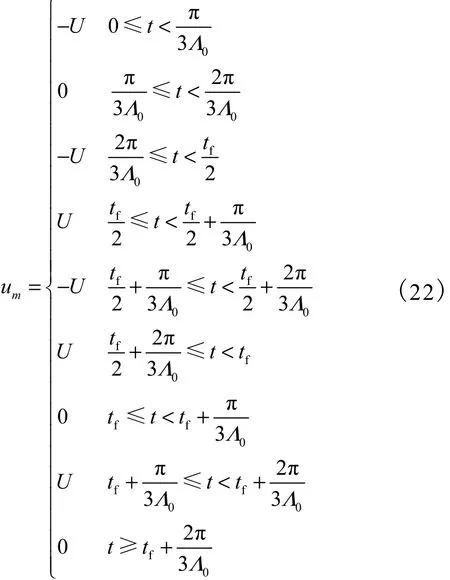
用以上的方法也可以设计多模态情况下的OAT输入整形器,即对每个模态分别设计OAT输入整形器,然后将这些整形器做卷积,得到多模态OAT输入整形器为

值得注意的是:整形输入um作用在系统标称模型上,在有限时间tf+Nπ/Λ0后,um(t)≡0,θm(t )≡0,θ˙m(t)≡0.
4 反馈控制器设计
考虑到以上整形输入mu的脉冲幅值和作用时刻都是由标称模型算出的,且实际系统与标称模型之间存在误差,所以在实际应用中应将输入整形器和其他反馈控制器配合使用,以提高控制性能.本节将利用文献[9]中提出的能量控制方法设计反馈控制器.
由文献[9]知,柔性杆根部的弯曲力矩为
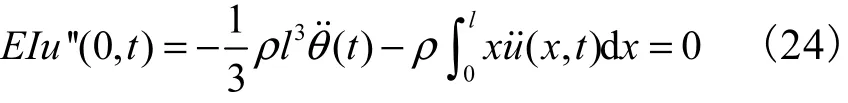
故可将式(5)表示为
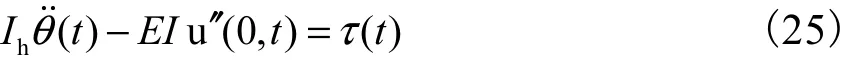
设计轨迹跟踪控制律为

式中pk、vk为正常量;f0k≥.
定理1 由式(25)、式(6)和式(26)构成的闭环系统是稳定的.
证明:选取基于能量的李亚普诺夫函数
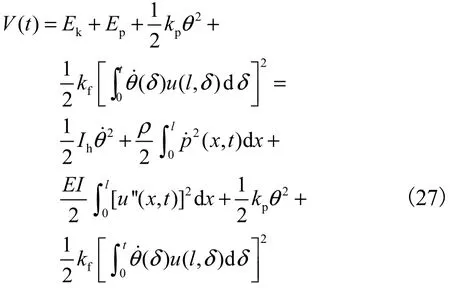
将其沿闭环系统轨迹求导得
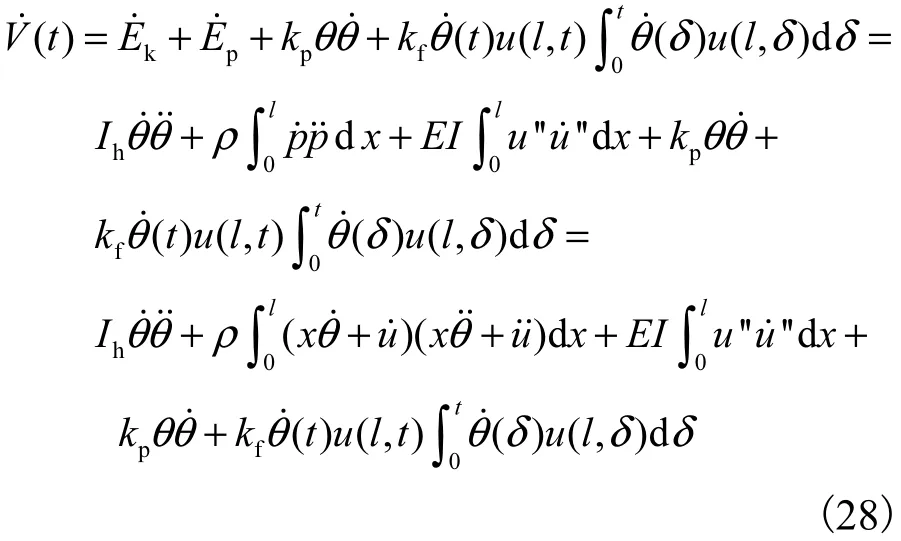
将式(6)代入式(28)可得
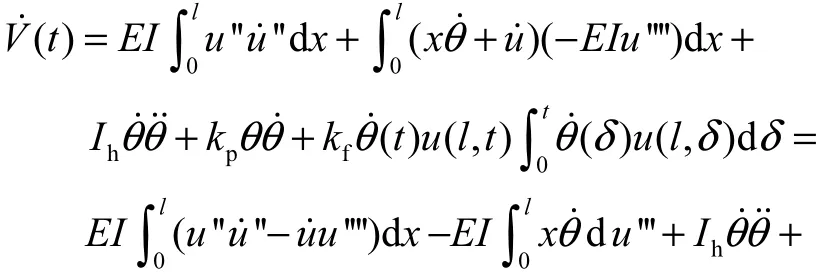
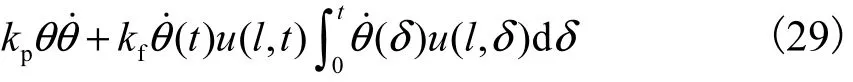
先利用式(7)所示的边值条件来计算式(29)右端的第1项,即
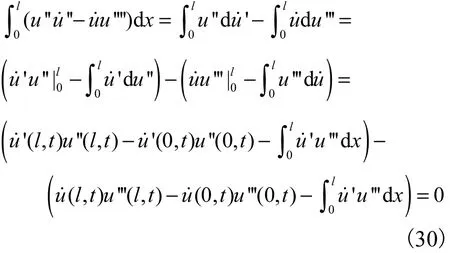
再将式(25)和式(30)代入式(29),并利用边值条件可得

最后将式(26)代入式(31)可得
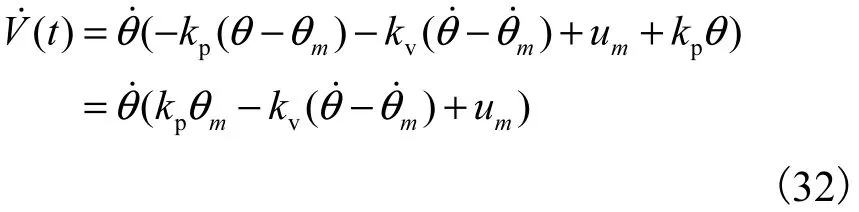
当t<tf+Nπ/Λ0时,um(t)、θm(t )、θ˙m(t)有界,且由于θ˙是连续的,所以在该时间范围内θ(t)和θ˙(t)也均有界,因此V˙(t)是有界的.而当t≥tf+Nπ/Λ0时,因为um(t)≡0,θm(t )≡0,θ˙m(t )≡0,则有

则由李亚普诺夫稳定性理论知:由式(25)、式(6)和式(26)构成的闭环系统是稳定的.
定理2 在控制器式(26)的作用下,柔性航天器转动角度和任意有限的柔性模态渐近稳定.
证明:因当t≥tf+Nπ/Λ0时,um(t)≡0,θm(t )≡0,θ˙m(t)≡0,其后证明与文献[9]相同.
5 仿真研究
为了验证在本文所提出的控制方案,基于柔性航天器标称模型设计具有二阶鲁棒性的3脉冲OAT输入整形器.其中标称模型仅考虑柔性航天器的第1个柔性振动模态,其参数值分别取为:ρm=0.1,kg/m,Jm=0.5,gm=0.06,ωm=15rad/s.进一步可计算得Λ0=14.45,计算时延得Td=0.072,s.
在仿真中实际对象取含4个模态的截断模型为
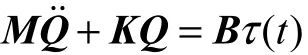
这里Q=[θ,q1,q2,q3,q4]T,而参数
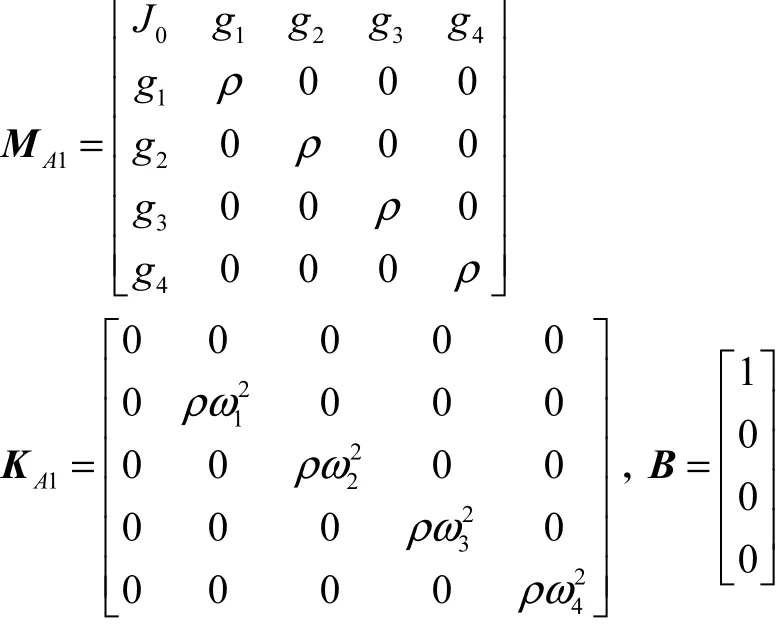
其中各参数分别为:ρ=0.1kg/m ,J0=0.5333,g1= 0.05688,g2=0.00905,g3=0.00359,g4=0.00902,ω1=15.7241rad/s,ω2=98.5412rad/s,ω3=275.9183rad/s, ω4= 540.6898rad/s.
设航天器为完成某项任务需要进行0.5,rad的姿态机动,参考指令中U=1N.柔性杆的振动量用其顶点振动量u(l,t)来描述.能量控制增益分别取为kp=120,kv=16,kf=10000.
首先进行仅使用前馈控制OAT输入整形器时的仿真,图3给出了实际系统第1个模态参数值和标称模型对应参数值之间的误差大于5%时姿态角仿真曲线和参考轨迹的对比.
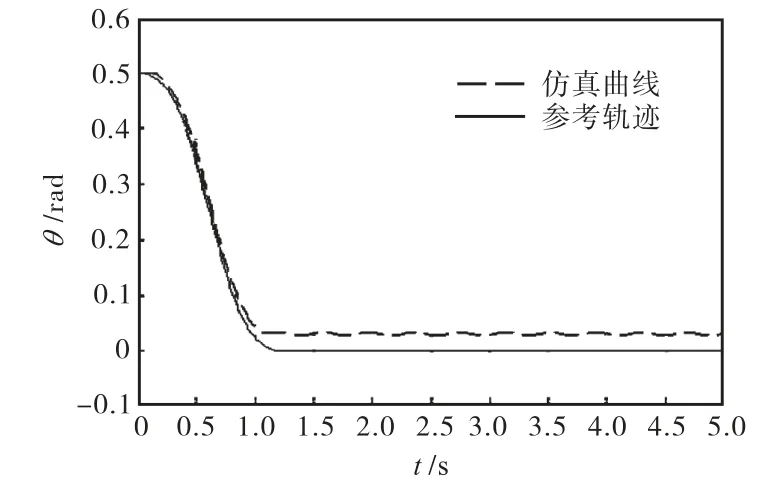
图3 仅使用前馈控制作用时的姿态角仿真曲线Fig.3 Simulation curves of attitude angle only under feedforward control
为比较本文的反馈控制律效果,进行以下两种情况的仿真.
(1)不使用OAT输入整形控制,只使用能量控制的仿真(case 1);
(2)将OAT输入整形与控制能量控制相结合的仿真(case 2).
图4~图6分别为2种控制作用下姿态角跟踪误差、反馈控制量以及振动量仿真结果的比较图.
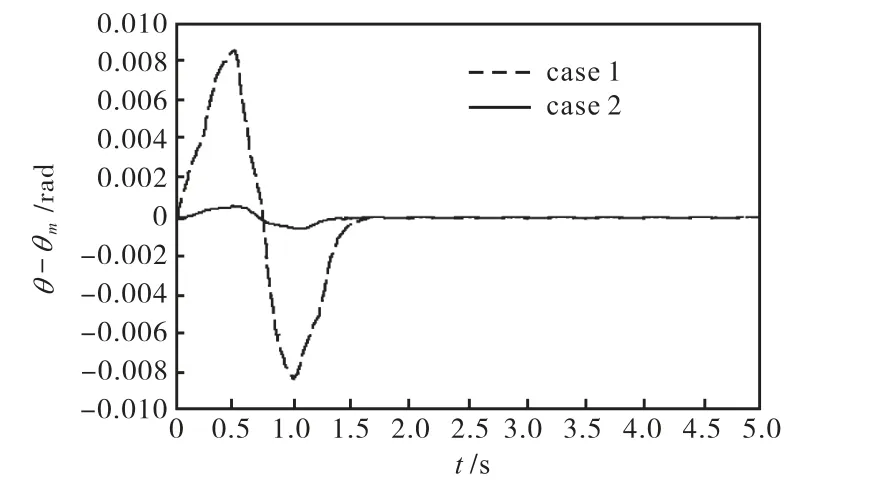
图4 姿态角跟踪误差比较Fig.4 Comparison of attitude angle tracking errors
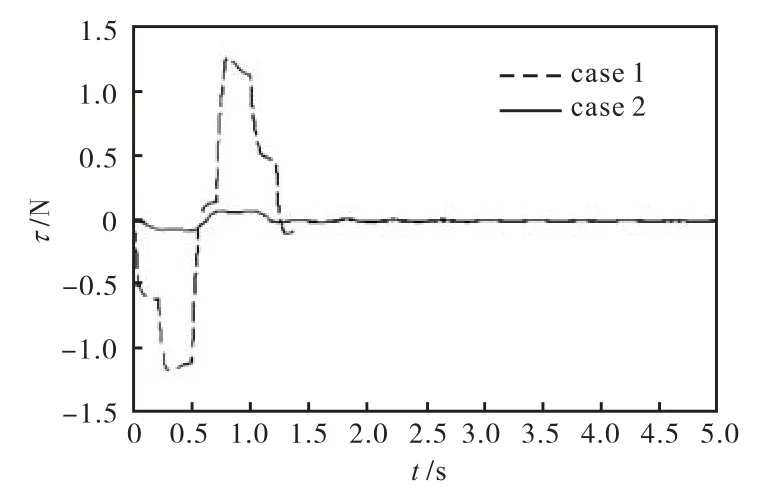
图5 反馈控制量比较Fig.5 Comparison of feedback control
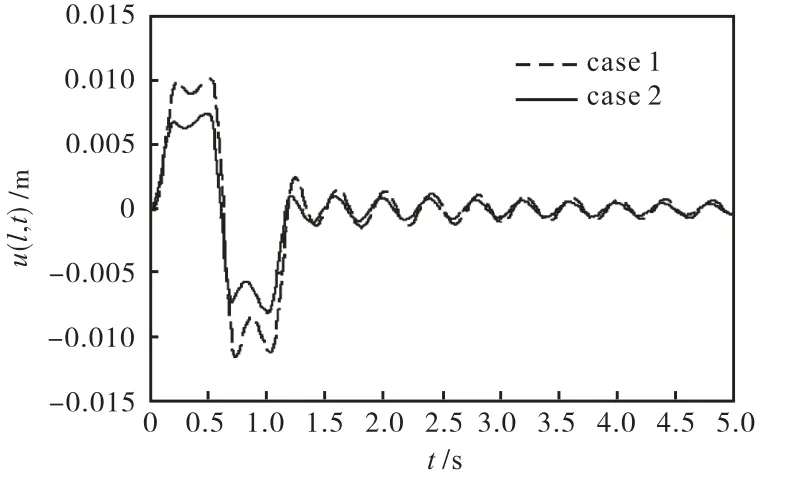
图6 顶点振动量比较Fig.6 Comparison of vibration at end
从以上仿真结果可以得出如下结论:
(1)基于OAT输入整形器的前馈控制在反馈环节不作用时能够保证控制系统的稳定性和基本控制性能,在反馈环节作用时不改变闭环系统的稳定性.
(2)与只使用能量控制比较,将OAT输入整形控制与能量控制结合所得到的状态跟踪效果更好,控制量更小,且跟踪过程中的振动抑制效果也更好.
6 结 语
提出了将基于OAT输入整形器的前馈控制和基于能量关系反馈控制器相结合的柔性航天器姿态跟踪控制设计方法,这一方法不仅保留了能量控制算法简单、不依赖系统模型、可避免模截断误差的优点,且通过引入OAT输入整形前馈控制使得柔性航天器姿态跟踪精度提高,振动量下降,大大减小了控制量;且当反馈环节出现问题时能够保证系统的基本安全和性能.
[1] Feliu V,Rattan K S,Brow H B Jr. Adaptive control of a single-link flexible manipulator[J]. IEEE Control System Magazine,1990,10(2):29-33.
[2] Nathan P J,Singh S N. Variable structure control of a robotic arm with flexible links[C]// Proceedings of IEEE International Conference on Robotics and Automation. Scottsdale,USA,1989:882-889.
[3] Siciliano B,Book W J. A singular perturbation approach to control of lightweight flexible manipulators[J]. Int J Robot Res,1988,7(4):79-90.
[4] Sundareshan M K,Askew C. Neural network-assisted variable structure control scheme for control of a flexible manipulator arm[J]. Automatica,1997,33(9):1699-1710.
[5] Khorrami F,Tzes A. Experimental results on adaptive nonlinear control input preshaping for multi-link flexible manipulators[J]. Automatica,1995,31(1)::83-97.
[6] Smith O J M. Posicast control of damped oscillatory systems[J]. Proceedings of the IRE,1957,45(9):1249-1255.
[7] Singer N C,Seering W P. Preshaping command inputs to reduce system vibrations[J]. ASME Journal of Dynamic Systems,Measurement,and Control,1990,112(1):76-82.
[8] Rhim S,Book W J. Adaptive command shaping using adaptive filter approach in time domain[C]// Proc Amer Contro Conf. San Diego,CA,USA,1999:81-85.
[9] Ge S Z,Lee T H. Non-model-based robust controller design for flexible spacecraft [C]// Proceedings of the 39th IEEE Conference on Decision and Control. Sydney,Australia,2000:3785-3790.
[10] Kanoh H,Tzafestas S,Lee H G,et al. Modelling and control of flexible robots arms[C]// Proc 25th Conf Decision and Control.San Antonlo,Texas,USA,1993:1371-1376.
Attitude Tracking of Uncertain Flexible Spacecraft via OAT Input Shaper and Energy-Based Control
CHEN Yan-hua
(The Seventh Research Division,Beihang University,Beijing 100191,China)
A control approach is presented for attitude tracking and vibration reduction of the uncertain flexible spacecraft by combining the optimal arbitrary time-delay(OAT)input shaping technique and energy-based control scheme. In the proposed approach,the OAT input shaping control,which was designed with nominal model parameters and achieved vibration reduction by shaping the reference command,was implemented as a feedforward control and assured the basic security of the controlled system when the feedback loop was at fault. In order to compensate errors between the nominal model and the real system,a feedback controller was designed with the energy-based control scheme,and the stability of the closed-loop system,involving both feedback control and feedforward control,was verified. Simulation results show that the proposed approach provides better performances.
optimal arbitrary time-delay input shaper;flexible spacecraft;attitude tracking control;energy-based control;vibration reduction
V249.122.2
A
0493-2137(2010)09-0815-06
2009-04-20;
2009-10-14.
国家级实验室和北京市教委共建重点学科资助项目(XK100060422).
陈艳华(1976— ),男,博士.
陈艳华,buaa_sailor@126.com.

