用ANSYS和FLAC3D软件求解边坡稳定安全系数的比较分析

陈 飞,杨诗义,王家成,别小平

(三峡大学三峡库区地质灾害教育部重点实验室,湖北 宜昌 443002)

0 引 言

目前边坡稳定性的分析方法较多,陈祖煜[1]等对此作了较多论述。可以归纳为两类,即定性分析和定量分析方法。定性分析方法主要有工程类比法、图解法等[2]。定量分析方法主要有极限平衡分析方法,例如Sarma法[3]、Bishop法[4]Morgenstern-Price法[5]、Spencer法[6]等,还有建立在塑性力学上、下限定理基础上的极限分析法,以及根据有限元、边界元、离散元等理论编制的软件而进行的数值分析方法。

边坡稳定分析理论具有十分丰富的内容。而基于强度折减的有限元稳定分析方法是目前应用及研究较多的一种分析方法。边坡稳定性分析有限元分析一般采用强度折减法来求得边坡的安全系数。多年来,许多学者致力于这方面的研究,Ugai[7]、Matsui[8]、Griffiths[9]、宋二祥[10]、张鲁渝[11]、赵尚毅[12～14]、郑颖人[12～14]、栾茂田[15]等学者在有限元强度折减法应用方面做了大量的工作。

本文基于强度折减理论,利用有限元软件ANSYS和有限差分软件FLAC3D,联合采用弹塑性数值计算的收敛性和塑性区的贯通性作为边坡的失稳判据,针对算例边坡进行稳定系数求解,进行边坡的稳定性分析。将强度折减理论与FLAC3D软件相结合,并与ANSYS软件分析的结果进行对比分析。

1 有限元强度折减法基本原理及边坡失稳破坏判据

1.1 有限元强度折减法基本原理

1975年,Sienkiewicz[16]等首次在土工弹塑性有限元数值分析中提出了抗剪强度折减系数概念。抗剪强度折减系数定义为:在外荷载保持不变的情况下,边坡内土体所发挥的最大抗剪强度与外荷载在边坡内所产生的实际剪应力之比。外荷载所产生的实际剪应力应与抵御外荷载所发挥的最低抗剪强度即按照实际强度指标折减后所确定的、实际中得以发挥的抗剪强度相等。当假定边坡内所有土体抗剪强度的发挥程度相同时,这种抗剪强度折减系数定义为边坡的整体稳定系数。这里定义的抗剪强度折减系数,与极限平衡分析中所定义的土坡稳定安全系数在本质上是一致的。

国外的Griffiths[9]和Dawson[17]等学者曾利用有限元方法分析土坡和地基的稳定性,确定最危险滑动面,计算表明采用该法所确定的最小安全系数能够保证足够的精度。已有几种分析土工安全系数求解的有限元方法,最主要的是强度折减法。

在边坡稳定分析极限平衡法中,边坡沿着某一滑裂面滑动的安全系数是这样定义的:将土的抗剪强度参数降低为c/Ftrial和tanφ/Ftrial,则土体沿着此滑裂面处达到极限平衡,即将强度参数的储备作为安全系数的定义。而在强度折减法中,安全系数的定义在本质上与传统极限平衡法是一致的。基于强度折减有限元法的边坡稳定分析的基本原理就是将边坡强度参数粘聚力c和内摩擦角的正切值tanφ同时除以一个折减系数Ftrial,得到 c′,并且推导出 φ′。然后作为新的材料参数输入,再进行试算,直至边坡达到极限平衡状态,发生剪切破坏,同时得到临界滑动面,此时对应的折减系数Ftrial即为最小安全系数。折减后的剪切强度参数 c′和φ′为:

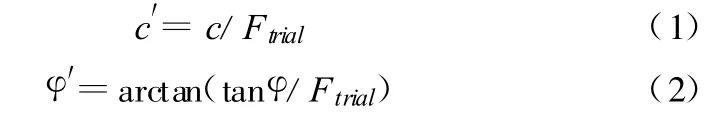
1.2 边坡失稳破坏判据

有限元强度折减法分析边坡稳定性的一个关键问题是如何根据有限元计算结果来判别边坡是否达到极限破坏状态。数值模拟中,对于边坡失稳的判据有很多的观点。连镇营[18]、Matsui[8]以广义剪应变是否贯通作为边坡失稳的评判依据;栾茂田[15]、郑宏[19]、周翠英[20]等以广义塑性应变或者等效塑性应变从坡脚到坡顶贯通作为边坡整体失稳的标志Griffiths[9]、Dawson[17]、郑颖人、赵尚毅[12～14]等以有限元静力平衡计算不收敛作为边坡整体失稳的标志,文献[14]认为塑性区从坡脚到坡顶贯通并不一定意味着破坏,塑性区贯通是破坏的必要条件,但不是充分条件,还要看是否产生很大的且无限发展的塑性变形和位移。综合以上观点并结合FLAC3D程序特点,采用静力平衡计算是否收敛作为边坡是否失稳的评判依据,并结合边坡剪应变增量是否贯通于坡脚至坡顶情况评判边坡整体稳定性。

2 算例分析

2.1 计算模型

均质边坡模型如图1所示。

图1 天然边坡算例

表1为天然边坡模型土工参数取得的初始计算值:

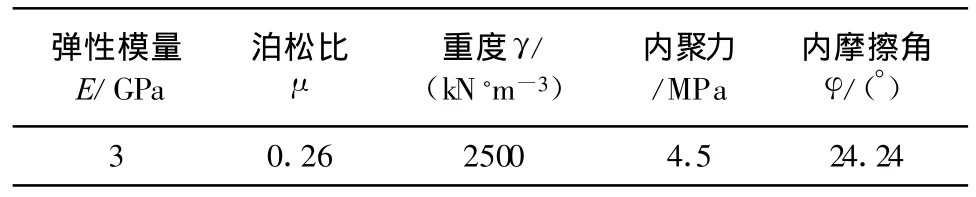
表1 物理力学参数初始计算取值

2.2 采用ANSYS进行边坡模型稳定性计算分析

利用强度折减有限元法对该边坡进行了稳定性分析。采用ANSYS中D-P理想弹塑性材料模型,前后处理均在ANSYS中进行。边界条件设为左右两侧水平约束,底边为竖向约束,坡面为自由边界。其模型网格图如图2所示。

图2 划分好的网格

在重力荷载作用下,算例边坡在强度折减系数分别取为1.05,1.10,1.15,1.20,1.25,1.30,1.35的情况下,边坡内塑性应变是在不断发展变化的。

现选取强度折减系数分别为F=1.30和F=1.35,对这两种情况下的等效塑性应变的变化情况进行分析和总结,结果如图3、图4所示。

图3 F=1.30塑性应变云图

当F=1.30时,有限元静力平衡计算收敛,塑性区没有完全贯通。

图4 F=1.35塑性应变云图

当F=1.35时,有限元静力平衡计算不收敛,塑性区完全贯通。

从边坡模型的塑性区云图看,随着强度折减系数F的增加,塑性区逐渐增大,当 F=1.35时,塑性区贯通至坡顶,并且此时解不收敛,表明此时边坡已经破坏。根据边坡失稳破坏判据可以判断出边坡的稳定安全系数为1.35。

2.3 采用FLAC3D进行边坡模型稳定性计算分析

FLAC3D在计算岩土工程上功能强大,但利用它建立模型难度大,费时费力且容易出错,而有限元软件ANSYS在前处理方面则有着相当的优势,文章巧妙的运用了ANSYS TO FLAC3D接口程序,以此取长补短,克服了FLAC3D本身在前处理方面的不足,取得了令人满意的效果。本文采用ANSYS建立模型、分配材料属性、划分网格,然后采用 ANSYSTOFLA C3D接口程序把模型导入 FLAC3D。FLAC3D和ANSYS所采用的单元体形状大都相同,但其每一单元节点编制的规则和节点坐标,以及单元的材料属性,即单元数据,却有一定的差别。因此,根据这2种软件单元形状及其单元数据的关系,作者采用Visual C++语言编制了ANSYSTOFLAC3D接口程序软件,为本文成功实现模型导入提供了帮助。程序的界面如图5,此程序需要ANSYS输出的节点文件和单元文件,然后转化成FLAC3D识别的格式。

图5 程序界面图

图6 未达到移动时的位移云图

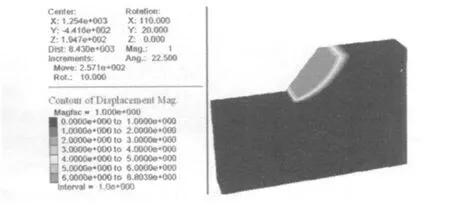
图7 塑性区贯通时的位移云图

如图6所示,折减系数为 1.348,算法收敛,塑性区没有贯通。

当折减系数为1.349时,算法收敛,土坡产生较大位移,同时塑性区贯通坡脚至坡顶.可判断此折减系数下,边坡稳定性急剧下降,产生滑动。根据边坡失稳破坏判据确定土坡稳定系数Fs为1.349。

图7可以看出塑性区的分布情况,这有助于了解边坡整体失稳破坏的发生、发展过程,掌握边坡失稳机制,为进一步研究边坡开挖、支护时稳定问题提供了较为直观的依据。

3 结 论

(1)采用强度折减系数法,利用FLAC3D软件对边坡的稳定性进行分析,可求得边坡稳定系数,与采用ANSYS软件计算结果相比较,结果是相近的。表明强度折减系数法利用FLAC3D软件在分析边坡的稳定性方向上是合理、可行的。利用FLAC3D软件进行边坡的安全系数分析具有可行性。

(2)分析中采用算法的收敛性、剪应力增量贯通坡脚至坡顶作为边坡破坏的标准是适应的。

(3)采用连续介质快速拉格朗日分析法的优点不仅仅在于求得稳定系数,对于复杂地貌、地质的边坡可自动求出任意形状的临界滑裂面,并能模拟出边坡开挖、支护、失稳过程,且可采用不同的本构关系,考虑岩土体的非线性,克服了极限平衡分析方法的不足,对工程实践有很好的指导意义。

[1]陈祖煜,汪小刚,杨建,等.岩质边坡稳定分析—原理·方法·程序[M].北京:中国水利水电出版社,2005.

[2]黄昌乾,丁恩保.边坡工程常用稳定性分析方法[J].水电站设计,1999,15(1):53-58.

[3]Sarma S K.Stability analysis of embankments and slopes[J].Journal of Geotechnical Engineering Division,ASCE,1979,105(12):1511-1524.

[4]Bishop A W.The use of the slip circle in the stability analysis of slope[J].Geotechnique,1955,5(1):7-17.

[5]Morgenstern N R,Price V E.The analysis of stability of general slip surfaces[J].Geotechnique,1965,15(1):79-93.

[6]Spencer E A.Method of analysis of the stability of embankments assuming parallel interslice forces[J].Geotechnique,1967,17(1):11-26.

[7]Ugai K.A method of calculation of total factor of safety of slopes by elaso-plastic FEM[J].Soils and Foundations,1989,29(2):190-195.

[8]Matsui T,San K C.Finite Element Slope Stability Analysis by Shear Strength Reeducation Technique[J].Soils and Foundations,JSSMFE,1992,32(1):59-70.

[9]Griffiths D V,Lane P A.Slope stability analysis by finite elements[J].Geotechnique,1999,49(3):387-403.

[10]宋二详.土工结构安全系数的有限元计算[J].岩土工程学报,1997,19(2):1-7.

[11]张鲁渝,郑颖人,赵尚毅,等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报,2003,34(1):21-27.

[12]赵尚毅,郑颖人,时卫民,等.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报,2002,24(3):343-346.

[13]赵尚毅,郑颖人,邓卫东.用有限元强度折减法进行节理岩质边坡稳定性分析[J].岩土力学与工程学报,2003,22(2):254-260.

[14]赵尚毅,郑颖人,张玉芬.极限分析有限元法讲座-Ⅱ有限元强度折减法中边坡失稳的判据探讨[J].岩土力学,2005,26(2):332-336.

[15]栾茂田,武亚军,年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报,2003,23(3):1-8.

[16]Sienkiewicz O C,Humpeson C,Lewis R W.Associated and nonassociated visco-plasticity in soil mechanics[J].Geotechnique,1975,25(4):671-689.

[17]Dawson E M,Roth W H,Drescher A.Slope stability analysis by strength reduction[J].Geotechnique,1999,49(6):835-840.

[18]连镇营,韩国城,孔宪京.强度折减有限元法研究开挖边坡的稳定性[J].岩土工程学报,2001,23(4):406-411.

[19]郑 宏,李春光,李焯芬,等.求解安全系数的有限元法[J].岩土工程学报,2002,24(5):323-328.

[20]周翠英,刘祚秋,董立国,等.边坡变形破坏过程的大变形有限元分析[J].岩土力学,2003,24(4):644-652.