基于特征参数归一化的鲁棒语音识别方法综述

肖云鹏, 叶卫平

(北京师范大学 信息科学与技术学院，北京 100875)

1 引言

目前，语音识别技术已经取得了很大的成就,然而绝大多数识别系统仍然局限于在安静的环境下使用。在实际环境中，往往会因为环境中复杂因素的影响，造成训练环境和测试环境存在不匹配现象，使得识别系统性能大幅度下降，极大地限制了语音识别技术的应用范围。正因如此，鲁棒语音识别技术长久以来一直被视为重要的研究领域，并取得了初步性地进展。其主要是对语音信号本身、语音特征参数或模型参数做适当的处理与调整，以减少噪声干扰的影响，降低训练环境与测试环境不匹配的情形或提升语音信号特征参数本身的鲁棒性，进而提高系统的性能。

根据噪声对语音频谱的干扰方式不同可以把噪声分为加性噪声和乘性噪声两类：

(一) 加性噪声(Additive Noise)

加性噪声为录制语音时，原始语音与背景噪声以线性相加的方式同时被收录进去，即所采集到的语音信号为纯净的语音信号和噪声的和。这种噪声在日常生活中很容易接触到，例如实际环境中的风声雨声、办公室里的打印机的工作声、计算机中的磁盘驱动器和风扇等设备的声音以及周围说话人的声音等等。

(二) 卷积性噪声(Convolution Noise)

卷极性噪声通常是指语音信号在由不同通道传输时所产生的通道效应(Channel Effect)，例如电话线路效应、麦克风通道效应等等。其与语音在频谱是相乘的关系，在时域上是卷积关系，故称卷积性噪声。加性噪声和卷极性噪声对语音信号的干扰过程示意图如图1所示。

图1 噪声干扰示意图

近年来，越来越多的学者致力于鲁棒语音识别的研究，许多鲁棒语音识别技术成功地被提出，这些技术的目标都是相同的，主要是提高语音的鲁棒性，进而提高识别率，使语音识别技术能够更广泛地应用到日常生活中的各个方面。依据方法本质的不同大体可分为三类解决方法[1]：

(一) 语音增强技术(Speech Enhancement Techniques)

置于识别器前端，消除测试语音中噪声的影响，提高语音信号本身的质量。所有操作基本都是针对原始语音波形而进行的，与后续的特征提取及模型匹配没有直接关系。通常假设语音信号与噪声信号二者在统计上是不相关的，力求能由带噪语音信号中重建出干净语音信号。常见的技术有谱减法(Spectral Substraction)[2]、卡尔曼滤波器(Kalman Filter)[3]、信号子空间方法(Signal Subspace Approach)[4-5]等。

(二) 鲁棒性语音特征(Robust Speech Feature)

寻找稳健的耐噪声的语音特征参数和对从含噪语音中提取的特征进行处理。其处理的基本思想就是去除由噪声引起的带噪语音特征与纯净语音特征之间的偏差，主要通过对语音特征的一些统计特性(如均值、方差)或分布归一化来实现。常见的技术有倒频谱均值消去法(Cepstral Mean Subtraction, CMS)[6]、倒频谱归一化法(Cepstral Normalization，CN)[7]以及直方图均衡化(Histogram Equalization，

HEQ)[8-9]等等。

(三) 声学模型自适应技术(Acoustic Model Adaption Techniques)

由少量的自适应语料调整由干净语音或不同环境下语料训练而成的声学模型中的概率分布参数，如均值向量和混合高斯模型的协方差矩阵，希望调整后的模型可以适用于测试语料的环境，以降低环境不匹配的影响。在实际应用中，由于它直接调整语音模型参数来降低环境噪声产生的不确定度，常常产生较好的效果。常见的技术有最大后验概率法(Maximum a Posterior，MAP)[10]，最大相似度线性回归法(Maximum likelihood Liner Regression，MLLR)[11]等。

上述三类方法中，第一类和第二类方法属于语音识别系统前端处理环节。其中，大多数语音增强算法是以提高输入信号的信噪比为目的，使受到噪声干扰的语音听起来会比较接近无噪环境下的语音，往往在提高语音识别系统的识别率上效果并不显著。第三类方法属于后端处理环节，目的是让识别器中的隐马尔科夫模型(Hidden Markov Model，HMM)更适用于实际环境。这类方法的优点是需要少量的自适应语料就能对声学模型进行调试；缺点就是在进行自适应调试时，计算量很大。本文将讨论的基于特征参数归一化的鲁棒语音识别方法属于第二类鲁棒性语音特征，其简单和实用性，是声学模型自适应技术和大部分语音增强技术无法比拟的，所以常常被作为鲁棒语音识别的首选方法[12]。

2 语音归一化的依据

2.1 噪声对语音统计特性的影响

语音的统计特性(如均值，方差)能提供许多由噪声引起的语音倒频谱偏差的相关信息。理论上讲，在数学研究中，只有前四阶矩(Moment)具有明确的物理含义，分别为均值、方差、偏度(Skewness)和陡峭度(Kurtosis)。

均值μ定义如下：

(1)

其中，X(n)是倒频谱系数序列，T是特征序列的长度。

方差是二阶中心矩：

σ=E[(X-E[X])2]=E[X2]-E[X]2

(2)

高阶矩可通过分布的均值来得到。N阶中心距(Central Moments)定义如下：

MN=E[(x-μ)N]

(3)

偏度和陡峭度分别为三阶中心矩M3和四阶中心矩M4，它们分别描述了倒频谱分布的对称性和相对平坦度。

加性噪声对语音统计特性的影响并非是纯净语音和噪声语音统计量的简单相加或变换， 但统计特性在一定程度上也能反映噪声对倒频谱分布的影响趋势。

图2为在几种不同信噪比的背景噪声污染下的第一维倒频谱分布。统计语料内容来自16名男女录制的1 232句话。可以看上，倒频谱特征的全局的均值和方差均有所偏移。其中，均值随着信噪比的降低而提高，而方差随着分布的坡度(Slope)的增加而降低。此外，偏度也有所移动，在高信噪比表现出来的双峰(Bimodal)特性随着信噪比的降低逐渐显示出单峰特性。

图2 加入不同信噪比的噪声后第一维倒频谱的分布

图3为纯净语音、噪声和带噪语音(信噪比为10dB)的倒频谱的前四个统计特性。第一行描述了除了0阶倒频谱以外的12阶倒频谱系数的均值；下面三行描述了全部13阶倒频谱系数的方差、偏度及陡峭度。可以看出，在加性噪声的影响下，语音信号倒频谱的方差和其他统计属性均有所降低，这就导致了识别过程中的环境不匹配，从而造成识别率低下。可以假设，如果对倒频谱的这些特性进行归一化，那么环境不匹配程度就可以被降低或补偿。

图3 纯净语音、噪声和带噪语音的MFCC_0的统计属性

2.2 标准的用于鲁棒语音识别的语料库AURORA

为了评价在噪声环境下各种鲁棒语音识别算法的性能，需要建立一个标准的带噪语音数据库。一是可以比较各种鲁棒语音识别算法的相对有效性；二是可以验证算法的合理性以及允许他人有条件评估你的算法。AURORA语料库就是为此目的而发行的语料库，其中最常用语料库的是AURORA 2.0和3.0。AURORA 2.0是在TI-DIGIT语料库基础上，内容为美国成年男女录制的一系列连续的英文数字串，人工加上不同加性噪声和通道噪声的干扰。AURORA 3.0是欧洲语言车载语音数据库(SpeechDataCar)的一个子集，是在实际车载环境下录制的数字串语音数据文件，包含四种欧洲语言。此外，AURORA 工作组成员还为噪声环境下语音识别系统的评估的实验框架提供了标准设置，包括前端预处理、特征提取、训练和识别过程涉及到的主要参数都提供了参考数据，并在此基础上给出了未使用任何鲁棒技术的参考性的识别结果，这为各种鲁棒语音识别算法的评估和比较提供了必要条件[14]。本文所提到的算法都在AURORA数据库上验证了有效性。

3 归一化方法介绍

语音特征的统计特性受噪声环境的影响，归一化方法应用于语音识别系统当中来补偿环境噪声不匹配的影响，进而来提高系统的识别率。大多数归一化方法都应用在倒频谱域，作为语音特征的后加工。其中，梅尔倒谱系数(Mel-Frequency Cepstral Coefficients)为大家接受并认同的一种特征，各种各样的鲁棒语音技术都是基于这种特征发展而来的。它的优点是不需要任何噪声环境的先验知识和自适应方法，实现方法简单，而且效果比较理想。本节对各种归一化算法进行介绍。

3.1 倒频谱矩归一化(Cepstral Moment Normalization)

倒谱均值归一化法(Cepstral Mean Normalization，CMN)[15]，倒谱方差归一化(Cepstral Variance Normalization，CVN)[16]以及高阶倒谱矩归一化(Higher Order Cepstral Moment Normalization，HOCMN)[13,17]都属于对倒谱矩的归正方法，目的是使带噪语音特征参数的概率密度函数(Probability Density Function，PDF)更接近纯净语音的概率密度函数，以减少测试语料和训练语料环境的不匹配度。其中，CMN是对一阶矩做归一化，CVN是对CMN的补充，在CMN的基础上再对二阶矩进行归一化。这两种方法都是常用的方法，CMN在倒谱域去中除了直流分量，这些直流分量包含了大部分信道失真，而CVN对方差的进一步归一化进一步减少了带噪语音信号和纯净语音信号的概率密度函数的差异。而HOCMN是对高阶矩(大于3)进行归一化，取得了更好的效果。下面采取统一的公式对上述方法进行描述[15-17]。

倒谱序列X(n)的N阶矩定义如下：

(4)

其中，X(n)是倒频谱系数序列，T是特征序列的长度，该序列的N阶距就是对XN(n)取期望值。

语音信号的倒谱系数的概率密度函数通常被看作准高斯分布(Quasi-Gaussian Distribution)。在这个前提下，其倒谱特征的奇次阶距(Odd Order Moments)应为0，偶次阶距(Even Order Moments)应为某一特定的常数[17]。N阶距归一化的目的是：

(5)

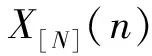
有了上述的表示式，可以将上文提到的CMN和CVN的定义如下：

(6)

(7)

其中，X[L,N]是X(n)的L和N阶距同时被归一化后对应的序列。所以，CVN总是和CMN结合一起使用，所以也称为均值方差归一化(Mean and Variance Normalization，MVN)。

偶次N的HOCMN总是和一阶矩归一化同时存在的，并满足如下关系式：

X[1,N](n)≜bX[1](n)=bXCMS(n)

(8)

其中，b为比例因子。

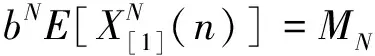
(9)

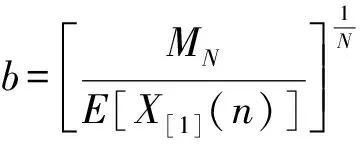
如果N的值比较大，b可以通过下式来近似

(10)

可以看出，只要给定不同的N就可以对序列X(n) 的第N阶矩进行归一化，换句话说，对于不同的N，我们就能得到不同的比例因子b。

奇次的HOCMN是由三阶矩倒谱矩归一化[18]扩展而来的，它也是在一阶矩归一化的基础上进行高阶归正的。其满足下式：

(11)

上式中，

(12)

(13)

上式展开后，当a很小时，我们可以把高次项去掉，仅保留最后两项，这样a就可以近似表示成为：

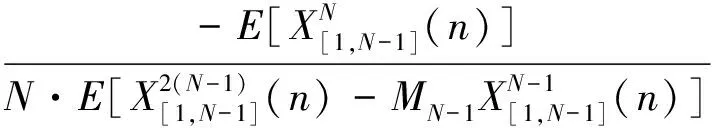
(14)

由于公式仅是一个近似计算，存在一定误差，递归算法如图4所示能得到更精确的结果。

图4 奇次阶HOCMN的流程

可以看出，在对高阶矩进行归一化前均会先进行CMN，也就是说，经过HOCMN作用后的特征参数各维的均为都为0。对于奇次阶距和偶次阶距都进行归一化的HOMVN可以通过一个串联系统来实现，先对特征系数进行奇次阶距的归正，再进行偶次阶距的归正，如图5所示。

图5 奇次阶和偶次阶HOCMN的级联系统

C.W.Hsu and L.S.Lee提出使用HOCMN能消除测试语料和训练语料之间残余的不匹配，效果优于CMN和CVN，并指出最优的倒谱矩组合模式为HOCMN[1,5,100][17]。但也可以看出，随着L和N的增长，算法复杂度越高，收敛速度越来越慢。

3.2 直方图均衡化法(Histogram Equalization，HEQ)

CMN和CVN在一定程度上补偿了信道失真和加性噪声产生的负面影响，但是他们线性的本质使其不能很好地解决各种环境噪声产生的非线性失真。解决办法除了上面所述的对高阶矩进行进一步归一化以外，直方图均衡化[8,19]也是一种有效的方法。

直方图均衡化作为一种特征补偿技术起初是在数字图像处理中被提出的[8]， 是一种采用压缩原始图像中像素数较少的部分, 拉伸像素数较多的部分, 从而使整个图像的对比度增强、图像变清晰的方法，在图像处理领域得以广泛的应用。近几年来不少学者将其成功地应用到语音处理上[20-24]。比如, Torre[8]等将其应用到语音识别上以提高系统鲁棒性。实际上, 直方图均衡化就是一个样本的非线性变换, 目的是使得变换后的样本服从我们所需要的参考分布。直方图均衡化方法是一种非线性的补偿变换, 其不仅仅对特征分布的一阶和二阶矩进行归一化, 而是试图匹配训练和测试语料特征参数的分布，即对概率分布的所有阶矩都进行所有归一化, 使得训练和测试的语音特征之间的不匹配程度降低, 从而提高系统的识别性能。

3.2.1 直方图均衡化的基本原理

HEQ的假设前提是训练语料的语音特征参数的统计分布和训练语料特征参数的统计分布(也可称为参考分布)是一致的。由于语音特征矢量是多维的，为了简化模型, 通常假定特征矢量各维分量相互独立, 由此我们可以在特征的每一维分量上独立进行直方图的非线性变换。假设x为测试语句语音特征向量的某一维特征参数，其概率密度函数(Probability Density Function)为PTest(x)，参考概率密度函数为PTrain(x)，变换后的矢量为y，其服从参考概率密度函数PTrain(x)，变换记为F(x)。直方图变换可以看成将原变量的直方图变换到参考的直方图，以达到将原变量变换到目标变量的过程。

HEQ原理图见图6。

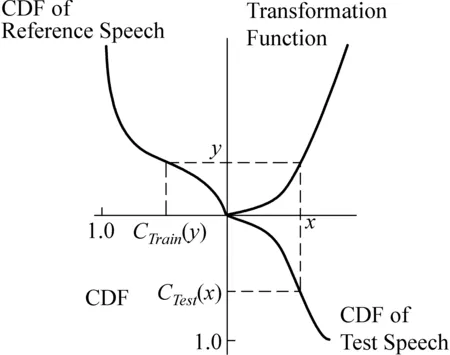
图6 HEQ的基本原理

根据直方图的定义，经变换后的小面积元对应相等，即

Ptrain(y)dy=PTest(x)dx

(15)

设F-1(y)为F(x)的反函数，若上述关系式以累积概率密度函数(Cumulative Probability Function)表示出来，可得到测试语句累积密度函数CTest(x)和训练语料密度函数CTrain(y)之间的关系为：

(16)

=CTrain(y)

从上式可得到将原样本空间变换到参考分布空间的变换函数为：

(17)

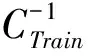
值得注意的是，在实际应用中语音特征参数为一有限集合，所以无法非常准确估算实际的累积分布函数，通常使用累积直方图(Cumulative Histogram)去近似累积分布函数。

3.2.2 查表式直方图均衡化法(Table-Based Histogram Equalization，THEQ)

THEQ[19]是一种直方图均衡化的一种具体实现方法。其对于所有训练语料而言，将语音特征向量的每一维分量统计出一个累积直方图。然后以表格方式将累积直方图所有信息进行存储，用来当做转换的参考分布。对于测试语料语音特征向量的每一维也采用同样的方法统计出累积直方图，在进行均衡化的过程中，进行查表(Table-Lookup)转换，每个区间内特征值用先前建立好参考分布的特征值逐一取代。

不难看出，THEQ需要将庞大的表格信息加载到内存中才能进行转换匹配动作，而且若要有良好的补偿效果，表格所记录的点数不能太少，但当表格记录点数增加时，需耗费更大量的内存空间与进行查表转换的处理器运算时间。

3.2.3 分位数直方图均衡化法(Quantile-based Histogram Equalization，QHEQ)

QHEQ是一种参数型的直方图均衡化方法[25-26]，其对于语音特征向量的每一维利用转换函数H(x)进行均衡化，欲使转换后的语音特征参数的统计分布能够和参考分布相似。数学关系式表示如下：

(18)

其中，x为待转换的特征参数；QK为整个语句中该维特征参数中的最大值；α和γ为转换因子，可通过下式求得：

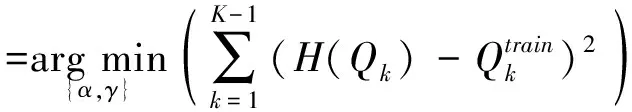
(19)

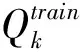
就是说在对于每一句话进行均衡化前，需要进行分位数校正，以求得最佳的参数α和γ，此校正是以最小均方误差为准则进行的。

QHEQ虽然转换过程不像THEQ需通过大量的查表动作, 只需使用少量的参数即可进行等化动作, 但是对每一句待转换的语句在进行转换动作前, 必须利用格式搜寻以在线实时运算求取参数, 因此所需的处理器运算时间也是相当可观的。

传统的两种直方图均衡化方法虽然能有效补偿噪声产生的非线性失真，但无论是传统的查表直方图均衡化法还是分位数直方图均衡化法，在实现的过程中，需要耗费大量的存储空间或是处理器运算时间。为了解决这个问题，Shih-Hsiang Lin等[9]提出了用数据拟合的概念求累积分布函数的反函数，只需使用少量的多项式系数与多项式函数，便能迅速地将测试语料语音特征向量每一维德统计分布转换至先前已从训练语句中定义好的参考分布，不能拥有和直方图均衡化相同的效果。

3.3 倒频谱形状归一化法(Cesptral Shape Normalization)

前面介绍的归一化方法使识别系统在各种噪声环境下性能有所提升，但都存在各自的缺陷。比如直方图均衡化HEQ需要大量的训练语料才能估计出比较精确的特征分布，而高阶倒频谱矩归一化HOCMN的奇次阶距很难准确地估算出来。中国科技大学王仁华等提出了倒频谱形状归一化法(Cesptral Shape Normalization，CSN)[28]，其在一定程度上解决了这两种方法存在的问题，同时能达到很好的鲁棒效果。它仅需要估算出一个适当的形状因子(Shape Factor)，而形状因子能简单而准确地估算出来。此外，与传统的归一化方法相比，CSN有更明确的物理意义和更强的正对性。

CSN使用广义高斯密度函数(Generalized Gaussian Density，GGD)[29-30]来描述噪声环境下每一维语音特征分布，GGD的概率密度函数PDF定义如下：

(20)

其中

(21)

这里，Γ(·)为Gamma函数。

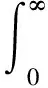
(22)

其中，参数v描述了指数衰减率。

CSN算法描述如下：

步骤1：首先

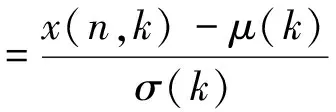
(23)

这里，x(n,k)为第n帧的第k维特征；μ(k)和σ(k)为当前语料第k维特征序列的均值和方差。

步骤2：利用指数因子来实现倒频谱形状归一化:

z(n,k)=[y(n,k)]α(k)

(24)

其中，α(k) 表示第k维特征对应的形状因子(Shape Factor)。上述公式的目的就是使处理过的特征满足参考分布(Reference Distribution)。CSN采用了矩匹配估计(Moment Matching Estimator)方法[29]。

广义高斯分布的r阶中心距(Central Moment)定义如下：

(25)

其中，E[·]表示取均值操作。将公式(20)带入公式(25)可得到:

(26)

广义高斯比例函数(the Generalized Gaussian ratio Function)如下：

(27)

基于上述公式，定义如下方程：

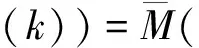
=0

(28)

α(k),

(29)

其中，N为帧数。

显然，α(k)是方程(25)的根。尽管方程没有闭合解，但F(α(k))是α(k)的递增函数，可通过割线法求得。这里，有两个参数需要设置：形状参数v0和矩的阶数r。实验表明：v0=2和r=2就能得到比较好的实验结果。

此外，文献[28]给出了以上三种方法在Aurora2.0和3.0的识别率比较。其中，CSN的平均识别高于HEQ，HEQ高于HCOMN和CMVN。下面给出在纯净语料训练模型的各种归一化方法的在语料库Aurora2.0识别率比较，具体参数设置和其他识别结果参照文献[28]。

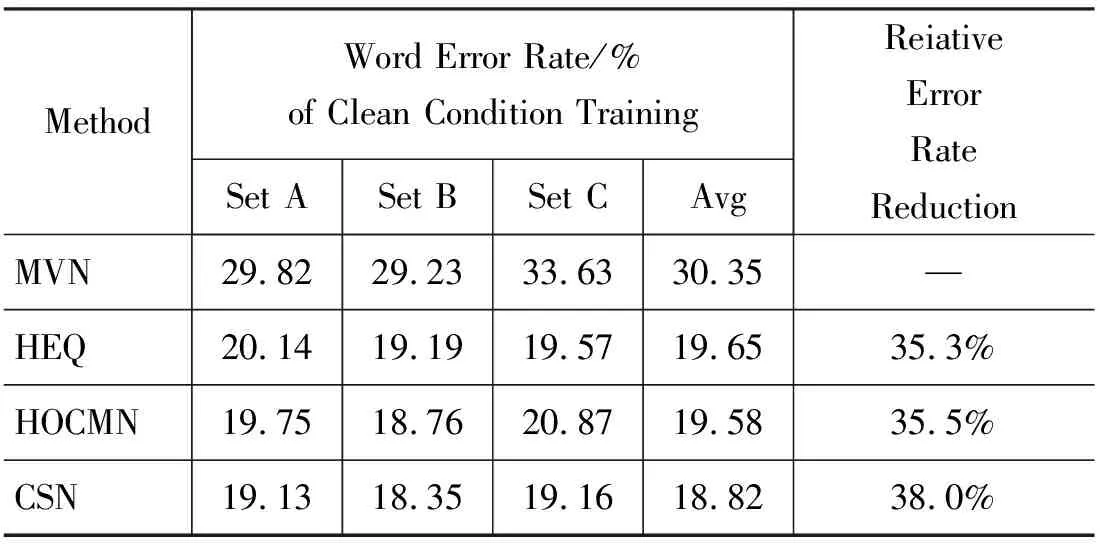
表1 CSN和其他归一化方法在不同测试集下的识别率比较

对特征参数概率分布的实验表明，在有噪声影响的情况下，特征参数通常呈现双峰分布，鉴于此，中国科技大学王仁华等提出了一种新的基于双高斯混合模型(Gaussian Mixture Model，GMM)的特征参数归一化方法[31]，以提高语音识别系统的鲁棒性。该方法采用更为细致的双高斯模型来表达特征参数的累积分布函数(CDF)，并依据估计得到的CDF进行参数变换将训练和识别时的特征参数的分布都归正为标准高斯分布，从而提高识别率。在Aurora 2和Aurora 3数据库上的实验结果表明，基于双高斯的归一化方法的性能明显好于传统的倒谱均值归一化(CMN)和倒谱均值方差归一化方法(CMVN)，而与非参数化方法—直方图均衡化的性能相当。

3.4 调频谱归一化法(Modulation Spectrum Normalization)

上述介绍的方法是对语音特征的概率分布及统计特性进行归一化，除此以外，还可以修正语音特征的功率频谱密度(Power Spectral Density，PSD)函数[33-34]，将其归一化至一参考的PSD，以得到新的语音特征参数，来降低噪声对语音的影响。

调频谱(Modulation Spectrum)的概念首先是由Houtgast 和 Steeneken提出的[32],语音信号的调频的含义和通信系统中的幅度调制类似。由于语音信号是宽带信号，往往对其频谱划分为若干个频带再进行后续处理。每个频带内信号的能量包络称为该带宽的调制信号，这个调制信号的功率频谱密度函数(PSD)就是调频谱。需要强调的是，调频谱不仅适用于原始语音信号，同样适用于倒频谱系数。

3.5 时间序列结构归一化法(Temporal Structure Normalization，TSN)

新加坡大学李海洲等，提出了一套时间序列滤波器设计的新方法，称为时间序列结构归一化法[33]，是调频谱正规化法的一种典型的实现方法。其此目的在于将语音特征序列的功率谱密度归一化，使其轮廓逼近于一参考功率频谱密度。基于AURORA-2数据库，实验结果表明：当此方法所得的时间序列滤波器作用于CMVN与MVA处理后的梅尔倒谱特征参数时，在各种噪声环境下所得的语音识别率都有大幅度改进。

TSN具体实现方法如下，可参见图7：

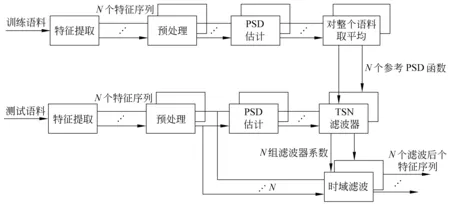
图7 TSN原理图

(1) 估计每一句训练语料和测试语料的第j维特征序列的功率频谱密度(PSD)，分别记作Ptest(k,j)和Ptrain(k,j)。然后，将训练语料所有句子同一维的PDS作平均，所得即为参考PDS。

Pref(k,j)=E{Ptrain(k,j)}

(30)

(2) TNS使用滤波器的幅度响应定义如下：

(31)

(3) 进一步求取该滤波器的脉冲响应(Impulse Response)，即对上式的|H(k,j)|进行逆离散傅立叶变换(IDFT)：

h(τ,j)=IDFT(|H(k,j)|)

(32)

(4) 对上述滤波器系数乘以汉宁窗(Hanning Window)以较少截断效应：

(τ,j)=h(τ,j)·w(τ)

(33)

其中：

(34)

0≤m≤M-1

(5) 将滤波器系数总和归一化为1，以达到直流增益归一化的目的：

τ,

(35)

TSN法对语音特征具有较好的鲁棒化效果，且执行复杂度极低，但仍有待改进之处，首先TSN所得的初始滤波器系数是参考频率响应的逆函数求得，然后将这些系数乘上一个汉宁窗以减缓不当高频成分产生，此求取滤波器的方法未必是最佳化的，所得滤波器系数的频率响应与参考频率响应之间误差较大；其次，在TSN法中，滤波器系数和被归一化为1，代表直流增益为一定值，此步骤使归一化的特征参数的功率频谱密度并不一定接近参考功率频谱密度，只是轮廓上大致相同；最后，TSN是在MVA处理后的基础上再对梅尔倒谱系数进行处理，进而得到良好的效果，但单独使用改进效果并不明显。

鉴于TSN存在的一些问题，国立暨南国际大学电机工程学系王致程等进而探讨发展出了更精确更有效的调频谱归一化技术，提出了三种新方法分别为等波纹时间序列滤波器设计法(Equi-Ripple Temporal Filtering，ERTF)、最小平方频谱拟合法(Least-Squares Spectrum Fitting，LSSF)以及幅度频谱内插法(Magnitude Spectrum Interpolation，MSI)[35]，实验结果表明ERTF、LSSF以及MSI法与传统的TSN相比在各种不同的噪声环境下识别率均有明显提升，且并不需要与MVN或MVA法结合，也能有效处理梅尔倒谱特征因噪声干扰所造成的失真。然而当它们与MVN或MVA法结合时，也可以得到更加的识别准确度。

4 总结

本文介绍了目前基于语音特征归一化来实现鲁棒语音识别的主要技术，主要是倒频谱矩归一化法、直方图均衡化方法、调频谱归一化方法以及它们的改进算法。这些算法都有各自的优势和待改进的地方，但总体来讲，它们都能在一定程度上消除或补偿了噪声带来的环境不匹配，较大幅度地提高识别器的性能。在实际应用中要根据具体需要，选用不同的归一化方法。此外，特征归一化技术还可以和一些后端处理技术相结合，如声学模型自适应技术(Model Adaptation)[36-37]和不确定译码(Uncertainty Decoding)[38-41]等，达到更好的补偿效果，进而更有效地提高识别系统的性能。

[1] Y. F. Gong. Speech recognition in noisy environments: A survey [J]. Speech Communication, 1995, 16: 261-291.

[2] S. Boll. Suppression of acoustic noise in speech using spectral subtraction [J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1979, 27 (2): 113-120.In: Proceedings of IEEE International Conference on Acoustics, Acoustics and Signal Processing

[3] K. Paliwal and A. Basu. A speech enhancement method based on Kalman filtering [C]//Proceedings of 1987 IEEE International Conference on Acoustics, Acoustics and Signal Processing. Dallas, Texas, USA，1987：177-180.

[4] Y. Ephraim and H. L. Van Trees. A signal subspace approach for speech enhancement [C]//Proceedings of 1993 IEEE International Conference on Acoustics, Acoustics and Signal Processing. Minneapolis, MN, USA，1993：355-358.

[5] H. Lev-Ari, Y. Ephraim. Extension of the signal subspace speech enhancement approach to colored noise [J]. IEEE Signal Processing Letters, 2003, 10 (4): 104-106.

[6] S. Furui. Cepstral analysis technique for automatic speaker verification [J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1981,29(2): 254-272.

[7] O. Viikki and K. Laurila. Cepstral Domain Segmental Feature Vector Normalization for Noise Robust Speech Recognition [J]. Speech Communication, 1998,25:133-147.

[8] A. de la Torre, A. M. Peinado, J. C. Segura et al. Histogram equalization of speech representation for robust speech recognition [J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 2005,13(3):355-366.

[9] S. H. Lin, Y. M. Yeh, and B. Chen. A Comparative Study of HEQ for Robust speech recognition [J]. International Journal of Computational Linguistics and Chinese Language Processing, 2007, 12 (2): 217-238.

[10] J. L. Gauvain and C. H. Lee. Maximum a posteriori estimation for multivariate Gaussian mixtureobservations of Markov chains [J]. IEEE Transactions on Speech and Audio Processing, 1994, 2 (2): 291-298.

[11] C. J. Leggetter and P. C. Woodland. Maximum Likelihood Linear Regression for Speaker Adaptation of Continuous Density Hidden Markov Models [J]. Computer Speech and Language, 1995, 9 (4): 806-814.

[12] J. Droppo. Noise Robust Automatic Speech Recognition[DB/OL].http://www.e eurasip.org/Proceedings//Eusipco/Eusipco2008/tutorials/tutorial_3_droppo.pdf, 2008-08-15.

[13] R. Togneri, A. M. Toh and S. Nordholm. Evaluation and Modification of Cepstral Moment Normalization for Speech Recognition in Additibe Babble Ensemble [C]//Proceedings of the 11th Australian International Conference on Speech Science & Technology. New Zealand，2006: 94-99.

[14] H.G. Hirsch and D. Pearce. The Aurora Experimental Framework for the Performance Evaluation of Speech recognition [C]//Proceedings of ISCA ITRW ASR2000. Paris, France，2000: 181-188.

[15] A. Acero and X. Huang. Augmented Cepstral Normalization for Robust Speech Recognition [C]//Proc. of IEEE Automatic Speech Recognition Workshop. Snowbird, Utah, USA: 1995.

[16] P. Jain and H. Hermansky. Improved mean and variance normalization for robust speech recognition [C]//Proceedings of 2001 IEEE International Conference on Acoustics, Acoustics and Signal Processing . Salt Lake City, Utah,USA: 2001.

[17] C. W. Hsu and L. S. Lee. Higher order cepstral moment normalization (HOCMN) for robust speech recognition [C]//Proceedings of 2004 IEEE International Conference on Acoustics, Acoustics and Signal Processing. Montreal, Canada: 2004: 197-200.

[18] Y. H. Suk, S. H. Choi and H. S. Lee. Cepstrum third-order normalisation method for noisy speech recognition [J]. IEEE Electronics Letters, 35(7): 527-528.

[19] S. Dharanipragada and M. Padmanabhan. A nonlinear unsupervised adaptation technique for speech recognition [C]//Proceedings of The 6th International Conference on Spoken Language Processing. Beijing, China，2000: 556-559.

[20] A. de la Torre, J. C. Segura, C. Benitez et al. Non-linear transformations of the feature space for robust speech recognition [C]//Proceedings of 2002 IEEE International Conference on Acoustics, Acoustics and Signal Processing. Orlando, FL, USA，2002: 401-404.

[21] S. Molau, D. Keysers and H. Ney. Matching training and test data distributions for robust speech recognition [J]. Speech Communication, 2003, 41(4): 579-601.

[22] C. Y. Wan and L. S. Lee. Joint Uncertainty Decoding (JUD) with Histogram-Based Quantization (HQ) for Robust and/or Distributed Speech Recognition [C]//Proceedings of 2006 IEEE International Conference on Acoustics, Acoustics and Signal Processing. Toulouse, France，2006: 125-128.

[23] C. Y. Wan and L. S. Lee. Histogram-based quantization (HQ) for robust and scalable distributed speech recognition [C]//Proceeding of 9th European Conference on Speech Communication and Technology. Lisbon, Portugal，2005: 957-960.

[24] M. Skosan and D. Mashao. Matching feature distributions for robust speaker verification [C]//Proceedings of Annual Symposium of Pattern Recognition Association of South Africa. Grabouw, South Africa，2004: 93-97.

[25] F. Hilger and H. Ney. Quantile Based Histogram Equalization for Noise Robust Speech Recognition [C]//Proceedings of the 7th European Conference on Speech Communication and Technology. Aalborg, Denmark，2001: 1135-1138.

[26] F. Hilger, S. Molau and H. Ney. Quantile Based Histogram Equalization For Online Applications [C]//Proceedings of the 7th International Conference on Spoken Language Processing. Denver, Colorado, USA，2002: 237-240.

[27] F. Hilger and H. Ney. Quantile based histogram equalization for noise robust large vocabulary speech recognition [J]. IEEE Transactions on Acoustics, Speech and Signal Processing,2006,14(3):845-854.

[28] J. Du and R. H. Wang. Cepstral shape normalization (CSN) for robust speech recognition [C]//Proceedings of 2008 IEEE International Conference on Acoustics, Acoustics and Signal Processing. Las Vegas, NV, USA，2008: 4389-4392.

[29] S. Gazor and W. Zhang. Speech probability distribution [J]. IEEE Signal Processing Letters, 2003, 10 (7): 204-207.

[30] K. Kokkinakis and A. K. Nandi. Speech Modelling Based On Generalized Gaussian Probability Density Functions [C]//Proceedings of 2005 IEEE International Conference on Acoustics, Acoustics and Signal Processing. Philadelphia, USA，2005: 381-384.

[31] B. Liu, L. R. Dai et al. Double Gaussian based feature normalization for robust speech recognition [C]//Proceedings of 4th International Symposium on Chinese Spoken Language Processing. Hong Kong, China，2004: 253-256.

[32] T. Houtgast and H. J. M. Steeneken. A review of the MTF concept in room acoustics and its use for estimating speech intelligibility in auditoria [J]. The Journal of the Acoustical Society of America, 1985, 77 (3): 1069-1077.

[33] X. Xiao, E. S. Chng and H. Li. Temporal Structure Normalization of Speech Feature for Robust Speech Recognition [J]. IEEE Signal Processing Letters, 2007, 14 (7): 500-503.

[34] X. Xiao, E. S. Chng and H. Li. Normalizing the speech modulation spectrum for robust speech recognition [C]//Proceedings of 2007 IEEE International Conference on Acoustics, Acoustics and Signal Processing. Honolulu, HI, USA,2007: 1520-6149.

[35] C. A. Pan, C. C. Wang and J. W. Hung. Improved modulation spectrum normalization techniques for robust speech recognition [C]//Proceedings of 2008 IEEE International Conference on Acoustics, Acoustics and Signal Processing. Las Vegas, NV, USA,2008: 4089-4092.

[36] M. Matassoni, M. Omologoand and D. Giuliani. Hands-free speech recognition using a filtered clean corpus and incremental HMM adaptation [C]//Proceedings of 2000 IEEE International Conference on Acoustics, Acoustics and Signal Processing. Istanbul, Turkey,2000: 1407-1410.

[37] M.G. Rahimand and B.H. Juang. Signal bias removal by maximum likelihood estimation for robust telephone speech recognition [J]. IEEE Transactions on Speech and Audio Processing, 1996,4(1):19-30.

[38] J. Droppo, A. Acero and L. Deng. Uncertainty decoding with SPLICE for noise robust speech recognition [C]//Proceedings of 2002 IEEE International Conference on Acoustics, Acoustics and Signal Processing. Orlando, Florida,2002: 57-60.

[39] H. Liao and M. J. F. Gales. Joint uncertainty decoding for noise robust speech recognition [C]//Proceedings of The 9th European Conference on Speech Communciation and Technology. Lisbon, Portugal,2005: 3129-3132.

[40] H. Liao and M.J.F. Gales. Issues with uncertainty decoding for noise robust automatic speech recognition [J]. Speech Communication, 2008, 50 (4): 265-277.

[41] V. Stouten, H. Van hammeand and P. Wambacq. Model-based feature enhancement with uncertainty decoding for noise robust ASR [J]. Speech Communication, 2006, 48 (11): 502-1514.