甲骨拓片字形图像复原方法

顾绍通

(1. 徐州师范大学 语言研究所,江苏 徐州 221009；2. 语言科学与神经认知工程江苏省重点实验室，江苏 徐州 221009；3. 徐州师范大学 语言科学学院，江苏 徐州 221009)

1 引言

上个世纪以来，随着考古工作的深入开展，陆续出土了大量的古代珍贵文献，这些出土文献中有相当一部分是书写在龟甲和兽骨上面的，如甲骨文，是我国迄今发现的最早的一种成熟文字系统， 具有极其重要的学术价值和文化遗产保护价值。甲骨文是书写在龟甲和兽骨上的文字，由于龟甲和兽骨质地本身并非平滑如镜，又深埋地下经历了几千年的岁月沧桑，加上发掘和运输的污损，损坏已很严重，字形的边缘已经非常模糊，呈现出非常明显的锯齿形态。这样受污损的字形不利于甲骨文字形的进一步使用[1]。由于字形边缘已经变得非常模糊，对于甲骨文字形的识读和研究带来极大不便，因而非常需要对甲骨拓片上的字形进行复原。目前采用某些图像处理软件可以近似恢复甲骨文字形的原始面貌,但是涉及非常复杂的手工交互，而且需要具有丰富经验的专业人员操作，耗时耗力，修复效果也不如人意。目前已出现多种图像修复算法，如偏微分方程方法[2-3]、整体变分方法(Total Variational,TV)[4]、基于曲率的扩散模型(Curvature-driven Diffusion,CDD)[5]、基于高斯卷积核对图像滤波方法[6]、径向基函数方法(Radial Basis Functions,RBF)[7-8]、Mumford-Shah-Euler图像模型[9],纹理合成的方法[10]、基于数学形态学的方法[11]、基于Cahn-Hilliard方程的方法[12]、空间变量高斯尺度混合的方法[13]、机器学习方法[14]、基于小波拉普拉斯变换的方法[15]、基于近邻像素相关函数和边缘检测的图像平滑细化方法[16]等。以上方法均采用图像处理的方法修复破损区域,并没有分析噪声区域的统计特征，而且对于像甲骨拓片这种书写材料比较特殊、污染原因多样化以及埋藏时间漫长的字形图像缺乏针对性，修复效果也难以如意。

本文针对出土甲骨拓片上字形的特点，采用基于自适应阈值和分形几何(Fractal Geometry)的方法对甲骨拓片上的字形进行计算机辅助复原。通过对甲骨拓片上高斯噪声进行Bayes估计，计算噪声区域的自适应阈值，对噪声区域进行填充，进而去除拓片图像中的噪声区域。然后计算拓片上字形图像边缘的分形维数，对字形图像的边缘进行压缩变换，平滑字形图像边缘因腐蚀所造成的凹凸形态。

文章其余部分的组织结构如下：第二节分析了甲骨拓片字形图像的特征，介绍了基于自适应阈值的修复方法；第三节叙述了分形几何以及压缩变换的原理；第四节是实验结果示例，并对实验结果进行了分析；第五节对全文进行总结。

2 基于自适应阈值的区域填充方法

2.1 甲骨拓片字形图像分析

甲骨文是契刻在龟和兽骨上的文字，因而字形的笔划线条具有以下特点[17]：构成甲骨文的线条多为直线，且线条瘦劲挺直，两端尖锐，转折处往往以两条直线相接成屈折状。甲骨拓片在地下深埋上千年，由于受到腐蚀、发掘损坏以及拓片质地本身等原因，导致甲骨拓片有许多噪声点，如图1、图2所示。图3 为经过二值化处理的甲骨拓片图像，图4是甲骨拓片字形图像的轮廓图。甲骨拓片上的噪声点具有如下特点：(1)噪声区域的亮度低于甲骨文字形笔划的亮度；(2)噪声区域呈离散状态，连通区域面积较小，区域面积呈正态分布。相比之下，甲骨拓片上字形图像的特征有：(1)分形：甲骨拓片在地下深埋上千年，由于受到腐蚀，甲骨文字形图像边缘部分与整体具有相似性，具备分形特征，如图4所示； (2)笔划区域连通性：甲骨文字形的笔划一般是单连通区域，个别笔段会出现断裂；(3)像素值空间的聚敛性：甲骨文字形笔划的像素亮度较高，而且比较连续，且在某个像素值区域比较集中。

图1 《甲骨文合集》559(正面)

图2 《甲骨文合集》559正之局部放大

图3 经过二值化处理的甲骨拓片图像

图4 轮廓图

2.2 基于Bayes估计的自适应阈值

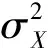
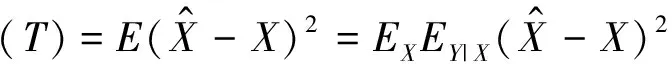
(1)

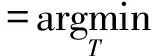
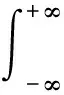
(2)

其中，

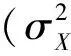
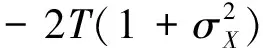
标准密度函数

从而得

(3)

TB(σX)是对T*的一个近似，最大偏差不超过1%。下面来估计式(3)中的参数。

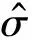
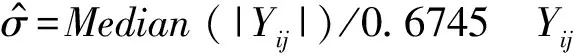
(4)

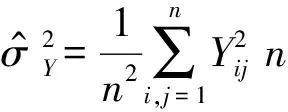
(5)

(6)

因此得到数据驱动的、基于子带的自适应阈值：

(7)

这里的阈值公式(7)在MSE意义上是近优的，其去噪效果与SURE阈值法相当，但计算量要比SURE阈值法小得多。

甲骨拓片图像中的噪声是由于受到腐蚀、发掘损坏以及拓片质地本身等原因产生的，噪声区域具有区域面积小、正态分布等特点，通过计算自适应阈值，将噪声区域面积和阈值进行对比，将小于阈值的噪声区域视为噪声，对其进行填充。

3 基于分形几何的字形图像复原方法

3.1 分形几何理论

分形是20世纪70年代初由Mandelbrot[18]引入的关于自相似性的一般概念,是描述具有相似结构的几何形状的工具,后来发展成对各种复杂系统的自相似性进行研究的工具。具有分形特征的表面具有自相似性,n维欧氏空间中的有界集合A, 若A可以表示为其自身Nr个互不覆盖的子集的并时, 则A是自相似的。此时,A的分形相似维数D定义为

其中,r是所有坐标方向上的尺度因子,Nr是有界集合A的互不覆盖的子集个数。对于图像而言, 把二维图像视作一个三维空间中的一个表面(x,y,f(x,y)), 其中f(x，y)为图像(x,y)位置处的灰度值, 于是图像灰度的变化情况将反映在该表面的粗糙程度上, 使用不同尺度去度量该表面, 得到的维数就是图像的分形维数。目前已有许多估计其分形维数的方法, 例如频域方法[19]、计盒维数法[20]、数学形态学的方法[11]、网格计数法[21]、差分盒维数算法(Differential Box Counting,DBC)[22-23]等。其中,差分盒维数法由于易于计算,性能较好等优点,在实际中得到了广泛的应用。

差分盒维数法的主要思想是:将m×n大小的图像分割成s×s的子块,s是介于 1 和m/2之间的一个整数。令r=s/m, 将图像视为一个三维空间中的一个表面(x,y,f(x,y)),(x,y)表示像素点的平面位置, 第三维用来表示像素点的灰度值f(x，y)。平面被分割成许多s×s的网格,在每个网格上, 是一列s×s×s的盒子。假设在图像的第(i,j)个网格内图像灰度的最高值和最低值分别落在第l个和第k个盒子内, 则Nr在第(i,j)个网格内的分布nr(i,j)为

nr(i,j)=l-k+1

nr(i,j)是覆盖第(i,j)网格中的图像所需的盒子数,则覆盖整个图像所需的盒子数Nr为

(i,j)

对于不同的r, 可以得到不同的Nr值, 采用最小二乘法可以拟合出lgNr～lg(1/r)的斜率, 即可得到对应的分形维数值D。

3.2 甲骨拓片字形图像边缘的分形特征

甲骨拓片在地下深埋上千年，由于受到腐蚀，字形边缘呈现出连绵起伏的锯齿形状。甲骨文字形图像的锯齿形状边缘部分与整体具有相似性，具备分形特征,如图5所示。

图5 图4图像之局部放大

构成甲骨文字形的笔画多为直线，由于甲骨拓片受到腐蚀，字形图像边缘呈现凹凸不平连绵起伏的锯齿形状，和海岸线的形状特征是非常相似的。字形图像边缘可以通过分形压缩变换进行平滑，从而改善甲骨拓片字形图像边缘的锯齿形状。

在平面欧氏空间中，伸缩变换可以表示为：

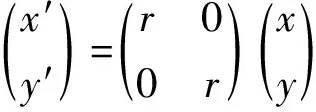
上式中，r为伸缩比，r大于1时为伸长变换，r小于1时为压缩变换。

在字形轮廓上取点P0、P1、P2…Pn，将字形轮廓等分为n个部分。Pil(xil,yil)、Pir(xir,yir)分别为轮廓段PiPi+1(i=0,1,…,n)的左端点和右端点，Pit(xit,yit)、Pib(xib,yib)分别为轮廓段PiPi+1(i=0,1,…,n)的上顶点和下顶点，对于轮廓段PiPi+1上任意一点Pi(xi,yi)，有xl≤xi≤xr，yb≤yi≤yt。Pij(xij,yij)、Pij+1(xij+1,yij+1)、Pij+2(xij+2,yij+2)、Pij+3(xij+3,yij+3)、Pij+4(xij+4,yij+4)、Pij+5(xij+5,yij+5)为PiPi+1上的局部极值点。直线L是过PibPit中点且平行于x轴的直线。左端点、右端点、上顶点、下顶点以及局部极值点称为轮廓的特征点，对这些特征点进行压缩变换后得到图6中的虚线部分，这是伸缩比为1/2、1/4时压缩变换后得到的曲线。可以看出，经过压缩变换后，图像边缘趋于平滑。图6显示的是L与x轴平行的情况，L与y轴平行时的情况可以仿此。

图6 字形轮廓的特征点及压缩变换后的曲线

经过统计，甲骨拓片字形图像边缘的分形维数在1.2～1.3之间，设定分形维数阈值T，当压缩变换后的图像分形维数小于T时，处理结束。直线的分形维数是1，通常，甲骨拓片字形图像分形维数阈值设为1.05即可。

算法步骤如下：

Step1 使用freeman链码对输入图像f(x,y)进行轮廓跟踪。

Step2 在x和y方向上对f(x,y)进行压缩变换，得到图像f′(x,y)。

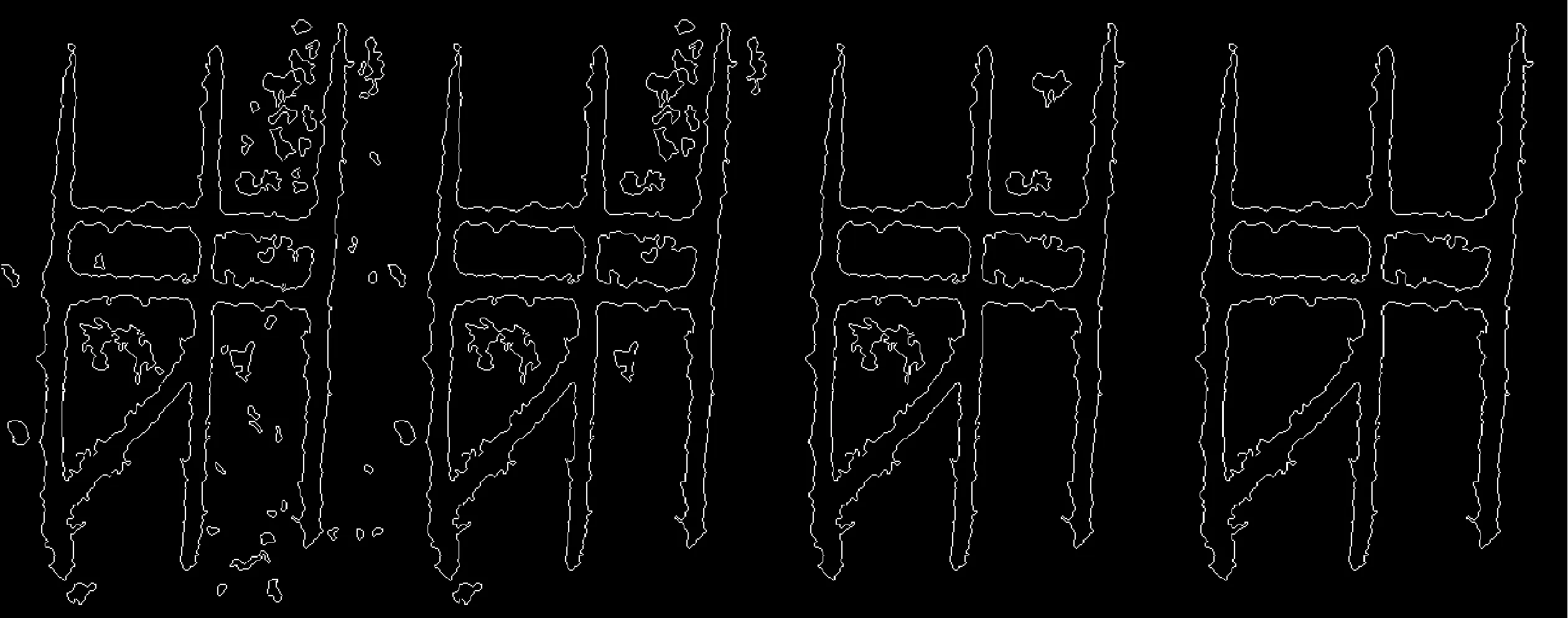
Step3 计算图像f′(x,y)的分形维数D，如果D

算法流程图如图7所示。

图7 算法流程图

4 实验和分析

我们在Apple Mac Pro工作站上在Windows环境下，用Visual C++和OpenCV实现了上述所有算法。图8是经过面积阈值处理后的图像，图9是分形维数阈值分别为1.2、1.1、1.05时经过压缩变换后的图像。可见，图像经过压缩变换后，图像边缘由分形产生的锯齿状态得到了平滑。分形维数阈值越低，平滑的效果越好，但是同时数据运算量也加大。

图8 面积阈值为10、20、30、40填充后的图像

图9 分形维数阈值分别为1.2、1.1、1.05时经过压缩变换后的图像

5 结论

甲骨文是我国迄今发现的最早的一种成熟文字系统，其本身具有极其重要的学术价值和文化遗产保护价值。如何借助先进的计算机技术对中国最早的成熟文字——甲骨文进行数字化,展示以及有效保护和方便使用，具有重要的现实意义。本文分析了甲骨文拓片中噪声的特点以及字形图像边缘的分形特征，提出了一种基于自适应面积阈值和分形几何的甲骨拓片字形图像复原方法。通过Bayes风险函数来估计甲骨拓片上噪声区域面积的优化阈值，对噪声区域进行填充，从而去除拓片中的背景噪声。采用统计的方法计算甲骨拓片字形图像边缘的分形维数，对甲骨拓片字形图像的边缘进行基于数学分形的压缩变换操作，进而对甲骨拓片上甲骨文字形图像边缘进行平滑，改善甲骨文拓片图像边缘的锯齿形态。实验结果显示，这一方法的图像修复效果是比较明显的。

[1]顾绍通，马小虎，杨亦鸣.基于字形拓扑结构的甲骨文输入编码研究[J].中文信息学报，2008，22(4):123-128.

[2]M. Bertalmio, G. Sapiro, V. Caselles, et al. Image inpainting[C]//Proceedings of SIGGRAPH 2000. New Orleans, USA, 2000:417-424.

[3]M. Bertalmio, A. L. Bertozzi, G. Sapiro, et al. Navier-stokes, fluid dynamics, and image and video inpainting[C]//Proceedings of the International Conference on Computer Visionand Pattern Recognition, Kauai, HI, 2001, I, 355-362.

[4]T. Chan, J. Shen. Mathematical Models for Local Deterministic Inpaintings[P]. TR00-11, Department of Mathematics, University of California-Los Angeles, Los Angeles, Califormia, USA, 2000.

[5]T. Chan, J. Shen. Non-Texture Inpainting by Curvature-Driven Diffusions[P]. TR00-35. Department of Mathematics, University of California-Los Angeles, Los Angeles, Califormia, USA, 2000.

[6]M. Oliveira, B. Bowen, R. McKenna, et al. Fast digital image inpainting[C]//Proceedings of the Visualization, Imaging, and Image Processing IASTED Conference. Marbella, Spain, 2001:261-266.

[7]J. C. Carr, R. K. Beatson, J. B. Cherrie, et al. Reconstruction and representation of 3D objects with radial basis functions[C]//Proceedings of ACM SIGGRAPH 2001, Los Angeles, California, USA, 2001:67-76.

[8]J. C. Carr, W. R. Fright. Beatson R K.. Surface interpolation with radial basis functions for medical imaging[J]. IEEE Transactions on Medical Imaging, 1997,16(1):96-107.

[9]S. Esedoglu and J. Shen. Digital inpainting based on the Mumford-Shah-Euler image model[J]. Eur. J. Appl. Math., 2002,13(4):353-370.

[10]A. Criminisi, P. Perez, K. Toyama. Object removal by exemplar-based inpainting[C]//Proceedings of 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Madison, Wisconsin, 2003, 2:721-728.

[11]M. Elad, J. L. Starck, P. Querre, and D. L. Donoho. Simultaneous cartoon texture image inpaitning using morphological component analysis[J].Appl. Comput. Harmon. Anal., 2005, 19(3):340-358.

[12]A. Bertozzi, S. Esedoglu, and A. Gillette. Inpainting of binary image using the Cahn-Hilliard equation[J]. IEEE Transactions on Image Processing, January 2007, 16(1):285-291.

[13]J. A. Guerrero-Colón, L. Mancera, and J. Portilla. Image restoration using space-variant Gaussian scale mixture in overcomplete pyramids[J]. IEEE Transactions on Image Processing, January 2008, 17(1):27-41.

[14]Philippe Henri Gosselin and Matthieu Cord. Active Learning Methods for Interactive Image Retrieval[J]. IEEE Transactions on Image Processing, July 2008, 17(7):1200-1211.

[15]Julia A. Dobrosotskaya and Andrea L. Bertozzi. A Wavelet-Laplace Variational Technique For Image Deconvolution and Inpainting[J]. IEEE Transactions on Image Processing, May, 2008, 17(5):657-663.

[16]唐松，郭椿标，郑南宁.基于文字结构特征的快速平滑细化方法[J].中文信息学报，1990，4(2)：49-54.

[17]马小虎，黄文帆，顾绍通，杨亦鸣.甲骨文点阵字形转换为甲骨文轮廓字形的方法[J]．语言科学，2004，3(3)：3-11．

[18]B. B. Mandelbrot. Fractals:Form, Chance and Dimension[M]. San Francisco:W. H. Freeman & Co., 1977.

[19]A. P. Pentland. Fractal-Based Description of Natural Scenes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984, 6(6):661-674.

[20]Chaudhuribb, N. Sarkar, Texture segmentation using fractal dimension[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, vol. 17(1):72-77.

[21]J. Gangepain, C. Roques-Carmes. Fractal approach to two dimensional and three dimensional surface roughness, Wear, 1986,109(1-4):119-126.

[22]N. Sarkar, Chaudhuribb. An efficient differential box-counting approach to compute fractal dimension of image[J]. IEEE Transactions on System Man and Cybernet. 1994, 24(1):115-120.

[23]N. Sarkar, Chaudhuribb. An efficient approach to estimate fractal dimension of texture images[J]. Pattern Recognition, 1992, 25(9):1035-1041.