基于摇杆-转向架机构星球探测车的越障分析

汪丽芳 余晓流, 汪永明,2 高文斌 王洪光 王越超

1.安徽工业大学,马鞍山,243002 2.东南大学,南京,211189 3.中国科学院沈阳自动化研究所机器人学国家重点实验室,沈阳,110015

0 引言

自20世纪60年代以来,国外已经研制了许多星球探测机器人。根据机器人移动机构的特点,星球探测机器人的驱动方式可分为轮式、腿式、轮腿式和履带式[1-3]。由于轮式移动系统在相对平坦的地形中运行速度快,且控制较简单,故大多数研究者都倾向于将探测车的移动系统设计成轮式结构。目前轮式星球探测车有单轮、四轮、六轮和八轮等结构。其中,采用摇臂-转向架结构的六轮式移动系统具有较强的适应性和越障能力[4]。Rocky系列火星漫游车以及Sojourner火星探测车就采用此种结构形式。

文献[5]用静力学方法对车体受力进行分析,建立了在约束条件下摇臂-转向架的受力方程。由于该方程是通过对车体在平面地形的受力进行分析而建立的,故不能作为越障分析数学模型。

本文建立了考虑横滚角θ和俯仰角φ时的车体的受力方程,指出当车轮所受摩擦力可行域不存在时,机构将不具有初始条件下的越障能力,并对机构右侧各轮在具有坡度地面上单独前进越障进行了仿真。

1 机构受力分析

1.1 机构简介

基于摇杆-转向架机构的六轮移动机构原理图如图1所示。其六轮安装在关节支架上,均为独立驱动。两侧支架上的摇杆一端直接与后轮连接,另一端与二级摇杆(转向架)连接。在摇杆与转向架之间为自由铰连接,转向架两端各连接一驱动轮。两摇杆采用差动铰与箱体连接,这使得箱体的俯仰角φ为两摇杆倾角的平均值[6]。

1.2 坐标系的建立

图1 摇杆-转向架移动机构原理及机构参数

如图1所示,探测小车的坐标系原点O选在右后轮腿回转中心处。设两边的摇杆和转向架与水平方向的夹角分别为 θ1、θ2、θ3和 θ4,其大小由差动铰和自由铰的位移决定,可由逆向运动学求得[5]。设箱体的横滚角、俯仰角和偏航角分别为θ和φ和ψ。参数ψ为沿竖直方向的转角,即车体的偏航角。由于机构的对称性,为方便起见,在对机构力学分析时,假设其取值为零。其余机构的结构参数如图1所示。各轮的中心坐标为(xi,yi,zi),i分别为 ar、mr、f r、al、ml、f l,a、m 、f、r、l,分别代表后轮、中轮、前轮以及右侧、左侧。

1.3 差动铰的受力

假设箱体除与差动铰的作用力外,只受重力的作用。设初始状态时,箱体重心相对于两差动铰中心的位置坐标为(x b,y b,z b)。图2为箱体与两边摇杆在差动铰处的受力分析图。摇杆与箱体通过差动铰固连,因此可传递x向、y向、z向的力和力矩 , 分 别 记 为Mry、Mrz、Mlx、Mly和Mlz,G为箱体所受重力,力矩计算参考旋转中心点如图2所示。根据箱体的受力平衡可列出下列方程：

(a)箱体在差动铰处的受力分析

图2 机构受力图

x向力：

y向力：

z向力：

x向力矩：

y向力矩：

z向力矩：

根据差动铰传递的力矩平衡可得

车体在运动时,地面对车轮的作用力只需平衡重力和前进过程所需要的水平方向力,所以假设车轮的受力为竖直方向的力Fi和沿水平方向力,竖直方向的力Fi可以分解为沿摇杆-转向架平面内的力和沿车轮法向的力。

设摇杆右差动铰处的受力为

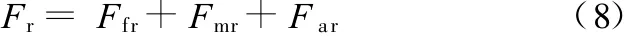
式中,Ffr为摇杆右侧前轮对差动铰作用力分量;Fmr为摇杆右侧中轮对差动铰作用力分量;Far为摇杆右侧后轮对差动铰作用力分量。

摇杆左差动铰处的受力为

式中,Ffl为摇杆左侧前轮对差动铰作用力分量;Fml为摇杆左侧中轮对差动铰作用力分量;Fal为摇杆左侧后轮对差动铰作用力分量。

根据力平衡可得

由于机构的复杂性,F r和F l的作用点难于确定,需要根据变形协调条件求解,这将会使其计算特别繁杂。在力作用点未知的情况下,假设Fr和F l的作用点分别为每边三轮中心所连三角形的重心处,由此带来的实际力作用点的偏离量最小,根据两边摇杆-转向架机构y向力平衡以及x向力矩平衡可得

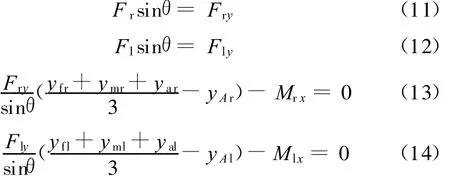
式中,下标A表示差动铰的中心。

根据整车在 x向的力矩平衡可得

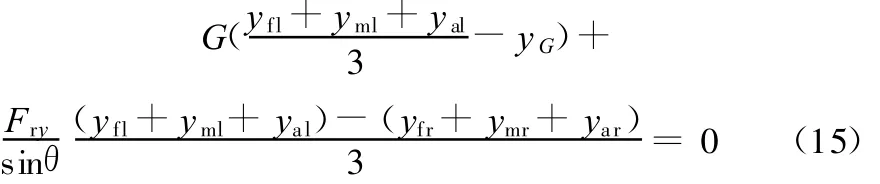
式中,yG为箱体重心在参考坐标系F下的y轴坐标。

联立式(2)、式(13)、式(14)和式(15),可以求出 Fry、Fly、Mrx和 Mlx。

为简化起见,不考虑车轮方向控制误差带来切向力的影响,即认为两边摇杆-转向架机构所在平面不受地面摩擦力产生的z向力矩。鉴于此,可得M r z=M l z=0。因此,根据式(1)和式(6)可求出F r x和F l x;由式(5)和式(7)可以求出M r y和Mly;由式(3)和式(4)可以求出Frz和Flz。至此,差动铰受力的12个未知数全部求出。

1.4 车轮与地面间的受力分析

取摇杆-转向架所在平面进行受力分析(不考虑法向摩擦力对越障能力的影响)。由于两边摇杆-转向架机构完全相同,仅关节位移与受力的大小不同,因此,其力学模型完全一致。仅以右边为例进行分析。受力图如图3所示。

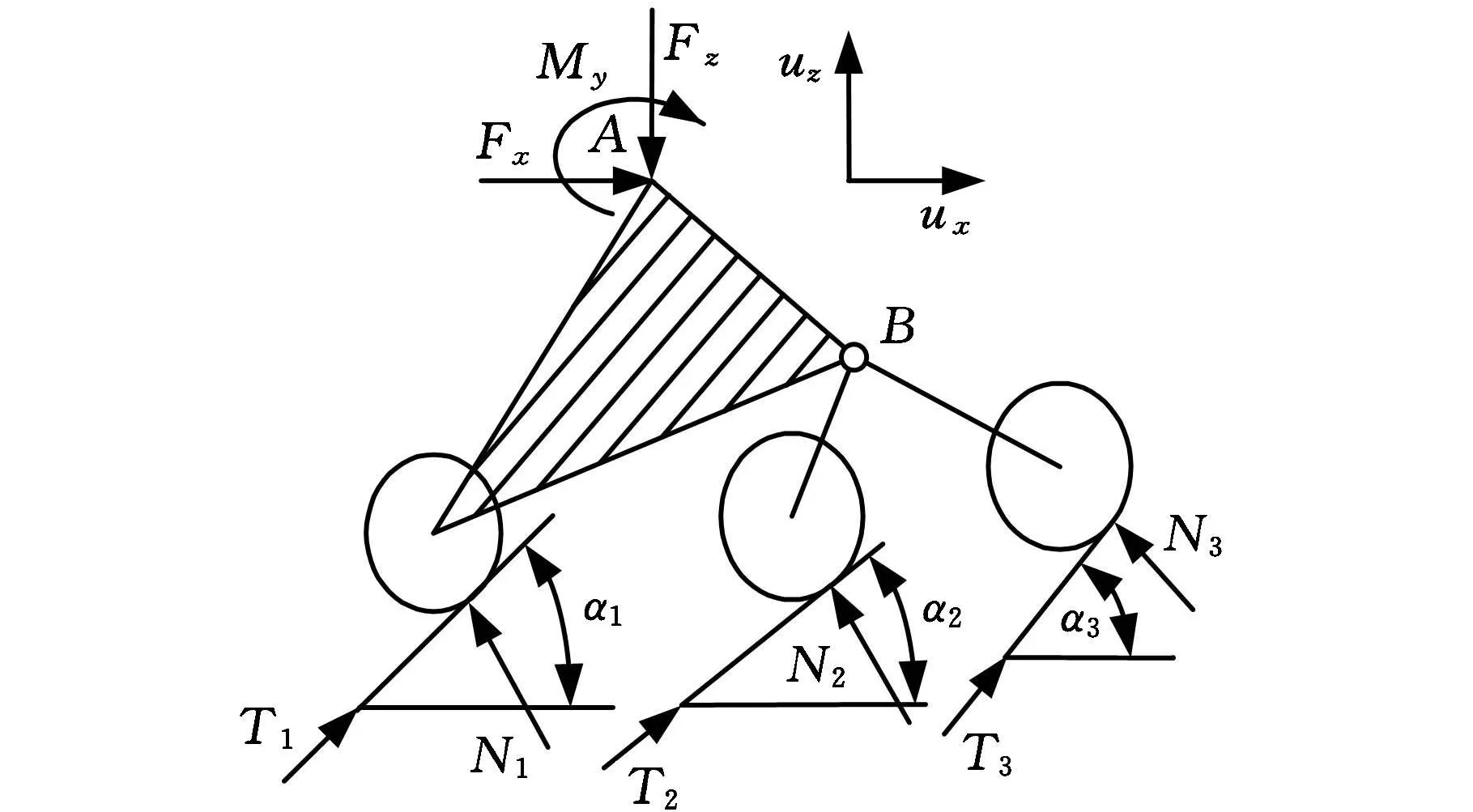
图3 车轮与地面间的受力分析

假设车轮与地面点接触,接触点处的切线与地面的夹角分别为 α1、α2和 α3,车轮半径为 r,地面给予车轮的法向支持力分别为 N1、N2和N3,切向摩擦力分别为T1、T2和T3,摩擦因数为μ。支持力与摩擦力的约束条件为

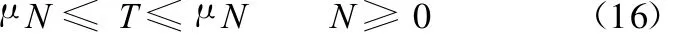
根据x向、z向受力平衡,可以列出下列方程：

根据平面内机构所受y向整体力矩平衡可得

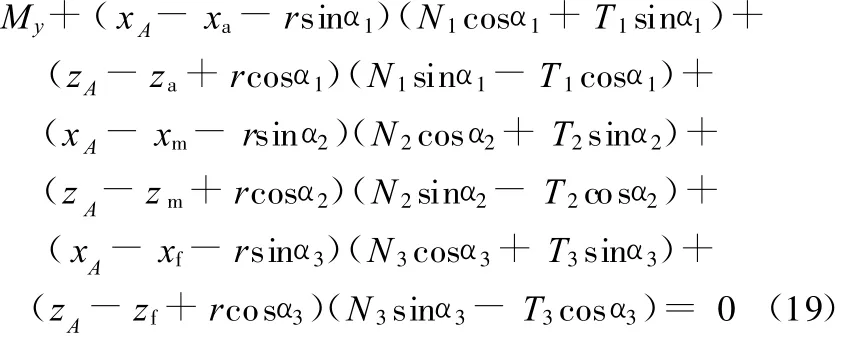
由于B点为自由铰,不能传递y向转矩,根据中轮、前轮在B点的转矩守恒可得

在图3所示的受力中,有6个未知数,但只有4个平衡方程,因此不具有唯一解。

2 越障能力分析

2.1 越障约束

车轮能够越障的前提条件为车轮驱动电机在不超过过载转矩的情况下爬上障碍物,即

由于摩擦力受到摩擦因数的限制,所以有一定的最大取值,并对应于最大转矩,当设计时按最大转矩选取电机即可不考虑电机转矩的约束。

2.2 越障能力

车轮具有越障能力,即式(17)～式(20)在满足式(16)、式(21)的约束条件时存在有理解。式(17)～式(20)为一非齐次线性方程组：

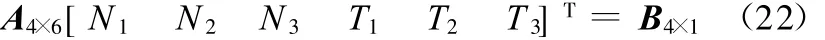
当矩阵A的秩等于4时,式(22)具有二维解空间。可以设2个摩擦力为解空间的变量,通过约束条件找出解空间的可行域,当左边或右边可行域不存在时,机构将不能在所给定的初始条件下平衡,即不具有初始条件下的越障能力。

2.3 仿真步骤

MATLAB程序仿真步骤见图4。

图4 越障分析仿真步骤

2.4 算例

图1 所示的机构参数见表1。

表1 机构参数 mm

箱体重心相对于两差动铰中心的位置坐标为 xb=50mm、yb=0、zb=100mm。由于机构的对称性,为方便起见,取车体的偏航角ψ=0。箱体的俯仰角 φ=γ-(θ1+θ3)/2。其中 ,γ为θ1与θ3的初始转角。

2.4.1 仅右前轮越障

当给定车轮z坐标分别为(由右至左,由后至前)[0 0 250 0 0 0]mm,车轮与地面的接触角取为[0 0 45 0 0 0](°)时,摩擦力 T r1、T r2、T r3 以及Tl1、Tl2、Tl3的关系如图5所示。从图5可以看出,右边机构的可行域减小,且向正向移动。

图5 仅右前轮越障时的受力情况

2.4.2 仅右中轮越障

当给定车轮z坐标分别为(由右至左,由后至前)[0 250 0 0 0 0]mm,车轮与地面的接触角取为[0 45 0 0 0 0](°)时,摩擦力 T l2、T l3以及 T r2、T r3的关系如图6所示。从图6可以看出,右边机构的可行域减小,且向正向移动。

2.4.3 仅右后轮越障

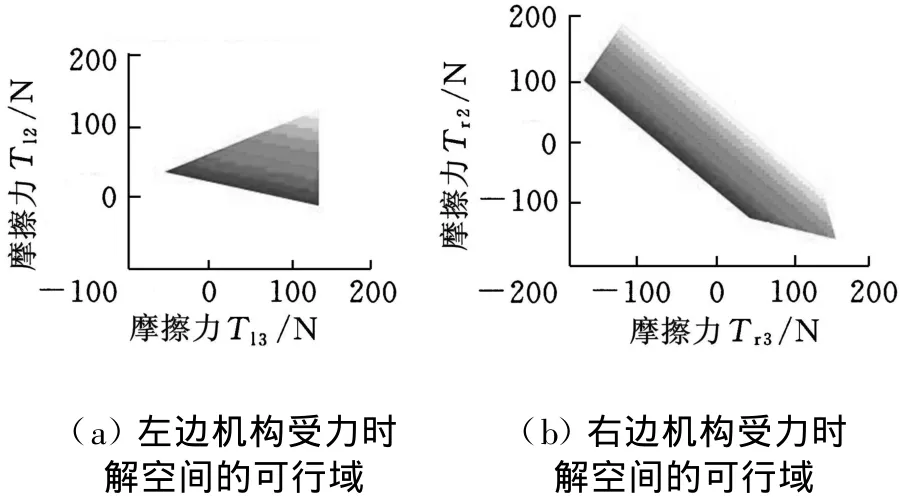
图6 仅右中轮越障时的受力情况

当给定车轮z坐标分别为(由右至左,由后至前)[250 0 0 0 0 0]mm,车轮与地面的接触角取为[45 0 0 0 0 0](°)时,摩擦力 Tr2、Tr3以及 Tl2、Tl3的关系如图7所示。

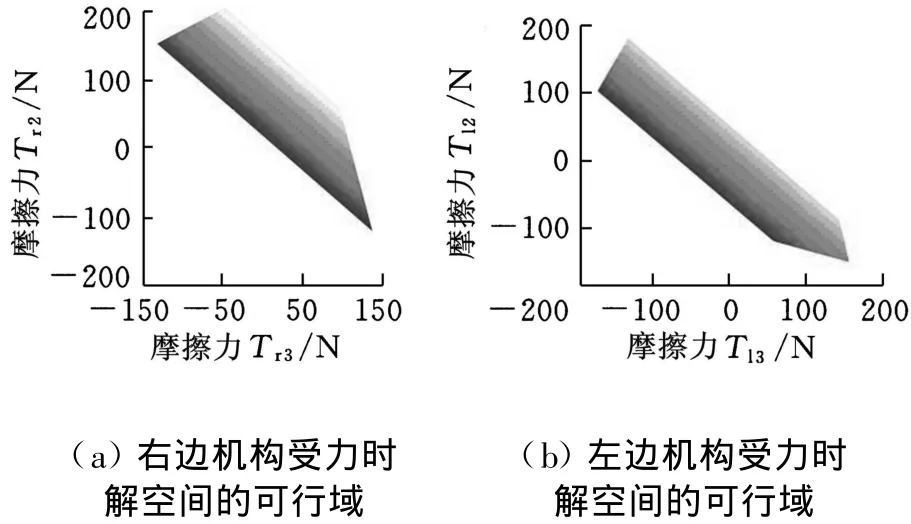
图7 仅右后轮越障时的受力情况

3 结束语

用静力学方法找出了在约束条件下车轮所受摩擦力的解空间可行域。通过解空间可行域考察了机构的越障能力。当可行域不存在时,机构将不能在给定的初始条件下平衡,即不具有初始条件下的越障能力。在前进的过程中,相同的越障高度以及与地面相同的接触角下,后轮的越障能力最强(解空间的可行域最大),中轮最差,前轮适中。

本文的研究成果为基于六轮遥感转向架星球探测车在松软地面环境作业运动控制方案的设计奠定了理论基础。

[1] 刘方湖,陈建平,马培荪,等.行星探测机器人的研究现状和发展趋势[J].机器人,2002,24(3)：268-8.

[2] Wang Yongming,Yu Xiaoliu,Tang Wencheng.A New-type Wheel-legged Lunar Rover and its Mobile Performance Analysis[C]//Proceedings of 2009 International Conference on Mechanical and Electrical Technology.New York：ASME,2009：31-36.

[3] Shang J,Luo Z,Fan D,et al.A Six Wheeled Robot with Active Self-adaptive Suspension for Lunar Exploration[C]//Proceedings of 2006 International Technology and Innovation Conference.Stevenage：United Kingdom,2006：2035-2038.

[4] 李海滨,段志信,康补晓.基于摇臂-转向架结构月球探测车的越障能力分析[J].重庆工学院学报,2005,19(11)：1-5.

[5] Hacot H,Dubowsky S,Bidaud P.Analysis and Simulation of a Rocker-Bogie Exploration Rover[C]//Proceedings of the Twelfth CISM-IFT.MM Symposium on Theory and Practice of Robots and Manipulators.Wien：Springer,1999.

[6] 郑文纬,吴克坚.机械原理[M].北京：高等教育出版社,2002.