磁悬浮系统结构静刚度与结构动刚度测量实验
刘小静 胡业发 张薇薇 魏 坚
武汉理工大学,武汉,430070
0 引言
有关磁力轴承刚度的特性与规律历来研究不多,对刚度的定义也还没有形成完全的界定,对于实验测定刚度的方法研究亦较少。清华大学的赵雷等[1]与上海大学的汪希平[2]在早期分别采用信号生成系统、信号测试分析系统和在外部激振的方式测得磁力轴承的动刚度和刚度-频率曲线,但是这些实验比较简单,对刚度的特性研究非常有限,并且大多研究将磁力轴承的刚度与阻尼等同于弹簧阻尼系统的刚度与阻尼[3],然而磁力轴承的刚度是由其结构、控制等多种因素决定的,不同于弹簧阻尼的由材料确定的材料刚度,故本文研究中的磁力轴承的刚度为结构刚度(以区别于普通刚度)。本文以磁悬浮盘片系统为实验对象,测量磁悬浮系统结构静刚度与结构动刚度,研究结构静刚度和结构动刚度的变化规律与特性,为支承特性理论提供实验依据。另外,本文比较了采用直接加载外力实验方法以及采用控制系统激励以模拟外力实验方法的实验结果,结果表明两种方法都可以测量系统刚度。
1 结构静刚度与结构动刚度定义
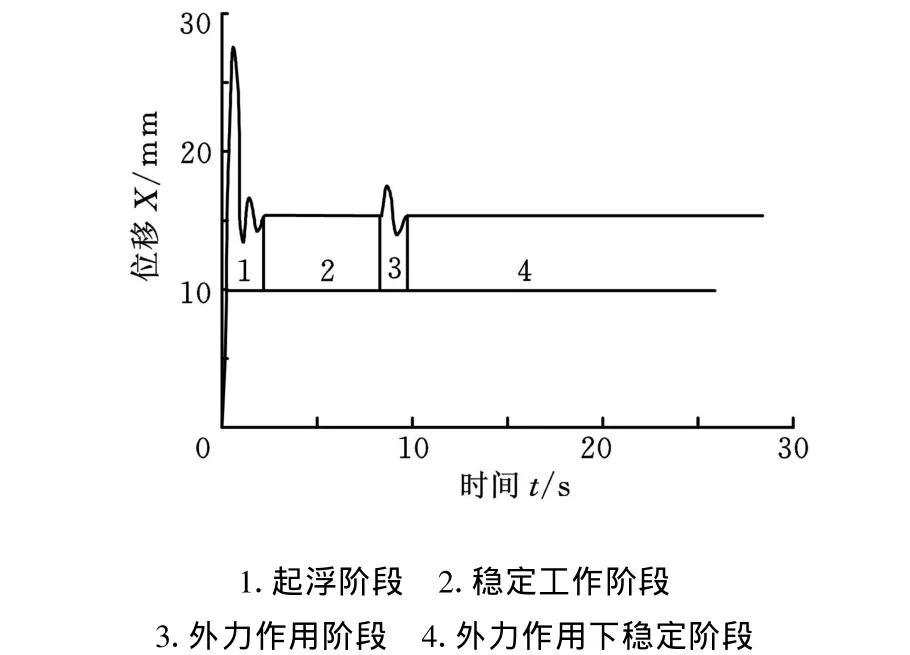
图1 单自由度磁悬浮系统转子位移阶段划分
单自由度磁悬浮系统转子的整个悬浮过程可以用图1所示转子的时间—位移曲线表示,分为4个阶段:起浮阶段、稳定工作阶段、外力作用阶段、外力作用下稳定阶段。其中外力作用阶段与外力作用下稳定阶段是磁力轴承主要工作状态,故结构动刚度与结构静刚度研究的是这两个阶段的磁力轴承抵抗变形的能力。将这两个阶段放大,得到如图2所示的位移曲线。
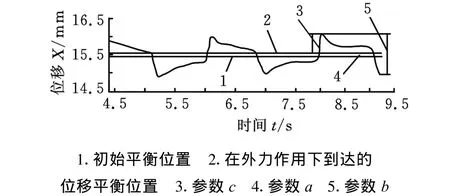
图2 磁力轴承单自由度外力作用下位移曲线
在外力作用下到达的位移平衡位置偏移初始平衡位置的偏差a=(c1+c2+…+ci)/i=Δx(时间采样点i=1,2,…,n);位移曲线最大峰值b=|c+max|+|c-max|;峰值偏离平衡位置的最大距离,也叫最大超调量cmax,是在一段采样时间内获得的最大数据(i=1,2,…,n)。
本文根据参数a、b、c定义磁力轴承结构静刚度与结构动刚度。在外力作用下的稳定工作阶段:磁力轴承结构静刚度
KJ=FW/a
在外力作用阶段:磁悬浮系统结构动刚度1
KD1=FW/Δx
磁悬浮系统结构动刚度2
KD2=FW/cmax
2 实验设备
本实验由磁悬浮盘片系统、B&K振动仪、万用表、砝码等组成,如图3、图4所示。各参数如表1所示。
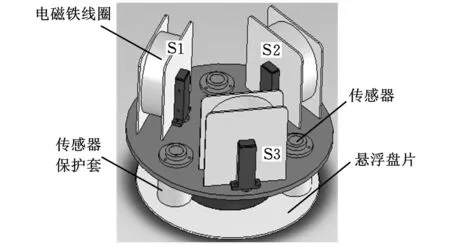
图3 磁悬浮盘片结构图

图4 磁悬浮盘片系统
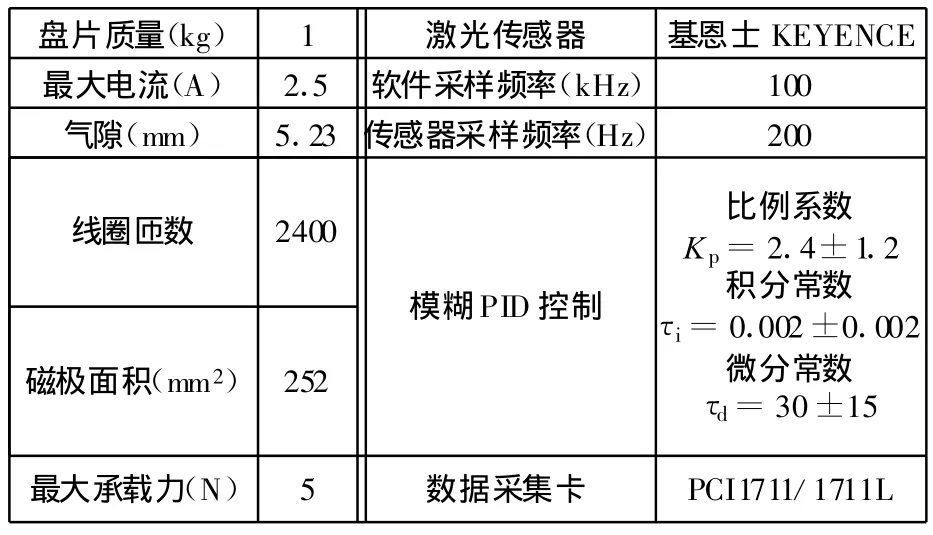
表1 实验平台各参数
忽略测量时的外界噪声干扰、基座振动干扰、盘片制造误差,以及加载位置的误差,且只采集一个盘片回路,即本实验只研究其中的S3位移值与电流值。
3 结构静刚度的测量
在盘片中心位置下方加载砝码,将传感器采集的位移信号转换成位移,将万用表测得的电压转换成电流,根据数据计算 c、b、a。绘制的外力-电流图、外力-位移曲线图、外力-动刚度2曲线图分别如图5、图6、图7所示。

图5 外力-电流曲线
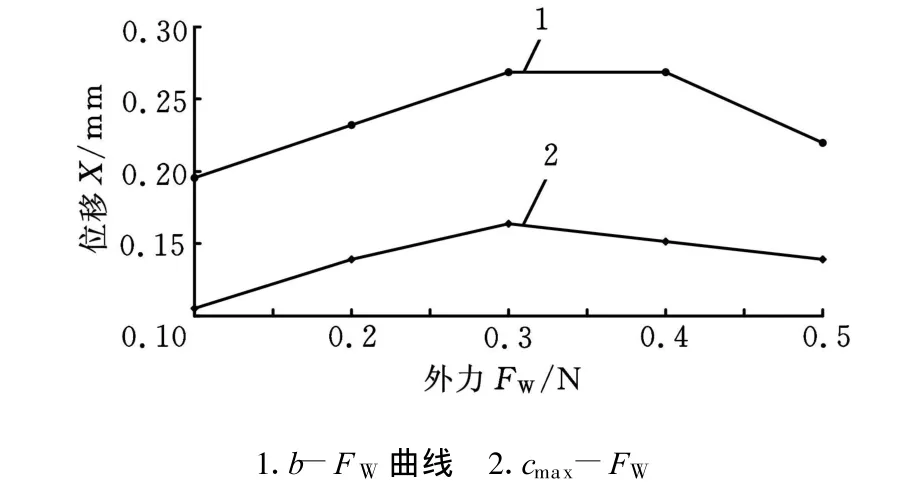
图6 外力-位移曲线
由图 5、图 6、图 7可见,在大气隙(大于5mm)下,电磁力计算公式不再适用(该公式只适用于小气隙的场合)。系统在小外力的情况下振动最好,但不是外力越大越差,而是在中间的某个外力值使系统达到最大的超调量与最大的峰值,此时系统性能最差。系统具有很好的静态性能,在最大承载力范围内能保证稳态准确。
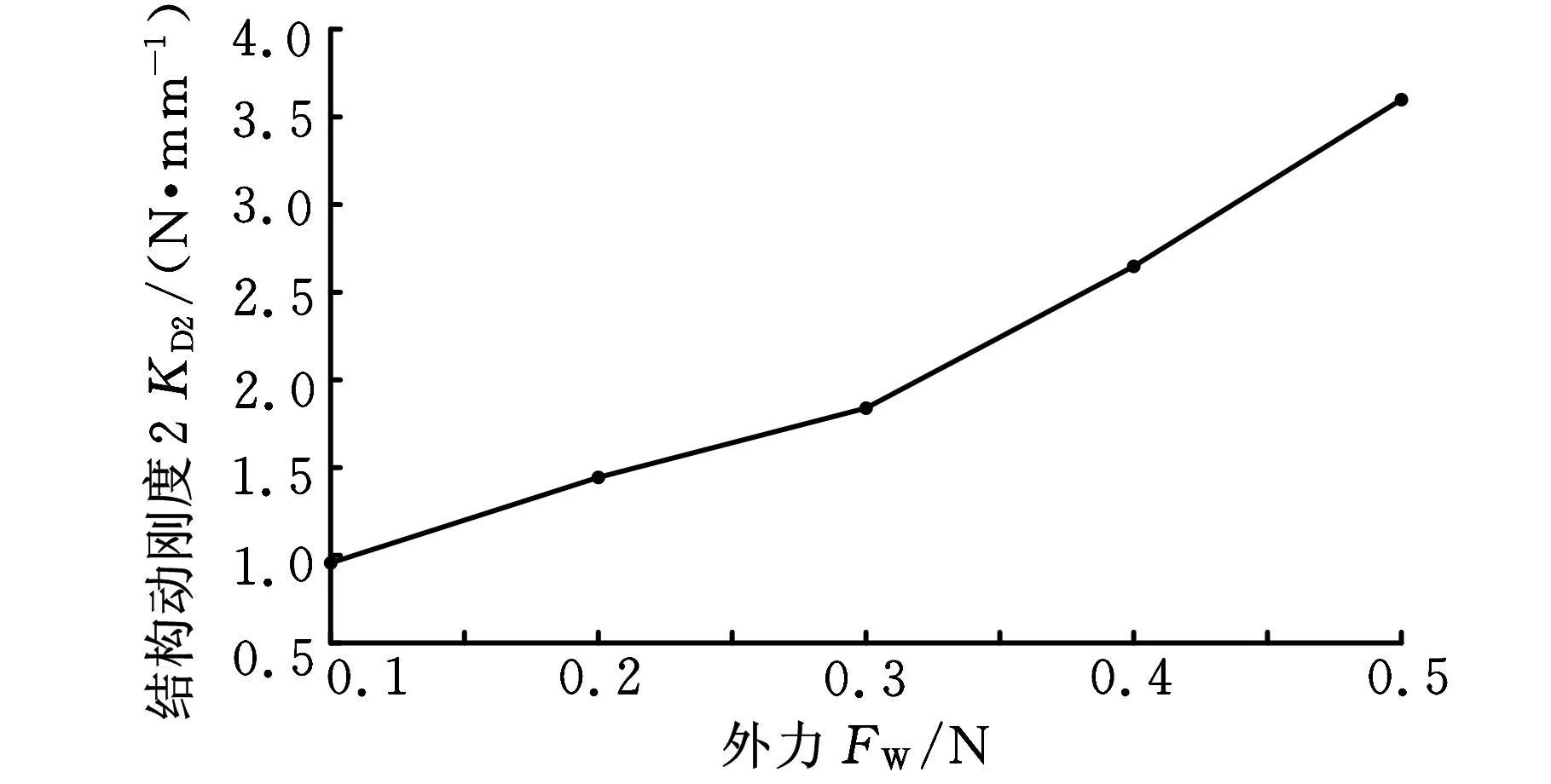
图7 外力-结构动刚度2曲线
4 结构动刚度的测量
用B&K激振器对盘片加载不同正弦信号的激振力。
4.1 加载大小为1N,不同频率的激振力
根据测量数据,计算出 Δx、动刚度1(Δx)、超调量c(mm)、最大超调量c max、最大峰值b(mm)、动刚度2(F W/c max),据此绘制的激振频率-位移曲线、激振频率-三种位移曲线、激振频率-动刚度1曲线、激振频率-动刚度2曲线,分别如图8、图 9、图 10 、图 11 所示。
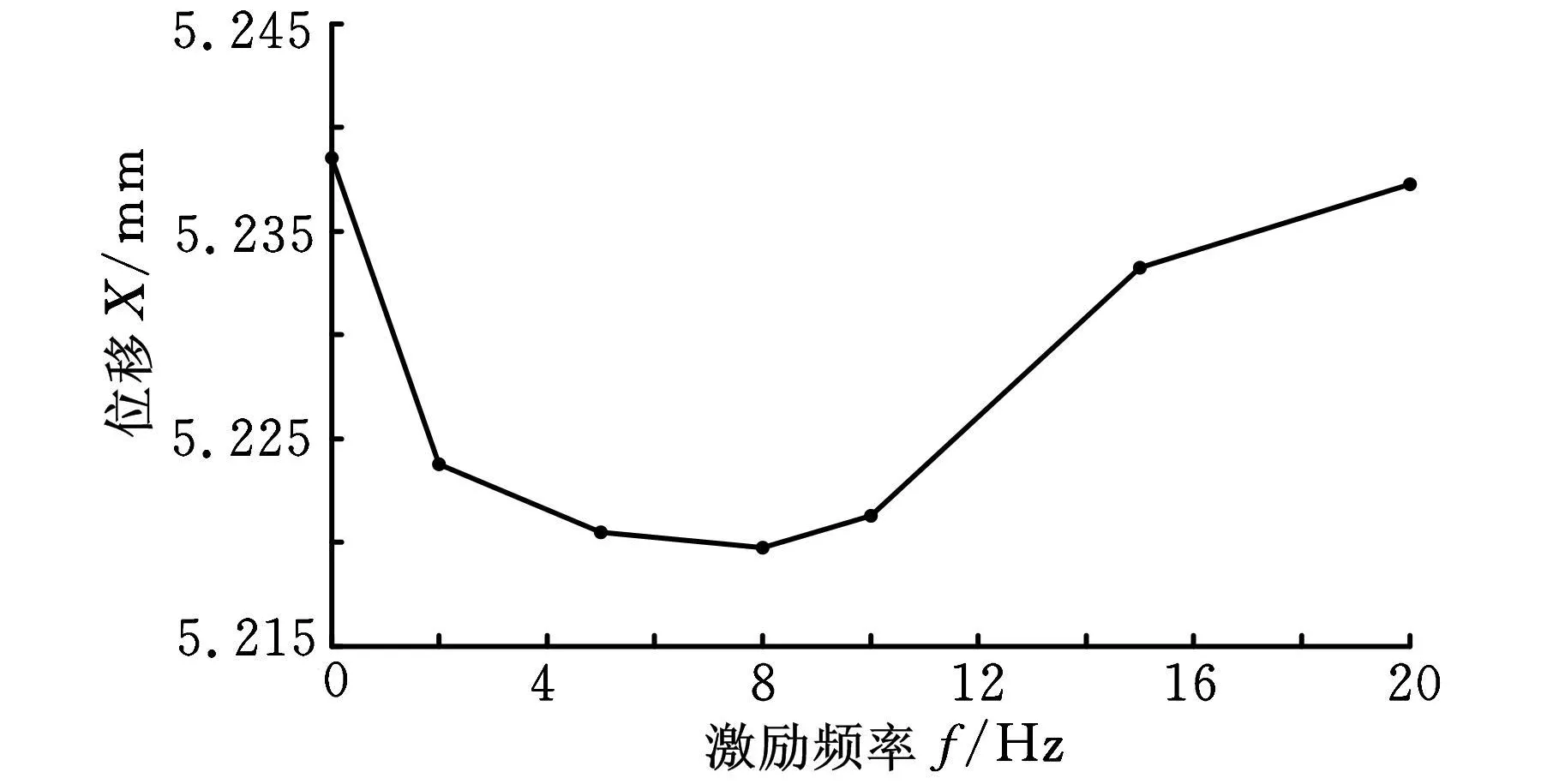
图8 激振频率-位移曲线
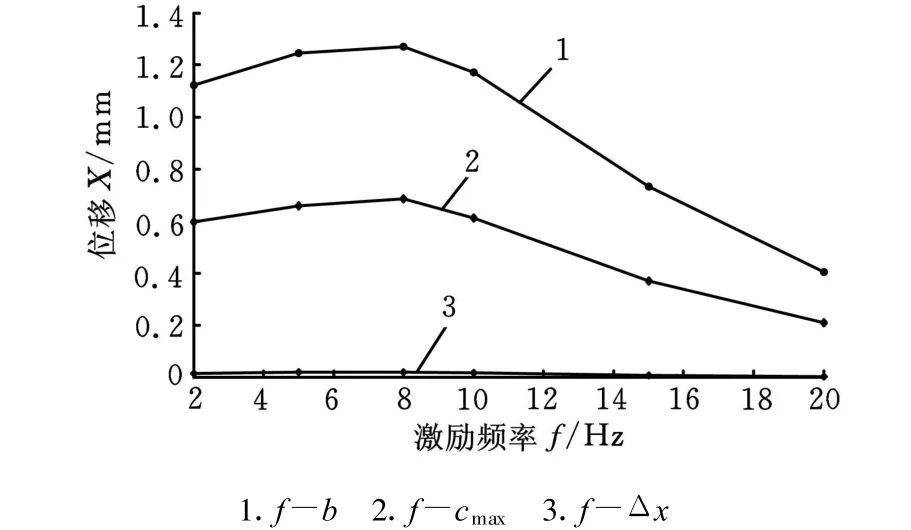
图9 激振频率-三种位移曲线
由图8至图11曲线可见,在8Hz左右系统存在共振频率,这与以前的实验结果相一致[4];在中间频率系统振动比较明显,控制电流最大,电磁力最大,导致平衡位置上移;系统动刚度与外力的频率相关,频率较大和较小时刚度相对增强,尤其是高频部分,中间部分刚度相对而言低些,这与文献[2]研究结论一致;用动刚度1(F W/Δx)与动刚度2(F W/c max)描述磁力系统的结构特性有相同的效果,因此,用两种方式描述结构动刚度都可以;在稳定范围内系统抵抗高频的性能最好,其次是较低频率范围,在共振频率附近最不好。
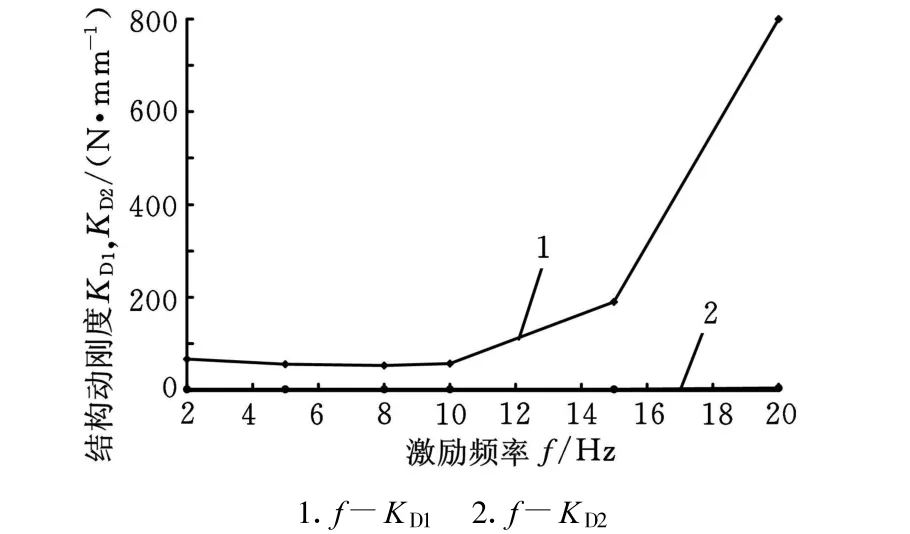
图10 激振频率-动刚度1曲线
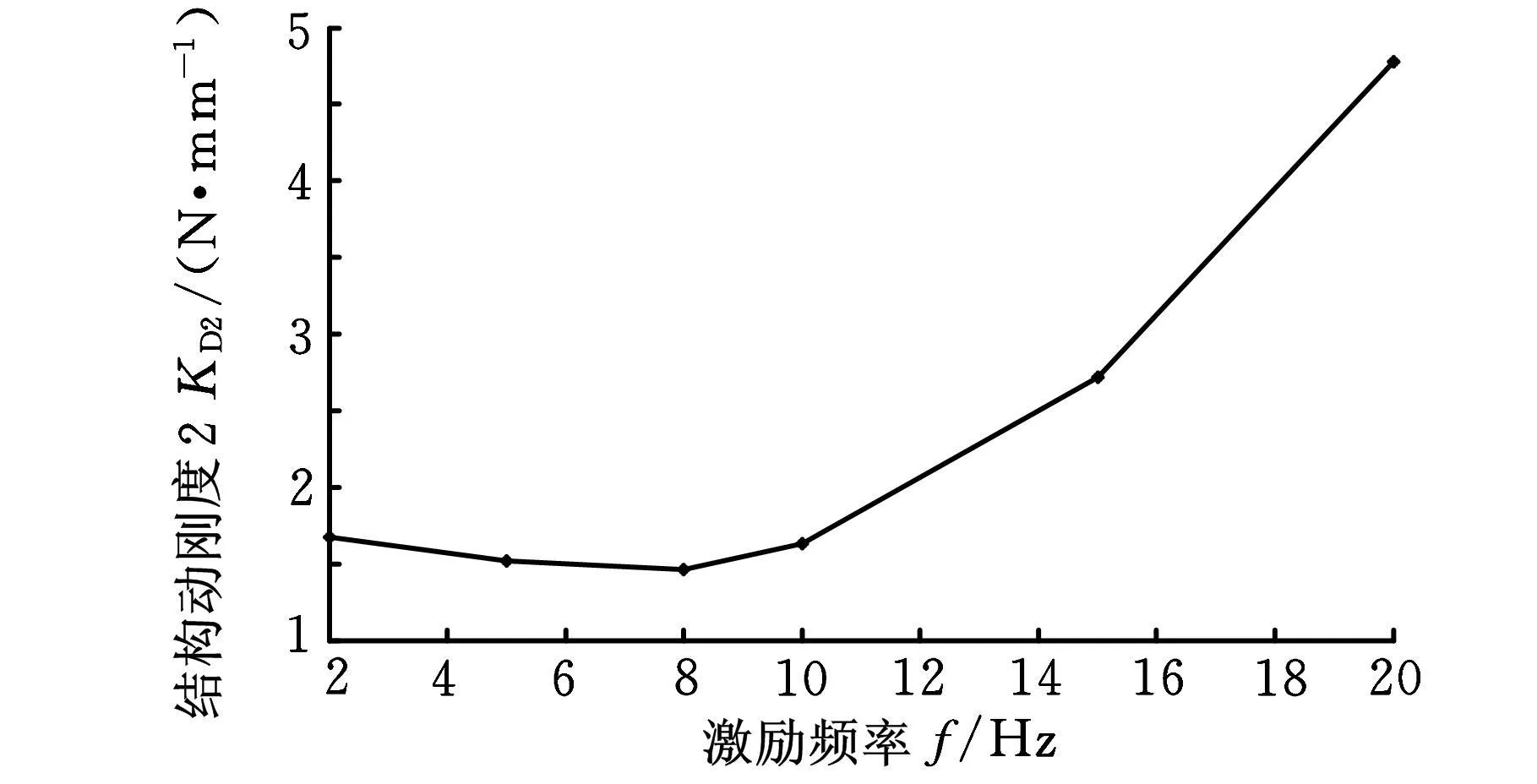
图11 激振频率-动刚度2曲线
4.2 加载频率为10Hz,不同大小的激振力
同样,根据测量数据绘制的外力-位移曲线、外力-三种位移曲线、外力-动刚度曲线、外力-动刚度2曲线,分别如图12、图 13、图14和图 15所示。
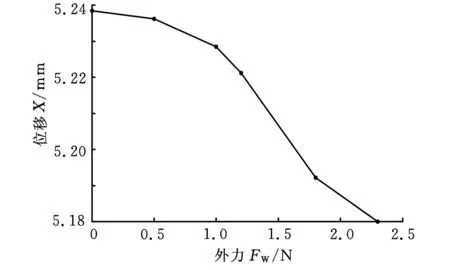
图12 外力-位移曲线
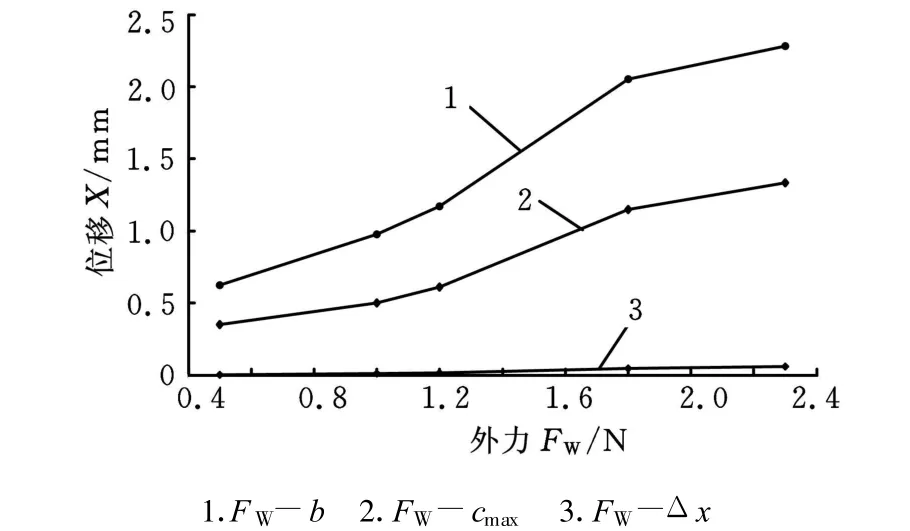
图13 外力-三种位移曲线

图14 外力-动刚度曲线
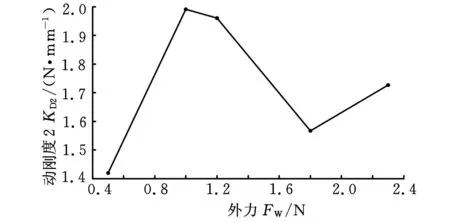
图15 外力-动刚度2曲线
从图12~图15可见,外力在很小范围内对系统影响不明显,如本系统中外力小于1N,但随着外力的增大,系统稳定性变差,振动振幅加大,直至失稳边缘;系统抵抗变形的动刚度随着外力而减小,在最大承载力附近达到最小,超过此值系统失稳;当讨论动刚度与外力频率关系的时候,用动刚度1与动刚度2描述效果一样。但当讨论的是系统动刚度与外力大小关系的时候,用动刚度1与动刚度2描述的效果是不相同的;系统动态承载力远远小于静态承载力。
5 比较两种测量动刚度方案的结果
在此次实验前用另外一种方法对盘片加激振外力,在一路电涡流传感器的输出中设计了附加干扰模块电路,模拟传感器受到的外界干扰[4-5]。通过信号发生器产生幅值可调、频率可调的正弦波,把盘片位移传感器S1的输出信号与信号发生器产生的正弦波叠加输入到控制系统中,改变信号发生器输出的正弦波幅值、频率,直到磁悬浮盘片失稳、跌落为止,通过示波器观察盘片三路位移发生器输出信号的变化,得到图16所示的盘片最大振幅与正弦波频率曲线(选取其中S3)。
(1)0.3V时改变不同频率,用得到的数据绘制的激励频率-最大超调量曲线、激励频率-等效刚度曲线如图 17、图18所示(40Hz盘片失稳),等效刚度K e为电压与最大超调量的比值,即K e=U/c max。
(2)10Hz时不同电压下得到的数据绘制的电压-最大超调量曲线与电压-等效刚度曲线,如图19、图20所示。

图16 频率-最大振幅曲线
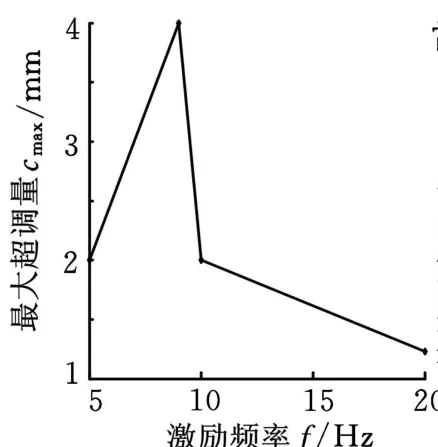
图17 激励频率-最大超调量曲线
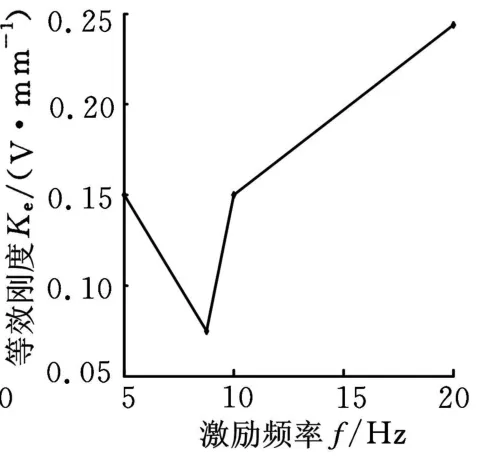
图18 激励频率-等效刚度曲线
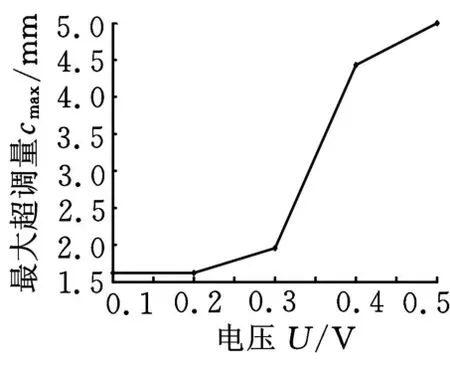
图19 电压-最大超调量曲线
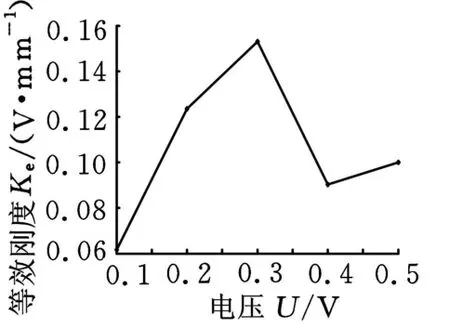
图20 电压-等效刚度曲线
比较图 17与图9,最大超调量趋势基本相同,比较图18与图11,动刚度2基本趋势也相同;比较图19与图13,最大超调量趋势基本相同,比较图20与图15,动刚度2趋势也基本相同,说明本次实验测量正确。
6 结论
(1)磁悬浮系统在外力作用下稳定阶段抵抗高频干扰的能力强,抵抗低频干扰的能力较强,抵抗中间频率干扰的能力较弱;
(2)a、b、c是研究动刚度的3个重要参数,频率 -a、b、c曲线与外力-a、b、c曲线反映磁悬浮系统随外力频率与大小变化时振动的状态;
(3)动刚度1与动刚度2在描述频率与刚度之间关系的时候是相同的,在描述外力大小与刚度之间关系的时候是不相同的;
(4)系统动刚度在外力频率较大和较小时比较好,尤其在相对高频部分刚度好,中间部分刚度低;
(5)动刚度1随外力增大而减小,动刚度2随外力增大先增大再减小再增大。
(6)用直接对对象加激振力的方法与在控制环节对对象加载正弦信号方法测结构动刚度都是可以的。
[1] 赵雷,丛华.可控磁悬浮轴承刚度与阻尼特性研究[J].清华大学学报,1999,39(4):96-99.
[2] 汪希平.电磁轴承系统的刚度阻尼特性分析[J].应用力学学报,1997,14(3):95-101.
[3] 胡业发,周祖德,江征风.磁力轴承的基础理论与应用[M].北京:机械工业出版社,2006.
[4] 张薇薇.基础运动对磁悬浮转子系统动力学特性的影响研究[D].武汉:武汉理工大学,2009.
[5] 冯斌.磁悬浮转子状态监测与故障诊断[D].武汉:武汉理工大学,2009.

