未知传递函数情况下主动电磁悬浮系统支承特性在线测量

蒋科坚 祝长生

浙江大学,杭州,310027

0 引言

以主动电磁轴承为代表的电磁悬浮系统,其魅力不仅在于它是一种无摩擦的支承装置,更重要的是其动力特性可通过控制策略进行在线调节优化。前者决定了主动电磁悬浮能够应用在高速场合;后者使得可以通过控制策略的设计,优化主动电磁悬浮在不同频段的支承特性,调节支承刚度和阻尼,实现对振动的主动控制。

主动电磁悬浮系统的支承特性研究大多是以等效刚度和等效阻尼为基础展开的。但是,电磁悬浮系统支承的等效刚度和阻尼不仅与结构尺寸有关,而且还受到其控制器所采用的控制策略的影响。只有在已知控制系统传递函数的前提下,才可能对支承的等效刚度和阻尼进行理论计算。但是,目前在电磁悬浮系统中各种新型的智能控制策略都得到了成功的应用,这些控制策略大都无法归结出相应的传递函数,造成无法通过理论计算获知系统支承的等效刚度和阻尼,从而难以深入地研究主动电磁悬浮系统的动力特性。因此,在未知系统传递函数的情况下,如何确定支承的等效刚度和阻尼是主动电磁悬浮系统动力学研究中必须解决的一个关键问题。

早在1980年,Haberman[1]就对电磁轴承的刚度作了研究,并提出了“浴盆”形复刚度曲线。此后,多数研究者均以此为基础分析主动电磁轴承系统的动力特性。Humphris等[2]以主动电磁轴承系统的传递函数推导出了电磁轴承的等效刚度和阻尼的计算公式。在国内,汪希平[3]、曹洁[4]较早地对主动电磁轴承的等效刚度和阻尼特性进行了理论分析。赵雷等[5]分析了控制环节各参数对主动电磁轴承的刚度特性的影响。胡业发等[6]基于电磁力分析了电磁轴承的刚度和阻尼特性。吴华春等[7]就滤波、滞后、衰减等因素对电磁轴承刚度的影响进行了分析。杨作兴等[8]提出了对主动电磁轴承复刚度的测试方法,但没有涉及在电磁轴承转子动力学研究中使用更多的等效刚度和阻尼的测试。目前文献对等效刚度和阻尼的分析研究大多是在已知传递函数的前提下进行的。

本文首先分析了主动电磁悬浮系统支承的等效刚度和阻尼的理论计算方法,然后提出一种不依赖系统传递函数的等效刚度和阻尼的在线测试方法,并进行了实验,取得了与理论分析十分相近的结果。

1 等效刚度和等效阻尼的理论表达式

主动电磁悬浮系统不管是采用什么样的控制策略,最终表现出来的支承特性可以用支承的刚度和阻尼来表示。对于一个单自由度的质量-弹簧-阻尼系统,系统的运动方程为

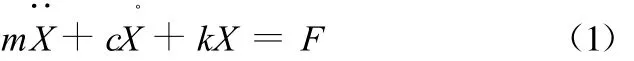
式中,F为物体所受到的外激励力;m为质量;k、c分别为系统的刚度和阻尼系数。

将式(1)进行拉普拉斯变换,可得其频率特性方程为

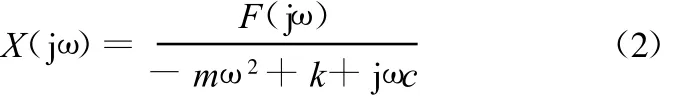
同样考虑一个单自由度的主动电磁悬浮系统,如果不考虑其他外阻尼的影响,在线性条件下其运动方程为

式中,fAMB为主动电磁悬浮系统产生的电磁力;kx、ki分别为系统的位移刚度和电流刚度系数;i为控制电流。

如果将控制电流与悬浮位移之间的关系表示为传递函数的形式,即 I(s)=G(s)X(s)。G(s)为主动电磁悬浮控制系统整体的传递函数,一般是位移传感器、输入AD、控制器算法、输出DA、功率放大器等各个控制环节传递函数的总和。将此式代入式(3)并经拉普拉斯变换,其频率特性方程形式为

比较式(2)、式(4),容易得出电磁悬浮系统相对于质量-弹簧-阻尼系统的等效刚度K e和等效阻尼C e的表达式：

式中,Re(G(jω))、Im(G(jω))分别为控制系统传递函数G(s)的实部和虚部。

显然,如果已知控制系统传递函数G(s)的表达式,那么就能够容易地对主动电磁悬浮系统的等效刚度K e和阻尼C e进行理论计算。但事实上由于许多控制系统无法归结出一个传递函数表达式,因此就难以对其等效刚度和阻尼特性进行理论分析。为此,本文提出一种不依赖系统传递函数的等效刚度和阻尼的在线测定方法。

2 等效刚度和等效阻尼在线测量

图1所示为无外阻尼的单自由度主动电磁悬浮控制结构图。F(t)为外激励力,X(t)为转子相应的位移响应。为讨论方便,设参考信号R=0。根据模型等效原则,图1可简化为图2所示的等效结构。

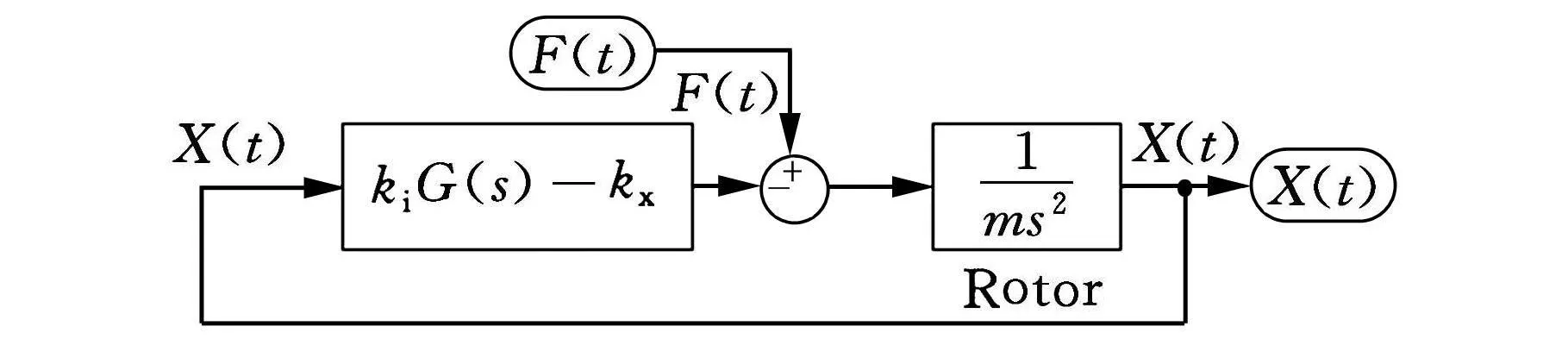
图2 电磁悬浮控制结构简化

由式(4)、式(5)可知,求解电磁悬浮系统的等效刚度和阻尼值,实质上就是求解图2中k i G(s)-k x部分的传递函数特性。系统的等效刚度就等于kiG(s)-kx的实部,其虚部除以ω就是等效阻尼。很自然,最直观的想法是通过测试G(s)的传递函数特性,从而换算得到系统的等效刚度和阻尼。虽然这样的想法在理论和仿真中是可行的,但由于需要控制系统脱离电磁悬浮系统单独进行测试,实际测试难度较大。

从图2可知,外激励力与位移响应之比具有刚度的量纲,被称为复刚度或动刚度,用K v表示为

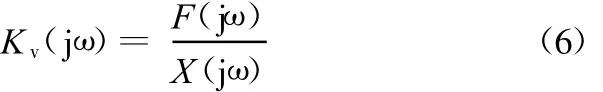
复刚度K v通常用复数形式或幅值相角形式表示,描述在不同频率下,外激励力与位移响应在复平面上的幅值关系和相位关系。|K v|随频率变化的关系就是前面讲到的“浴盆”曲线。由式(6)可知,复刚度实质上是从外力到位移响应闭环频率特性的倒数。闭环频率特性可以通过实验直接测得,文献[3,8]就是基于这样的原理提出实验测量复刚度的方法。与复刚度含义不同,等效刚度和等效阻尼是将电磁悬浮支承等效成传统的质量-弹簧-阻尼系统后所对应的刚度的阻尼值。复刚度和等效刚度及阻尼都是描述系统刚度特性的量,只是描述的角度不同,因此应用领域也不同。在电磁轴承转子动力学研究中通常用等效刚度和等效阻尼描述轴承的支承特性。

在控制系统的分析中,常见情况是知道系统的开环频率特性,来求解系统闭环后的频率特性。本文的思路正好相反,试图通过先对 F(s)和X(s)进行闭环频域测试,然后反向推算其中k i G(s)-k x部分的开环特性,得到系统的等效刚度和等效阻尼。

首先,分析F(s)到X(s)闭环频率特性和等效刚度阻尼的关系,整理式(4)和式(6)得

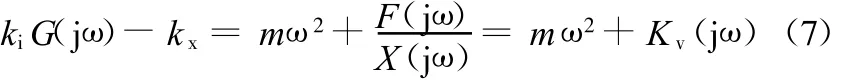
根据式(7),可求得kiG(s)-kx的开环频域特性。由于从外力到位移响应闭环频率特性的倒数就是复刚度。因此,复刚度的实部中加上 mω2即为kiG(s)-kx的实部,就是主动电磁悬浮系统在ω频率下的等效刚度值;复刚度的虚部除以 ω就是等效阻尼。在不同ω的外激振下,可以得到一组闭环频率特性值,进而计算出一系列不同频率下的等效刚度和阻尼值。

理论上讲,当线性系统输入正弦激振信号时,其输出也为正弦。但在实际系统中,由于被测系统的非线性和随机干扰,其输出信号不可避免地混杂有其他频率的杂波干扰。如何从输出信号中提取相应的输入响应是测量等效刚度和阻尼的关键。设在输入信号U r(t)=U sinω0t的作用下,系统的输出信号Uc(t)为

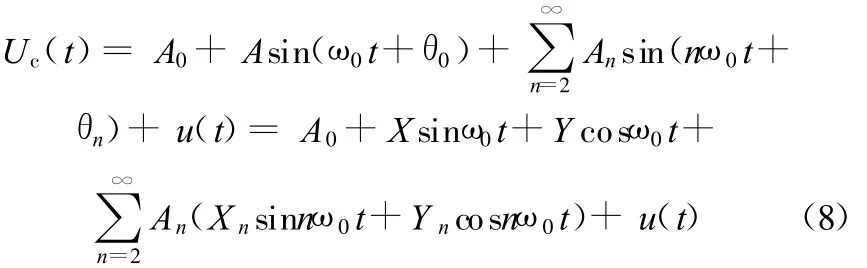
式中,A0为被检信号中直流分量;A sin(ω0t+θ0)为基波分量;u(t)为噪声分量;Ansin(nω0t+θn)为各阶高次谐波分量。

式(8)中,只有基波成分是激振响应成分。为了从这些混杂信号中提取我们所需要的频率成分,采用了信号解调的原理。首先在输出信号U c(t)上分别乘以一个与Ur(t)频率相同的单位幅值的正弦和余弦信号sinω0 t、cosω0t,然后在基波整倍数周期内积分并求平均值：

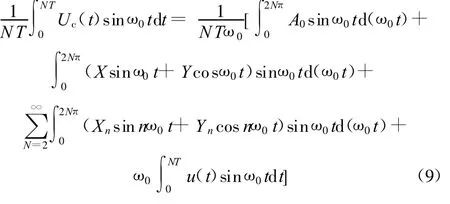
由于正弦函数的正交性和相关性原理,故当N值取较大时,式(9)可以写为

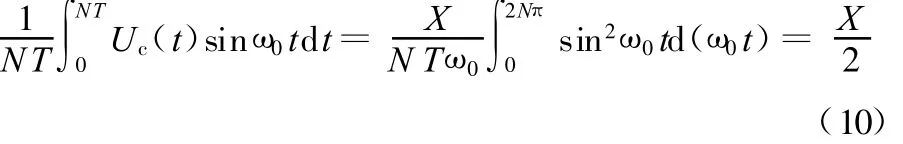
把式(10)中的X表示为ω的函数形式：

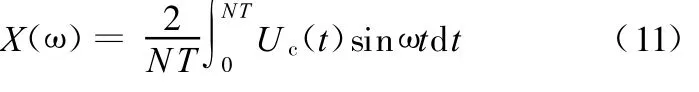
同样地

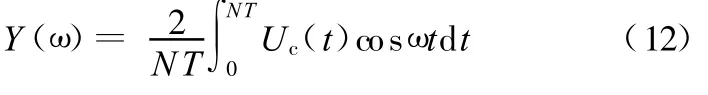
这样,就可以从被测信号中提取出基波分量。在实际应用中,为了增强抗干扰性能,一般取N ＞5。

为了测试电磁悬浮系统的等效刚度和阻尼,必须对系统施加一定的外激振力。施加激振一般有两种途径。其一,采用专门的激振设备,此方法可以完全把被测系统作为“黑箱”处理,即在无需知道被测系统任何参数的情况下测得系统的刚度和阻尼,该方法甚至适用于电磁悬浮系统以外的刚度和阻尼测试对象。但对于电磁悬浮系统,必须采用非接触式的激振力,否则激振器会对主动电磁悬浮系统动力特性产生明显影响。因此,可以利用电磁悬浮系统本身的特点,通过在励磁线圈中叠加正弦电流,从而产生正弦激振力。此方法简单,不附加额外设备,对被测对象的附加影响小,但需要知道电磁线圈的电流系数k i才能完成电流到激振力的换算。

3 PID控制的等效刚度和阻尼的理论计算

为了对比实验结果与理论计算结果,选择标准的PID控制器作为算例,分析控制参数对电磁悬浮支承特性的影响。控制器传递函数为K p+K i/s+K d s,其中 K p、K i、K d 分别为控制器中的PID参数。设功率放大器倍数为Kw,位移传感器转换倍率为K c,系统的整体滞后时间常数为T,则整个控制系统的传递函数G(s)可表示为

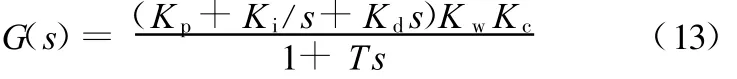
根据式(5),PID控制系统的等效刚度和阻尼表达式为

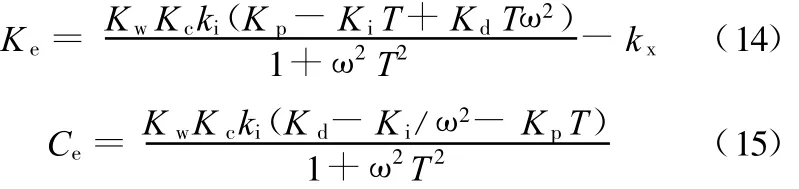
将本文的实验数据代入式(14)、式(15),K w=1A/V,K c=7083V/m,k i=100 N/A,k x=0.2MN/m,T=0.4ms,频率为 1～ 1000Hz。PID控制器K p、K i、K d参数对主动电磁悬浮等效刚度和阻尼影响的计算结果如图3～图8所示。

从图3可知,在100Hz以下的频率较低区域,主动电磁悬浮等效刚度随比例参数Kp值改变的变化较大,而随频率的变化基本不变。对照式(14),由于系统惯性滞后时间T非常小(10-4数量级),在低频区K i T项和K d Tω2项都很小,1+ω2T2项可近似等于1。因此在频率较低时,Kp项成为等效刚度的主要决定因素。随着频率逐渐增大,K d Tω2项的作用渐渐增大,使等效刚度随频率ω逐渐增大。K p值在PID控制中对等效阻尼的影响如图4所示,对照式(15),由于系统惯性滞后时间T非常小,使得K p变化对等效阻尼在整个频率区域的影响都很小。在100Hz以下的低频区域,等效阻尼基本保持恒值。随着频率逐渐增大,分母项1+ω2T2随之增大,导致等效阻尼在高频区域逐渐减小。

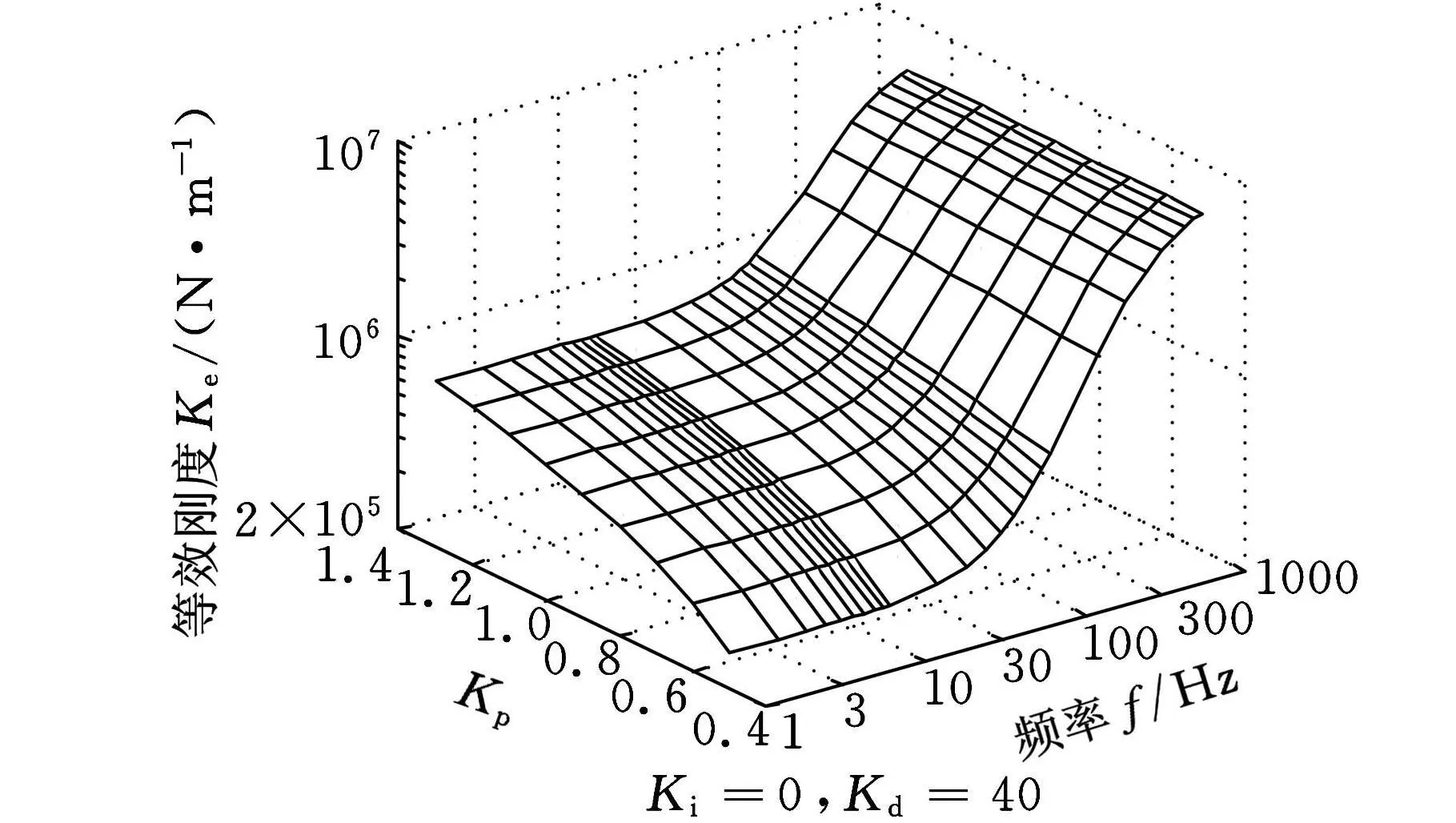
图3 K p值在PID控制中对等效刚度的影响

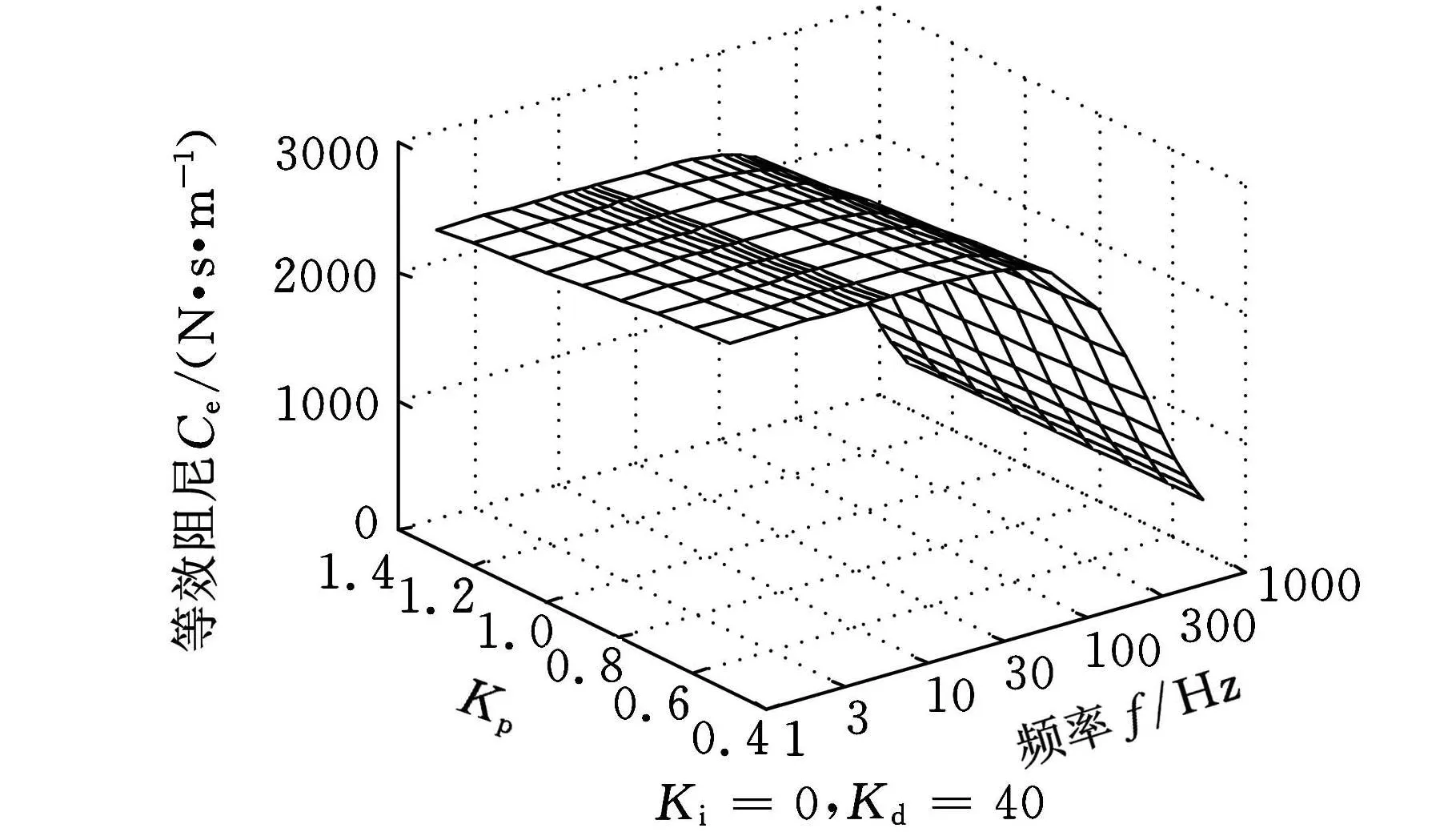
图4 K p值在PID控制中对等效阻尼的影响

从图5可知,在100Hz以下的低频区域,微分参数K d对等效刚度无明显影响。在高频区域,由于K d Tω2项的作用,K d对等效刚度影响逐渐增大。如图6中的Kd对等效阻尼有明显的影响,在整个频率范围内,等效阻尼都起决定作用。在频率较高时,由于分母项1+ω2T2的影响,K d对等效阻尼的影响稍稍减弱。

从图7所示可知,积分参数K i对等效刚度几乎无影响。图8显示,K i会使得等效阻尼在低频区域大幅减小。Ki=0时,低频区的等效阻尼基本保持恒值。K i越大,等效阻尼在低频区的减小幅度也越大。

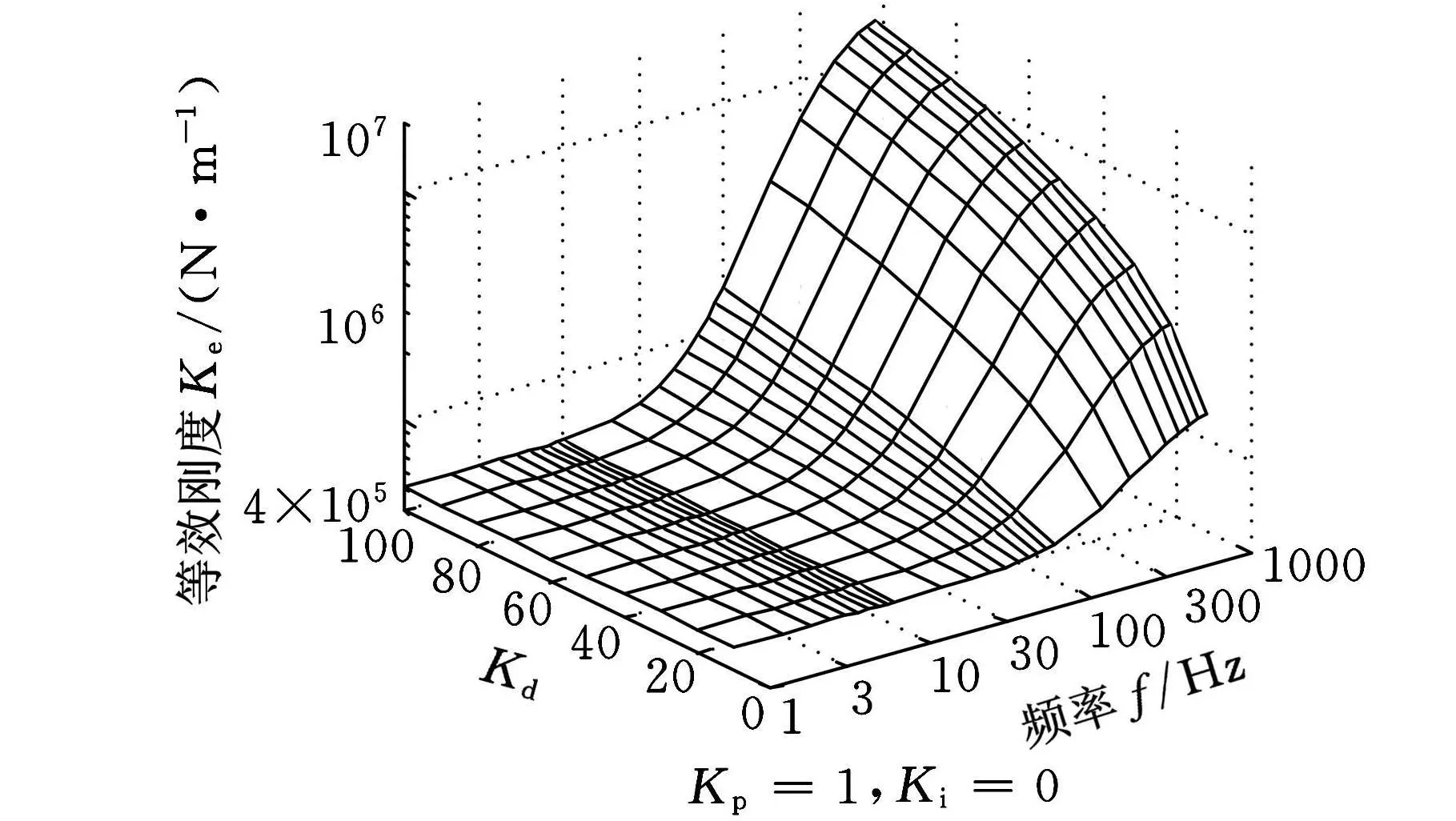
图5 K d值在PID控制中对等效刚度的影响

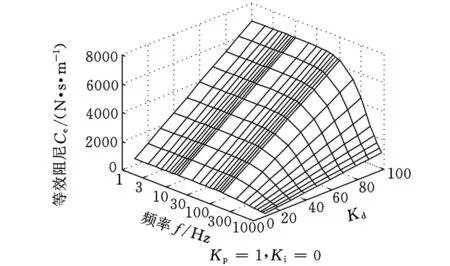
图6 K d值在PID控制中对等效阻尼的影响

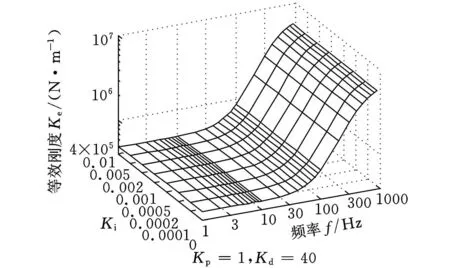
图7 K i值在PID控制中对等效刚度的影响

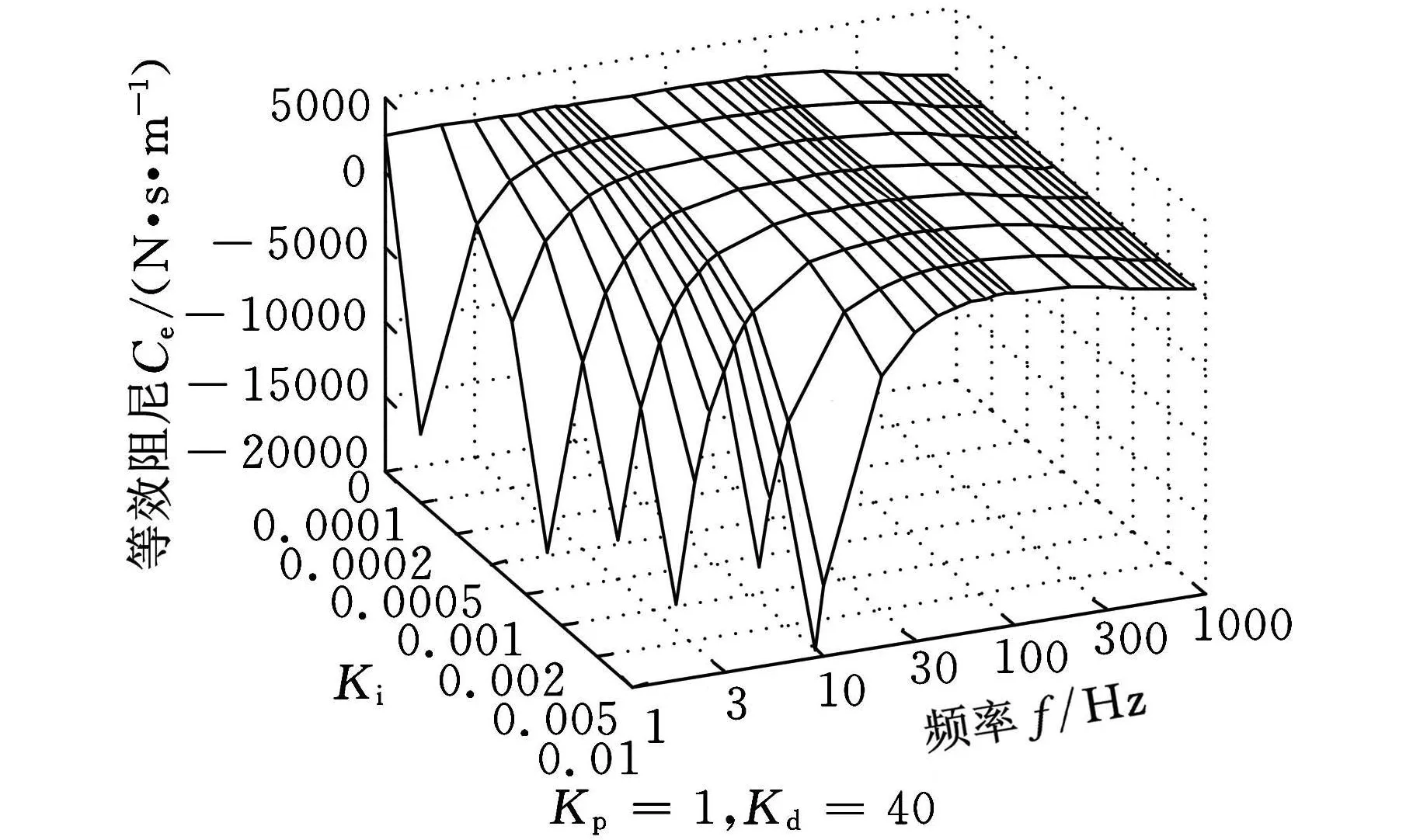
图8 K i值在PID控制中对等效阻尼的影响

4 刚度阻尼的在线识别实验

4.1 实验装置

实验在图9a所示的杠杆式单自由度主动电磁悬浮实验台上进行。杠杆的一端与铰链相连,另一端由主动电磁悬浮支承。由于铰链支承和杠杆的刚度远远大于电磁悬浮系统所提供的刚度,所以可以将杠杆机构等效成图9b所示的质量-弹簧-阻尼系统,系统的等效质量为M=(l/a)2m。实验采用标准的离散PID控制,采样频率为10k Hz,测试频率范围为1～1000Hz。

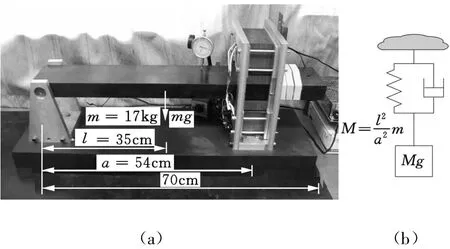
图9 杠杆式单自由度主动电磁悬浮系统实验台

4.2 PID参数对刚度和阻尼影响的实验

图10 ～图15所示是在激励力的振幅为18.75N,Kp分别选取 0.8、1.0、1.2,Ki分别选取0、0.0005、0.0010 、0.0050、0.0100,K d 分别选取20、40、60的条件下,在线识别出的主动电磁悬浮系统的等效刚度和等效阻尼随频率的变化曲线。

把图10～图15分别与图3～图8对应比较,可以得到如下结论：

(1)对于等效刚度,实验结果与理论结果在低频区和中频区颇为一致,数值非常接近。但频率超过500Hz后,实验数据与理论计算值的误差逐渐增大,在图12中导致微分参数K d在高频区域对等效刚度的影响不明显。

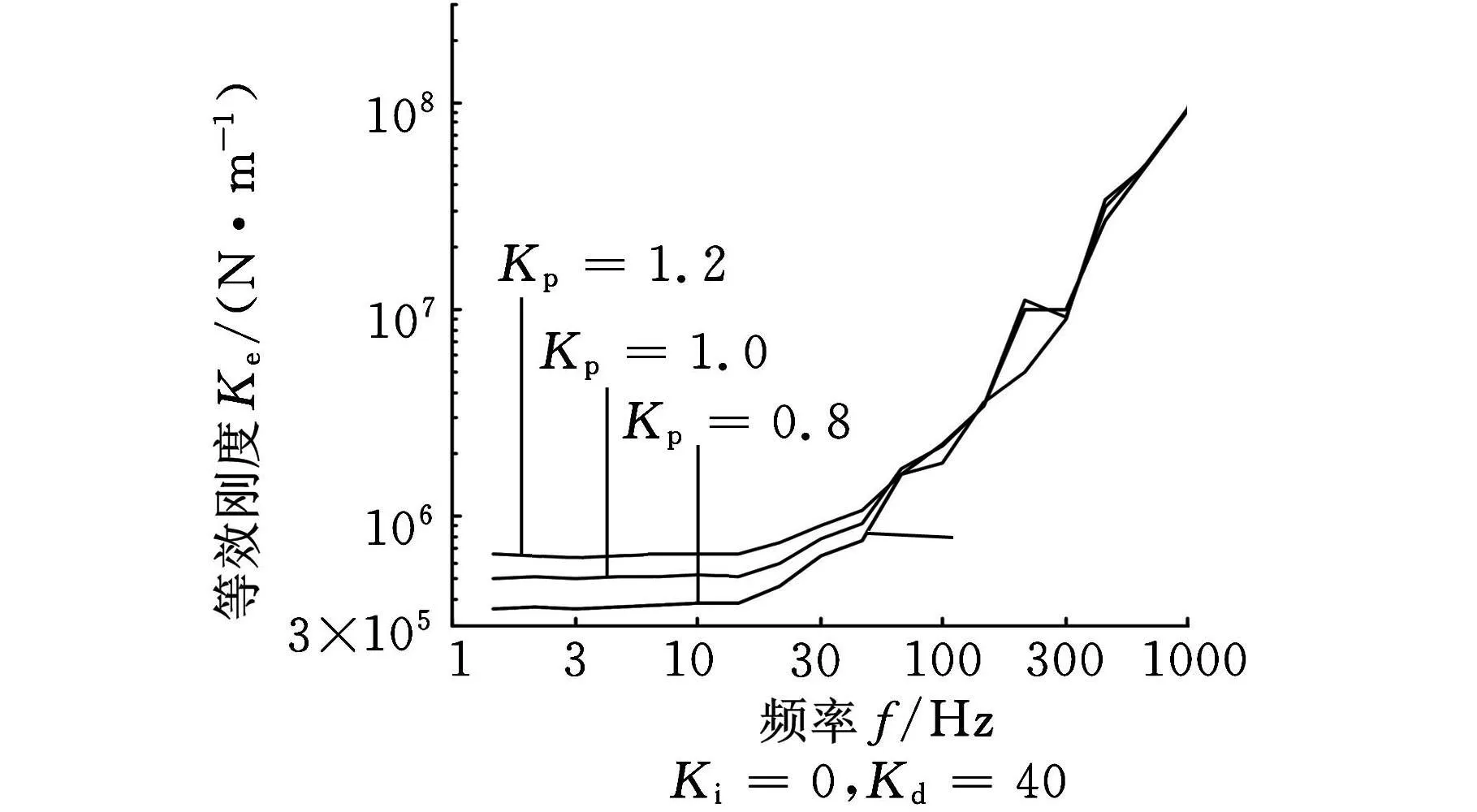
图10 K p值在PID控制中对等效刚度实际影响测试

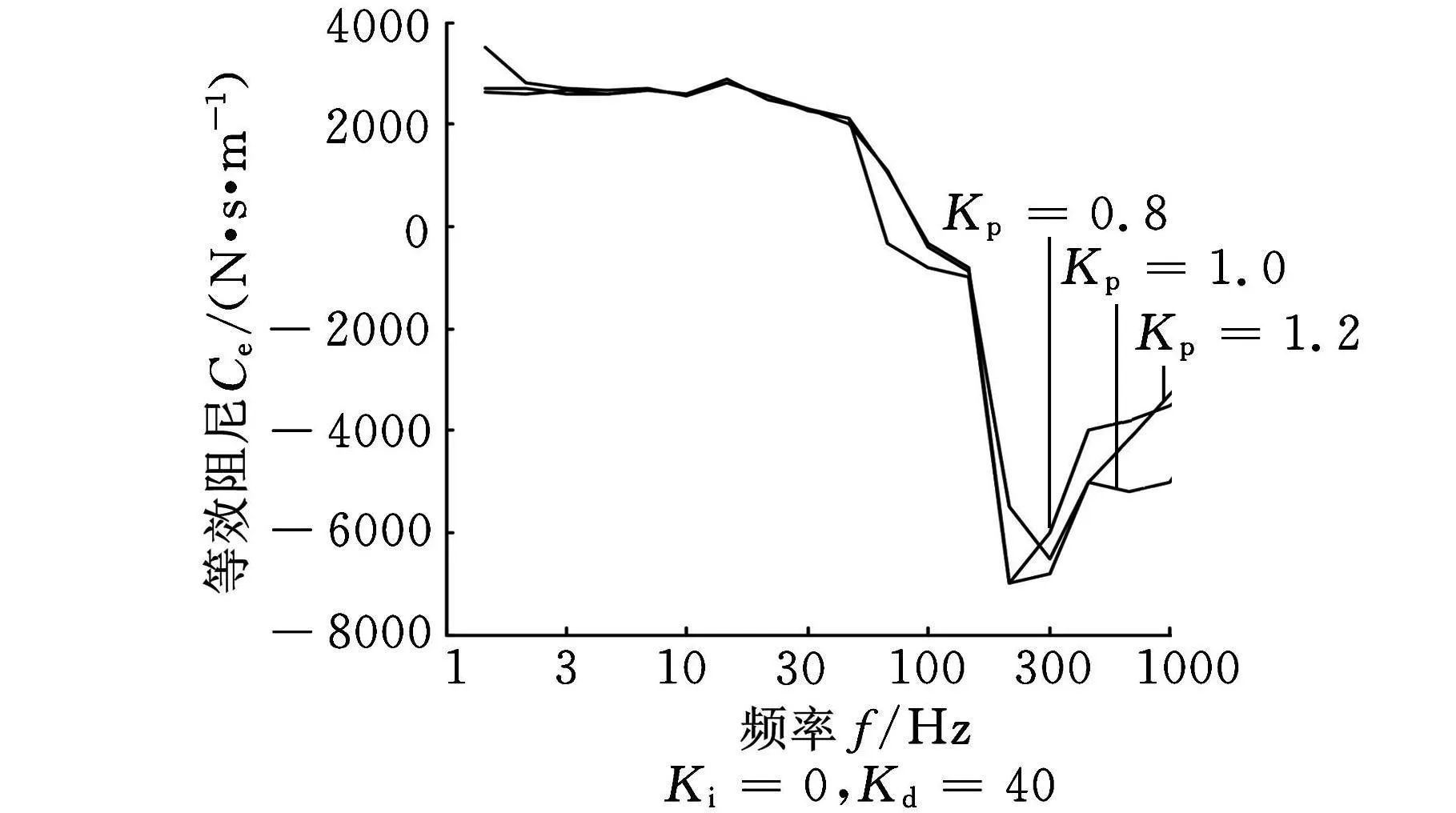
图11 K p值在PID控制中对等效阻尼实际影响测试

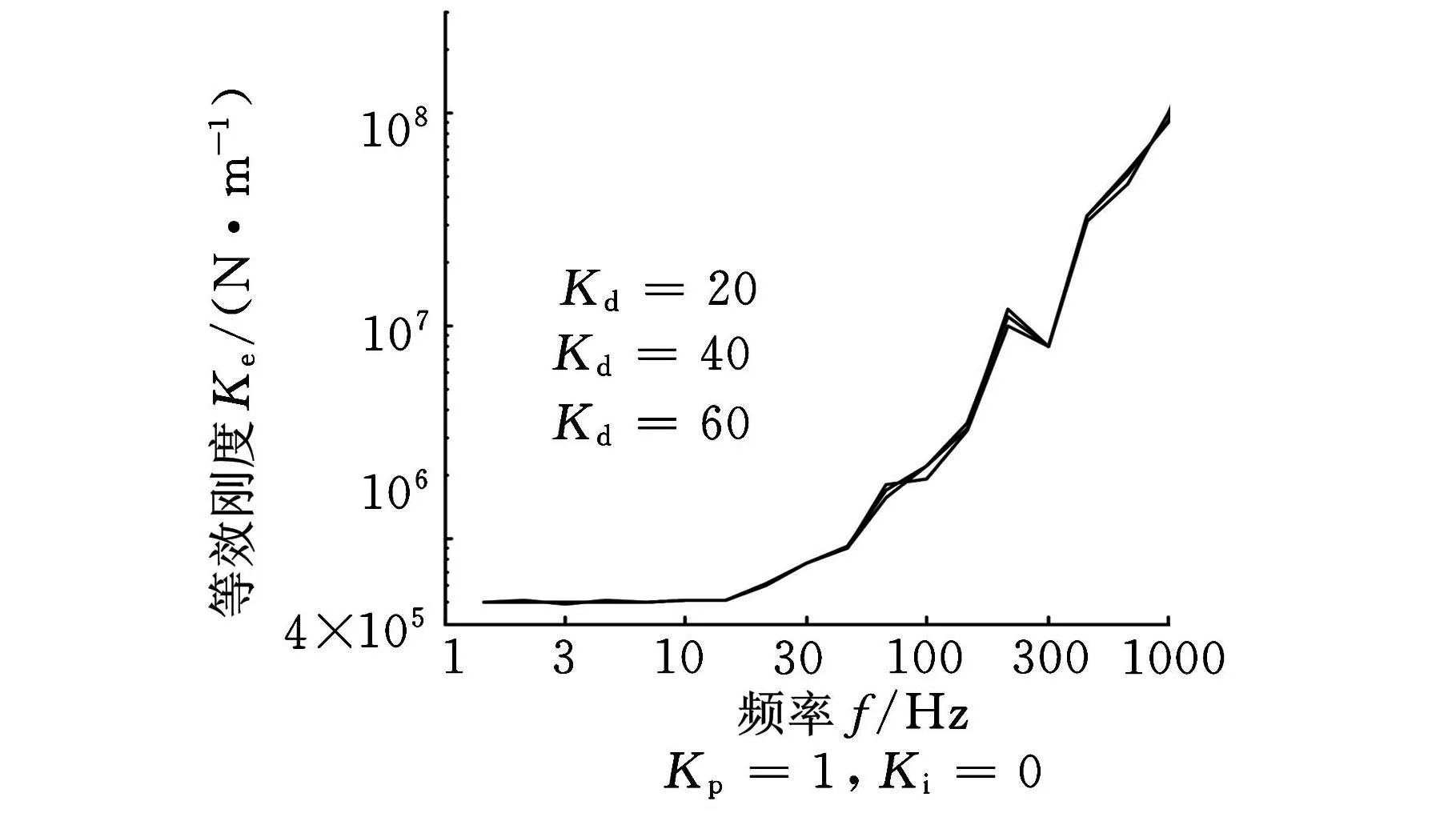
图12 K d值在PID控制中对等效刚度实际影响测试

图13 K d值在PID控制中对等效阻尼实际影响测试

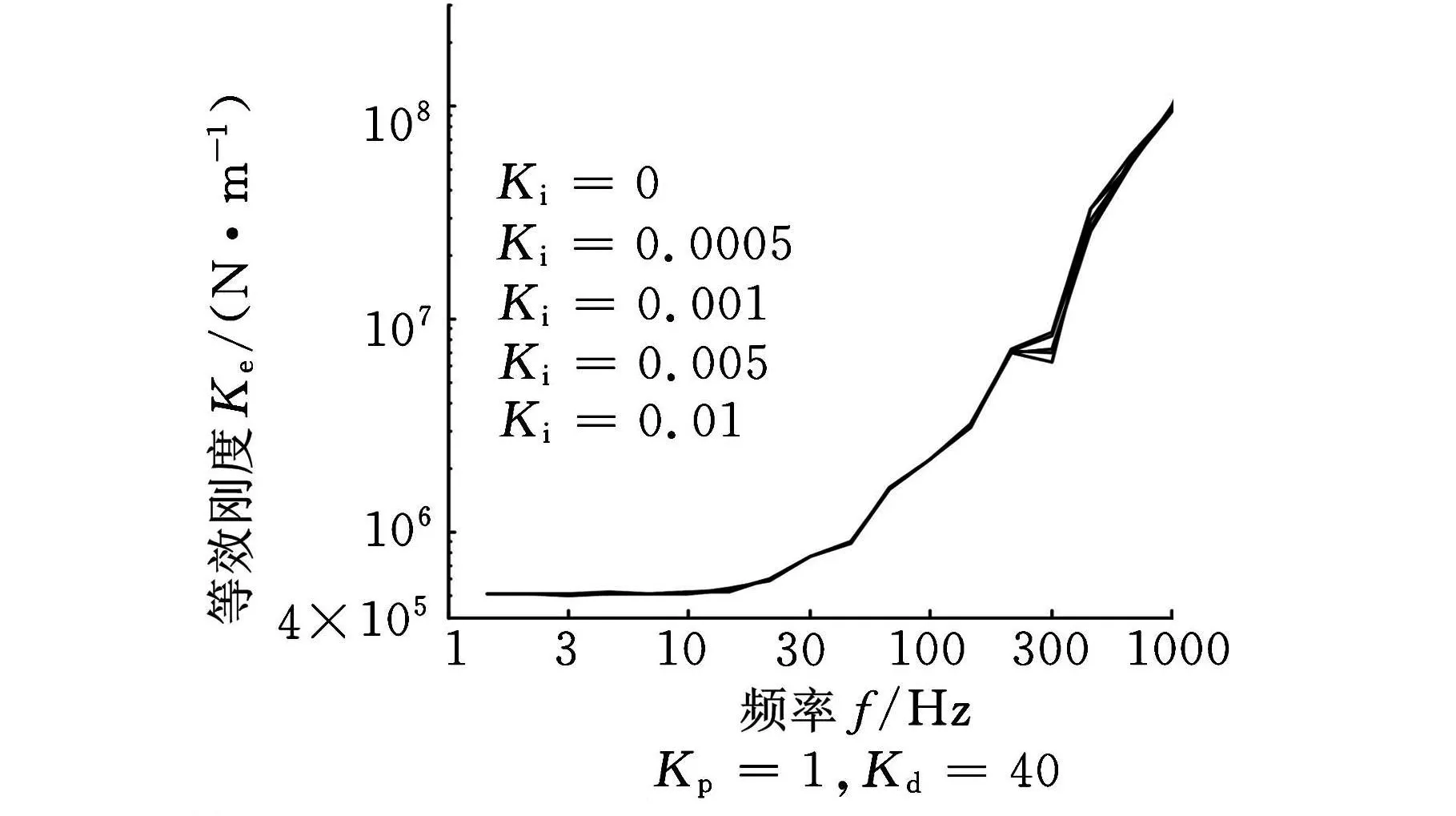
图14 K i值在PID控制中对等效刚度实际影响测试

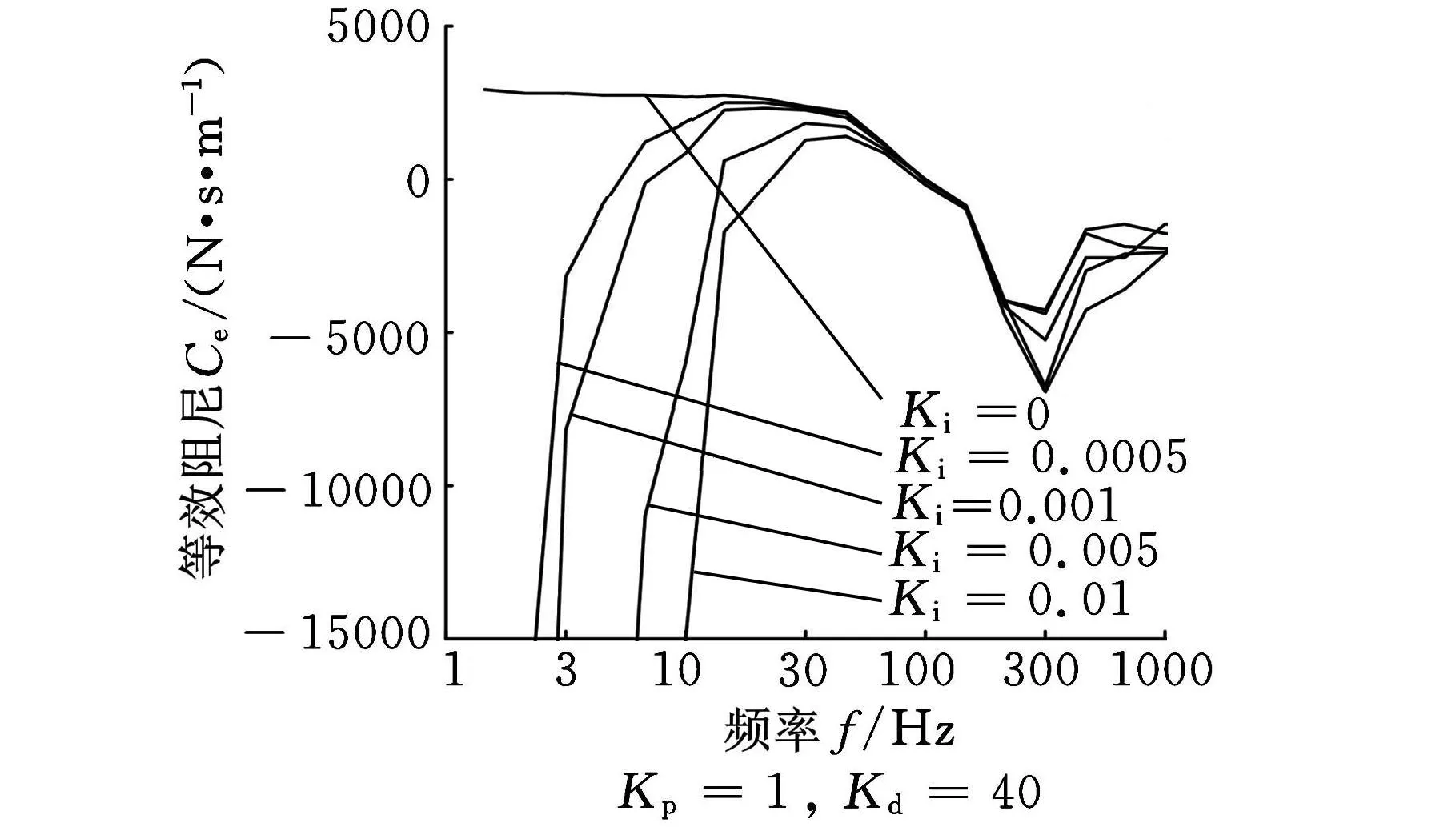
图15 K i值在PID控制中对等效阻尼实际影响测试

(2)对于等效阻尼,同样在低频区和中频区实验识别结果与理论结果有很好的一致性。随着频率升高,两种结果的等效阻尼都在100Hz后开始逐渐减小。但实验识别出的等效阻尼值减小比理论计算值下降得更快,并且在300Hz左右又触底反弹,形成一个V形谷底。谷底反弹后,在600Hz后又与理论计算值基本一致。为了分析形成谷底的原因,我们计算了实验悬浮结构的固有频率。悬浮杠杆结构的固有频率ω0=264.6Hz,这个值与实验测得的谷底频率基本一致。实验中出现V形谷底的原因,是由于在固有频率点引起了系统的共振,加剧了振动的幅度,导致等效刚度K e和等效阻尼C e的识别值减小。从图10～图15中可以观察到,无论是等效刚度还是等效阻尼,在固有频率点都出现了V形拐点,并且随着PID参数的不同,形成的谷底深度也不同。

4.3 激励振幅对测试效果的影响

如果是一个理想的线性系统,激振力的大小不会对等效刚度及阻尼的识别结果产生影响。但是,实际系统往往具有非线性,对于本实验而言,振幅选择过小,同频的位移振动难以检出,识别出的刚度和阻尼的误差较大。振幅选择过大,会影响到主动电磁悬浮的电流线性化和位移线性化条件,同样会造成误差。为了测试不同大小的激振力对等效刚度和阻尼识别效果的影响,实验分别在6.25N、12.50N、18.75N、25.00N、31.25N、37.50N 6种激励力振幅下进行了相关的测试。

在不同激励力下,1～1000Hz频率范围的等效刚度和阻尼变化测试结果如图16、图17所示。在中低频区域,激振力大小对等效刚度和阻尼的识别结果基本没有影响。值得注意的是,在系统的固有频率点,激振力越大,形成的V形谷底越深。

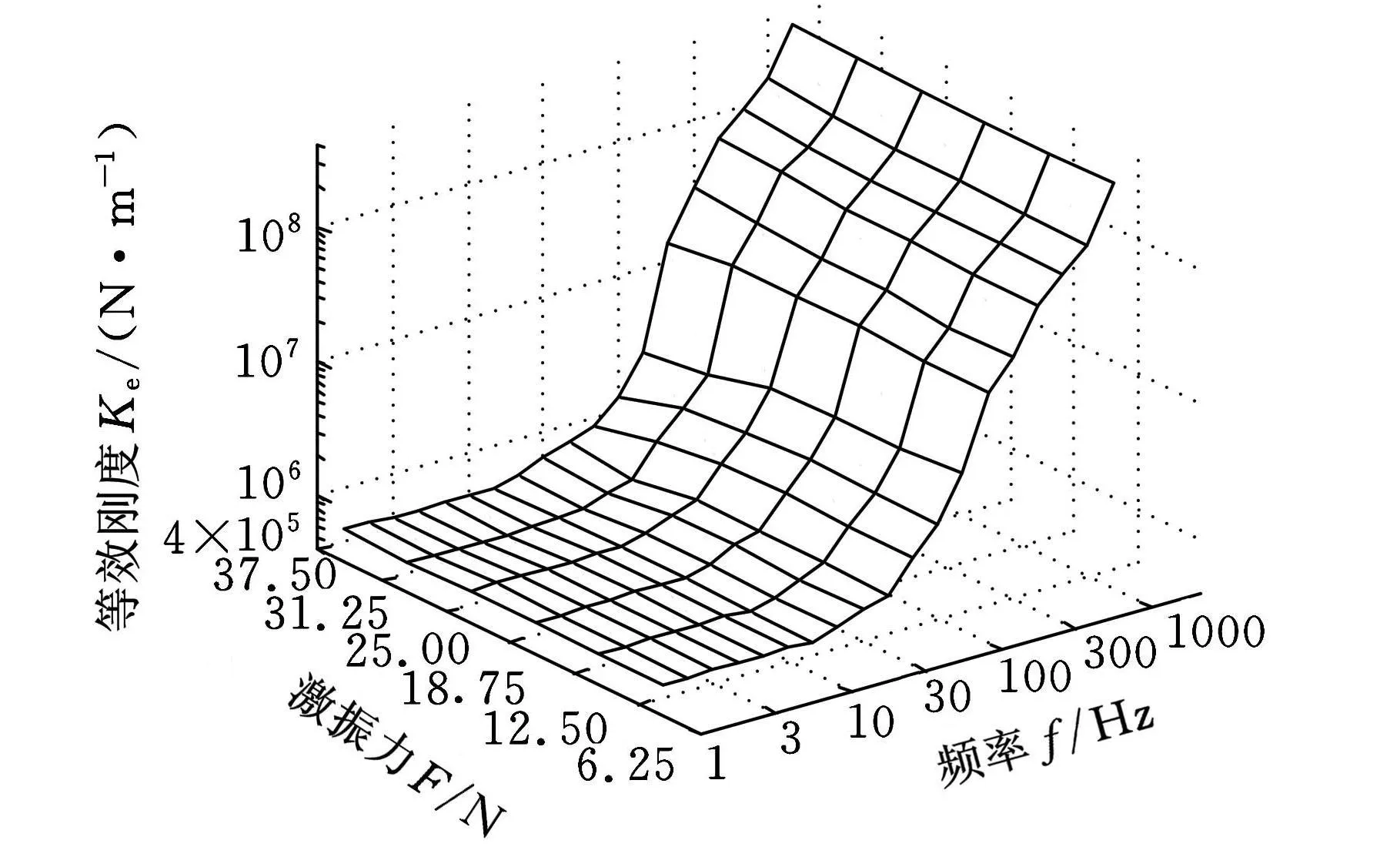
图16 不同激励力对等效刚度影响的测试结果

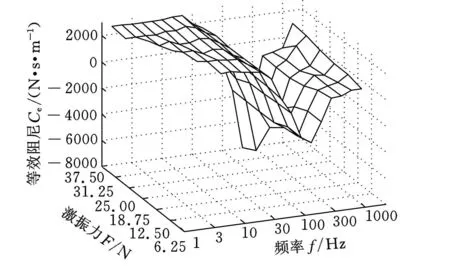
图17 不同激励力对等效阻尼影响的测试结果

根据实验经验,当主动电磁悬浮控制系统能很好平缓低频的小幅激励时,会使得同频位移信号难以检出,导致识别结果不稳定。因此对于激振幅度的选择,在测量10Hz以下的低频刚度阻尼时,需要增大激振力幅度,使振动响应达到可测的水平。对于10Hz以上的频率,激振力幅度的可选范围无具体限制,只要能稳定地保持悬浮状态且振动尚可,均能正常测得系统的等效刚度和阻尼值。

5 结论

本文提出的主动电磁悬浮系统支承特性测试方案,能够在线地实时检测主动电磁悬浮系统在不同频率下的等效刚度和等效阻尼,并能更真实地反映等效刚度和阻尼的实际变化情况。虽然,为了与理论计算比较,实验中仍采用传统的PID控制算法,但是很显然该测试方法与电磁悬浮的控制策略无关。

实验结果表明,本文提出的主动电磁悬浮系统的支承刚度和阻尼的测试方案是可行的,测试结果无论从数值和变化趋势都与理论分析结果相一致,能够方便地在未知控制系统传递函数情况下对主动电磁悬浮系统的支承等效刚度和阻尼进行测定,其结果可以作为主动电磁悬浮系统动力学特性研究的依据,具有较强的实用意义。

[1] Haberman H L.An Active Magnetic Bearing System[J].Tribology International,1980,4：85-89.

[2] Humphris R R,Kelm R D,Lewis D W,et al.Effect of Control Algorithms on Magnetic Journal Bearing Properties[J].Journal of Engineering for Gas Turbines and Power,1986,108(10)：624-632.

[3] 汪希平.电磁轴承系统的刚度阻尼特性分析[J].应用力学学报,1997,14(3)：95-100.

[4] 曹洁.电磁轴承控制系统参数与刚度、阻尼的关系[J].甘肃工业大学学报,1996,22(1)：79-84.

[5] 赵雷,丛华,赵鸿宾.可控磁悬浮轴承刚度与阻尼特性研究[J].清华大学学报,1999,39(4)：96-99.

[6] 胡业发,周祖德,江征风.磁力轴承的基础理论与应用[M].北京：机械工业出版社,2006.

[7] 吴华春,胡业发,江征风.磁力轴承支承特性的影响因素研究[J].组合机床与自动化加工技术,2007(4)：7-10.

[8] 杨作兴,赵雷,赵鸿宾.电磁轴承动刚度的自动测量[J].机械工程学报,2001,37(3)：25-29.