泥石流危险性SIGA-BP 神经网络评价方法及应用

谷秀芝，陈洪凯，刘厚成

（重庆交通大学岩土工程研究所，重庆 400074）

泥石流危险性SIGA-BP 神经网络评价方法及应用

谷秀芝，陈洪凯，刘厚成

（重庆交通大学岩土工程研究所，重庆 400074）

泥石流危险度是由泥石流危险因子综合判定的，然而危险因子有主次之分，要从众多泥石流危险因子中筛选出作用最大的主要危险因子是很困难的，利用自适应免疫遗传算法SIGA（Self-adaptive Immune Genetic Algorithm）对BP神经网络进行优化，获得了与云南省最相关的7项泥石流危险因子，建立了基于SIGA的BP神经网络模型，并对10组泥石流沟数据进行预测，得到了较高的预测结果。

泥石流;神经网络;危险度;危险因子

泥石流对其活动区（包括形成区、流通区和堆积区）内的水土资源、生态环境、经济建设及人民生命财产等会造成直接破坏和危害，而且泥石流的破坏力与其危险性有很大关系。泥石流危险性的评价传统上采用统计分析法［1］。但统计分析法存在评价工作量大、时间长、主观性等问题。近年来，在泥石流的危险性评价中又引入了模糊评价［2-4］、BP神经网络［5-7］等方法，取得了较好的应用效果。但模糊评价的方法中确定隶属度比较困难。基于传统遗传算法［8-11］的BP神经网络则存在BP神经网络输入层难确定、学习过程收敛速度慢、算法不完备、容易陷入局部极小点、神经网络模型的健壮性不好等缺点。

Chang F J 和 Lee S P［12］在泥石流发生区使用GMDH和人工神经网络的方法通过分析瞬时降水的泥石流危险因子来评价泥石流等级，结果表明瞬时降雨不是泥石流发生的唯一危险因子。Chang F J和Hsieh C L［13］调查了影响泥石流的危险因子还包括:主沟长度、流域面积、流域最大相对高差和24 h最大降水量等。刘希林和唐川的泥石流危险性评价［14］中也对泥石流的众多因子进行了分析，给出了影响泥石流的主危险因子和次危险因子，即:在特定地区哪几个泥石流因子与此地区的泥石流危险度评价是最相关的。

针对以上应用于泥石流危险性评价方法中的缺点，本文使用自适应免疫遗传算法的BP神经网络方法，该方法在基本BP神经网络算法的基础上，通过自适应免疫遗传算法的全局寻优能力，并利用云南省泥石流沟的实际数据，对BP神经网络的输入进行优化，最终从10项泥石流危险因子中确定出与云南省泥石流沟最相关的7项泥石流危险因子，并以此进行神经网络的学习，建立关于泥石流危险性评价的简单、快速和方便的分析模型，利用该模型对云南省10条泥石流沟进行泥石流危险度评价，达到了较高的预测精度。预测结果证明该方法是解决泥石流危险性评价问题的一种新思路。

1 泥石流危险性SIGA-BP神经网络评价方法

1.1 BP神经网络

BP神经网络是一种单向传播的多层前向网络，网络除输入输出节点外，还有一层或多层的隐含节点，同层接点中没有任何耦合。输入信号从输入节点依次传到各隐层节点，然后到输出节点，每一层节点的输出只影响下一层的输出［15］，如图1。

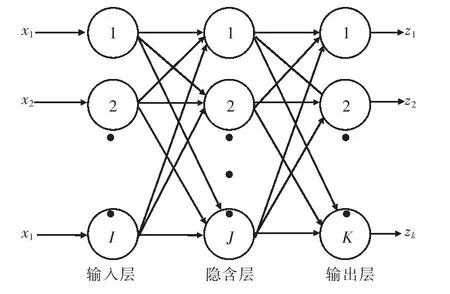
图1 BP神经网络结构Fig.1 BP neural network structure

在确定了BP神经网络的结构后，要通过输入和输出样本集对网络进行训练，亦即对网络的阈值和权值进行学习和修正，以使网络实现给定的输入输出映射关系。

BP网络的实现过程分两个阶段:

第1阶段是输入已知学习样本，通过设置的网络结构和前一次迭代的权值和阈值，从网络的第一层向后计算各神经元的输出。

第2阶段是对权和阈值进行修改，从最后一层向前计算各权值和阈值对总误差的影响（梯度），据此对各权值和阈值进行修改。

1.2 SIGA-BP神经网络

SIGA-BP神经网络是自适应遗传算法与BP神经网络的有机结合，利用自适应遗传算法全局搜索能力强的特点［16］，先用遗传算法对BP网络的权值和阈值进行全局粗精度的预学习，定位最优解区域，使得权值和阈值种群聚集在参数解空间的某几处，再利用BP算法对局部搜索的有效性在这些小的解空间中进行梯度细搜索［17-18］，最终求得最优解。

1.2.1 SIGA-BP 的实现方法

1）编码方案

对网络中连接权值和阚值进行编码，每一个基因码链个体代表权值和阈值取特定值的神经网络，方法有两种:一是采用二进制编码方案，另一种是采用实数编码方案。

2）适应度函数

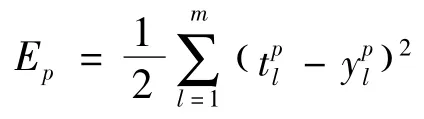
3）遗传算子

对于不同的问题，遗传算子的形式多种多样，其中交叉率Pc和变异率Pm值能够随适应度自动改变。当种群各个体适应度趋于一致或者趋于局部最优时，使Pc和Pm增加，而当群体适应度比较分散时，使Pc和Pm减少。同时，对于适应值高于群体平均适应值的个体。对应于较低的Pc和Pm，使该解得以保护进入下一代:而低于平均适应值的个体，相对应于较高的Pc和Pm使该解被淘汰掉。

4）网络结构的进化

神经网络结构的进化主要包括两方面的内容:①网络的拓扑结构;②节点转移函数。目前，网络结构参数的决定主要由经验来决定，缺乏系统和严格的理论指导，可引进SIGA来设计网络结构并根据性能评价准则，可优化网络结构。

1.2.2 SIGA-BP 计算过程

1）确定种群大小N和种群个体长度l，随机生成种群，并将种群的个体进行二进制编码，最后确定出基因和染色体结构;

2）设置自适应免疫遗传算法的参数以及神经网络所需要的参数，并把基因解码为神经网络结构;

3）用神经网络计算适应度函数并作选择，把得到的结果和实际结果进行比较，并把两者比较的均方差作为适应度函数的返回值，如果两者差距很大，就继续进行遗传变异，算法退到第二步，直到两者的误差达到所设定的误差范围以内时，算法转到下一步;

4）最后获得与泥石流沟最相关的泥石流评价因子，以作为BP神经网络的输入;

5）用学习好的网络对要识别的样本进行分析，最后得到要识别样本的泥石流风险度等级。

2 SIGA-BP神经网络的具体结构

2.1 样本的选择

本文选取文献［14］中云南省20条泥石流沟的200个基础数据为训练样本，建立了基于SIGA-BP神经网络的泥石流危险度评价模型。针对泥石流危险度评价的10项评价指标，利用SIGA-BP神经网络的泥石流评价模型，根据给出的云南省泥石流沟的具体数据，得到与云南省各沟最相关的泥石流评价指标，在20组评价指标中任选15组作为训练数据集，但要保证每个县、市至少有1组数据参与训练，剩余的5组评价指标作为测试数据集。

2.2 SIGA-BP神经网络评价指标的选取

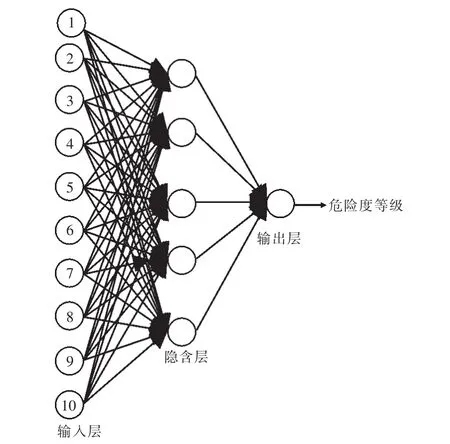
图2 三层BP神经网络Fig.2 Three BP neural network

2.3 SIGA的编码及参数选择

SIGA遗传算法采用Matlab 7.0的gads工具箱。

SIGA染色体采用14位的二进制编码，前10个码表示泥石流的10个评价指标，0表示不作为BP神经网络的输入，1表示作为BP神经网络的输入;下面3个表示隐含层的神经元数:即101，最后一个码是激活函数:0表示tansig，1表示logsig。

使用Matlab 7.0中的trainlm对学习样本进行学习，要求学习误差MSE达到0.001%，最大的迭代次数为3 000。

2.4 SIGA-BP神经网络的优化结果

经过30代遗传变异后，适应度函数返回值最优值为0.848 69，即校验样本的预测值与实验值的均方差。获得了最优染色体为1101110110 101 1。解码得到与云南省的泥石流最相关的评价指标为:一次泥石流（可能）最大冲出量、泥石流发生频率、流域面积、主沟长度、流域最大相对高差、单位流域切割密度、24 h最大降水量。激活函数使用logsig，并对剩下的5条泥石流沟的测试数据集进行泥石流等级评价。

3 实例应用

3.1 样本数据

首先需要对各条泥石流沟的因子进行归一化处理。由于这些因子都是优性因子（数据越大，对泥石流活动性贡献越大），采用如下公式计算:

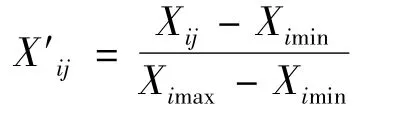
式中:Xij为第j条泥石流沟的第i个指标的原始值;Ximin和Ximax分别为所有泥石流沟第i个指标的最小值和最大值。

归一化处理的结果如表1。

表1 云南省20条泥石流沟数据Tab.1 Data of 20 debris flow dates in Yun Nan

（续表1）

3.2 基于SIGA神经网络的泥石流危险度评价模型

从上述20组中任选15组数据作为样本数据作为SIGA-BP神经网络的输入数据进行训练，并对剩下的5条泥石流沟测试数据集进行泥石流等级评价。最后获得了与云南省最相关的7项泥石流评价指标，并建立了基于SIGA神经网络的泥石流危险度模型，在最相关的指标基础上对云南省10组数据样本进行预测，结合泥石流危险度等级划分表［14］（表2）得出其危险度等级，如表3。从表3中可以看出，SIGA-BP神经网络对泥石流危险度的预测值与实际观测值很接近，与AHP法相比其相对误差均在±3%范围内，因此利用对特定地区学习好的神经网络对该区的泥石流沟进行危险度评价，可取得符合实际的结果，据中国科学院东川泥石流研究观测站的观测资料，蒋家沟每年向小江输送泥沙200～300万m3，最大量高达600多万m3。该沟泥石流至今已有300余年的历史，其以每年爆发次数多，规模大，历时长和危害大而独具代表性，被誉为“泥石流的天然博物馆”［20］，评价结果也表明蒋家沟泥石流属于极度危险区。

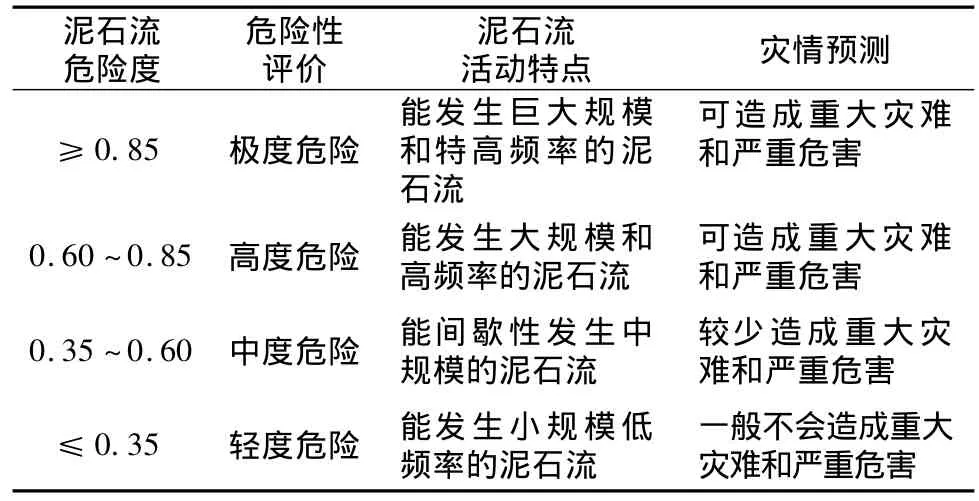
表2 泥石流危险等级划分Tab.2 Hazard degree of debris flow

表3 实例评价指标及评价结果Tab.3 Examples of evaluation indicators and evaluation results

4 结论

1）将自适应遗传算法SIGA用于BP神经网络建模，对建立BP神经网络结构起到了很好的全局寻优作用;

2）由于现在对于泥石流危险度评价指标的不一致性，本文利用基于SIGA-BP神经网络方法来选择与云南省相关的泥石流危险度评价指标，且指标为:一次泥石流（可能）最大冲出量、泥石流发生频率、流域面积、主沟长度、流域最大相对高差、单位流域切割密度、主沟床弯曲系数、泥砂补给段长度比、24 h最大降水量、流域内人口密度。

3）从20组中任选15组数据作为SIGA-BP神经网络的输入数据，并对SIGA-BP神经网络进行训练。最后获得了与云南省最相关的7项泥石流评价指标，并建立了基于SIGA神经网络的泥石流危险度模型，并对云南省10条泥石流沟进行预测，结果显示预测值与实测值很接近，其相对误差均在±3%范围内，达到了较高的预测精度。

［1］ Gazendam H，Liu K.The evolution of organizational semiotics:a brief review of the contribution of Ronald stamper［EB］.2004-04-18，http://www.orgsem.org/papers/00.pdf.

［2］ 刘章军.基于模糊概率方法的泥石流危险性评价［J］.三峡大学学报:自然科学版，2007，29（4）:295-298.

［3 ］ ZHAO Dong-mei，MA Jian-feng，WANG Yue-sheng.Model of fuzzy risk assessment of the information system［J］.Journal on Communication，2007，28（4）:51-56.

［4］ 王学武，石豫川.多级模糊综合评判方法在泥石流评价中的应用［J］.灾害学，2004，19（2）:2-6.

［5］ 鲁小兵，李德基.基于神经网络的泥石流预测［J］.自然灾害学报，1996，5（3）:47-50.

［6］ 赵源，刘希林.人工神经网络在泥石流风险评价中的应用［J］.地质灾害与环境保护，2005，16（2）:135-138.

［7］ 刘希林，苏鹏程.四川省泥石流风险评价［J］.灾害学，2004，19（2）:23-28.

［8］ 陈刚，何政伟，杨洋，等.基于径向基函数神经网络的泥石流危险性评价［J］.计算机应用研究，2009，26（1）:241-243.

［9］ 汪明武.基于神经网络的泥石流危险度区划［J］.水文地质工程地质，2000，27（2）:18-19.

［10］ 李发斌，崔鹏，周万村，等.用遗传神经网络分析泥石流活动性［J］.中国地质灾害与防治学报，2003，14（3）:16-19.

［11 ］ CHANG Tung-chiung，CHEN Yue-hone.The application of genetic algorithm in debris flows prediction ［J］.Environ Geol，2007，5（3）:339-347.

［12］ Chang F J，Lee S P.A Study of the Intelligent Control Theory for the Debris Flow Warning System ［R］.Proceedings of the 1stDebris Flows Conference.Taipei，Taiwan，ROC，1997:109-123.

［13］ Chang T C，Hsieh C L.Site investigation and analysis for debris flows in eastern Lan-Yun District［J］.Chinese Water and Soil Reserveation Report Taiwan 1996，27（2）:139-150.

［14］ 刘希林，唐川.泥石流危险性评价［M］.北京:科学出版社，1995:3-15，62-65.

［15］ 汪茜，李广杰.基于人工神经网络的磐石市泥石流预测.［J］.人民长江，2009，40（3）:47-48.

［16］ 乔立杰，唐常杰.SIGA:一种新的自适应免疫遗传算法［J］.中山大学学报，2008，47（3）:6-9.

［17］ CHANG Tung-chiung.Risk degree of debris flow applying neural networks ［J］.Nat Hazards，2007，42（1）:209-224.

［18 ］ CHANG Tung-chueng，CHAO Ru-jen.Application of back-propagation networks in debris flow prediction ［J］.Engineering Geology，2006，49（7）:270-280.

［19］ 田景文，高美娟.人工神经网络算法研究及应用［M］.北京:北京理工大学出版社，2006:24-39，64-65.

［20］ 丁明涛，韦方强.云南蒋家沟泥石流成因及其防治措施探析［J］.水土保持研究，2008，15（1）:20-21.

Method and Application of Debris Flow Hazard Assessment Based on SIGA-BP Neural Network

GU Xiu-zhi，CHEN Hong-kai，LIU Hou-cheng
（Institute of Geotechnical Engineering，Chongqing Jiaotong University，Chongqing 400074，China）

The risk degree of debris flow is determined by dangerous factors of the debris flow.The dangerous factors are divided into primary and secondary factors.It is difficult to choose the most dangerous factor.BP neural network is optimalized by self-adaptive immune genetic algorithm（SIGA），and seven dangerous factors of Yunnan province are obtained.SIGA-BP neural network is also established，which is applied to forecasting data of 10 groups’debris flow，and more accurate forecasting results are obtained.

debris flow;neural network;risk degree;risk factors

中国分类号:P642.23

A

1674-0696（2010）01-0098-05

2009-06-30

国家自然科学基金项目（50678182）;中国博士后科学基金项目（20080430095）

谷秀芝（1982-），女，河北邢台人，硕士研究生，主要从事地质灾害与防治研究。E-mail:gxzh1982@126.com。

book=102,ebook=68