钢管混凝土拱桥拱肋吊装线形控制的分步算法

赵 洋，周水兴，刘 静

（1.重庆交通大学 土木建筑学院，重庆 400074;2.重庆市巫山县交通勘察设计室，重庆 404700）

钢管混凝土拱桥拱肋吊装线形控制的分步算法

赵 洋1，周水兴1，刘 静2

（1.重庆交通大学 土木建筑学院，重庆 400074;2.重庆市巫山县交通勘察设计室，重庆 404700）

针对钢管混凝土拱桥拱肋分节段安装由扣索张拉引起的高程差问题，以裸拱自重变形后的拱轴线形为控制目标，基于最优化理论和一次扣索张拉法，提出先用零阶优化法按整体安装计算出各拱肋节段的预抬量和扣索索力，再以整体安装计算结果为目标，根据拱肋节段安装顺序，通过迭代方法计算出各个节段安装时的预抬量和扣索索力。将该算法应用到主跨240 m的巫山新龙门大桥拱肋安装线形控制中，松索成拱后的线形与目标线形吻合良好。

钢管混凝土拱桥;分步算法;线形控制;零阶优化法;整体安装

钢管混凝土拱桥是一种典型的自架设体系结构，与其它自架设体系桥梁（如斜拉桥）不同，结构的线形和应力不能在成桥后再作调整，也不能像连续梁桥或连续刚构桥，节段标高可在浇筑阶段做适当调整，钢管混凝土拱桥在整个施工过程中轴线调整是非常有限的［1-2］。

目前，绝大多数钢管混凝土拱桥拱肋施工采用无支架缆索吊装千斤顶斜拉扣挂法［2-3］，将拱肋沿纵向划分为若干段进行架设，合龙时以裸拱自重变形后的拱轴线线形为控制目标。受到缆索起重能力的限制，一般采取分节段逐段吊装，待相邻两个节段安装就位并调整高程后，焊接接头钢板形成整体节段，然后安装拱肋间平联。针对钢管混凝土拱桥拱肋安装施工控制已经提出了不少方法，如前进迭代法［4-5］、定长扣索法［6］、优化法［7-8］等。这些方法各有侧重点，其共同点都是针对拱肋整段安装提出的，均未对拱肋分节段安装的预抬量和扣索索力计算开展研究。在拱肋分节段安装时，由于扣索张拉会影响到先前安装节段的高程，如果按整体安装方法得到的索力来张拉，势必造成拱肋间高程不一致，导致主拱受力不均匀，严重时还会造成主拱肋横向偏位。因此，如何确定拱肋各个节段安装的初始预抬高量和扣索索力是钢管混凝土拱桥分节段安装线形控制的关键。

本文以裸拱自重变形后的拱轴线形为控制目标，基于最优化理论和一次扣索张拉法，提出先用零阶优化法按整体安装计算出各拱肋节段的预抬量和扣索索力，再以整体安装计算结果为目标，根据拱肋节段安装顺序，通过迭代方法计算各个节段安装时的预抬量和扣索索力。文中提出的方法在新龙门大桥拱肋安装中得到成功的应用。

1 拱肋吊装线形控制理论

1.1 拱肋整体安装优化计算的数学模型

理论上讲，总会存在一组合理的节段预抬量和相应的扣索索力，使松索成拱后的拱肋线形与设计期望线形（裸拱自重变形后的线形）偏差降到最小。实际分析时，只能取若干个点来分析，通常取高程观测点来代替。本文以拱肋各高程观测点的高程与相应位置的期望高程的偏差的平方和最小为优化目标，以观测点的实际位移为设计变量，索力及控制截面的应力值为状态变量来建立优化模型。

设最优化问题［9］为:

式中:s为各组扣索索力组成的向量;uj（s）为拱轴线上观测点的实际位移值;为拱轴线观测点上的期望位移;L为扣索钢绞线的根数;Np为单根钢铰线的屈服力;k为安全系数;和分别为各观测点实际位移和期望位移偏差的上下限;σj为结构单元的最不利组合应力;σ为钢材的容许应力。

由式（1）可知，理想的情况是通过张拉扣索使拱轴线全盘达到期望线形，但实际上是无法做到的。因为期望位移主要是由结构自重引起的，它是分布载荷，而索力为点荷载，因此只能使其偏差平方之和最小而且各观测点的偏差控制在JTJ041-2000《公路桥涵施工技术规范》要求范围内，这样得到的拱肋线形就可满足施工要求。

使用零阶分析法通过对目标函数添加罚函数将有约束多变量非线性规划问题变成无约束非线性规划问题，即将原目标函数f（）x增广为一个新的函数:

式中:f0为参考目标函数;q为惩罚因子;px为设计变量的外罚函数;pg、ph、pw为状态变量的混合罚函数［10］。

计算迭代步骤采用以下方法:这里，sk是采用黄金分割法和最小二乘法来确定的参数，其对应的搜索方向d（）k用共轭方向法［11］确定，迭代公式如下:

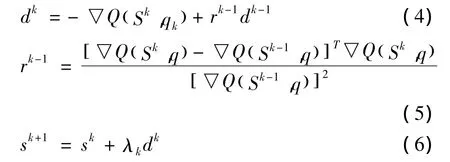
最优化计算时的收敛准则如下:

τ为目标函数的允差。

1.2 计算思路

本计算分3个阶段进行:裸拱自重变形计算、整体安装计算和分节段安装计算。以制作拱形为基础建模，总体计算思路如图1。

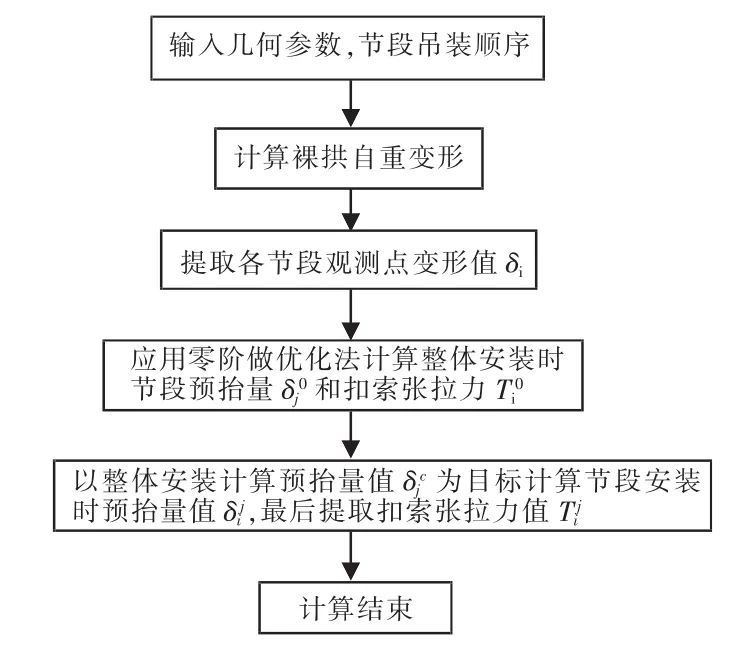
图1 总体计算思路Fig.1 General computing ideas

2 工程应用

2.1 工程背景

巫山新龙门大桥是一座计算跨径为240 m的中承式钢管混凝土拱桥，矢跨比1/5，拱轴系数m=1.5，每条拱肋由4根Φ1 016 mm×14 mm的钢管组成，腹杆采用Φ500 mm×10 mm空钢管，拱肋之间用K撑钢管连接，上下弦管内和缀板之间压住C50微膨胀混凝土。

新龙门大桥拱肋采用缆索吊装斜拉扣挂法施工。拱肋安装时采用两岸对称悬拼，拱肋每半跨分6个吊段，吊段最大重量约60.7 t（不含扣点重量）。1、2、3、4#扣索经扣塔索鞍转向锚固于张拉台，5、6#扣索经主塔索鞍转向后也锚固于张拉台（图2）。采用单节段吊装，待上下游同一节段安装就位后，安装节段间连接横撑，即完成一个双肋节段的安装。

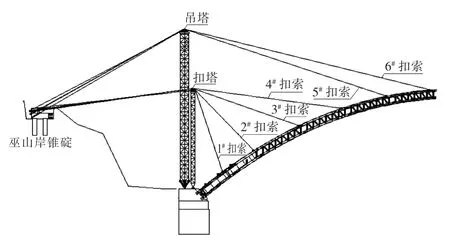
图2 新龙门大桥吊装系统（巫山岸）Fig.2 New Long-men bridge lifting system（Wushan bank）

2.2 模型单元设定与参数选择

采用ANSYS11.0有限元程序建模，拱肋、塔架、K撑等用Beam 44空间梁单元模拟，扣索单元用Link 10单元模拟。

扣锚索张拉的时候伸长量被油压千斤顶收回，使得扣锚索固定端沿轴向方向移动。在ANSYS程序计算中，采用对扣锚索降温来实现张拉的模拟，将每节段悬臂端点的竖向位移值作为设计变量;扣索的索力、钢管拱肋内的应力和变形等均是欲约束的变量，将其设置为状态变量;将每节段悬臂端点的实际高程与设计高程差的平方和最小作为目标函数，来评价最优化计算的逼近程度;目标函数中各观测点期望竖向位移，取为各观测点的施工预拱度，拱肋标高允许偏差的上下限、分别取 +0.5 cm、-0.5 cm。

2.3 裸拱自重变形计算

由于拱肋制作时计入了预拱度值，因此，相应的裸拱有限元模型也应计入预拱度值。通过计算，得到表1中各观测点的变形。

表1 各观测点裸拱自重变形值Tab.1 Weight deformation of the observation stations

2.4 整体安装计算

整体安装计算模拟新龙门大桥拱肋吊装顺序如图3。

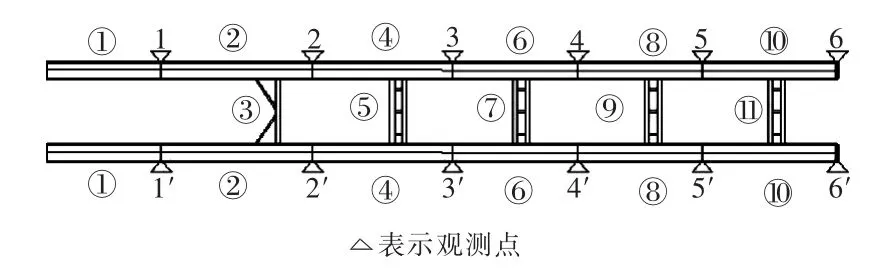
图3 巫山岸整体安装计算顺序Fig.3 Calculation sequence of global installment（Wushan bank）

将上述理论和方法编写成APDL命令流，利用ANSYS11.0的结构分析功能和零阶优化功能，计算新龙门大桥的钢管拱肋吊装过程中的整体安装预抬量与扣索索力，并考虑结构几何非线性的影响，按应力叠加法考虑了拱桥的实际施工过程。通过计算，各观测点变形与节段预抬量分别如表2、表3。

表2 整体安装变形值Tab.2 Deformation of global installment

表3 各节段整体安装预抬量值Tab.3 Pre-camber of segments in global installment

2.5 分节段安装计算

分节段安装计算阶段模拟新龙门大桥拱肋安装顺序如图4。

图4 巫山岸分节段安装计算顺序Fig.4 Calculation sequence of installing segments（Wushan bank）

取典型节段具体计算流程如图5。

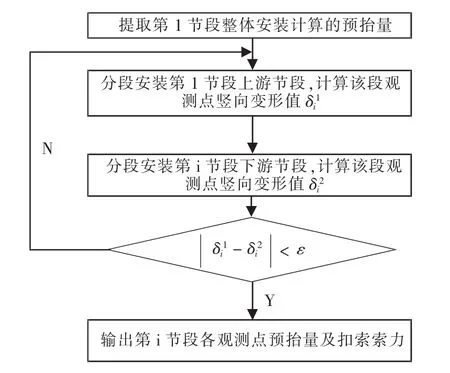
图5 典型节段分段计算流程Fig.5 Calculation sequence of installing typical segments

通过计算，各节段初始预抬量与初始张拉力为如表4数据时，预抬量与扣索索力可达整体安装阶段的预抬量与扣索索力。

表4 分节段安装初始预抬量与扣索初始张拉力Tab.4 Deformation and cable forces of installing segments

3 线形控制结果

施工线形控制的好坏，可以从合龙条件是否理想来衡量。新龙门大桥合龙前数据（以巫山岸为例）如表5。

表5 巫山岸合龙前数据（巫山岸）Tab.5 Datasheet before rib installation closure（Wushan bank）

从表中数据看，在合龙前，拱肋各个控制点的实测标高和理论计算高程值差距较小，基本控制在±1 cm以内（由于扣索安全系数取值较小，故6#节段扣索未张拉到位），且实测标高数据中未扣除温度、扣索锚固段松弛、主塔塔偏等因素影响;横向不同节段间高程相平，很好地解决了后续节段安装对已安装节段影响的问题;轴线偏位也在JTJ041-2000《公路桥涵施工技术规范》要求控制范围内。因此可以说，新龙门大桥拱肋吊装的线性控制效果非常理想。

4 结论

随着科学技术发展，大跨径钢管混凝土拱桥施工会出现更多的新方法和新工艺，对于大跨径钢管混凝土拱桥分节段吊装线形控制还有很多问题值得研究。在新龙门大桥的成功实践表明，笔者基于最优化理论，采用零阶优化法计算预抬高量和扣索索力的方法，能够真实地模拟钢管拱肋吊装过程，准确的把握施工过程中的各个敏感参数并进行控制，解决了分节段吊装中节段高程调平的难题，并使得施工组织简单、有效，取得的控制效果也非常理想，可供钢管混凝土拱桥拱肋分段吊装施工控制参考。

［1］ 顾安邦.桥梁工程（下册）［M］.北京:人民交通出版社，1999.

［2］ 罗乐静.大跨度钢管混凝土拱桥施工控制研究［D］.南宁:广西大学，2004.

［3］ 向中富.桥梁施工控制技术［M］.北京:人民交通出版社，2001.

［4］ 牛润明，段树金.大跨度钢管混凝土拱桥拱肋吊装过程仿真分析［J］.城市道桥与防洪，2004（2）:64-66.

［5］ 袁海庆，范小春，范剑锋，等.大跨度钢管混凝土拱桥拱肋吊装预测的迭代前进算法［J］.中国公路学报，2003，16（3）:48-57.

［6］ 周水兴，熊洪滨，蔡净.定长扣索法安装拱桁架节段控制索力计算［J］.工程力学，2001，（增刊）:838-842.

［7］ 张建民，郑皆连，秦荣.大跨度钢管混凝土拱桥吊装过程的优化计算方法［J］.桥梁建设，2002（3）:52-58.

［8］ 张治成.大跨度钢管混凝土拱桥施工控制研究［D］.杭州:浙江大学，2004.

［9］ 张治成，叶贵如，王云峰.大跨度拱桥拱肋线形调整中的扣索索力优化［J］.工程力学，2004（12）:187-192.

［10］ 颜东煌，刘光栋.确定斜拉桥合理施工状态的正装迭代法［J］.中国公路学报，1999，12（2）:59-64.

［11］ 汪树玉，杨德栓，刘国华.优化原理、方法与工程应用［M］.杭州:浙江大学出版社，1991:243-258.

Step-by-Step Algorithm of Liner Control of Arch Ribs of CFST Arch Bridges

ZHAO Yang1，ZHOU Shui-xing1，LIU Jing2
（1.School of Civil Engineering ＆ Architecture，Chongqing Jiaotong University，Chongqing 400074，China;
2.Traffic Survey＆ Design Station of Wushan County in Chongqing，Chongqing 404700，China）

concrete-filled steel tubular（CFST）arch bridge;step-by-step algorithm;liner control;zero-order optimization method;global installment

U448.22

A

1674-0696（2010）01-0001-03

2009-09-28

交通部西部交通科技项目（200631881422）

赵 洋（1984-），男，河南驻马店市人，硕士研究生，主要从事大跨度桥梁设计与施工控制技术研究。E-mail:zhaoyang8526@163.com。

Aiming at the problem of height difference caused by the cable tension in segment installation of CFST arch ribs，the zero-order optimization method to calculate the pre-lift capacity and cable forces of each arch rib section in global installation is put forward，which takes the deformed arch axis caused by rib self-weight as the control objective，using the optimization theory and one-time cable tension method.Then，taking the results of global installation as objective，the pre-lift capacity and cable forces of every segment in installation are calculated by iteration algorithm，according to installation sequence of arch rib segment.The algorithm is applied to the arch axis control for New Long-men Bridge with 240m span in Wushan.It is showed that the arch axis under released cables is in well accordance with the expecting ones.