草履蚧若虫空间分布型及抽样技术研究初报

宁豫婷，李俊中，方松山，李玉峰，王庚申，邢占兵



草履蚧若虫空间分布型及抽样技术研究初报

宁豫婷1，李俊中1，方松山1，李玉峰1，王庚申2，邢占兵3

（1.许昌市森防站，河南 461000；2.焦作市森防站；3.禹州市森防站）

采用聚集度指标、分布型检验等方法测定并分析草履蚧空间分布型，结果表明：草履蚧若虫在林间呈聚集型的负二项分布，聚集原因是由环境条件引起的，其个体间相互吸引。同时，应用Iwao统计方法，计算了不同种群密度下最适抽样数及序贯抽样。

草履蚧；空间分布型；抽样技术

草履蚧（Kuwana）属同翅目，珠蚧科。在我市1年发生1代，以卵囊在树下表土中越冬，以若虫和雌成虫刺吸枝芽危害。主要为害杨树、泡桐、刺槐等20多种林木、果树及花灌木，影响树木正常展芽抽枝，使叶片提早变黄、脱落，树势逐渐衰弱，严重时造成树木死亡。为提高草履蚧预测水平，准确指导防治，2006年3月对草履蚧空间分布型进行了初步研究，现将结果报道如下。

1 试验地概况

试验地设在禹州市顺店镇南辕庄、杜村，均台办连路弯村杨树片林内，杨树品种为46杨，树龄3~4 a生，株行距2 m×3 m，管理水平一般，草履蚧历年发生较重。

2 材料与方法

2.1 调查方法

在试验地上随机选择30株树，于3月下旬草履蚧若虫2~3龄进行调查，每株树分东、南、西、北4个方位，每方位分上、中、下3层，将每株树划分为12个资源单位，每个资源单位调查20 cm长的枝条1枝，记载草履蚧数量，每个试验地共调查360个枝条。3块试验地共选择90株树，1 080个枝条进行调查。

2.2 分析方法

2.2.1方差分析 根据东、西、南、北和上、中、下不同部位调查的数据进行方差分析。

2.2.3空间分布型适合度卡方（X2）检验[1]

将调查获得的数据列成频次分布表，进行频次分布检验，求得泊松分布、奈曼分布和负二项分布的理论频次，与实际频次相比较，进行卡方检验，确定其所属分布型。

2.2.4聚集原因分析[2]用Blackith（1961）提出的聚集均数（λ）分析害虫的聚集原因。公式为：

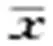
2.3 抽样技术研究

2.3.1理论抽样数的确定[3]

根根据平均虫口密度和允许误差确定合理取样数。计算方式为：

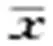
2.3.2序贯抽样的应用[2]

T0（n）=nmo

3 结果与分析

3.1 方差分析

草履蚧若虫在杨树树冠的分布方差分析结果见表1。

表1 草履蚧不同方位方差分析

从表1可见，草履蚧若虫在杨树树冠的东、西、南、北分布差异不显著，上部、中部、下部分布有显著性差异。

3.2 Iwao:m*-回归分析

3.3 分布型检验

根据泊松分布、奈曼分布、负二项分布的概率计算公式，求得理论频次与调查频次比较，进行卡方（X2）检验（见表3），确定其所属分布型。

从表2卡方（X2）检验结果表明，用泊松分布、奈曼分布概率公式计算所得卡方值均较大，远大于相应自由度下时的P0.01卡方值，说明草履蚧空间分布型不属于泊松分布和奈曼分布。用负二项分布概率公式计算所得卡方值小于相应自由度下时的P0.05５卡方值，证明草履蚧空间分布型属于负二项分布。

表2 草履蚧分布型检验

3.4 聚集原因分析

用Blackith（1961）聚集均数分析草履蚧若虫分布的聚集原因。

由于草履蚧若虫2K自由度为小数，需要用比例内插法计算r值，再计算λ值，经计算λ=0.528 。λ值小于2，说明草履蚧若虫聚集分布的原因主要是由环境条件引起的。

3.5 抽样技术研究

3.5.1合理抽样数的确定

按Iwao空间分布型的统计方法，求得草履蚧若虫α=0.044，β=3.289，在各种密度（每30 cm长枝的草履蚧若虫数）下最适抽样模型为

根据上面公式计算理论抽样数（见表3）。

由表3看出，同一误差水平下，随若虫种群密度增加抽样数相应减少；在同一种群密度水平下，允许误差越大，抽样数越少。

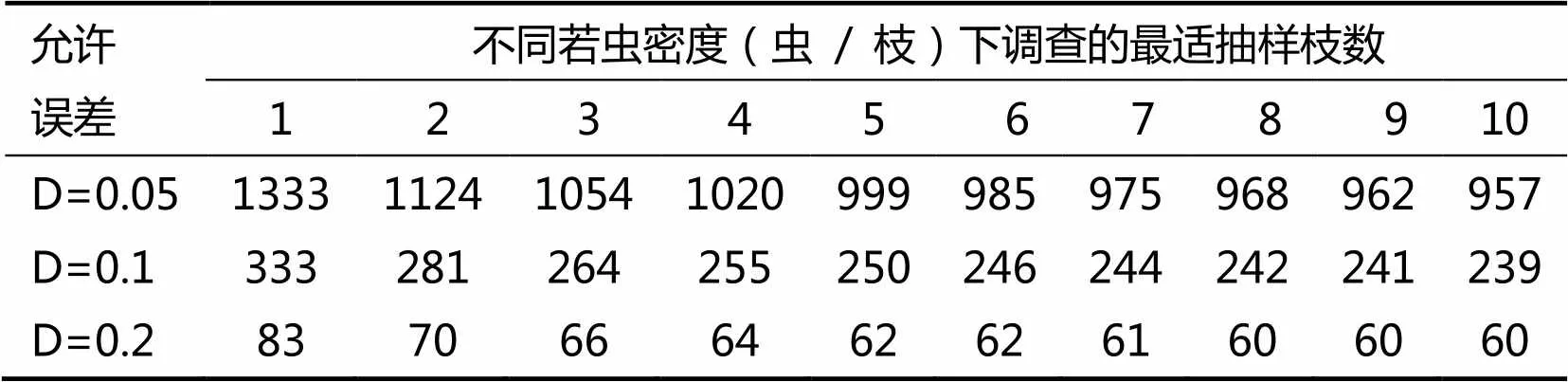
表3 草履蚧若虫不同密度下的最适抽样数

3.5.2 Iwao序贯抽样

根据Iwao空间分布型的统计方法，草履蚧若虫α和β系数分别是0.044和3.289， 取t=1, 在序贯抽样中，要拟定防治虫口密度，初步拟定草履蚧防治指标为3个若虫/30cm长枝（草履蚧防治指标尚未确定），即m0=3，根据计算公式制定序贯抽样分析表（见表4）。

表4 草履蚧若虫序贯抽样分析

从表4可以看出，如果林间调查5枝的累积若虫数超过26头，则需要防治，累积若虫数少于4头时，则不需要防治；若累积若虫数在上下限之间时，往下继续抽样，直到累积若虫数大于上限或小于下限时为止；若累积若虫数仍在上下限之间不宜下结论时，则需确定一个最大抽样数。其计算公式为：

Nmax=t2/d2[(α+1)m0+(β-1)m02]

式中：取t=1，d为调查虫口密度允许误差，取d=0.25，m0=3头/枝，α=0.044，β=3.289，代入上式得

Nmax＝12/0.252[（0.044+1）×3+(3.289-1)×32]=379.728≈380(枝)。

即最大抽样数为380枝。

4 小结与讨论

草履蚧若虫在杨树树冠的东、西、南、北分布差异不显著，上、中、下部分布有极显著性差异。空间分布型结果显示，草履蚧若虫在杨树林内呈聚集分布，这正符合该虫若虫喜聚集在嫩芽刺吸枝芽危害的习性，草履蚧空间分布型属于负二项分布；草履蚧若虫个体间相互吸引，分布的基本成分是个体群；聚集分布的原因主要是由环境条件引起的。

在了解草履蚧若虫空间分布格局的基础上，对抽样技术进行了研究，确定了合理抽样数、序贯抽样表和最大抽样数。

本研究只对草履蚧若虫在树上分布进行了调查分析，还有待对地下草履蚧卵的分布进行调查分析。

[1]徐汝梅.昆虫种群生态学[M].北京：北京师范大学出版社 1987.

[2]张安盛，冯建国，于毅，等.桃粉蚜种群消长动态和空间分布型研究[J].山东农业大学学报自然科学版，2004，35（1）：75-78.

[3]薛贤清.森林害虫预测预报[M].北京：中国林业出版社 1992.

2010-03-26

S763.35

A

1003-2630（2010）01-0021-02

（责任编辑：王团荣）