基于不同应力环境的地基变形计算

陈新苗

（安徽省水利水电勘测设计院 蚌埠 233000）

1 前言

地基的最终沉降量是指地基土层在建筑物荷载作用下不断产生压缩直至变形稳定后地基的沉降量。计算地基最终沉降量的目的是为了在工程设计中或者在地基处理完成后预测该建筑物建成后将产生的最终沉降量、沉降差、倾斜和局部倾斜，并判断地基变形值是否超出允许的范围，以便在工程设计时为采取相应的工程措施提供科学依据，以及在地基处理后用于评价地基加固效果是否达到设计要求，从而保证建筑物的安全。

2 地基土变形机理分析

土的固结压缩规律非常复杂，它不仅取决于土的类别和状态，也随土的边界条件、排水条件和受力方式等因素而异。粘性土与无粘性土的变形机理不同，二相土与三相土的固结过程迥然有别，三相土中由于含气体，变形指标不易准确测定，状态方程的建立与求解都很复杂。天然土体一般都是各向异性、非均质或成层的，这对变形都有较大影响。对地基土来说，上部结构施加的通常都是局部荷载，在固结过程中，除上下方向的排水压缩外，同时还有不同程度的侧向排水与膨胀。

天然土体一般由三相组成，即矿物颗粒构成土的骨架，土骨架孔隙内充填有水和空气。土体受到外力作用后，土粒和孔隙中的流体均会发生位移。土粒本身和孔隙中的水、气压缩量很小，可忽略不计，但在外力作用下，土体中土粒间原有的联结可能受到削弱或破坏，从而产生相对的移动，土粒重新排列，相互挤紧从而导致土体孔隙中的部分水、气被排出，土的孔隙体积便因此缩小，导致土体体积变小，其压缩量随时间增长的过程，称为土的固结。固结问题和固结特性是作为多相介质的土体所特有的区别其他工程材料的一个独特性质。

对一般地基土而言，通常所说的地基沉降都是指固结沉降，目前在工程中广泛采用的计算方法是在无侧向变形条件下的单向压缩分层总和法，首先确立应力——应变关系，广泛采用材料力学中的广义虎克定律，即土体的应力与应变假定为线性关系，这里的压缩模量Es或变形模量E0（三维条件下还有土的侧膨胀系数即泊松比μ）均相当于虎克定律中的杨氏模量。但土体毕竟不是理想弹性体，从土的室内压缩试验中的土的回弹、再压曲线可知，土体的变形是由弹性变形和塑性变形两部份组成，所以回弹曲线与再压曲线能构成一个迥滞环，同时应力的状态、大小以及排水条件等的不同，均会使土的变形发生变化，从而导致计算的变形参数产生相应的改变，理论计算结果与现场实测发生差异。这样，即使是最接近实际的三维变形状态并考虑土体固结过程中的侧向变形时，理论计算的沉降值也必须用沉降计算经验系数Ψs进行修正，这些变形计算参数可通过室内或现场试验的方法确定。

3 不同应力环境下变形计算

3.1变形计算指标和深度确定

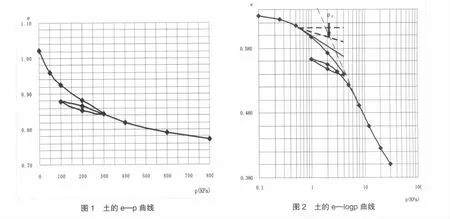
在进行地基沉降计算之前，首先要通过勘探和原位试验或室内压缩试验，测定有关计算沉降的参数。试样无侧向变形的固结试验结果，可用压缩曲线e—p（图1）或e—logp（图2）来表示，并得出反映土压缩性高低的两个指标，由公式（1）计算压缩系数av和公式（2）求得压缩指数Cc。

同时为了研究土的回弹特性，亦可进行压缩—回弹试验，得出土的回弹、再压缩曲线。

压缩系数是变量，它随压力增量的增大而减小。一般情况按 p1为 100kPa，p2为 200kPa时相对应的压缩系数a1-2值的大小划分土的压缩性。而压缩指数在较高压力范围内基本为常量。

在进行地基变形计算时，先要确定地基的沉降计算深度。沉降计算的深度，理论上要计算到无限深，工程上因附加应力扩散随深度而减小，故计算至一定深度zn（即受压层）即可。在受压层以下的土层附加应力很小，所产生的沉降量可以忽略不计。但若受压层以下尚有软弱土层时，则应计算到软弱土层底部。受压层深度zn由自重应力分布和附加应力分布两条曲线可以找到某一深度处附加应力pz为自重应力pcz的20%，此深度称为地基受压层深度zn。一般取pz=0.2pcz，但是对于软土一般取pz=0.1pcz。

3.2分层总和法和规范法变形计算

目前工程中广泛采用的变形计算方法主要有分层总和法以及规范法等。它们都是建立在地基简单分层的基础之上的。变形计算方法按照压缩曲线所取坐标的不同，又可分为e-p曲线法和e-logp曲线法。先介绍e-p曲线法。

3.2.1分层总和法

根据试验求得各土层的压缩模量和压缩系数，由下列任一公式计算第i分层的压缩量Si：

式中：pzi——第i分层土的平均附加应力（kPa）；

Esi——第i分层土的压缩模量（MPa）；

hi——第i分层土的厚度（m）；

av——第i分层土的压缩系数（MPa-1）；

e0——第i分层土压缩前的孔隙比；

e1——第i分层土压缩后的孔隙比。

地基土的最终沉降量是受压层深度zn范围内各分层压缩量之和：

3.2.2规范法

规范法主要是引入一个沉降计算经验系数ψs，计算公式如下：

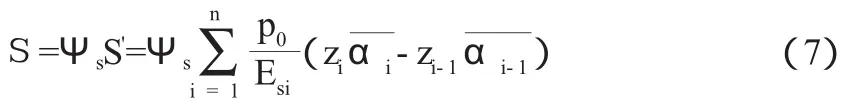
式中：S——规范法计算的地基最终沉降量（mm）；

S'——分层总和法计算的地基沉降量（mm）；

Ψs——沉降计算经验系数，根据地区沉降观测资料及经验确定，也可查文献中的表来确定；

P0——对应于荷载标准值时的基础底面处的附加压力（kPa）；

zi、zi-1——基础底面至第i层土、第i-1层土底面的距离（m）；

在计算过程中首先要根据建筑物基础的尺寸，判别在计算基底压力和地基中附加应力时是属于空间问题还是平面问题，再按荷载性质求出基底压力p0的大小和分布。然后求出计算点垂线上各分层的竖向附加应力pzi，并绘出它的分布曲线。按算术平均计算出各分层的平均自重应力pczi和平均附加应力pzi进行累加，在e—p曲线中查出相应的初始孔隙比e1和压缩稳定后孔隙比e2，从而计算出各分层压缩量Si，并进行累加后得出地基的最终沉降量S，必须注意自重应力pczi应从原地面高程算起，附加应力pzi应从基底高程算起，同时在三维变形状态下，斯肯普登—贝伦建议将分层总和法计算的沉降值S乘以一个系数Cp，即修正固结沉降S'＝Cp·S。规范法本身就是在分层总和法的基础上将计算所得的沉降值S'乘以一个沉降计算经验系数Ψs，这样才能比较准确估算地基沉降量，一般来讲软粘土地基的沉降计算值偏小，而硬粘土的沉降计算值又偏大较多。

按e—logp曲线法来计算地基的沉降与e—p曲线一样，每一分层压缩量计算同公式（5），与前述利用e—p曲线或压缩系数av计算的方法步骤基本相同，所不同的只是选用压缩性指标和确定初始及最终孔隙比的手段不同，须由对数压缩曲线求得。经推导可得出用e—logp曲线或压缩指数Cc的沉降计算公式为：

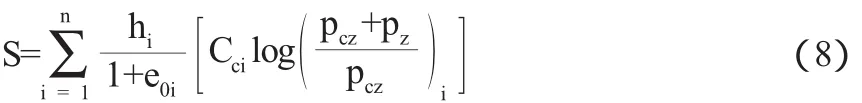
3.3考虑应力历史时变形计算

应力历史表示土在形成的地质年代中经受应力变化的情况。由于土的应力历史对土的压缩性能有较大影响，应先知道土的受荷历史，确定先期固结应力pc，才能准确计算未来在建筑物荷载作用下，地基土可能产生的新的压缩变形。根据卡萨格兰德提出的依据室内压缩曲线特征的经验图解法（图2），可在e-logp曲线上得出先期固结压力pc，用超固结比OCR＝pc/pcz来反映土体固结程度，当OCR＝1时为正常固结土，OCR>1时为超固结土，OCR<1时为欠固结土。

确定了土的固结性质，并分别确定正常固结土、欠固结土和超固结土的压缩曲线。经过大量研究者的证实，无论土受何等程度的扰动，在室内进行压缩试验时，所得的多条e-logp曲线在0.42e0处附近都趋于一点。

在超固结土中由室内的回弹再压曲线可知在曲线中存在一个滞后环，其斜率应为超固结土的超固结段压缩量的回弹指数Cs，超固结土在附加应力pz作用下地基土的沉降就由超固结段的压缩量S1和正常固结段的压缩量S2两部分总和而成。其计算公式为：

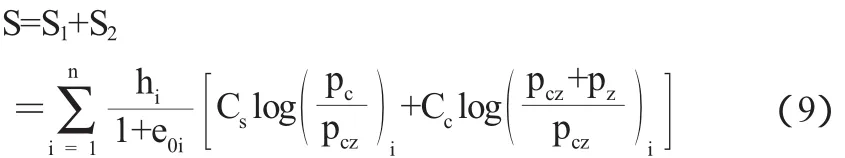
当pz较小，pz＋pcz≤pc时，则土始终处于超固结状态，此时地基土的沉降量计算公式简化为：

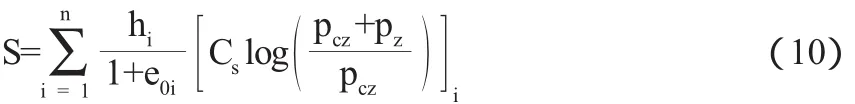
对于欠固结土，地基沉降计算公式为：

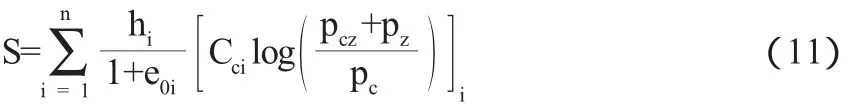
正常固结地基土的变形由前述公式（8）来计算。

3.4初始沉降和次固结沉降的计算

前面所说的地基土变形计算采用的参数都是室内固结试验得到的，时间历程较短。地基的最终变形包括初始沉降（瞬时沉降）、主固结沉降、次固结沉降，对于普通粘性土，主固结沉降是其地基沉降的一个主要部分，它对基础宽大、而压缩土层较薄，排水条件又较符合假定时较为适用。但是实际地基的地质条件往往较为复杂，有时可压缩的软土层分布较厚或土层分布不均，基底面又不是排水面，对较软的粘性土来说，次固结沉降在总沉降中占有一定比例，这时初始沉降就不可忽视；而在砂性土地基中，由于固结排水速率很快，初始沉降与主固结沉降这两部分已融合一起难以区分，这些都必须计算初始沉降或次固结沉降。

3.4.1初始沉降

对正常固结粘性土的初始沉降量Sd可按最终沉降量的15%左右估算。还可按下式计算：

式中p——基底压力（kPa）；

B——基础宽度（m）；

μ——土的泊松比；

cd——考虑基础形状和计算沉降点位置的系数，可查有关规范或手册；

E——土的不排水变形模量（弹性模量）。

3.4.2次固结沉降

次固结沉降是指在恒定的有效应力作用下地基土产生的随时间而变化的沉降。在大多情况下相对主固结沉降来说，次固结沉降是很小的，可以不计；但对极软弱的粘性土或淤泥时，或当深厚的高压缩性土层受较小的应力增量比作用时，次固结沉降则成为总沉降量的一个重要组成部分。次固结压缩系数Ca可由室内压缩试验求出，按半对数作图，当主固结完成后，次固结压缩值与时间之间的关系近似为一直线。由次固结引起的沉降量St按下式计算：

式中：tsc——包括次固结在内的整个计算时间；

tp——主固结完成的时间；

H——可压缩层的原始厚度（m）。

此外除了上述几种计算方法外，还有通过室内试验模拟现场应力路径，再量取土样的垂直变形的应力路径法等。

在工程设计中，不但需要预估建筑物地基可能产生的最终沉降量或沉降差，而且还常常需要预估基础达到最终沉降量所需的时间或者预估建筑物完工以后经过某一段时间可能产生的沉降量，即基础的沉降量与时间关系的问题。目前多以饱和土体单向固结理论（一维固结理论）为基础进行求解，随着理论研究的深入，还有二维、三维固结理论，它更符合地基土体的受力和变形情况，但计算公式非常繁杂。

3.5几种方法沉降计算结果比较

表1是作者收集到的不同计算方法所得变形值与实测沉降量比较。

由于地基土性质变化的复杂性，采取原状土样的困难，边界条件及加荷情况与计算时所采取的简化情况有所差异，以上各种变形计算的方法计算结果往往与实测沉降有一定的差别。

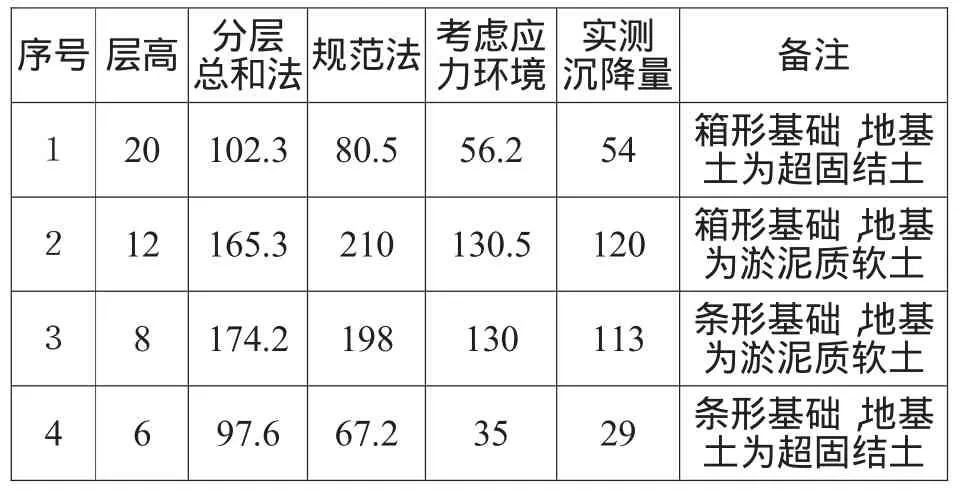
表1 计算沉降量与实测沉降量的比较

从表1中可以看出，如果不考虑地基土应力环境，计算的变形量与实测值差别很大，考虑了地基土的应力环境，计算值虽然与实测值有差别，但非常接近。

4 结语

在建筑地基基础设计中，变形计算是一个很重要的环节。由于地基土的沉积环境变化很大，性质根本不同，边界条件及加荷情况也不一样，很难用某一种方法来计算不同地基土的变形，而要根据其特点选用适合该建筑物的计算方法，才能比较准确地计算其沉降量。

变形计算参数的取得方法也影响到其计算结果，目前大多采用一维固结试验取得压缩系数、压缩模量、回弹指数等，随着试验技术不断改进，采用真三轴仪进行竖向应变测定，可直接用于沉降计算。另外在计算技术上，近似解法已有较好的应用，特别是利用电子计算机按有限元理论进行求解。目前水利工程中，对于各类建筑物的容许沉降量与沉降差尚无统一标准可循，因此要加强沉降的实地观测以及观测资料的积累，并与理论计算值相比较，从而推动理论的改进，给设计提供可靠的依据■