基于改进凸包算法的移动端条码图像定位与校正

鲁 剑,刘 志

(浙江工业大学 软件学院,浙江 杭州 310032)

Data Matrix条码属于矩阵式二维条码,其尺寸与编入资料量相互独立,最小尺寸达到所有条码之最,由此特别适合标识小物品;同时它采用 Reed-Solomon交织交叉编码,编码时加入纠错码,最少只需读取20%图像信息,即使大面积受损仍不影响准确识别.

Data Matrix条码是由黑白相间的小方格(模块)组成的正方形或长方形.Data Matrix符号由排列规则的正方形模块组构成的资料区组成,资料区的四周由定位图形(Finder Pattern)所包围,定位图形的四周再由空白区包围.定位图形是资料区域的一个周界,为一个模组宽度.其中两条“L”形邻边为暗实线,主要用于限定物理尺寸、定位和符号失真.另两条邻边由交替的黑色和白色模块(Module)组成,主要用于限定符号的单元结构,但也能帮助确定物理尺寸及失真[1].Data Matrix以资料区中的模块来表示信息,每个模块代表一个位信息0或1,其中黑色模块代表1,白色信息代表0.Data Matrix可编码字元集包括全部的ASCII字元及扩充ASCII字元,可表示字母、汉字、图像等信息.Data Matrix条码最大可以容纳3 116个数字信息,2 335个文字数字信息,1 556个位信息.

1 移动端基于改进凸包的条码图像定位

1.1 凸包相关内容

1.1.1 上、下凸包

所谓的上凸包(upper hull),就是从最左端顶点P1出发,沿着凸包顺时针行进到最右端顶点Pn之间的那段,换言之,组成上凸包的,就是从上方界定凸包的那些边,此后,再自右向左进行一次扫描,计算出凸包的剩余部分——下凸包(lower hull),如图1所示.

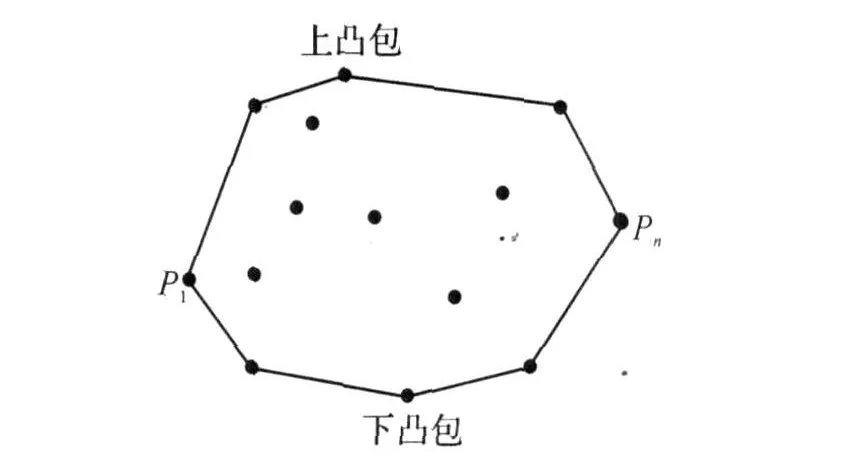
图1 上、下凸包Fig.1 Right turn

1.1.2 右拐

对三个点进行比较,判断它们是构成左拐还是右拐的时候,有可能它们恰好共线.在这种情况下,居中的那些点不应该出现在最后的凸包上,因此只有在三个点的确构成一个右拐的时候本文才认可为右拐[2],如图 2所示.

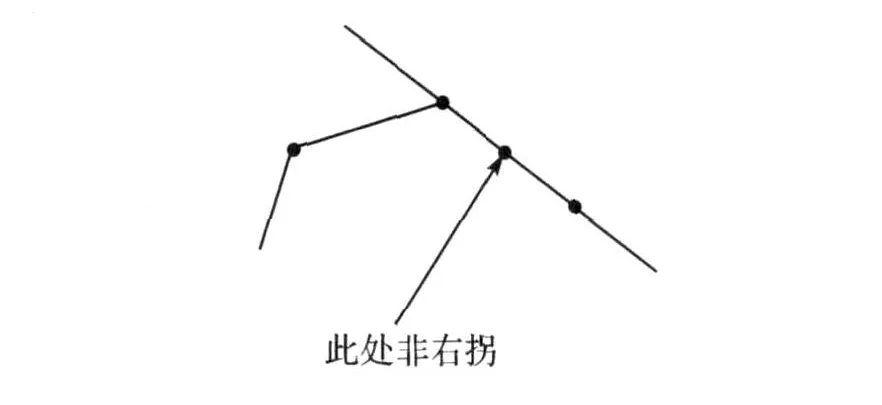
图2 右拐Fig.2 Upper and lower hull

1.2 凸包检测前的点集简化处理

针对手机端实时性要求和硬件限制[3],通过手机摄像头捕获的初始二维条码图像(图3),经加权平均法灰度化,快速自适应阈值Otsu法二值化(图4),然后经Sobel算子分别用水平和垂直检测模板图像进行卷积,边缘检测效果见图5.

智能手机(Smart phone)相比传统PC普遍存在主频不高、内存有限等问题[4],由此筛选边缘检测后的条码像素点,只提取黑色像素点加入凸包检测点集,减轻运算量.

由于凸包内部点集显然不可能成为最后的凸包顶点,并且这部分往往数目巨大,剔除内部点集可以大大减少后续计算量,提高手机处理效率.

首先引入叉乘:两个向量进行叉乘得到的是一个向量,方向垂直于这两个向量构成的平面,大小等于这两个向量组成的平行四边形的面积,因此对任何三点构成的两个向量取模后再取1/2即得到由此三角形面积.

(1)在经边缘检测后的二维条码图像上不难找到如下四个最值点:最左端点,最右端点,最顶端点,最底端点,分别记为 minPx,maxP x,minPy,maxPy.

(2)任何一点P与此四最值点构成的四个三角形面积之和如果等于四最值点构成的四边形面积,那么点P位于四边形内部或者在四边形边上,否则点P位于四边形之外.

(3)通过此方法我们去除最值四边形内部点和边点集,将四个最值点和界外剩余点加入点集进行凸包检测.

通过叉乘方式删除这部分非凸包顶点序列,可以大大减少进行凸包运算的点集数目.如图6所示,由a,b,c,d四边所构成的四边形上以及其内部点将被删除,进行凸包运算只有四边形外的点集以及四边形四顶点,这部分点集数目相对不处理前大为缩减.

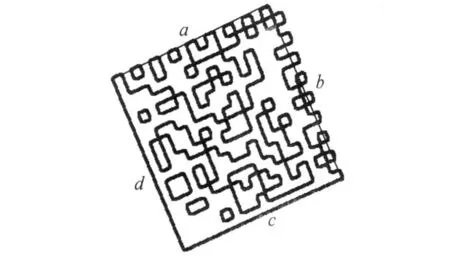
图6 删除内部和边上的点集Fig.6 Delete interior and edge points

1.3 Graham凸包顶点检测

为避免实际二维条码图像可能存在的毛刺等问题,使用字典序排列点集,即不仅仅根据各点的x坐标来确定先后次序,首先按照x坐标排序;如果存在多个x坐标相同点,进而按照y坐标为它们排序 .

凸包算法通常分为增量方法(incremental method)、包裹法(Jarvis march)及分治法(divide-and-conquer method)等,这里采用Graham扫描法(Graham's scan),其应用“旋转扫除”(rotational sweep)技术,通过判断各个顶点相对参照顶点的极角值大小依次处理,Graham扫描法运行时间为O(nlgn).

经过上述步骤简化处理的条码图像,设其点集序列为p1,p2,… ,pn.

(1)将最左端点p1及其邻点p2加入lupper.

(2)把p3,… ,pn逐个加入lupper,通过判断末尾三点末是否构成右拐的方式得到上凸包点集lupper.

(3)采用相似方法从相反方向扫描点集,得到下凸包点集llow er,将其与上凸包合并,去除重复,得到凸包顶点序列∑(P).

1.4 精简凸包顶点

标准Data Matrix条码图像经过凸包检测必将得到5个凸包顶点,但是对于实际条码图像来讲情况并非如此,图6经过凸包检测后的顶点集中就存在22个顶点,其原因为实际条码图像很难达到标准图的精准程度,5个顶点周边存在干扰点的现象以及边框上存在凸起像素点的现象不在少数,去除这些干扰点可以大大提高条码定位精准度.

对于凸包顶点集∑(P)中任何一点Pi,分别找到其相邻两点,记为last和next,其本身设为current(图7).通过计算斜率值并由反三角函数分别得到相邻两边的角度值,记为t1和t2,如若两角度差值|t1-t2|小于某一阈值,则可将三点认为近似共线.经统计分析,得到阈值 13,记为 minimunDifference.同时得到current,next两点之间的距离,记为sideLength.如若同时满足条件:角度差值|t1-t2|＜minimunDifference以及sideLength＜10,阈值10为经统计分析所得,则排除该点.由此排除实际条码图像顶点附近存在的干扰点以及各条边上存在的凸起像素点.

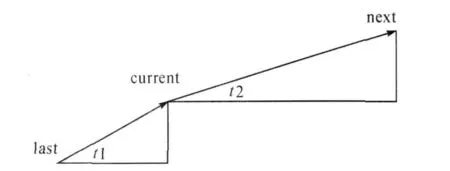
图7 通过角度筛选凸包顶点Fig.7 Delete points through angle

1.5 拟合条码图像

(1)得到二维条码图像的凸包顶点序列后,依次连接Pi,Pi+1点,首尾相接形成多边形.

(2)计算Pi,Pi+1所成边的边长,保留长度值最大的四条边记为edge0,edge1,edge2,edge3.

(3)依次将四条边edge0,edge1,edge2,edge3与其余各边相交得交点(intersaction),排除重复交点,最终得到伪四边形(Fake quadrilateral)的四个顶点(图8).

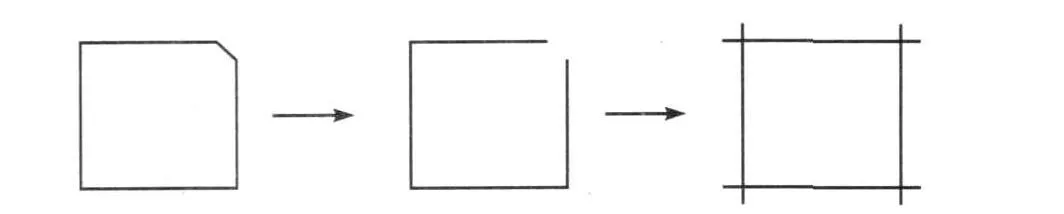
图8 “伪四边形”形成过程Fig.8 The procedure of“Fake quadrilateral” creation

图3经上述处理后,其拟合四边形的四个顶点分别为P1(0,75),P2(85,231),P3(232,164),P4(171,2),拟合的“伪四边形”如图9所示.

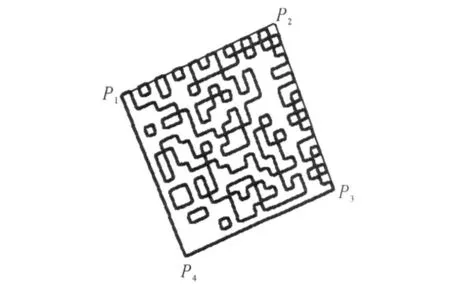
图9 原始图像的拟合四边形Fig.9 Fake quadrilateral of original image

2 条码图像畸变矫正

2.1 几何校正模型

二维条码图像在经手机摄像头或扫描系统获取过程中都可能发生畸变,尤其是轻微畸变在所难免,由此导致几何失真.广泛采用的几何坐标校正模型包括:双线性模型、多项式模型和三次卷积模型等[5].三次卷积模型虽然具有较高精准度,但其计算量巨大,运算效率低,很难适应移动端运行环境,同时也不能满足系统实时性要求.一般情况下,条码图象发生的畸变属于双线性范畴,故笔者采用双线性模型.f(x,y)表示校正后的无失真图象,g(x′,y′)表示待校正的畸变图象;f(x,y)=g(x′,y′),即:点(x,y)经过畸变坐标值变为(x′,y′):

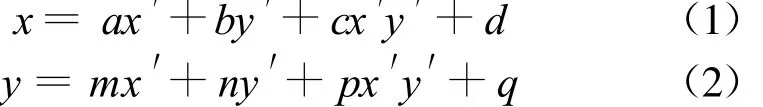
2.2 条码图像几何校正

针对移动端屏幕尺寸特征,通过设置200×200正方形区域,条码内各像素点映射其中即完成畸变校正(图10).

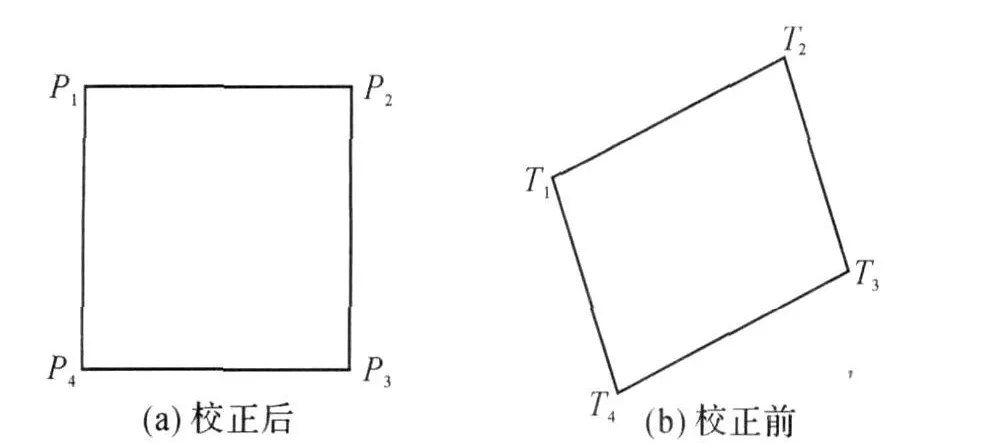
图10 条码控制点变换图Fig.10 Position changing of the control points

首先取条码图象“伪四边形”四顶点作为控制点 ,设 T1,T2,T3,T4 的坐标分别为(x′1,y′1),(x′2,y′2),(x′3,y′3),(x′4,y′4);P1,P2,P3,P4的坐标分别为(x1,y1),(x2,y2),(x3,y3),(x4,y4);则由式(1,2)可得到x,y,x′,y′的双线性方程组:

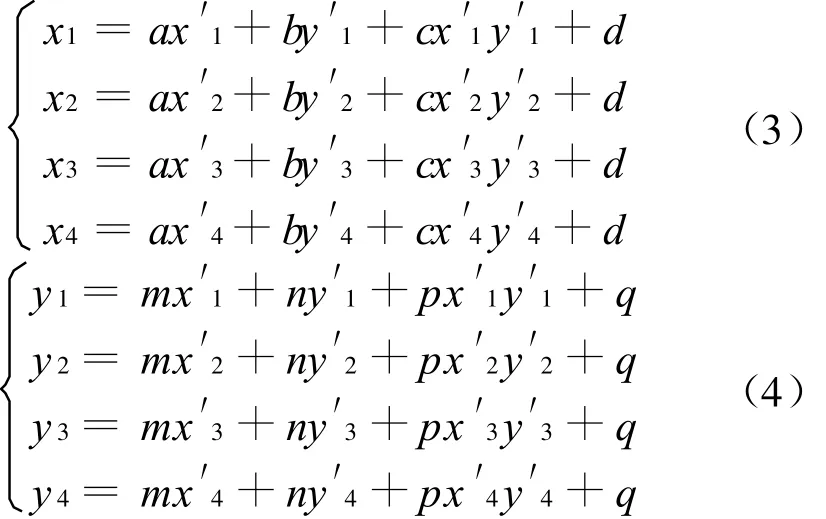
由于校正前后8控制点P1,P2,P3,P4,T1,T2,T3,T4为已知,通过双线性方程式(3,4)即可确定双线性映射的映射系数.因此通过以上映射系数,校正图像中的任意一点(x,y)的灰度值 f(x,y)都可由对应的畸变点(x′,y′)的灰度值 g(x′,y′)得到.

2.3 像素点灰度值校正

由于输入图像只在整数位置定义灰度值,变换后的输出图像中与其对应的点坐标值并不能确保为整数,即空间变换后的点不可能总是落在实际图像的像素点上,所以实际图像上各点的灰度值是根据附近各像素点的灰度值得到.

常用的灰度插值算法包括最近邻插值、双线性插值及高阶插值等.最近邻插值简单地通过取浮点坐标最邻近的像素点得到对应的灰度值,校正后的图像亮度有明显的不连续性;双线性插值法是利用四相邻点的灰度在纵横双向做线性内插,所以其算法产生的图像质量较好,不存在灰度不连续的情况.

对条码图象的灰度计算采用双线性插值(Bilinear interpolation approach)校正法恢复,根据点所在的单元正方形4个顶点坐标来计算其灰度值(图11).

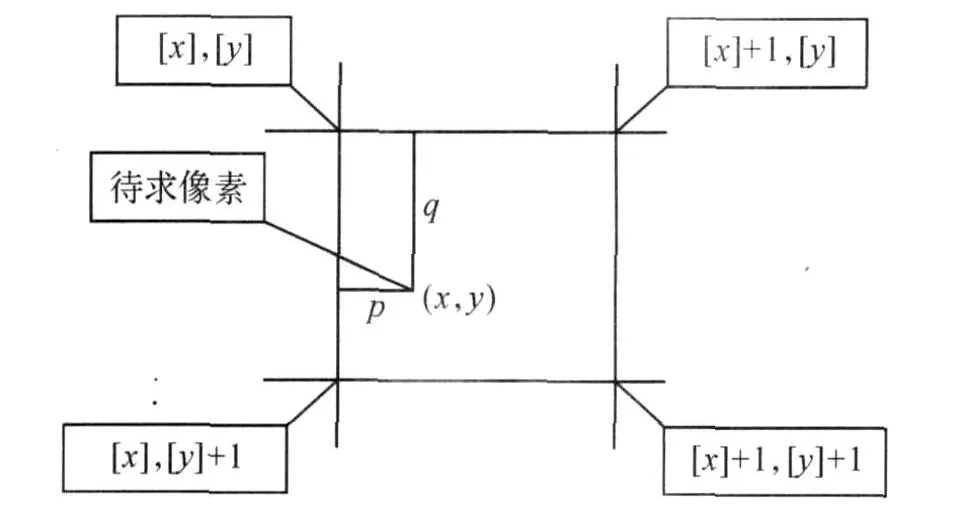
图11 双线性插值示意图Fig.11 Bilinear interpolation approach

d(x,y)=(1-q){(1-p)×d([x],[y])+p×d([x]+1,y)}+q{(1-p)×d([x],[y]+1)+p×d([x]+1,[y]+1)},d(x,y)表示坐标(x,y)处的灰度值,[x],[y]分别为不超过x和 y的整数值.二值化后的条码图象,经畸变校正后的结果如图12所示.

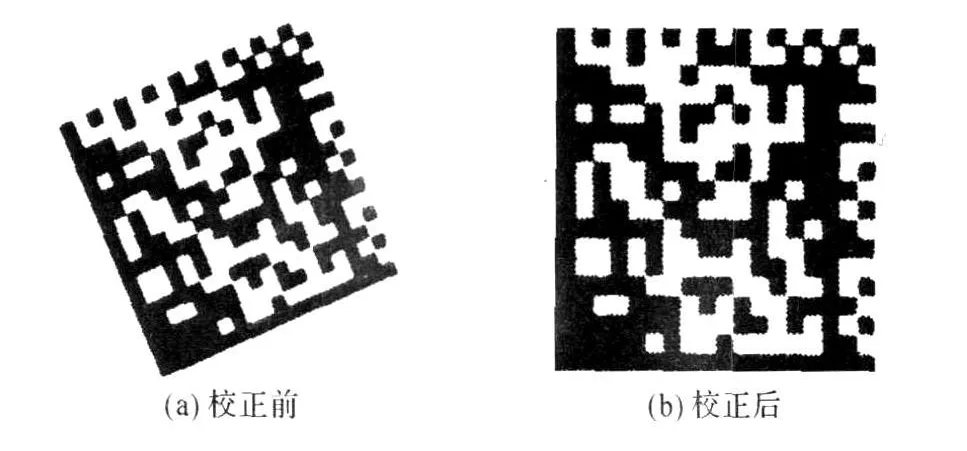
图12 校正前后的条码二值化图像Fig.12 Images before and after correction

3 实验结果

测试所用手机为Nokia N73,其硬件配置:ARM 9 CPU,处理器的时脉(Clock Rate)220 MHz;64 MB内存,软件环境:Symbian OS 9.1 Series 60 3rd Edition.

图13为二维条码图像经过自适应阈值分割后的二值图像,在手机端经过Sobel算子边缘检测后分别进行Hough直线检测[6]和改进凸包定位及校正的效果图.实验中调用自编写的由无穷级数近似的三角函数,其运行时间对照如表1所示.

图13 文中算法与传统算法实验效果Fig.13 Results for the two methods

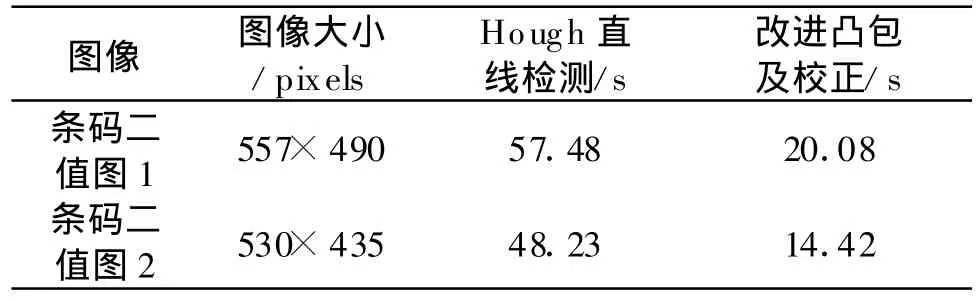
表1 笔者算法与传统算法处理时间对比Table 1 Time compare between two algorithms

4 结 论

通过预处理以差乘方式排除大量内部无效点集,采用算法复杂度为O(nlgn)的Graham扫描法得到凸包顶点集,最后通过角度、长度等方式准确筛选凸包顶点减少计算量,提高效率.实验表明:笔者方法对实际Data Matrix二维条码图像的定位和校正效果明显,并且适应手机端软硬件环境,但是对于畸变幅度较大的条码定位和校正处理效果并非很理想,有待进一步提高.

[1] International Organization for Standardization.ISO/IEC16022-2000 Information technology-international symbology specification-data matrix[S].Switzerland:ISO,2004.

[2] 潘金贵,顾铁成.算法导论[M].北京:机械工业出版社,2006.

[3] 杨常青,彭木根.Sy mbian S60手机程序开发与实用教程机械工业出版社[M].3版.北京:机械工业出版社,2008.

[4] EDW ARDS L,BARKER R.Developing series 60 applications[M].北京:人民邮电出版社,2005.

[5] 蔡文婷.移动端二维条码图像增强及应用研究[D].杭州:浙江工业大学,2008.

[6] 陈媛媛,施鹏飞.二维条形码的识别及应用[J].测控技术,2006,25(12):17-19.