润滑和污染对轴承寿命的影响(一)
润滑和污染对轴承寿命的影响(一)
轴承寿命受许多因素影响,两个最重要的因素是润滑和污染。通过更好地认识这些因素是如何导致轴承寿命缩短的机理,我们就能改善轴承设计和运行。本文是两个部分的系列之一,首先研究润滑的影响。
机器设备使用滚动轴承的优点十分明显,它能减少摩擦损失,提高系统的整体效率。但这需要充分降低疲劳失效带来的风险。滚动轴承利用了滚动接触的集中特性 (赫茨接触)来承载负荷,这就产生了很高的局部压力和应力,因此需要良好的润滑和接触表面,来避免进一步的应力集中。
轴承滚道上出现的表面粗糙、颗粒凹痕和污染痕迹都会导致应力集中,加快表面引起的疲劳。在凹痕上形成的润滑膜,以及相关的局部表面应力,也是诱发裂缝的重要因素。本文提出了一种新方法,将微流体弹性动力润滑膜 (微EHL)和相关的局部应力与滚动轴承的疲劳寿命联系了起来,请参见 [1]。这个应用方法是对表面微几何形状 (包括凹陷)的谐波成分做傅里叶分析,来预测流体力学压力、应力、以及产生的润滑膜。本文讨论和分析了这种方法在实际轴承表面的应用,并涉及了一些现有的微接触EHL解决方案。最后用滚动轴承寿命评定中所用的润滑质量系数ηb作为关联因素。在本文的第二部分,讨论了污染和表面凹陷,以及它们与第一部分中介绍的微EHL模型的关系等问题。
1.轴承寿命评定中的微几何形状影响
根据Ioannides等人[2]的研究,计算滚动轴承寿命的公式为:

在式 (1)中,应力寿命修正系数askf(定义见[2])为下面的形式:

askf中的惩罚因子0≤η≤1是除完全理想光滑的赫茨应力外,对滚动接触表面的实际应力基于平均考虑。对η因子的分析评定,需要量化轴承运转中滚动接触面出现的真实应力状况。而滚动接触面的实际应力状况,可能是许多局部的宏观和微观表面特征相互作用的结果。这与表面分离的程度有关,例如润滑状况以及接触面的颗粒污染。根据 [3],轴承润滑状况的一个简单评定参数就是粘度比κ。[4]详细解释了这个工程润滑参数的推导过程。κ参数的定义是轴承在工作温度下的实际润滑剂粘度 (v)与足够润滑该轴承的标准参考粘度 (v1)的比值[5,6]。
根据 [6],润滑参数κ也可与滚动接触面的具体油膜厚度Λ相关,两者近似关系为:κ≈Λ1.3。
按照 [2],公式 (2)中的惩罚因子0≤η≤1可以描述为两个同时产生的量—润滑系数ηb和污染系数ηc—的乘积:
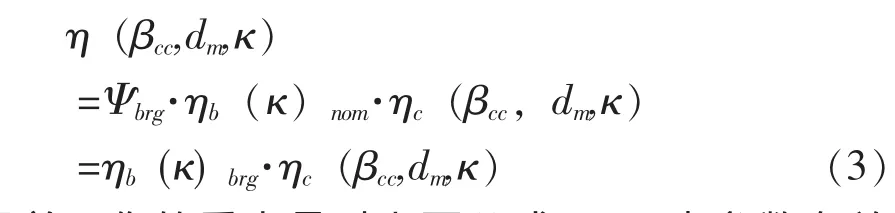
目前工作的重点是对上面公式 (3)中参数有关的表面和表面下应力条件进行量化 (包含EHL润滑膜),以便能提供分析轴承动态评定中使用的惩罚因子η的手段。
许多研究者曾使用解析、半解析和数值方法,研究了在整个赫茨接触面上的凹痕、粗糙或其它缺陷等几何形状特点所引起的表面应力。[7]介绍了一个早期的全数值解决方案,它考虑了滚动接触面上的简单凹痕或突起物的EHL接触问题。
最近出现了一个基于使用FFT(快速傅里叶变换)的快速技术,用来计算EHL压力,以及由粗糙或凹痕等微几何形状所引起的相关表面应力[8,9]。这种方法特别适用那些需要分析实际的粗糙和凹痕对润滑膜的形成和相关EHL的影响。这种方法提供了一种强大的新工具,能用来解决微EHL问题和相关的实际轴承接触的表面应力。
在这个新方法中,介绍了单弦粗波 (或许多波的合成)的微EHL特点。通过使用上面的方法,可以计算完全瞬时条件下的弹性变形和相关的压力波。然后就可以应用单弦粗波,以及由此引起的在赫茨接触面内的变形和压力的解法 (因为在高压区,雷诺方程可以简化成线性形式)。也可以把傅里叶分析应用到波频率的全区间,形成滚道的微几何形状。请注意还有一种不同的技术,也是基于傅里叶分析,也可以用来计算表面下应力[9]。组合使用这些表面和表面下应力的数值计算技术,提供了快速分析实际轴承表面状况的强有力工具。因此可以评估在不同的润滑条件下,实际滚动轴承滚道的表面和表面下应力。
2.微几何形状压力和应力模型
传统上,数值解法一直用于EHL和微EHL的建模(解决微几何形状),这样用钢的弹性方程和润滑剂状态方程 (压粘度和压缩性)就能替代求解流体的雷诺方程,例如 [10]。在这些表面中某个表面的微几何形状和粗糙因为雷诺方程中挤压效应的影响,在解法中意味着效应是与时间相关的,对线接触为:
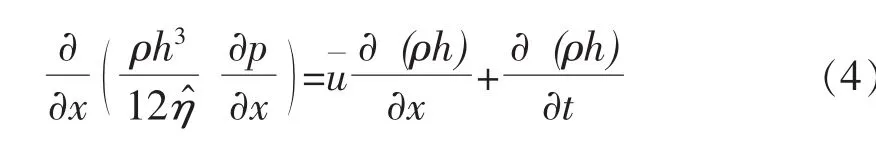
这个分析来自 [8]。在EHL接触中,压力如此之高,润滑剂变成近乎固体,这样→∞,雷诺方程可以线性化为:
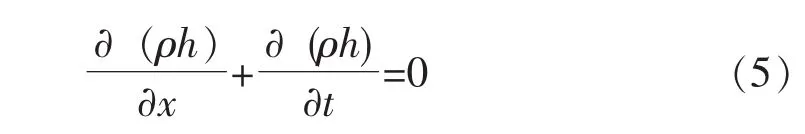
这个方程可以用于在纯滚动中进入EHL接触的低振幅单弦粗波。在这种情况下,方程就相当于波传输方程,因而可以找到局部压力和油膜厚度的解析解法,例如 [11,8]。更重要的是,由于这个方程是线性的,因此可以用强大的傅里叶技术 (FFT和IFFT)来解决复杂的表面几何形状。用这种方式就能在赫茨接触的中心获得粗糙样本的微EHL压力和变形。
一旦获得EHL压力,就能计算表面下应力。应力符合线性弹性材料 (钢)的特点,所以使用了也是基于傅里叶方法的另一种技术,详见 [9]。这样,每个正弦压力和来自库仑摩擦的相关表面张力等所有应力分量都可以计算出来。因此,这个方法是计算每个压力和张力正弦分量的应力分量,然后再组合成完整的应力。
2.1微EHL解析的结果
下面用一个理想化的凹痕 (正弦形状但没有肩)为例,来为凹痕建模。在这个例子中,滚动轴承以各种不同的滑动/滚动比通过EHL接触面,接触和润滑条件都是典型状况。
在图1所示的条件和凹痕几何形状 (但没有肩)下,最大范米斯应力为0.34po。我们基于目前的FFT方法做了一个仿真,使用同样的条件,但是凹痕几何形状更为现实,即凹痕全周都有0.15μm高的肩(如同颗粒的弹塑性凹陷)。由于现有技术只能处理压力和间隙波动,光滑EHL压力近似于赫茨压力分布,所以把它加入了。图1显示当凹痕在接触面中心时,无因次压力 (相对最大赫兹压力规格化)和间隙 (相对中心光滑油膜厚度规格化)的计算结果。

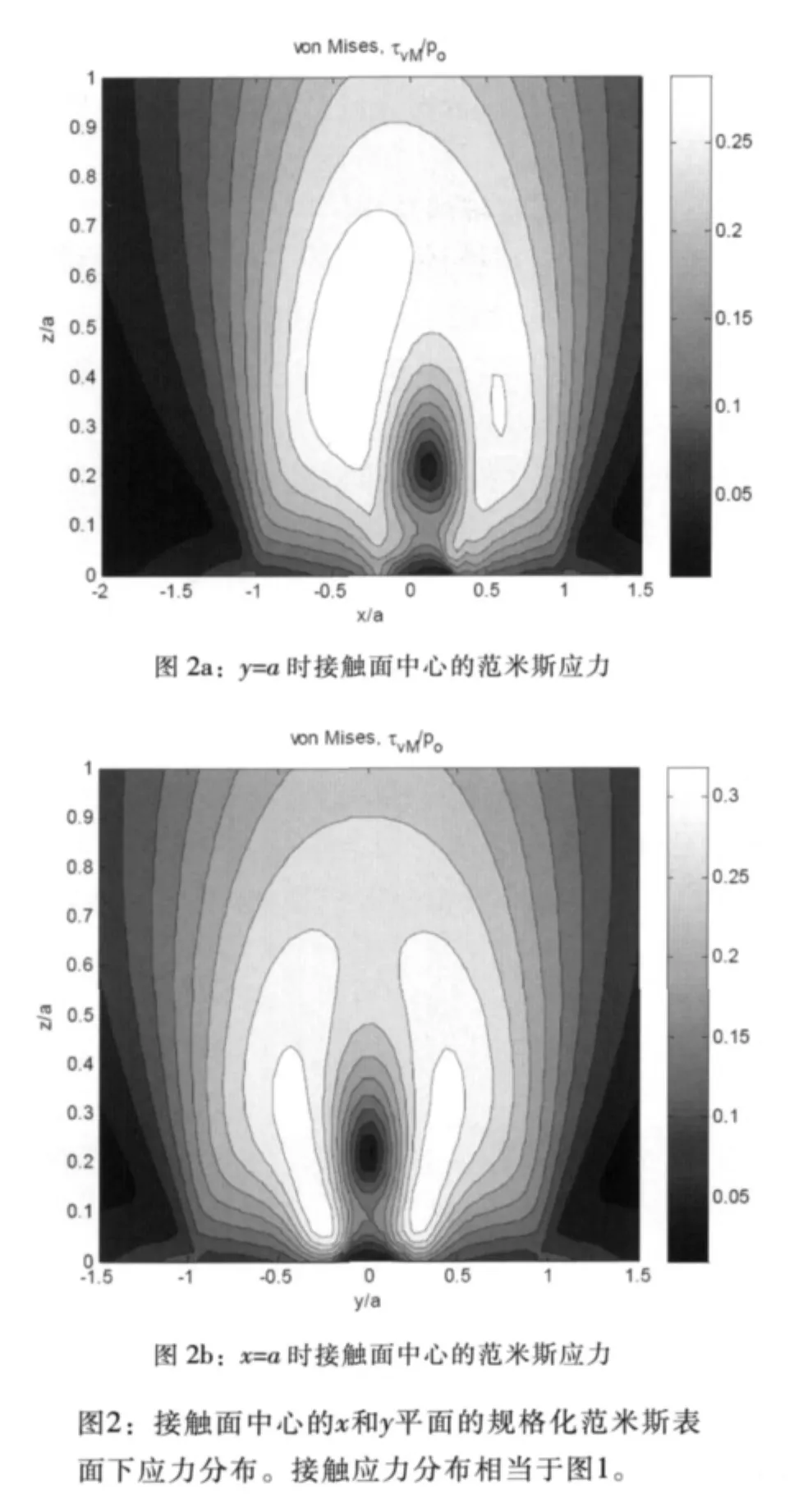
图2显示,在接触面中心的两个平面 (y=0和x=0)的范米斯应力场 (相对最大赫兹压力规格化)相当于图1中的压力分布。出于更现实的考虑,在凹痕边缘安排肩,这种情况下计算的最大范米斯应力为0.42po,比没有肩的情况下上升23%。
2.2用微EHL分析轴承表面粗糙
目前的微EHL模型也可以用于实际轴承表面粗糙,下节介绍用光学廓线仪绘制3D轴承滚道外形的示意过程,图3列出了用微EHL分析获得的典型样本结果。

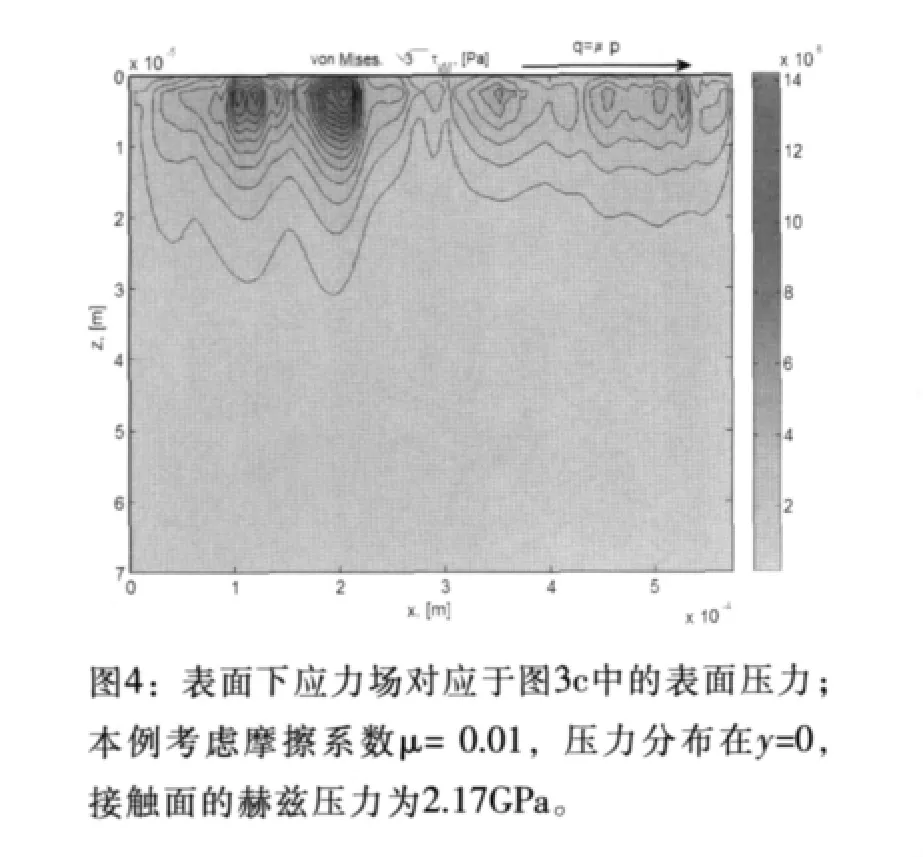
在图3a中,结合润滑接触面的运行条件,使用了一个轴承外形样本,来计算弹性变形外形 (图3b)和相关的微EHL压力波动 (图3c)。图4显示了滚动方向上相关的范米斯表面下应力场,清楚说明了粗糙微接触引起的微表面下应力集中。
图5展示了第二个例子 (不同的油膜厚度)。在这个例子中,因油膜厚度减少大约34%,最大压力升高30%。
可以看到,利用目前的方法,较薄的润滑剂膜(低)倾向于产生压力波动,这越来越与干接触条件下的情况相类似。较厚的油膜会显著抑制压力波动的发展,减少表面不平的压力状况,减轻滚道的微接触疲劳。
下一节将用微EHL模型来评估粗糙度和润滑对轴承寿命的影响。
3.与润滑质量系数的关联
下面讨论以粘度比κ为代表的润滑质量,与相应的轴承寿命下降和疲劳载荷极限之间的理论关系。为此需要量化实际滚动轴承的疲劳寿命下降,要用标准表面粗糙度与理想光滑滚道的粗糙度相比,所谓理想滚道就是无摩擦纯赫茨应力分布的假设。这可以用比较实际轴承 (有标准粗糙度)的理论疲劳寿命和具有理想光滑和无摩擦表面的假设轴承的疲劳寿命来获得,这样寿命比就量化为下面的形式:
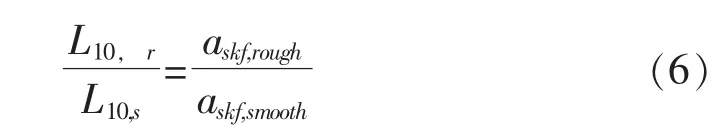
可以用作用在实际滚动接触的疲劳寿命应力积分来数值估计上面的比值:
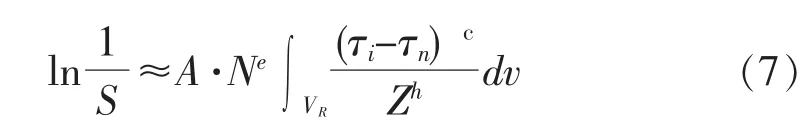
在式 (7)中,影响寿命比 (6)的相关数值,是与体积相关的应力积分,它为:
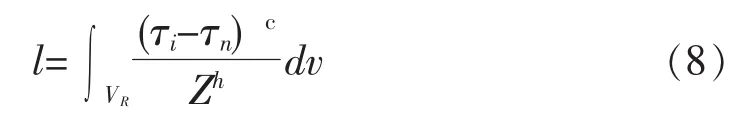
用上面的等式,寿命方程 (1)表示如下:
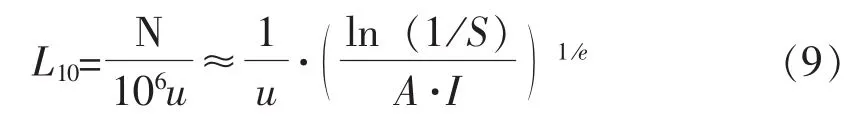
用这个公式,就能计算出标准粗糙度和理想光滑接触两者的应力积分 (I),这样在式 (6)给定寿命比后,就能用它估计对轴承寿命的影响。换句话说,下面等式成立:
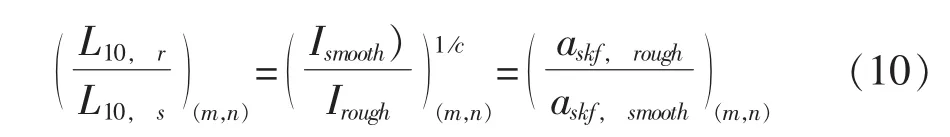
一般来讲,式 (10)比值取决于表面外形 (指数m),以及表面分离值或位于接触面中的润滑剂膜值(指数n)。
现在能通过引入式 (3)中应力寿命系数,直接从式 (10)推导出润滑系数 。在理想干净润滑剂的假设下,污染系数 可以认为不变。这样,对标准滚动轴承粗糙度,应力寿命系数可以表达为:

类似地,对具有理想光滑滚道的假设轴承,可以把ηb设为不变,应力寿命系数就变为:
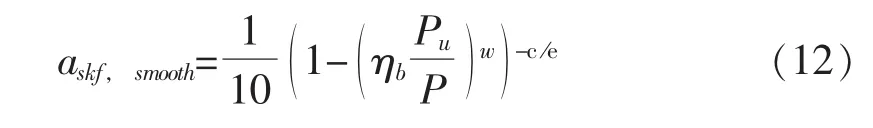
将式 (11)和式 (12)带入式 (10),得到下面的等式:

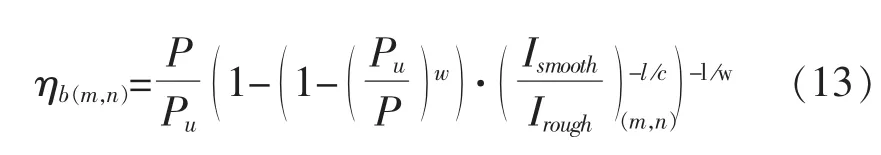
式 (13)说明,从疲劳寿命和相关的标准粗糙轴承表面的应力-体积积分开始,就能建立数值推导出来的η'b值的 (m×n) 矩阵。
必须将这个计算扩大到能包括表面分离 (油膜厚度)的不同值,从薄油膜到滚动接触的完全分离。我们把下节详细说明的计算过程应用于η'b(m,n)的数值评估,因为它是实际滚动轴承表面的代表样本。
按照上面介绍的方法, 就能获得一组η'b(m,n)值,把这些计算出的数据点和差值曲线绘在图6的κ-η'b图表中。为了能清楚说明,只列出了典型轴承表面的一组代表数据。数值产生的η'b(κ)曲线始终显示了一种典型趋势,就是随着接触面的名义润滑条件κ的下降, η'b出现快速下降。
不同的作者[10]曾讨论过,无因次波长参数▽=(λ'/a)有可能提供更好的表面粗糙处的压力上升与ηb之间的相互关系。如果润滑参数不仅仅包括油膜厚度,还考虑了粗糙波长,就有可能为不同粗糙质地与相应的ηb提供比图6所示的更好微分。
但是,标准化动态寿命评定要求基本上确保滚动轴承性能,要有个低限,或安全极限。这样能保证在多种可能的表面粗糙质地类型下,轴承都能良好工作。因此,考虑到κ是轴承工程实践中广泛使用的润滑参数,这个简单的粘度比方法看起来是足够的,当然还很方便。关于图6中ηb(κ)曲线的总体形状,应当注意到Tallian等人[3]获得与寿命比 (Λ)曲线非常相似的结果,这说明大家实际上观察到的是同一个基本物理现象。
数值计算的一个局限性是接触面要有最小量的油膜 (以保证流体流动方程使用的连续性条件)。因此如果κ值低于~0.2,就很难估算。也可以使用纯干条件来估算疲劳应力积分,因为这种情况下可以忽略油膜。但是,如同图6中曲线的总体趋势显示的那样,ηb的趋势是趋向图的原点,接近κ值域的名义下限。
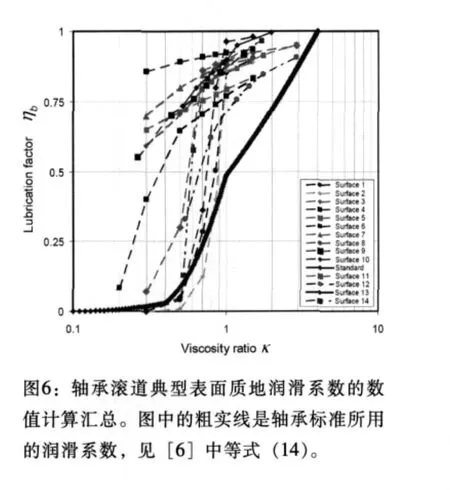
为了比较,在图6中, [2]中的润滑参数方程也可以表达为如下形式:
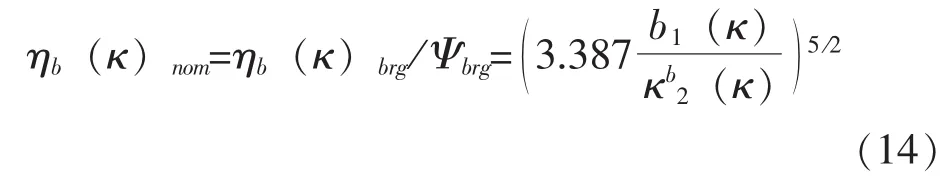
在式 (14)中,为κ值域的三个区间规定了常数b1和b2,Ψbrg也是个常数,代表四种主要滚动轴承类型的一种:径向球轴承、径向滚子轴承、推力球轴承和推力滚子轴承。在目前的评估中,我们将数值计算获得的η′b与式 (14)中的润滑系数的规格化标准形式ηb(κ)nom做了比较。图6中用粗实线标出的关系(14),相比数值计算的η′b结果,有较好的安全设置。实际上,图6显示几乎所有被分析的表面粗糙样本都远高于标准极限线。这说明对评定轴承的润滑条件和预期耐久寿命,式 (14)是个合理的、安全的选择。
数值评估中使用的一些粗糙质地来自正在做耐久试验的轴承。实验结果 (第二部分),将进一步比较耐久试验寿命和用式 (14)中润滑系数获得的寿命,第二部分还讨论了滚动轴承在各种润滑条件下的耐久试验。
总体计算方法总结在图7中,说明如下:
◎用光学显微镜测量实际轴承外形,描绘赫茨接触中心的一个点。
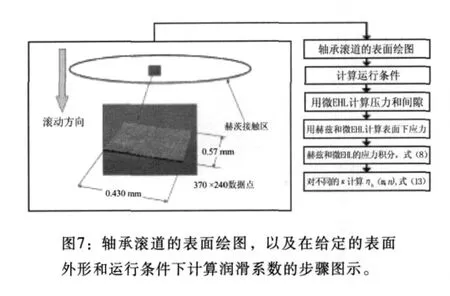
◎将测量而得的微几何形状分解为正弦分量。
◎利用接触面的运行条件,用解析解法求解每个正弦分量的压力和变形。
◎合成压力和油膜厚度结果。
◎使用微应力方法计算表面下应力。
◎ 用式 (13)计算目前例子的ηb参数。
4.讨论和结论
本文讨论了推导滚动轴承寿命评定中润滑质量系数的基本理论。这个系数可能与微EHL压力、应力和疲劳损坏有关,所以它提供了在滚动轴承寿命评定中,衡量润滑质量影响的一种手段。通过使用测量获得的不同滚动轴承外形和润滑条件,发现不同的外形对寿命评定有不同的影响。但是, [6]中提出的模型,算出的安全极限是保守的,能很好地覆盖这里分析的大部分案例。
本文提出的微EHL方法,是一种评估滚动接触中,任何低振幅外形特点 (粗糙或凹陷)的疲劳损坏影响的有效方法,避免了大量使用计算机进行数值解法。本文的第一部分使用这种方法来推导滚动轴承的润滑系数ηb,第二部分将用这种方法来推导污染系数ηc。
参考书目
[1]Gabelli,A.,Morales-Espejel,G.E.,Ioannides,E.,Particle Damage in Hertzian Contacts and LifeRatings of Rolling Bearings,Tribol.Trans.,vol.51,pp.428-445,2008.
[2]Ioannides,E.,Bergling,G.,Gabelli,A.,An Analytical Formulation for the Life Rating of olling Bearings,Acta Polytechnica Scandinavica,Mech.Eng.Series,137,1999.
[3]Tallian,T.E.,Chiu,Y.P.,van Amerongen,E.,Prediction of Traction and Micro-Geometry Effects on Rolling Contact Fatigue Life,Trans.ASME,J.of Trib.,vol.100,pp.156-166,1978.
[4]Bolton,W.K.,Elastohydrodynamic in Practice,Rolling Contact Fatigue:Performance Testing of Lubricants,Tourret,R.,and Wright,E.P.,Ed.;The Institute of Petroleum,London,pp.17-25,1977.
[5]Harris,T.A.,and Kotzalas,M.N.,Advanced Concepts of Bearing Technology,CRC Taylor&Francis,240-246,2007.
[6]International Standard:Rolling Bearings-Dynamic load rating and rating life,ISO 281:2007.
[7]Venner,C.H.,Mutilevel Solutions of the Line and Point Contact Problems,Ph.D.dissertation,University of Twente,Enschede,the Netherlands,1991.
[8]Morales-Espejel,G.E.,Lugt,P.M.,Van Kuilenburg,J.,Tripp,J.H.,Effects of Surface Micro-Geometry on the Pressures and Internal Stresses of Pure Rolling EHL Contacts,STLE Tribology Transaction Vol.46,pp.260-272,2003.
[9]Tripp,J.H.,Van Kuilenburg J.,Morales-Espejel G.E.,Lugt,P.M.,Frequency Response Functions and Rough Surface Stress Analysis,STLE Tribology Transaction Vol.46,pp.376-382,2003.
[10]Venner,C.H.,and Lubrecht,A.A.,Multi-Level Methods in Lubrication,Elsevier Science,2000.
[11]Greenwood,J.A.,and Morales-Espejel,G.E.,The Behaviour of Transverse Roughness in EHL Contacts,Proc.Instn.Mech.Engrs.,part J,J.of Eng.Tribo.,208,pp.121-132,1994.
[12]Ioannides,E.,and Harris,T.A.,A New Fatigue Life Model for Rolling Bearings,Trans.SME,J.of Trib.,107,pp.367-378,1985.
作者:荷兰Nieuwegein的SKF工程研究中心Guillermo Morales Espejel、 Antonio Gabelli和Stathis Ioannides。

