明渠水力设计中的能耗极值假说

黄才安，赵晓冬，周济人

（1.扬州大学水利科学及工程学院，扬州225009；2.南京水利科学研究院河流海岸研究所，南京210024）

明渠水力设计中的能耗极值假说

黄才安1，赵晓冬2，周济人1

（1.扬州大学水利科学及工程学院，扬州225009；2.南京水利科学研究院河流海岸研究所，南京210024）

最小能耗率理论和最大能耗率理论是水力学及河流动力学研究中容易混淆的两种假说。文章从明渠的最优水力断面设计、临界渠道设计、冲积河流河相关系3个方面出发，在理论上证明了能耗极值假说的存在，说明能耗极值假说取最小值和最大值与约束条件、已知条件之间的关系，并将计算结果与现有成果进行了比较。

能量耗散；极值假说；水力学；明渠水流

近年来，不同的极值理论和假设被用来解决流体力学、水力学及河流动力学问题。这些理论和假设常常将一个系统在一定约束条件下的某一个或几个变量，进行极小化或极大化处理。采用极小化方法还是极大化方法，往往在学术上引起混淆，以致于人们对极值假说的有效性产生了怀疑。这些怀疑在很大程度上源于2点：一是对系统本身缺乏严格的定义；二是对优化过程中目标函数和约束条件及已知条件之间的关系缺乏认识。因此有必要进一步研究，澄清其中易混淆的概念。

能耗率极值原理可以叙述为：流体或掺有固体的多相流体，当处在一个独立系统内，在给定的初始和边界条件下流动时，任何时刻的某因变物理量总是这样的分布，使得系统整体的能量耗散率随时为一个极值。将这一原理在不同条件下，用数学形式表达出来，就构成了数学上的极值问题。能耗率极值原理有2种，一是以杨志达、张海燕［1-3］为代表的最小能耗率原理；二是以黄万里［4-5］为代表的最大能耗率原理。

最小能耗率原理将动态平衡与静态平衡相类比，认为对于一个在动力平衡状态下的封闭耗散系统而言，其能量耗散率总是达到最小值，此最小值取决于系统的约束条件。但系统不是处于动力平衡状态时，其能量耗散率就不是最小值，系统将进行自我调节，使得其能量耗散率达到最小，并重新达到平衡。对一般的均匀流输水系统，其最小能耗率原理的数学表达式为

式中：ρ为水的密度；g为重力加速度；Q为流量；J为水力坡度。最小能耗率原理曾被广泛用来研究冲积河流的泥沙运动与河床演变问题。

与最小能耗率原理相对应的是最大能耗率原理。这一原理认为，凡在运动中消散的机械能皆转化为热能，储存在物体里，能量之消散在一定时刻一定温度都使产熵增加，从而使能耗率达到最大。

从实际应用来讲，究竟是取最小值还是最大值，并不影响数学上的求解，因为数学上取得最小或最大值的必要条件都是一样的，对最终结果没有影响。但从理论上来讲，最小值和最大值是2个完全不同的概念，引起混淆将不利于极值假说的发展与运用。

文献［6］以明渠水力学常见问题为例，探讨了最小能耗率原理、最大能耗率原理与优化系统中目标函数、约束条件之间的关系。并对定床明渠水流情况下能耗率极值原理进行了分析，当式（1）流量Q已知，能耗率取极小值；而当式（2）能坡J已知时，能耗率取极大值。本文从一般明渠（含定床与动床水流）的水流方程出发，以矩形断面河槽为例，说明约束条件的不同，对能耗率极值取向的影响，并给出严格的数学证明。

1 明渠能耗极值假说的理论分析

明渠水流的水流连续性方程为

式中：Q为明渠流量；A为过水断面面积；V为断面平均流速。

明渠阻力方程可由Manning公式表示

式中：n为明渠糙率；R为水力半径；J为水力坡度。

结合式（3）和式（4），可得明渠水流方程

1）提防管理范围内，严禁种植根系发达的植物，临大堤较近的范围种植高大乔木，应有隔根措施，防止发达根系破坏大堤的整体性。

对于矩形明渠，设其宽度为b，水深为h，则其宽深比为β=b/h，代入式（5）可得

式（6）为明渠水流的基本方程，也是研究能耗率极值原理的一个目标函数。由于明渠中的流量模数因此式（6）所表示的目标函数的物理意义就是流量模数。由于水深h根据约束条件的不同，目标函数可能取极大或极小值。根据不同的明渠水流特征，水深的约束条件可能与流量Q、能坡J、宽深比β、输沙率Qs等因素有关，一般可表示为

下面分定床明渠、临界渠道、动床渠道等3种情况，分别讨论约束条件与目标函数极值之间的关系。

1.1 定床明渠水力最优断面

明渠水力最优断面的设计是定床水力学中的一个基本问题。对于矩形明渠，其断面面积A与水深h的关系可表述为

式（8）为明渠水力最优断面的设计中的约束条件，代入式（6）得

显然，目标函数X的极值为

即当宽深比βm=2时，X取极值。又

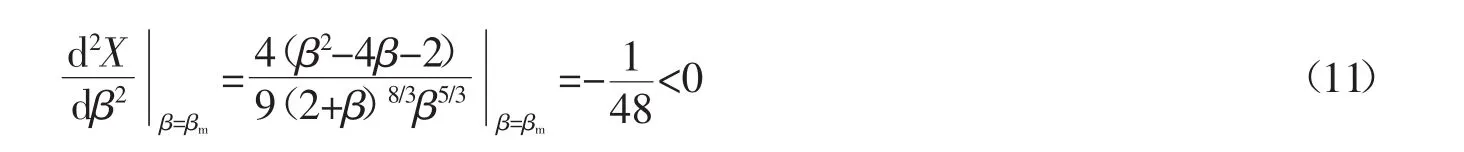
即当宽深比βm=2时，X取极大值。而目标函数X中含3个物理量，即流量Q、能坡J和断面面积A。在明渠糙率n一定时，可以得到以下3点结论：（1）若流量Q和断面面积A已知，则能坡J取极小值；（2）若能坡J和断面面积A已知，则流量Q取极大值；（3）若流量Q和能坡J已知，则断面面积A取极小值。

根据上述分析，3种明渠水力最佳断面定义所得到的结果一致，对于矩形明渠，其宽深比为2，与水力学中的结论完全一致［7］。

1.2 临界渠道

临界渠道（即不冲不淤渠道）设计，此时渠道边界切应力处处等于泥沙起动切应力。为简单起见，假定泥沙起动切应力在边界上是相同的。对矩形明渠而言，其临界渠道的约束条件为

式中:τc为泥沙起动切应力。式（12）可改写为

代入式（6）得

显然，目标函数Y的极值为

即当宽深比βm=2时，Y取极值。又

即当宽深比βm=2时，Y取极小值。由于泥沙起动切应力为已知，则目标函数Y仅是流量Q和能坡J的函数。在明渠糙率n及泥沙起动切应力τc一定，当流量Q为已知时，能坡J取极小值；而当能坡J为已知时，流量Q也为极小值。

说明在临界渠道中无论在何种情况下，能耗率都取极小值。这是与定床明渠水流不同之处。同时得到的临界渠道宽深比仍为2，与明渠水力最佳断面一致。

1.3 动床渠道河相关系

动床稳定渠道即冲淤平衡渠道，有泥沙运动。此时的约束条件是输沙方程，现有很多学者根据不同的物理概念或纯经验，提出了众多输沙方程，仅选择一个有代表性的输沙方程进行分析。这里以Engelund-Hansen公式［8-9］为例，该公式的精度相对较高。

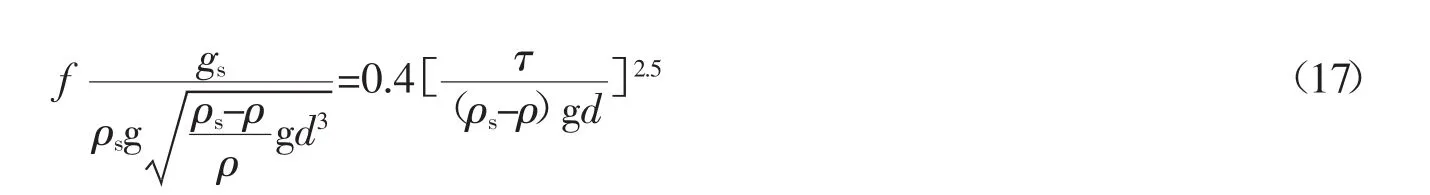
式中：gs为以重量计的单宽床沙质输沙率；ρs为泥沙的密度；d为泥沙中值粒径；f和τ分别为阻力系数和床面切应力，其定义分别为

将式（18）和式（19）代入式（17），可得单宽输沙率gs

将明渠流速公式（4）代入式（20），得到

将单宽输沙率gs乘以明渠宽度b，即为断面输沙率Qs，并考虑宽深比，则

即

其中

将式（23）代入式（6）中，得到目标函数

显然，目标函数Z的极值为

即当宽深比β=46/7时，Z取极值。又

即当宽深比βm=46/7时，Z取极小值。而目标函数Z中包含3个物理量，即流量Q、能坡J和输沙率Qs。在明渠糙率n及泥沙粒径d一定时，可以得到以下3点结论：（1）若流量Q和输沙率Qs已知，则能坡J取极小值；

（2）若流量Q和能坡J已知，则输沙率Qs取极小值；（3）若能坡J和输沙率Qs已知，则流量Q取极大值。

结论（1）就是杨志达、张海燕等提出的最小能耗率［1-3］，结论（2）是White等提出的最大输沙率［10］。而结论（3）是最小能耗率的又一种提法。说明在动床稳定渠道（即河相关系）设计中，能耗率取极小值。而其中得到的宽深比βm=46/7，是根据Engelund-Hansen输沙公式得到的，不同的输沙公式得到的宽深比不同，因此这一宽深比在具体动床稳定渠道设计中仅供参考。上述3个结论在不同的输沙公式时一般均成立。

当采用含有泥沙起动切应力项的输沙公式时，能同时得到临界渠道和动床稳定渠道中的结论。由于其分析过程中的数学推导较为复杂，这里不作介绍。

2 结语

最小能耗率理论和最大能耗率理论是水力学及河流动力学研究中容易混淆的2种假说。本文从明渠水流运动的基本方程出发，对明渠设计中的能耗率极值假说作了进一步研究。从定床最优水力断面设计、临界渠道设计、冲积河流河相关系3个方面，指出能耗率极值假说是取最小值还是最大值与明渠水流的约束条件和已知条件有关，并给出了数学证明。

上述分析仅针对矩形明渠，其结论对其他断面形式的明渠同样适用。

［1］YANG C T，SONG C S.Theory of Minimum Rate of Energy Dissipation［J］.Journal of the Hydraulics Division，1979，105（7）:769-784.

［2］SONG C S，YANG C T.Minimum Stream Power:Theory［J］.Journal of the Hydraulics Division，1980，106（9）:1477-1487.

［3］CHANG H H.Fluvial Processes in River Engineering［M］.New York:Wiley-Interscience，1988.

［4］黄万里.水动力学—热动力学的极值定律［J］.应用数学和力学，1983，4（4）:469-476. HUANG W L.The Extremity Laws of Hydro-Thermodynamics［J］.Applied Mathematics and Mechanics，1983，4（4）:469-476.

［5］黄万里.连续介质动力学最大能量消散定律［J］.清华大学学报，1981，21（1）:87-96. HUANG W L.The Law of Maximum Rate of Energy Dissipation on Continuum Dynamics［J］.Journal of Qinghua University，1981，21（1）:87-96.

［6］黄才安，奚斌.水流能耗率极值原理及其水力学实例［J］.长江科学院院报，2002，19（5）:7-9. HUANG C A，XI B.Study on Extreme Theories of Energy Consumption and Its Hydraulic Examples［J］.Journal of Yangtze River Scientific Research Institute，2002，19（5）:7-9.

［7］吴持恭.水力学［M］.北京:高等教育出版社，1982.

［8］Engelund F，Hansen E.A Monograph on Sediment Transport in Alluvial Streams［M］.Copenhagen:Teknish Forlag，1967:1-62.

［9］黄才安.水流泥沙运动基本规律［M］.北京:海洋出版社，2004.

［10］White W R，Bettess R，Paris E.Analytical Approach to River Regime［J］.Journal of the Hydraulics Division，1982，108（10）:1179-1193.

Extremal hypotheses of energy dissipation used in open channel design

HUANG Cai-an1，ZHAO Xiao-dong2，ZHOU Ji-ren1
（1.College of Hydraulic Science and Engineering，Yangzhou University，Yangzhou 225009，China；2.Department of River and Ocean Engineering，Nanjing Hydraulic Research Institute，Nanjing 210024，China）

In hydraulics and river dynamics studying，there are two confused hypotheses:minimum energy dissipation rate theory and maximum energy dissipation rate theory.From hydraulic efficient cross-section，threshold channel design and hydraulic geometry of alluvial channel in open-channel flow，the existence of extremal value of energy dissipation rate was proved in this paper.Two extremal hypotheses depend on the constraint and given conditions were also proposed.The results were compared with the relating hydraulic theories.

energy dissipation；extremal hypotheses；hydraulics；open-channel flow

TV 133

A

1005-8443（2010）05-0330-05

国家自然科学基金（50779060）

黄才安（1966-），男，江苏省江都人，教授，博士，主要从事水力学及河流动力学方面的研究。

Biography：HUANG Cai-an（1966-），male，professor.