含针片状粗集料的堆砌性能及对混凝土的影响

孙南屏，祁玲

（广东工业大学，广东 广州510090）

1 引言

《建筑用卵石、碎石》GB/T14685-2001规定的粗集料中针片状颗粒含量如下：

表1 粗集料中针片状颗粒含量

经作者实测，粒径在40㎜以下的普通机制碎石中针片状颗粒含量大多在15 %～40%范围，针片状颗粒在粒径小的集料中的含量相对高些，超出表1范围的集料非常多。目前集料资源日益匮乏，充分认识针片状颗粒对集料和混凝土性能的影响，从而按材使用，具有显著的经济和社会效益。

2 双组分体系的理论堆砌问题

堆砌理论[1，2]是描述复合材料增强体或填料之间以何种方式堆砌以及堆砌紧密程度的理论。以有多少种粒径的颗粒参加堆砌来分堆砌体系，可分为单组分体系（单一粒径颗粒参加堆砌），双组分体系（两种粒径颗粒参加堆砌），多组分体系（多于两种粒径颗粒参加堆砌）。用参加堆砌颗粒的形状来描述，堆砌体系主要有双球堆砌体系、纤维堆砌体系以及球-纤维堆砌体系等。

理论密堆砌度λ是描述堆砌体系状态的主要参数，定义为堆砌体系中固体颗粒体积（真实体积）占体系总体积（表观体积）的百分率。λ反映了颗粒堆砌的紧密程度。λ表达式为:

式中 vs—— 颗粒的真实体积；

vb—— 颗粒的表观体积。

单一粒径球体理论密堆砌度为62.5%[2]。

双组分体系的堆砌状况一般用如图1、图2所示的理论堆砌曲线描述。曲线的横坐标代表堆砌体系的颗粒组成，纵坐标代表相对表观密度，定义相对表观体积为体系的表观体积与真实体积的比值，也即λ的倒数。

2.1 双球堆砌体系的理论堆砌曲线[2]

两种粒径球体的理论堆砌曲线见图1。图中参数及线段的含义：

R—— 大球直径与小球直径之比；

C—— 实验测定的大球理论密堆砌体积；M—— 实验测定的小球理论密堆砌体积；

X，Y—— 大球和小球的体积分数，总体积为1。

横坐标（水平轴）代表体系中大、小球混合物的组成。

CA—— 小球加到大球中的浓缩曲线，曲线方程为V=Cx。

MB——大球加到小球中的浓缩曲线，曲线方程为V=x+My。

纵坐标代表相对表观体积（λ的倒数）。相对表观体积理论值在1.0～1.6范围，当体系固体物料的理论密堆砌度为1时，体系堆砌最紧密，无空隙，相对表观体积为1；当体系固体物料达单一粒径球体理论密堆砌度即62.5%，体系堆砌最松散，此时的相对表观体积为1.6。相对表观体积和理论密堆砌度互为倒数。相对表观体积越接近1，颗粒堆砌的紧密程度越高。

图1中的实线表示大小球粒径比R为无穷大时的理论堆砌曲线。当大、小球的直径比为无穷大时，堆砌曲线为两条直线。

图1 双球堆砌体系的理论堆砌曲线

从图1看出：

1)不同粒径的球体掺配可以提高体系的堆砌度，R越大，体系的堆砌度越大；

2)小球加到大球中将较快达到最大密堆砌状态。

2.2 球-纤维体系的理论堆砌曲线[2]

球-纤维的理论堆砌曲线见图2。

图2中参数及线段的含义：

R—— 球直径除以纤维的直径。

S—— 表示50%实体+50%空隙时球的堆砌，相对整体体积等于2.0。

F—— 表示25%实体+75%空隙时纤维的堆砌，相对整体体积等于4.0。

x，y—— 球体和纤维的体积分数，x+y=1。

SE—— 较小直径的纤维加入到较大直径的球中填充空隙时的浓缩曲线，直线方程为V=Sx。

FC—— 大直径的球取代小直径的纤维以及与之相关联的空隙时的浓缩曲线，该直线方程为V=x+Fy。

A—— SE和FC的交点，R值无穷大时，纤维填充球间隙的最大理论密堆砌度。

FD—— 较小直径的球填入到较大直径的纤维之间空隙时的浓缩曲线，直线方程为V=Fy。

SH—— 用粗纤维取代小球及其相关联的空隙时的浓缩曲线，直线方程为V=y+Sx。

B—— FD和SH的交点，为R=0时的最大理论堆砌密度。从图2看出：

1) 球-纤维的混合可以提高体系的堆砌度。球-纤维堆砌体系中出现了点A、B两个最大理论密堆砌度，两者所对应的球-纤维的组成比例不同，但相对表观体积相同。

2) 纤维加到球中将较快达到最大密堆砌状态。

3) 比较图1、图2，尽管双组分体系的颗粒形状不同，但理论堆砌规律相似。

图2 球-纤维体系的理论堆砌曲线

3 针片状颗粒对集料堆砌的影响

针片状颗粒与非针片状颗粒的组合实际上是一种双组分体系的堆砌问题，应该具有上述双组分体系的堆砌规律。

3.1 材料准备

将5～40㎜集料中针片状颗粒手工捡出，然后按质量百分比与非针片状颗粒掺配成针片状颗粒含量分别为0%、15%、30%、45%、60%、100%的混合粗集料备用。

3.2 针片状颗粒含量与粗集料振实表观密度的关系

针片集料含量与粗集料振实表观密度的关系见图3。图3所示的堆砌规律与图1、2相似。

图3 针片集料含量（%）与粗集料振实表观密度的关系

4 针片状颗粒对混凝土性能的影响

4.1 针片状颗粒对混凝土流动性的影响

采用单位质量石子标准稠度需水量（以下称A）来研究，试验方法如下：

1）做水泥标准稠度需水量试验，得W/C。以此W/C拌制水泥浆，测其展开度值，得标准稠度水泥浆的展开度；

2）将水泥、砂以1∶2配比拌合，不断调整水灰比，使砂浆的展开度与（1）中水泥浆的展开度相等，得此时的（W/C）s；

3）以（W/C）s拌和1∶2砂浆，测此砂浆的VB稠度值；

4） 将水泥、砂、石以1∶2∶3.5 [用料量2500∶5000∶8750（g）]配合比拌合，不断调整水灰比，使其VB值与3）中砂浆的VB值相等，得此时的（W/C）h。

单位质量石子标准稠度需水量:

设B为粗集料中针片状颗粒的含量，测定B分别为0%、15%、30%、45%、60%、100%时的A值，研究结果见图4。

图4 针片集料含量（B）与需水量（A）的关系

由图4见，B在30%以内，A小幅减少；B＞30%以后，A迅速增大。B为100%时的A约为B在30%以内A值的两倍。比较图4和图3，两图的变化规律相似。

4.2 针片状集料含量对混凝土成型密实性和强度的影响

研究用32.5矿渣水泥(GB175—2007)，配合比为水泥∶砂∶石=1∶1.55∶3.01，W/C＝0.45，水泥用量为400kg/m3。B分别为0%、15%、30%、45%、60%、100%时混凝土的振实表观密度和100mm×100mm×300mm试件28d抗压强度见图5、6。

5 分析与结论

5.1 分析

对比图3与图1、图2，针片状颗粒与非针片状颗粒的组合符合双组分体系的堆砌规律，与球-纤维体系的理论堆砌规律尤为接近。

与纯纤维一样，100%针片状颗粒的堆砌度很低。适量针片状颗粒加入非针片状颗粒中有明显的提高堆砌度的作用 （图3）。

针片状颗粒含量对堆砌度（图3）、标准稠度需水量（图4）和混凝土的振实表观密度（图5）的影响规律相似。堆砌度高时标准稠度需水量小，混凝土的振实表观密度也大。

针片状颗粒含量超过30%以后混凝土混合料的流动性明显变差（图4），混凝土成型时的密实性即振实表观密度大大下降（图5）。针片状颗粒含量为100%时混凝土与针片状颗粒含量为30%时混凝土的表观密度比为 94.15%，5.85%的变化应主要是孔隙率增大。密实度下降、孔隙率增大也使混凝土强度下降（图6）。可以推论，混凝土的耐久性也随之下降。

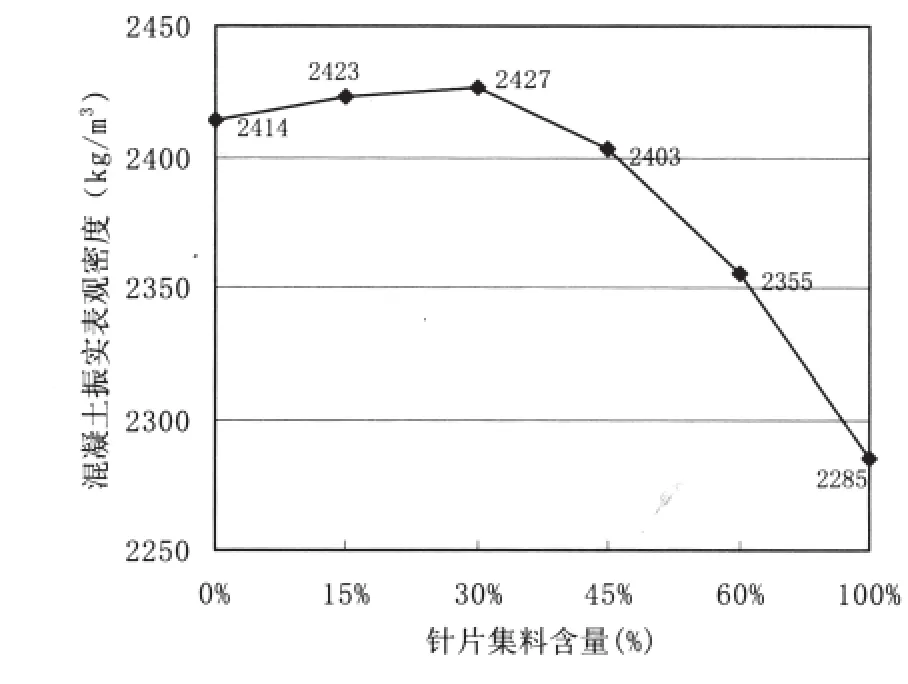
图5 针片集料含量与混凝土振实表观密度的关系

图6 针片集料含量与混凝土抗压强度的关系

实测10～15㎜粒径针片状颗粒760粒/kg，非针片状颗粒590粒/kg；15～20㎜粒径针片状颗粒372粒/kg，非针片状颗粒270粒/kg。加入针片状颗粒会使集料间接触点增多，体系稳定性提高。图4现象说明，针片状颗粒堆砌时有很大的机械咬合力，针片状颗粒超过30%以后集料堆砌结构迅速增强，混凝土的振动液化效果迅速变差。

5.2 结论

1）针片状颗粒与非针片状颗粒的组合符合双组分体系,尤其是球-纤维体系的堆砌规律。适量掺入针片状颗粒，可增大体系的堆砌度。

2）针片状颗粒堆砌时有很大的机械咬合力。机械咬合力会影响混凝土的密实成型，进而影响混凝土的其他性能。

3）从研究结果看，普通混凝土中，增加集料中针片状颗粒的含量至30%不会对混凝土性能有不良影响；在克服成型密实时增大的机械咬合力的前提下，使用针片状颗粒含量30%～40%的粗集料也不会对混凝土性能有明显的影响。

由于集料粒形极其不规则，即使依照标准从集料中逐粒挑选针片状颗粒，结果仍会因人而异。因此，有关针片集料含量的精确数据规定实际操作起来会有偏差。

[1]曾凡，胡永平.矿物加工颗粒学[M].徐州:中国矿业大学出版社，2001.

[2]孙可伟，李如燕.废弃物复合成材技术[M].北京:化学工业出版社，2006.

[3]JGJ 52—2006普通混凝土用砂、石质量及检验方法标准[S].

[4]GB/T14685—2001建筑用卵石、碎石[S].

[5]孙南平，祁玲. 针片状集料对水泥混凝土若干性能的影响[J]. 广西工学院学报,1994(1):16-21.

[6]布然诺夫 (苏).混凝土工艺学 [M].北京:中国建筑工业出版社, 1985.