铁路实际线形测量与计算方法的研究
彭剑秋 刘成龙 彭 攀 刘 林
(西南交通大学土木工程学院, 四川成都 610031)
1 概述
铁路建设不仅指新线建设同时还包括既有线的改建,而既有线的改建就涉及到铁路实际线形的测量,目前通常采用轨检尺结合全站仪的方法得到铁路的相对线形。而铁路实际线形的测量应该包括铁路绝对线形和相对线形的测量,只有这样才能全面评价铁路线路的实际状态和平顺性。铁路线路实际线形的测量与计算,一直是铁路建设和管理的重要问题,也是铁路线路测量技术中倍受关注的问题之一。为了得到既有铁路的实际线形,需要建立全线统一的测量控制网,再在统一的测量控制网中测量线路离散点的坐标。有了铁路线路直线段、圆曲线段和缓和曲线段的离散点坐标,就可以采用最小二乘原理,拟合出铁路线路直线段、圆曲线段和缓和曲线段的实际线形,从而实现整条线路实际线形的测量和拟合计算。下面介绍按照上述思路进行铁路线路实际线形测量和计算的原理。
2 轨道线形测量控制网的建立
轨道线形测量控制网是铁路轨道线形测量的基础,它关系到轨道实际线形测量的方法和精度。目前轨道线形测量控制网普遍采用分级布网的原则布设,一般情况下应分三级布设,分别为CPⅠ、CPⅡ和CPⅢ网。CPⅠ是轨道线形测量的首级平面控制网,点对间距一般为4 000 m左右,测量精度为GPS C级网;CPⅡ是轨道线形测量的二级平面控制网,点间距一般为1 000 m左右,测量精度为GPS D级网或四等附合导线,CPⅡ应附合到CPⅠ上;CPⅢ是轨道线形测量的三级平面控制网,对有砟铁路而言点间距宜在150~200 m之间,测量精度为五等附合导线,CPⅢ应附合到CPⅡ上。CPⅢ控制点宜埋设在路肩上,以方便轨道的线形测量,轨道线形测量控制网宜在轨道线形测量前建网。有砟铁路线形测量三级平面控制网布设如图1所示。
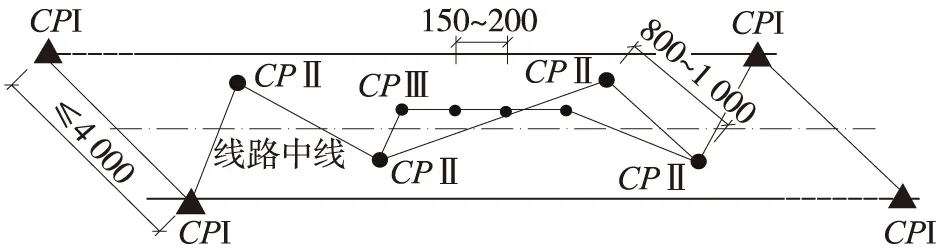
图1 有砟铁路线形测量三级平面控制网示意(单位:m)
3 轨道点坐标的测量及其精度
为了反映既有轨道的实际线形,必须采集既有轨道上特定点的坐标。由于铁路轨道的轨距定义为左右两轨道顶面内侧下方16 mm处的距离,因此既有轨道特定点的坐标,应该是轨道顶面内侧下方16 mm处的坐标。为了测量轨道顶面内侧下方16 mm处的坐标,必须设计制作专用的轨道坐标测量棱镜支架,如图2所示。将专用的轨道坐标测量棱镜支架卡在轨道顶面,则圆棱镜与轨道内侧接触的地方,刚好是轨道顶面内侧下方16 mm处。由于圆棱镜的半径值是固定的已知值,因此只要测量出轨道上多个圆棱镜中心的坐标,就可以反映所测轨道的线形。

图2 轨道坐标测量棱镜支架示意(单位:mm)
轨道点坐标的测量,可以依据轨道线形测量控制网,即在CPⅢ控制点上架设全站仪,用极坐标法测量出轨道上各点的平面坐标。下面分析极坐标法得到的轨道点坐标的测量精度。
由极坐标测量公式可知,轨道上任意一点的坐标xi、yi可以表示为
(1)
式中:XCPⅢ、YCPⅢ为测站点的坐标;S为测站点到棱镜点的水平距离;A为设站点到后视点的坐标方位角;α为测站上测量得到的后视与前视方向间的夹角。
由式(1)微分并整理得
(2)
式中,ρ=206 265″。由误差传播定律可知,轨道点xi、yi,坐标的中误差mxi、myi可以表示为
(3)

若不顾及CPⅢ控制点的点位误差、后视方位角的中误差、仪器对中和整平误差,式(3)可以表示为
(4)
则实测轨道点的点位中误差为
(5)
结合式(4)、式(5),当A+α=45°或135°时,sin2(A+α)=cos2(A+α),此时mxi=myi。
若以测角标称精度为2″、测距标称精度为2 mm+2×10-6D的普通全站仪测量轨道点坐标,同时考虑到CPⅢ控制点的点间距最大为200 m,把上述有关数据带入式(4)、式(5),可计算出轨道点点位中误差最大为±3.09 mm。
通过上面分析和精度估算可知,在CPⅢ控制点上设站,采用全站仪极坐标法测量铁路轨道坐标实际上是可行的,而且测量精度较高,为铁路的实际线形计算打下了良好的基础。
4 轨道实际线形的计算原理
任意一条铁路都是由直线、圆曲线、缓和曲线三种线元构成的,三种线元都可以视为不完整缓和曲线的特例。轨道实际线形的计算,就是采用上面介绍的方法,在线路坐标系下采集轨道某一线元上若干离散点的坐标,然后通过采集到的若干测量点坐标,拟合出该线元的线形,以及整条线路的线形。
下面将逐一介绍直线、圆曲线和缓和曲线三种线元线形拟合计算的数学模型。
4.1 直线线形拟合计算的数学模型
铁路线路中最简单的线元为直线,直线的线形拟合可按以下方法进行。由直线线元上采集得到的轨道点坐标以及数学公式可知,直线线元上某一点的误差方程可写为
yi=kxi+b+vi(i=1,2,…,n)
(6)
或
vi=yi-(kxi+b) (i=1,2,…,n)
(7)
由于直线线元上各点的观测方程是按误差方程的形式开列的,因此应采用间接平差的方法求出直线线元的拟合系数。由直线线元上采集的各点坐标及其误差方程,可组成间接平差误差方程的矩阵形式为

(8)
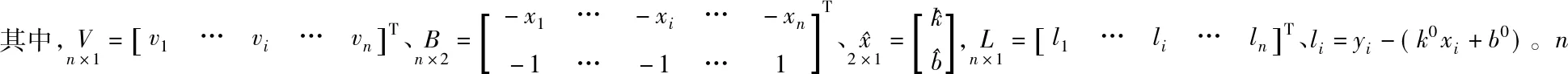
按最小二乘法原理[3],可得法方程为
(9)
式中,N=BTB,其秩为R(N)=R(B)=t,亦即N非奇异,存在凯利逆N-1,所以法方程的解唯一为
(10)
那么,待求直线线元参数的最优解为
(11)
4.2 圆曲线线形拟合计算的数学模型
铁路线路需要转变方向时,最主要的曲线线元是圆曲线,下面介绍圆曲线线形的拟合方法。由数学公式可知,圆曲线上任一点圆的标准方程为
(x-XO)2+(y-YO)2=R2
(12)
其中,(XO,YO)为圆心O的坐标;R为圆曲线的设计半径。
长期的自我封闭,让留守儿童厌恶与人交往,出现问题都藏在心底,不愿意参加集体活动,导致性格孤僻冷淡。从家庭的角度分析,只有强化父母的法定监护责任,完善监护制度,减少父母对孩子的无形伤害,才能切实保护留守儿童的身心健康发展。
圆曲线上第i个测量点p(xi,yi)i∈(1,2,…n)到圆心的距离为
(13)
则Ri与R的差值为di=Ri-R,也即
[(xi-Xo)2+(yi-Yo)2]-R2=
(Ri+R)(Ri-R)=(Ri+R)di≈2Rdi
(14)
将上式整理后得
(15)
令上式中
上式中R0为圆曲线半径R的近似值,则式(15)为
di=axi+byi+c-li
(16)
由圆曲线线元上测量的各点坐标及其上式,可组成圆曲线线形拟合计算误差方程的矩阵形式(见式(8))。
根据最小二乘法原理和式(8),可求解出a、b、c;因而,可进一步求解出半径R与圆心O的坐标(XO,YO)
(17)
4.3 缓和曲线线形拟合计算的数学模型
铁路线路在直线和圆曲线之间,一般要加设缓和曲线。我国铁路缓和曲线采用的参数方程为[1]
(18)
其中:xi、yi为缓和曲线上任意点i在以直缓点为坐标原点、以直缓点的切线方向为x轴和与x轴相垂直且方向指向曲线内侧为y轴的局部坐标系中的坐标,li为该点到直缓点的缓和曲线长,l0为缓和曲线的全长。
根据参考文献[1]以及有关数学知识,缓和曲线上任一点i在局部坐标系下的坐标yi,也可以表示为
(19)
其中,Xi、Yi为缓和曲线上第i点在线路坐标系下的坐标,k、b为线路坐标系下过直缓点切线的斜率与切距。由式(19)可知,在获得缓和曲线上任一点的线路坐标和过直缓点切线的斜率以及切距的情况下,就可以知道该点在局部坐标系中的坐标yi。
根据式(18)中的第二式,缓和曲线上任一点i以及该点的下一点(i+1)的y坐标[1],还可以表示为
(20)

为开列误差方程以及运用最小二乘拟合出缓和曲线的最佳线形,可将式(20)中的两式整理为
(21)
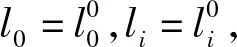
(22)
将缓和曲线上采集的各点坐标及其曲线长近似值代入上式,就可组成缓和曲线线形拟合误差方程的矩阵形式(见式(8))。
按最小二乘法原理,可得缓和曲线长的最优解为
按照上述方法测量和计算出铁路线路直线、圆曲线和缓和曲线三个线元的线形,就可以得到整条线路的实际线形。
5 应用实例
基于上述铁路实际线形的测量和计算原理,采用visual C#2003计算机语言编制了铁路线路线形拟合计算程序。该程序在读取线路上测量点的坐标数据后,能够计算出铁路线路实际线形的要素,包括圆曲线的半径、缓和曲线长度、切线长、曲线长、外矢距、切曲差以及五大桩的坐标等。
为验证本文所提出的铁路实际线形计算方法的正确性,选取某段铁路的设计线形并绘制在AUTOCAD上,然后提取该设计线形上的直线、缓和曲线和圆曲线上的离散点坐标,输入到本文研制的铁路线路拟合计算程序中,计算该段线路的圆曲线的半径、缓和曲线长度、切线长、曲线长、外矢距、切曲差以及五大桩的坐标等线形参数,发现拟合计算的线形参数与设计的线形参数完全相等,由此证明本文提出的线形拟合计算模型在理论上是正确和严密的,所研制程序的计算结果也是正确的。
6 结论
(1)本文提出了一种铁路轨道实际线形控制测量及其离散点坐标测量的思路和方法,理论分析表明该方法在目前具有较强的操作性,测量精度能够满足轨道线形测量和分析的要求,可以在铁路轨道实际线形测量中推广应用。
(2)利用在轨道上直接测量得到的离散点坐标,分别提出了轨道直线、圆曲线以及缓和曲线线形拟合计算的数学模型。理论分析和实验计算结果表明,这些数学模型能够拟合出铁路常见直线和曲线的线形,可用于既有铁路实际线形测量和新建铁路竣工线形测量的线形拟合计算。
[1]王兆祥.铁道工程测量[M].北京:中国铁道出版社,2003:228-233.
[2]吴耀庭.铁路曲线及其养护[M].北京:中国铁道出版社,2001:47-48
[3]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社,2003:102-104
[4]张正禄.工程测量学[M].武汉:武汉大学出版社,2005:163-169
[5]彭壮志,虞欣.一种多圆目标的联合检测方法[J].测绘科技情报,2007(4):3-7
[6]铁建设[2006]189号 客运专线无砟轨道铁路工程测量暂行规定[S]

