基于杠杆效应SV模型和EGARCH模型VaR的比较

赵世海 ,汤志明

(1.重庆大学 工商管理学院，重庆 400030；2.重庆市人民防空办公室，重庆 400010）

0 引言

当前,金融市场风险成为全球金融机构及监管当局关注的焦点。与之对应，风险测量技术也在近年得到了发展。其中，VaR由于其明确的经济含义及易操作性成为金融市场风险测量的主流模型。

最基本的分析方法是将市场因子看成是具有固定方差的正态分布从而简单估计VaR。由于金融市场的时变性，这样得出的结果显然太过粗糙，寻找一种最能刻画市场因子回报波动性的模型至关重要。加权正态模型(WTN)考虑到了波动动态时变性,但权值赋予依赖于经验,缺乏理论支持。近年来,异方差模型被认为是最能刻画金融市场波动性的模型，GARCH模型族被广泛应用于VaR值的计算，其中EGARCH模型被认为能较理想测量VaR。然而，GARCH模型族面对金融时间序列“高峰厚尾”、杠杆效应、平方序列微弱而持久的自相关性等显著特征也显得十分脆弱,国外已有大量实证研究指出了这些问题。SV模型是另一类异方差模型，具有数理金融学和金融计量经济学双重根源，其最显著特征是将随机过程引入到方差表达式中，被认为是刻画金融市场波动性的最理想模型。Harvey A、Kim等学者做过大量关于SV模型族与GARCH族模型的比较研究，认为SV模型所刻画的波动性与金融市场特征更加吻合。尽管SV模型功能强大,但由于其参数估计困难，直到近年才开始得到运用，而基于杠杆效应SV模型下VaR值的计算及其与基于EGARCH模型下VaR值的比较，国内外文献很少。

本文旨在利用杠杆效应异方差模型来测量股市的VaR值。从模型出发说明了杠杆效应SV模型具有比EGARCH模型更与金融市场实际特征相吻合的数值指标。分别得出了基于两种模型下的上海股市的VaR值,实证研究说明利用具有杠杆效应SV模型计算出的VaR值更好地反映了上海股市的风险水平。本文对两种异方差模型进行比较,并从动态角度考虑VaRt时间序列的特征。

1 Va R的计算

在值风险VaR（Value-at-Risk）由于其测量的综合性，目前已成为证券市场风险测量的主流方法。它的定义可表述为“在一定置信度下将来一定持有期内的最大损失”。也即是在将来的某个时期，有1-α的可能性下，最大的损失值。即

P{Rt＞-VɑRt}=1-α

其中:Rt为资产在第t期的收益；α为显著性水平;VɑRt为t时刻α水平下的VaR，取值为正。

通常情况下，一般的异方差模型均认为各时点上收益服从具有时变方差的条件正态分布,所以：

Rt|It-1～N(μt,σ2)（It–1代表过去的信息集）

因此

即当收益的条件分布为正态时,VɑRt是σt的线性函数。近年来理论和实证研究都说明时间序列的非正态性有着其异方差根源,所以选用当前处理异方差领域的工具——EGARCH和基于杠杆效应SV模型来刻画股市收益的波动性,并进行比较,进而获得较精确的VaR值。

2 EGARCH和杠杆效应SV模型对波动值的计算

2.1 EGARCH模型

EGARCH模型表述为：

其中p、q由AIC信息和SCI信息确定，在一般情况下，取EGARCH（1，1）模型。本文假设rt服从期望为μ，方差为σ2的正态分布。利用实际数据,估计出EGARCH(1,1)中的参数θ、ψ、γ后,直接利用式递推计算出各个时间的波动值，只是要注意消除初始值ε0，σ0的影响。

2.2 杠杆效应的SV模型

一般的SV模型表述为：

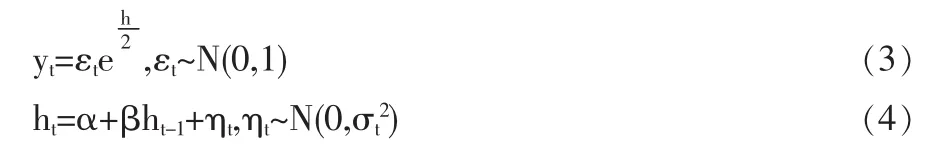
其中，yt是在t日的收益，ht表示t日的对数波动。假定ht服从一个一阶自回归过程，是不可观测的，对数波动的持续性用参数β表示。基本SV 模型中假设εt、ηt是两个相互独立的误差过程，因此没有考虑到前面提到的所谓的“杠杆效应”。如果令(3) 和(4) 中的误差项 εt、ηt相关(严格地说是负相关)，SV 模型就能捕捉到股票市场中的“杠杆效应”。“杠杆效应”在股票收益中表现得比较明显，而在汇率市场中则要差些。在基本SV 模型中引入εt、ηt的相关系数ρ，就可以得到具有杠杆效应的SV模型：

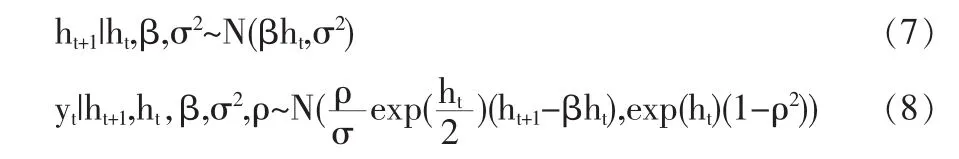
对SV模型的估计，本文选同使用BUGS软件，用马尔科夫链蒙特卡洛（MCMC）方法进行模型参数估计。

3 实证研究——测定深证指数的Va R

3.1 样本数据的选取时段的选择

本文根据研究的需要，同时依据中国股票市场的性质，以及股市发展的代表情况，选取上证指数和深证综指。在样本时段的选择上，根据中国股票市场发展的政策进行选取，我们选取1999年1月1日到2007年12月30日的数据，数据来源为香港理工大学中国会计与金融研究中心和深圳市国泰安信息技术有限公司联合开发的“中国股票研究市场交易数据库”。数据处理与分析采用软件为Eviews5.0。

表1 各股指的基本统计特征（1997-1-1～2005-12-30）

3.2 数据的基本分析

收益率采用JP摩根集团的对数收益率的概：R（t）=ln(Pt)-ln(Pt-1)=ln(Pt/Pt-1)。通过我们计算的2170个收益率数据，考察该收益序列的统计特征：

（1）各股指的基本统计特征。

根据表1所得的各股票指数对数收益的偏度、峰度以及J-B检测值可知,深证指数不符合正态分布，利用QQ图也可进一步得知,深证指数收益存在着明显的尖峰、厚尾特征。

（2）模型的估计结果

用 BUGS软件MCMC方法对 SV模型进行了估计,对GARCH(1,1)的估计采用一般的极大似然法,利用Matlab编写计算机程序：

表2 深证指数EGARCH模型的参数估计结果

从表2、表3可以看出，EGARCH模型和SV模型都能刻画深证指数的杠杆效应。

3.3 VaR值计算及其准确性检验

分别用EGARCH模型和SV模型计算出的{σt2}序列及其表1中的平均值代入方程（0），分别计算得出在置信度1%，2%，3%，4%，5%VaR 值。

VaR是一个估计量，其效果要通过检验，通常的方法是通过失败率来检验，即:记录实际发生的损失，然后计算超过VaR的次数(或天数)比例是否大于设定的置信度。库皮克[8]给出了这种检验方法。其方法是构造一个LR统计量，将投资组合观察的实际每日盈亏结果与测定的VaR值进行比较，如果VaR模型测定的VaR 是准确的，那么，投资组合实际亏损超过测定VaR值的例外情形可被视为从一个二项分布中出现的独立事件，即如果实际亏损幅度在测定VaR值以内，则被视为一个成功的事件(为1)，如果实际亏损幅度在测定的VaR 值以上，则被视为一个失败事件(为0)。因此,失败事件出现的概率应为预定的失效水平。

假定计算VaR 的置信度为α，实际考察天数为T,失败天数为N,则失败频率为p(=N/T),失败的期望概率为p*(=1-α)。零假设为p=p*，这样对VaR 模型准确性的评估就转化为检验失败频率p是否显著不同于p*。Kupiec[6]提出了零假设的似然比率检验:

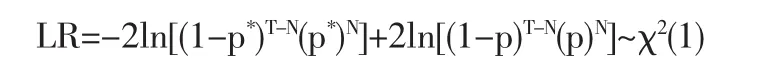
在零假设条件下，统计量LR服从自由度为1的χ2分布。本文计算了α分别等于1% 、2%、3% 、4%和5%下的失败率，似然比p值及实际失败率与α的相对误差。

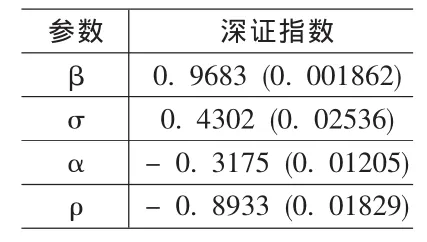
表3 深证指数杠杆效应SV模型的参数估计结果

表4 深证指数收益率 VaR失败率及似然比p值

3.4 数据分析及结论

迄今为止，SV模型被认为是对异方差最精确的估计模型，本文通过对SV与GARCH 两个模型的对比说明，利用SV模型得出的方差序列可以认为是对股市波动性最准确的反映。为了对比讨 论基于两种模型下VaR对风险测度的准确性，从表4可以看出，深证指数不同置信度 (1-α)下EGATCH得到的VaR与分位数α普偏存在正的相对误差，越在尾部越突出，表明它们存在低估风险，捕捉厚尾能力较差，而基于杠杆效应SV模型则存在负误差。基于EGARCH和杠杆效应的SV模型都没有出现被拒绝的情况，他们都有较高的p值。

4 结束语

本文讨论了如何利用GARCH和SV模型计算VaR值,并通过实证分析得知，基于SV模型下的VaR值更具有动态性、准确性,但是还存在几个问题有待完善。

(1)仅研究了基本市场因子回报的简单的VaR值的测度，而实际中遇到的常是一些多个资产组合潜在损失的问题。如何利用SV模型测定包含多个市场因子波动性，并寻求适当的资产定价公式，计算具体资产的风险是需要进一步讨论的问题。

(2)所采取的标准SV模型虽然较其他的异方差模型更能刻画“厚尾”现象，但其对随机项的条件正态假设，仍使其难以对实际数据做更好的概括,所以应探索扩展SV模型。一般认为，对金融序列“高峰厚尾”性质的刻画，SV-t和SV-GED模型要比SV-正态更有效。

[1]Morgen J P.Risk Metrics-Technical Document[M].New York:Morgen Trust Company Global Research,1995.

[2]Billo M,Pelizzon L.Value-at- risk:A Multivariate Switching Regime Approach[J].Journal of Empirical Finance,2000,7.

[3]Vlaar P J G.Value at Risk Models for Dutch Bone Portfolios[J].Journal of Banking and Finance,2000,24.

[4]Beltratti A,Morana C.Computing value at Risk with High Frequency Data[J].Journal of Empirical Finance,1999,(6).

[5]Joans Andresson.On the Normal Inverses Gaussian Stochastic Volatility Model[J].Journal of Bussiness of Economics Statistics,2001,19.

[6]Harvey A C,Ruiz E,Shephard N.Multivariate Stochastic Variance Models[J].Reviewof Economic Studies,1994,61.

[7]Kim Shephard,Chib.Stochastic Volatility:Likelihood Inference and Comparison with ARCH Models[J].Review of Economic Studies,1998,65.

[8]李汉东,张世英.随机波动模型的持续性和协同持续性研究[J].系统工程学报,2002,17(4).